Month: December 2015

Prime years and such

On By rolcottIn General: Fun Stuff, Uncategorized3 Comments

I’ve liked 4s and 6s ever since when, but lately 3s and 7s have been cropping up.  A lot.  And they have a really weird connection with 2016.

For me New Year has always been an opportunity to inspect the upcoming year’s number for interesting properties.

Maybe the easiest way for a number to be interesting is to be prime, that is, not divisible by anything other than itself and one.  My Uncle Harold once proved to me that all odd numbers are prime.

“One’s a prime, and so are three and five.  How about seven?  Seven’s prime.  Nine?  Not a prime but we can throw that one out as experimental error.  Eleven?  Prime.  Thirteen?  Prime.  Case closed.”

They use that logic a lot in politics nowadays.

There are a few prime-ity tests that just need a quick glance.  Take 2015 for example.  Ends with a “5” so it’s got to be divisible by five.  Not a prime.  A number ending with a “0” is like ending with twice five so it’s not prime either.

Take 2016.  Ends in an even digit so it’s divisible by two.  Not a prime.  Moreover, it fails the “nines test” — add up all the digits (2+0+1+6=9).  If the total is nine or divisible by nine then the number itself is divisible by nine (and by three) so it’s non-prime.  2016 is also divisible by seven but that’s not as easy to diagnose.

That’s about it for quickies.  Beyond those tests you have to slog through dividing the target by every prime number from three up to the target’s square root.  Why stop there?  Because any factor bigger than the square root will have a partner smaller than the square root.

Remember Party Like It’s 1999 (prime)?  Very popular when the Artist Then Known As Prince produced it in 1982 (not a prime).  Unfortunately, we who were working on Y2K projects were too busy to party that year so we couldn’t celebrate 1999 being prime until it was all over.

Y2K itself, 2000, definitely wasn’t prime.  If you know that 1999 is prime you know 2000 can’t be because after you get past 1-2-3, no two adjacent numbers can be prime — one of them would have to be even.  Next-but-one can work, though: both 1997 and 1999 are prime.  Primes separated by two like that are twin primes.

If 2016 won’t be a prime year, is there another way it can be special?  Hmmm…  2016 isn’t a perfect square, nor is it the sum of two squares.  Neither its square nor its cube are particularly noteworthy, but the square PLUS the cube is kinda cute: their sum is 8,197,604,352 which contains every digit just once.

According to The On-Line Encyclopedia of Integer Sequences, 2016 is a hexagonal number.  Start with a dot.  Make that dot one corner of a hexagon of dots.  Then add a hexagon around that, one more dot per side,  keeping the original dot as a corner (like the plan for a starter motte-and-bailey castle)…Hexagonal numbers Keep going until the outermost hexagon has 32 dots along each edge.  All the hexagons together will have exactly 2016 dots.

The OEIS says that 2016 is a participant in at least 925 more special sequences, so I guess it’s a pretty cool number after all.

Those 3s and 7s?  Here they come….

My nominee for Puzzle King of The World is my good friend Jimmy.  I challenged him once to find the connection between

  • the British Army’s WWII section number (2701) for Alan Turing’s super-secret cryptography unit at Bletchley Park, and
  • Jean Valjean’s prisoner number (24601) in Les Misérables 

Turns out it’s all about the primes.  2701 is the product of two primes: 73×37.  24601 is also the product of two primes 73×337.   Better yet, both of the product expressions are palindromes in their digits (7337, 73337). To put whipped cream on top, I first noticed the connection during my 73rd year.

So then of course I went looking for other 3…7 and 7…3 primes. There aren’t a lot of them. Going all the way out to 1037 I found:

37 73
337 733
 (3,337 is 47×71, not a prime) 7,333
333,337 733,333

Pretty good symmetry there.

OK, back to number 2016. I asked Mathematica®, “How many different pairs of primes, like 1999 and 17, sum to 2016?”

What do you suppose the answer was?  Yup, “73.”

Oh, and the next prime year is 2017.  It’ll be great.

~~ Rich Olcott

The direction Newton avoided facing

On By rolcottIn Physics: Fundamentals, Physics: Newton and Gravity, UncategorizedLeave a comment

Reading Newton’s Philosophiæ Naturalis Principia Mathematica is less challenging than listening to Vogon poetry.  You just have to get your head working like a 17th Century genius who had just invented Calculus and who would have deep-fried his right arm in rancid skunk oil before he’d admit to using any of his rival Liebniz’ math notations or techniques.

Newton II-II ellipseNewton was essentially a geometer. These illustrations (from Book 1 of the Principia) will give you an idea of his style.  He’d set himself a problem then solve it by constructing sometimes elaborate diagrams by which he could prove that certain components were equal or in strict proportion.

Newton XII-VII hyperbolaFor instance, in the first diagram (Proposition II, Theorem II), we see an initial glimpse of his technique of successive approximation.  He defines a sequence of triangles which as they proliferate get closer and closer to the curve he wants to characterize.

The lines and trig functions escalate in the second diagram (Prop XII, Problem VII), where he calculates the force  on a body traveling along a hyperbola.

Newton XLIV-XIV precessionThe third diagram is particularly relevant to the point I’ll finally get to when I get around to it.  In Prop XLIV, Theorem XIV he demonstrates something weird.  Suppose two objects A and B are orbiting around attractive center C, but B is moving twice as fast as A.  If C exerts an additional force on B that is inversely dependent on the cube of the B-C distance, then A‘s orbit will be a perfect circle (yawn) but B‘s will be an ellipse that rotates around C, even though no external force pushes it laterally.

In modern-day math we’d write the additional force as F∼(1/rBC3), but Newton verbalized it as “in a triplicate ratio of their common altitudes inversely.”  See what I mean about Vogon poetry?

Now, about that point I was going to get to.  It’s C, in the center of that circle.  If the force is proportional to 1/r3, what happens when r approaches zero?  BLOOIE, the force becomes infinite.

In the previous post we used geometry to understand the optical singularity at the center of the Christmas ball.  I said there that my modeling project showed me a deeper reason for a BLOOIE.  That reason showed up partway through the calculation for the angle between the axis and the ring of reflected  light.  A certain ratio came out to be (1-x)/2x, where x is proportional to the distance between the LED and the ball’s center.  Same problem: as the LED approaches the center, x approaches zero and BLOOIE.  (No problem when x is one, because the ratio is 0/2 which is zero which is OK.)

Singularities happen when the formula for something goes to infinity.

Now, Newton recognized that his central-force (1/rn)-type equations covered gravity and magnetism and even the inward force on the rim of a rotating wheel.  It’s surprising that he didn’t seem too worried about BLOOIE.

I think he had two excuses.  First, he was limited by his graphical methodology.  In most of his constructions, when a certain distance goes to zero there’s a general catastrophe — rectangles and triangles collapse to lines or even points, radii whirl aimlessly without a vertex to aim at…  His lovely derivations devolve into meaninglessness.  Further advances would depend on the  algebraic approach to Calculus taken by the detested Liebniz.

Second (here’s the hook for this post’s title), Newton was looking outward, not inward.  He was considering the orbits of planets and other sizable objects.  r is always the distance between object centers.  For sizable objects you don’t have to worry about r=0 because “center-to-center equals zero” never occurs.  If the Moon (radius 1080 miles) were to drop down to touch the Earth (radius 3960 miles), their centers would still be 5000 miles apart.  No BLOOIE.

Actually, there would be CRUMBLE instead of BLOOIE because a different physical model would apply — but that’s a tale for another post.

The moral of the story is this.  Mathematical models don’t care about infinities, but Nature does.  Any conditions where the math predicts an infinite value (for instance, where a denominator can become zero) are prime territory for new models that make better predictions.

~~ Rich Olcott

Circular Logic

On By rolcottIn General: Fun Stuff, Mathematics, Uncategorized2 Comments

We often read “singularity” and “black hole” in the same pop-science article.  But singularities are a lot more common and closer to us than you might think. That shiny ball hanging on the Christmas tree over there, for instance.  I wondered what it might look like from the inside.  I got a surprise when I built a mathematical model of it.

To get something I could model, I chose a simple case.  (Physicists love to do that.  Einstein said, “You should make things as simple as possible, but no simpler.”)

I imagined that somehow I was inside the ball and that I had suspended a tiny LED somewhere along the axis opposite me.  Here’s a sketch of a vertical slice through the ball, and let’s begin on the left half of the diagram…Mirror ball sketch

I’m up there near the top, taking a picture with my phone.

To start with, we’ll put the LED (that yellow disk) at position A on the line running from top to bottom through the ball.  The blue lines trace the light path from the LED to me within this slice.

The inside of the ball is a mirror.  Whether flat or curved, the rule for every mirror is “The angle of reflection equals the angle of incidence.”  That’s how fun-house mirrors work.  You can see that the two solid blue lines form equal angles with the line tangent to the ball.  There’s no other point on this half-circle where the A-to-me route meets that equal-angle condition.  That’s why the blue line is the only path the light can take.  I’d see only one point of yellow light in that slice.

But the ball has a circular cross-section, like the Earth.  There’s a slice and a blue path for every longitude, all 360o of them and lots more in between.  Every slice shows me one point of yellow light, all at the same height.  The points all join together as a complete ring of light partway down the ball.  I’ve labeled it the “A-ring.”

Now imagine the ball moving upward to position B.  The equal-angles rule still holds, which puts the image of B in the mirror further down in the ball.  That’s shown by the red-lined light path and the labeled B-ring.

So far, so good — as the LED moves upward, I see a ring of decreasing size.  The surprise comes when the LED reaches C, the center of the ball.  On the basis of past behavior, I’d expect just a point of light at the very bottom of the ball (where it’d be on the other side of the LED and therefore hidden from me).

Nup, doesn’t happen.  Here’s the simulation.  The small yellow disk is the LED, the ring is the LED’s reflected image, the inset green circle shows the position of the LED (yellow) and the camera (black), and that’s me in the background, taking the picture…g6z

The entire surface suddenly fills with light — BLOOIE! — when the LED is exactly at the ball’s center.  Why does that happen?  Scroll back up and look at the right-hand half of the diagram.  When the ball is exactly at C, every outgoing ray of light in any direction bounces directly back where it came from.  And keeps on going, and going and going.  That weird display can only happen exactly at the center, the ball’s optical singularity, that special point where behavior is drastically different from what you’d expect as you approach it.

So that’s using geometry to identify a singularity.  When I built the model* that generated the video I had to do some fun algebra and trig.  In the process I encountered a deeper and more general way to identify singularities.

<Hint> Which direction did Newton avoid facing?

* – By the way, here’s a shout-out to Mathematica®, the Wolfram Research company’s software package that I used to build the model and create the video.  The product is huge and loaded with mysterious special-purpose tools, pretty much like one of those monster pocket knives you can’t really fit into a pocket.  But like that contraption, this software lets you do amazing things once you figure out how.

~~ Rich Olcott

And now for some completely different dimensions

On By rolcottIn Mathematics: Dimensions, Physics: Fundamentals, UncategorizedLeave a comment

Terry Pratchett wrote that Knowledge = Power = Energy = Matter = Mass.  Physicists don’t agree because the units don’t match up.

Physicists check equations with a powerful technique called “Dimensional Analysis,” but it’s only theoretically related to the “travel in space and time” kinds of dimension we discussed earlier.

Place setting LMTIt all started with Newton’s mechanics, his study of how objects affect the motion of other objects.  His vocabulary list included words like force, momentum, velocity, acceleration, mass, …, all concepts that seem familiar to us but which Newton either originated or fundamentally re-defined. As time went on, other thinkers added more terms like power, energy and action.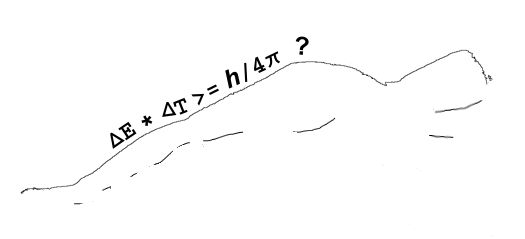

They’re all linked mathematically by various equations, but also by three fundamental dimensions: length (L), time (T) and mass (M). (There are a few others, like electric charge and temperature, that apply to problems outside of mechanics proper.)

Velocity, for example.  (Strictly speaking, velocity is speed in a particular direction but here we’re just concerned with its magnitude.)   You can measure it in miles per hour or millimeters per second or parsecs per millennium — in each case it’s length per time.  Velocity’s dimension expression is L/T no matter what units you use.

Momentum is the product of mass and velocity.  A 6,000-lb Escalade SUV doing 60 miles an hour has twice the momentum of a 3,000-lb compact car traveling at the same speed.  (Insurance companies are well aware of that fact and charge accordingly.)  In terms of dimensions, momentum is M*(L/T) = ML/T.

Acceleration is how rapidly velocity changes — a car clocked at “zero to 60 in 6 seconds” accelerated an average of 10 miles per hour per second.  Time’s in the denominator twice (who cares what the units are?), so the dimensional expression for acceleration is L/T2.

Physicists and chemists and engineers pay attention to these dimensional expressions because they have to match up across an equal sign.  Everyone knows Einstein’s equation, E = mc2. The c is the velocity of light.  As a velocity its dimension expression is L/T.  Therefore, the expression for energy must be M*(L/T)2 = ML2/T2.  See how easy?

Now things get more interesting.  Newton’s original Second Law calculated force on an object by how rapidly its momentum changed: (ML/T)/T.  Later on (possibly influenced by his feud with Liebniz about who invented calculus), he changed that to mass times acceleration M*(L/T2).  Conceptually they’re different but dimensionally they’re identical — both expressions for force work out to ML/T2.

Something seductively similar seems to apply to Heisenberg’s Area.  As we’ve seen, it’s the product of uncertainties in position (L) and momentum (ML/T) so the Area’s dimension expression works out to L*(ML/T) = ML2/T.

SeductiveThere is another way to get the same dimension expression but things aren’t not as nice there as they look at first glance.  Action is given by the amount of energy expended in a given time interval, times the length of that interval.  If you take the product of energy and time the dimensions work out as (ML2/T2)*T = ML2/T, just like Heisenberg’s Area.

It’s so tempting to think that energy and time negotiate precision like position and momentum do.  But they don’t.  In quantum mechanics, time is a driver, not a result.  If you tell me when an event happens (the t-coordinate), I can maybe calculate its energy and such.  But if you tell me the energy, I can’t give you a time when it’ll happen.  The situation reminds me of geologists trying to predict an earthquake.  They’ve got lots of statistics on tremor size distribution and can even give you average time between tremors of a certain size, but when will the next one hit?  Lord only knows.

File the detailed reasoning under “Arcane” — in technicalese, there are operators for position, momentum and energy but there’s no operator for time.  If you’re curious, John Baez’s paper has all the details.  Be warned, it contains equations!

Trust me — if you’ve spent a couple of days going through a long derivation, totting up the dimensions on either side of equations along the way is a great technique for reassuring yourself that you probably didn’t do something stupid back at hour 14.  Or maybe to detect that you did.

~~ Rich Olcott