Category: General: Fun Stuff

Fibonacci’s Legacy

On By rolcottIn General: Fun Stuff, Mathematics, Mathematics: Logs and Exponentials, Uncategorized3 Comments

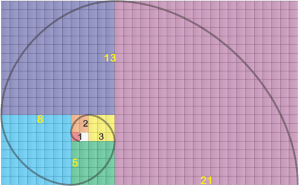
Of course you’ve seen images featuring the Fibonacci spiral, maybe one that overlays the spiral onto a snail shell or the whorls of a sunflower head. As you see, it’s derived from a series of squares, the side of each equal to the sum of the sides of the next two smaller ones. The spiral smoothly connects opposite corners of successive squares. Fibonacci didn’t invent the spiral, but he did discover the {1, 1, 2, 3, 5, 8, 13, 21, 34, …} series it exploits. He’s famous for the series, but that was as dust before his other major contribution to our world.

Leonardo was the foremost mathematician of 13th‑century Italy. His father was Guglielmo Bonacci so Leonardo was figli di (son of) Bonacci, hence fi’Bonacci or Fibonacci. As a citizen of the Pisan Republic he was often cited as Leonardo di Pisa, preceding the more famous Leonardo of Vinci (a district in Florence, 90 kilometers east of Pisa) by nearly three centuries.

In 1202 Fibonacci wrote a ground‑breaking mathematics textbook, Liber Abaci, that included many solved examples of problems from trade and finance. His famous rabbit problem was part of the mix.

Fibonaci’s rabbits, diagram by “Romain” under CCS-A 4.0 license

Suppose you’ve got a pair of immortal rabbits that multiply like clockwork — each pair more than a month old produces one additional pair per month. How many pairs would you have after n months? The figure shows the first few stages of the process. At the end of any month you’ve got all the start‑of‑month rabbits plus one pair for each new pair that reached one‑month maturity. 1+2=3, 2+3=5, 3+5=8, 5+8=13, 8+13=21, … That is Fibonacci’s Series.

Australia discovered to its sorrow how rapidly the Series’ numbers can rise. After the first few generations the rabbit population grows literally exponentially (Those two words are misused way too often but they each apply here.).

Exponential growth appears when a process operates periodically on something to produce more of the same thing. The periodicity can be timewise, like seasonal years or generations of living things, or spacewise, like successive outward divisions of the cells that give rise to sunflower seeds or snail shells. If the something comes in units, like rabbit pairs, the growth comes in integers. If the units are small and the numbers are large, like yeast cells in a beer vat, it’s easier to express the growth as a percentage. The small‑unit numbers eventually increase as en/R, where R=½(1+√5). Compound interest? Same mechanism, same mathematics, just more arithmetic.

Back to the 12th century. Papa Bonacci was a merchant engaged in commerce between Pisa and Algiers. Young Leonardo grew up in his Dad’s North African trading post, first observing and later negotiating with Arabian traders who used a number system they’d gotten from Hindu merchants. He was smart enough to appreciate the power inherent in the Hindu‑Arabic number system (powers‑of‑10 positional notation, with a zero indicator to mark each slot where a number lacks a contribution from that 10‑power). In later years he wrote it up, in Liber Abaci.

At the dawn of the 13th century, Europe had been using Roman numerals for a millennium. The Italian trading empires of the 15th century could not have been built without the rigor, discipline and reliability of double‑entry bookkeeping. Can you imagine doing double‑entry accounting, much less compound interest calculations, with Roman numerals? I can’t, either. Europe’s commercial interests simply couldn’t have developed without the trustworthy record‑keeping techniques based on Liber Abaci‘s arithmetic principles. It’s easy to find realistic through‑lines from Fibonacci’s book to most of modern technology.

Today we say that computing is all ones and zeros. Fibonacci brought us the zeroes.

Rabbit image by JJ Harrison,
under CC ASA 3.0 license
  • 547 is a prime number. This the 547th post in this blog, a suitable spot for me to hit “Pause” so I can free up time for another project. That one promises plenty of rabbit holes like the ones I’ve explored while having fun researching topics here. There are limits. In the future I’ll be posting here irregularly rather than on the weekly schedule I’ve kept to for a decade. Stay in touch.

~ Rich Olcott

Cozy Numbers

On By rolcottIn General: Fun Stuff, Mathematics: Dimensions, UncategorizedLeave a comment

If you’ve followed this blog for more than a year (in which case, thanks), you’ve probably noticed that I like numbers. As a kid I got a thrill when I figured out why (111 111 111)² is the amazingly symmetrical 12 345 678 987 654 321. Like many other numberphiles I’m fascinated by special categories like primes (no divisor other than unity and the number itself) and figurate numbers (counting the dots that make a geometrical pattern like concentric hexagons).

Every number has charms of its own (2025 is a delicious example), but 2026 doesn’t seem like it’s particularly special. 2026 is 2×1013, so it’s not prime nor is it the square or power of some smaller number. It’s not palindromic like 1991 and 2002 are. In binary it’s 111 1110 10102 — not very interesting. It can be written as 201013 , which is just silly. But 2026 does turn out to be special, in a special way — it’s a Beprisque number and they’re rare.

The On-line Encyclopedia of Integer Sequences®, a.k.a. OEIS, does for whole numbers what Bartlett’s Familiar Quotations does for words: it’s a venerable compendium of usage in context, with citations. An OEIS search for “2026” found 270 sequences that include the number. Most are technical or abstruse to a fault. Entry A118454, for example, identifies 2026 as the algebraic degree of the onset of the logistic map’s 11th bifurcation. Don’t ask.

Among my search hits was A216840, “palindromic numbers of 3 digits in two bases.” It’s cool that 202610 is bcb13 and also a4a14. Unfortunately, my math software’s number‑base converter has only 36 available digits (0‑9, a‑z) so it can’t display numbers in base‑37 or worse.

My favorite entry in the set is A163492: Beprisque numbers are integers such that their two immediate neighbors on the number line are a perfect square and a prime. 10 is Beprisque because it’s nestled between 9=3² and 11 (a prime). So is 2026, sitting between 2025=45² and 2027 (prime).

“Beprisque” — looks kind of French, doesn’t it? Maybe named after one of those 18th century scientist‑aristocrats that Robespierre killed off? Nope, it’s simply a mash‑up of “between prime and square.”

This being a New Year post, I couldn’t resist mentioning the New Year monkey. Every year the financial press services trot the poor thing out, give it a handful of darts with instructions to fling them it at the Wall Street Journal‘s stock listing or some such. The monkey’s acumen is assessed by how much its dart‑selected equities have grown (or not) over the past year. Usually the monkey’s score rates near or even better than that of the “professional” stock pickers, which is supposed to tell us something.

Suppose we were to direct the monkey to toss its darts at the number line. How well would it do at hitting Beprisque numbers? How dense are the primes and squares and what are the odds that one from one category is exactly two seats away from one from the other?

It depends on how much of the line the monkey can aim at. The range between 1 and 100 has 10 squares (10% coverage), 25 primes (25% coverage) and 9 Beprisques (1, 2, 3, 8, 10, 24, 48, 80, 82). Nine out of a hundred is 9% coverage; looks good. But widen the range to 1000 and the coverages drop — 31 squares (3%), 168 primes (17%) and 17 Beprisques — 10 times the range but fewer than twice the hits. Extend the number line to 1 000 000 and the percentages get even worse: 0.1% squares, 7.9% primes and only 0.022 6% Beprisques. The Beprisque coverage drops to 0.007 2% if the monkey’s target range shifts to the span between one and two million.

Why so few? On the average primes are further apart for bigger numbers because the prime count grows about 15% more slowly than the range does. Meanwhile, the separation between successive squares grows linearly as the squared number increases:
  (n+1)² – n² = n²+2n+1 – n² = 2n+1
The two trends conspire to thin out those cozy sequences. Give the poor monkey an infinite range and its odds on a square‑Beprisque‑prime triplet evaporate like a certain team’s championship hopes.

~ Rich Olcott

Does Tomorrow Exist?

On By rolcottIn Cosmology, General: Fun Stuff, UncategorizedLeave a comment

Power’s back on. The elevator lets us out on the second floor where we proceed into Eddie’s Pizza Place. We order, find a table, and Cathleen cocks an eyebrow. “So, Anne, you’re a time‑traveler?”

“Lots of dimensions, actually. Time, space, probability… Once I accidentally jumped into a Universe where the speed of light was a lot slower. I was floating near a planet in a small system whose sun flared up but it took a long, long time for the flash to reflect off the planet behind me. Funny, I felt stiffer than usual. It was a lot harder to move my arms. I avoid cruising dimensions like that one.”

<The other eyebrow goes up> “Wait, what’s the speed of light got to do with dimensions? And why would it affect moving your arms?”

My cue. “Physics has a long‑standing problem with the speed of light and a dozen or so other fundamental numbers like Newton’s gravitational constant and Einstein’s cosmological constant. We can measure them but we can’t explain why they have the values they do. Okay, the speed of light depends on electric and magnetic force constants, but we can’t explain those, either — the rabbit hole just gets deeper. In practice, our Laws of Physics are a set of equations with blanks for plugging in the measured values. People have suggested that there’s a plethora of alternate universes with the same laws of physics we have but whose fundamental constants can vary from ours. Apparently Anne traveled along a dimension that connects universes with differing values of lightspeed.”

“I suppose. … But the arm‑moving part?”

“An effect of Special Relativity. Newton’s Second Law a=F/m says that an object’s acceleration equals the applied force per unit mass. That works fine in every‑day life but not when the object’s velocity gets close to lightspeed.” <jotting on a paper napkin> “I don’t see Vinnie nearby so here’s the relativistic equation: a=(F/m)×√[1–(v/c)²]. The v/c ratio compares object velocity to lightspeed. The Lorentz factor, that square root, is less than 1.0 for velocities less than lightspeed. This formula says a given amount of force per unit mass produces less acceleration than Newton would expect. How much less depends on how fast you’re already going. In fact, the acceleration boost approaches zero when v approaches c. With me?”

“If your factor’s exactly zero, then even an infinite force couldn’t accelerate you, right? But what’s all that got to do with my arm?”

“Zero acceleration, mm‑hm. Suppose your arm’s rest mass and muscle force per unit mass are the same in the slow‑light universe as they are in ours. The Lorentz factor’s different. Lightspeed in our Universe is 3×108 m/s. Suppose you wave your arm at 10 m/s. Your Lorentz factor here is √[1–(10/3×108)²] which is so close to unity we couldn’t measure the difference. Now suppose ‘over there’ the lightspeed is 20 m/s and you try the same wave. The Lorentz formula works out to √[1–(10/20)²] or about 85%. That wave would cost you about 15% more effort.”

<Both eyebrows down> “Have you tried going forward in time?”

“Sure, but I can’t get very far. It’s like I’ve got an anchor ‘here.’ I can move back ‘here’ from the past, no problem, but when I try to move forward from ‘here’ even a day or so … It’s hard to describe but as I go everything feels fuzzier and then I get queasy and have to stop. Do you have an explanation for that, Sy?”

“Well, an explanation but I can’t tell you it’s correct. Einstein thought it conflicts with Relativity, other people disagree. According to the growing block theory of time, the past and present are set and unchanging but the future doesn’t exist until we get there. Your description sounds like a build on that theory, like maybe the big structures extend a bit beyond us but their quantum details are still chaotic until time catches up with them. There are a few reports of lab experiments that would be consistent with something like that but it’s early days in the research.”

“As the saying goes, ‘Time will tell,’ right, Sy?”

“Mm-hm, lo que será, será.“

~ Rich Olcott

A Shot Through The Dark

On By rolcottIn Cosmology, General: Fun Stuff, UncategorizedLeave a comment

<THUNK!!> “Oh, dear. Is this the same elevator that you and Vinnie got trapped in, Sy?”

“Afraid so, Cathleen, but at least we had lights. This looks like a power outage, not a stuck door mechanism. Calling the building super probably won’t help. Hope you’re okay being stuck in the dark.”

“I’m an astronomer, Sy. A dark night’s my best thing. Remember the time we got locked with no light in my Mom’s closet?”

<chuckle> “Mm-hm. It was our pretend spaceship to Mars. We had no idea that closet had a catch we couldn’t reach. We were stuck there until your Mom came home. <sigh> We’ll have to wait ’til power comes back.”

<FZzzzzttPOP!!> … <then a voice like molten silver> “Oh, there you are, Sy! I’ve been looking all over for you. Who’s this?”

“Been a while, Anne. This is Cathleen. Cathleen, meet Anne. Anne’s an … explorer.”

“Ooo, where do you explore? For that matter, how did you get in here, and why is your dress (is it satin?) glowing like that?”

“Yes, it is satin, at the moment. It figures out whatever I need and makes that happen. It’s glowing because we’re in the dark.”

“I suspect your dress saved you when you met anti‑Anne.”

“Auntie Anne?”

“No, Cathleen, anti‑Anne, another me in the anti‑Universe. You might be right, Sy. It would have held anti‑Earth’s anti‑atoms away long enough for me to escape annihilation. Maybe I should explain.”

“I wish you would.”

“Wellll, I’ve got this super‑power for jumping across spacetime. Sy helped me calibrate my jumps and we even worked out how I can change size and use entropy to navigate between probabilities. So I explore everywhere and everywhen and that’s how I got into this elevator.” <brief fizzing sound> “Don’t worry, power will be back on soon but we’ve got time for Sy to explain my most recent experience.”

“Ah‑boy, now what?”

“Well, it seemed like a fun thing to do — go back to the earliest time I could, maybe even watch the Big Bang. I did some reading so I had an idea of what to expect as I dove down the time axis — gas clouds collapsing with glittering bursts of star formation, stars collecting into galaxies, galaxies streaming by like granular gas — so beautiful, especially because I can tweak my time rate and watch it all in motion!”

“And did you see all that?”

“Oh, yes, but then I hit a wall I couldn’t get past and I don’t understand why.”

“What were things like just before you hit the wall?”

“This was just beyond when I saw the very first stars turning on. There were vague clouds glowing here and there but basically the Universe became pitch black, no light at all for a while until the background started to glow with a very deep red just before I was blocked.”

“Ah. Cathleen, this is more your bailiwick than mine. Anne, Cathleen teaches Astronomy and Cosmology.”

“Just as a check, Anne, do you know exactly how far into the past you got?”

“Sorry, no. My time sense is pretty well calibrated for hours‑to‑centuries but this was billions of years. You probably know when I was better than I do.”

“On the evidence, I’d say you got 99.98% of the way back to your goal, nearly to the beginning of the Dark Age.”

“Dark Age? I’ve been there — 10th‑century Earth, bad times for everyone unless you were at the top of the heap but you wouldn’t stay there long. But I was too far out in space to see Earth. I couldn’t even pick out the Milky Way.”

“No, this was the Universe’s Dark Age, a couple hundred million years between when atoms formed and stars formed. Nothing could make new light. The Dark Age started at Big Bang plus 370 000 years when temperature cooled to 4000 K. The dark red you saw everywhere was atoms emitting blackbody radiation at 4000 K. Just 0.01% further into the past, the Universe was a billion‑degree quark plasma where not even atoms could survive. No wonder your dress wouldn’t let you enter.”

<THUNK!!> “Oh, good, power’s back on. We have light again!”

~ Rich Olcott

A No-Charge Transaction

On By rolcottIn Cosmology, Crazy Theories, Physics: Light and Relativity, UncategorizedLeave a comment

“I ain’t done yet, Sy. I got another reason for Dark Matter being made of faster‑then‑light tachyons.”

“I’m still listening, Vinnie.”

“Dark Matter gotta be electrically neutral, right, otherwise it’d do stuff with light and that doesn’t happen. I say tachyons gotta be neutral.”

“Why so?”

“Stands to reason. Suppose tachyons started off as charged particles. The electric force pushes and pulls on charges hugely stronger than gravity pulls—”

“1036 times stronger at any given distance.”

“Yeah, so right off the bat charged tachyons either pair up real quick or they fly away from the slower‑than‑light bradyon neighborhood leaving only neutral tachyons behind for us bradyon slowpokes to look at.”

“But we’ve got un‑neutral bradyon matter all around us — electrons trapped in Earth’s Van Allen Belt and Jupiter’s radiation belts, for example, and positive and negative plasma ions in the solar wind. Couldn’t your neutral tachyons get ionized?”

“Probably not much. Remember, tachyon particles whiz past each other too fast to collect into a star and do fusion stuff so there’s nobody to generate tachyonic super‑high‑energy radiation that makes tachyon ions. No ionized winds either. If a neutral tachyon collides with even a high-energy bradyon, the tachyon carries so much kinetic energy that the bradyon takes the damage rather than ionize the tachyon. Dark Matter and neutral tachyons both don’t do electromagnetic stuff so Dark Matter’s made of tachyons.”

“Ingenious, but you missed something way back in your initial assumptions.”

“Which assumption? Show me.”

“You assumed that tachyon mass works the same way that bradyon mass does. The math says it doesn’t.” <grabbing scratch paper for scribbling> “Whoa, don’t panic, just two simple equations. The first relates an object’s total energy E to its rest mass m and its momentum p and lightspeed c.”

E² = (mc²)² + (pc)²

“I recognize the mc² part, that’s from Einstein’s Equation, but what’s the second piece and why square everything again?”

“The keyword is rest mass.”

“Geez, it’s frames again?”

“Mm‑hm. The (mc²)² term is about mass‑energy strictly within the object’s own inertial frame where its momentum is zero. Einstein’s famous E=mc² covers that special case. The (pc)² term is about the object’s kinetic energy relative to some other‑frame observer with relative momentum p. When kinetic energy is comparable to rest‑mass energy you’re in relativity territory and can’t just add the two together. The sum‑of‑squares form makes the arithmetic work when two observers compare notes. Can I go on?”

“I’m still waitin’ to hear about tachyons.”

“Almost there. If we start with that equation, expand momentum as mass times velocity and re‑arrange a little, you get this formula

E = mc² / √(1 – v²/c²)

The numerator is rest‑mass energy. The v²/c² measures relative kinetic energy. The Lorentz factor down in the denominator accounts for that. See, when velocity is zero the factor is 1.0 and you’ve got Einstein’s special case.”

“Give me a minute. … Okay. But when the velocity gets up to lightspeed the E number gets weird.”

“Which is why c is the upper threshold for bradyons. As the velocity relative to an observer approaches c, the Lorentz factor approaches zero, the fraction goes to infinity and so does the object’s energy that the observer measures.”

“Okay, here’s where the tachyons come in ’cause their v is bigger than c. … Wait, now the equation’s got the square root of a negative number. You can’t do that! What does that even mean?”

“It’s legal, when you’re careful, but interpretation gets tricky. A tachyon’s Lorentz factor contains √(–1) which makes it an imaginary number. However, we know that the calculated energy has to be a real number. That can only be true if the tachyon’s mass is also an imaginary number, because i/i=1.”

“What makes imaginary energy worse than imaginary mass?”

“Because energy’s always conserved. Real energy stays that way. Imaginary mass makes no sense in Newton’s physics but in quantum theory imaginary mass is simply unstable like a pencil balanced on its point. The least little jiggle and the tachyon shatters into real particles with real kinetic energy to burn. Tachyons disintegrating may have powered the Universe’s cosmic inflation right after the Big Bang — but they’re all gone now.”

“Another lovely theory shot down.”

~ Rich Olcott

Got To Be Good-lookin’ ‘Cause He’s So Hard To See

On By rolcottIn Cosmology, Crazy Theories, UncategorizedLeave a comment

I’ll be sorry when Acme Building’s management swaps out our old‑style door locks for electronic ones. Vinnie has such fun lock‑picking his way past my office door in the morning. “Morning, Vinnie.”

“Morning, Sy. Hey, I got a new Crazy Theory for you. Nobody knows what Dark Matter is, right?”

“Right. All we know is that it has about five times as much mass as normal matter so it participates in gravitational interactions. Some of it seems to gather in spherical halos around galaxies and some of it seems to collect in spikes near their centers. Cosmologists are arguing about whether or not Dark Matter is particles, much less how they’d be quantized. And we call it Dark because it absolutely doesn’t care about electromagnetism.”

“That’s what I thought. I remember you said if Dark Matter did play with light waves at all it’d block our view of the CMB. So yeah, absolute. Good.”

“I gather your theory is about Dark Matter.”

“Mm-hm. I thought of a way that all that mass could be hiding in plain sight except we can’t see it.”

“Alright, I’m listening.”

“Tachyons.”

“Come again?”

“Tachyons — particles that fly around faster than light. I read an article about ’em. Some people say they can’t exist but hear me out, okay? The reason they’re not supposed to exist is ’cause it would take an infinite amount of energy to boost something up past lightspeed. I got that, but suppose they were born above lightspeed, back when the Big Bang singularity had energy packed so tight the Physics laws we know don’t apply. A lot of particles got flung out below lightspeed, but maybe even more got flung out above it.”

“What does this have to do with dark matter?”

“I’m gettin’ there. The thing with tachyons is, the article said it’d take infinite energy to slow one down to lightspeed. A tachyon rock hits a slow rock, it don’t stop ’cause the slow rock don’t have the juice for that. The collision may take a little energy from the tachyon rock but that just changes its trajectory.”

“Mmm, those tachyon rocks can’t be a thing. The — what can I call it? slow matter?”

“The article called ’em bradyons.”

“Thanks. We know that 92% of all … bradyonic atoms in the Universe are hydrogens. Rocks are made of silicon, oxygen and other atoms that are even heavier. Everything heavier than hydrogen and maybe some helium was created by nuclear reactions inside a star. Tachyonic atoms zooming beyond lightspeed couldn’t gather together to form a star or even join one. No significant tachyonic fusion, no tachyonic rocks.”

“Okay, they all stay tachy‑hydrogen, still not a problem. The point is, there could be a lot of them and they could add up to a lot of mass. So the next thing I asked is, where would tachyons hang out? Gotta be around galaxies, but being tachyons going super‑lightspeed they can’t just hang, they orbit around the centers. They’d spend the most time where they go slowest which is where they’re farthest away ’cause that’s how orbits work. But they’d be thickest close in ’cause of gravity but that’s where they go fastest.”

“Cute, so you’re predicting galaxies with halos of tachyons, plus spikes of them at each center. That just happens to be the dark matter distribution the astronomers find.”

“It gets better, Sy. I’m not so sure of this because math, but it feels right. I don’t think tachyons can do electromagnetism things.”

“Why not?”

“No blue glow — you know, that blue glow in nuclear reactors when electrons go through the cooling water faster than light?”

“Cherenkov radiation, happens when fast electrons polarize the water. The polarizing slows light in water relative to a vacuum.”

“Right, but tachyons in space travel through vacuum. They ought to polarize the vacuum like what fast electrons do to water. Electromagnetic tachyons orbiting galaxies ought to make a blue glow but there isn’t one, so tachyons don’t do electromagnetism things and that makes them Dark Matter.”

“You’re going to have to do better than that, Vinnie. Absence of evidence just might be evidence of absence. Maybe they’re not there to begin with.”

~ Rich Olcott

The Time Is Out of Joint

On By rolcottIn Cosmology, Crazy Theories, UncategorizedLeave a comment

Vinnie galumphs over to our table. “Hi, guys. Hey, Sy, I just read your Confluence post. I thought that we gave up on things happening simultaneous because of Einstein and relativity but I guess that wasn’t the reason.”

“Oh, things do happen simultaneously, no‑one claims they don’t, it’s just that it’s impossible for two widely‑separated observers to have evidence that two widely‑separated events happened simultaneously. That’s a very different proposition.”

“Ah, that makes me feel better. The ‘nothing is simultaneous‘ idea was making me itchy ’cause I know for sure that a good juggler lets go with one hand just as they’re catching with the other. How’s Einstein involved then?”

“Lightspeed’s a known constant. Knowing distance and lightspeed lets you calculate between‑event time, right? The key to simultaneity was understanding why lightspeed is a constant. We’d known lightspeed wasn’t infinite within the Solar System since Rømer’s time, but people doubted his number applied everywhere. Maxwell’s theory of electromagnetism derived lightspeed from the properties of space itself so it’s universal. Only in Newton’s Universe was it possible for two distant observers to agree that two also‑distant events were simultaneous.”

“Why was Newton’s Universe special?

“Space held still and didn’t bend. Astronomers A and B had a stable baseline between them. After measuring the baseline with light they could measure the angles each observed between the events. Some trigonometry let them send each other congratulatory messages on seeing a simultaneous pair of incidents. After Einstein’s work, they knew better.”

“It’s frames again, ain’t it?”

“Of course, Vinnie. A‘s frame is almost certainly moving relative to B‘s frame. Motion puts the Lorentz relativity factor into the game, making each astronomer’s clock run faster than the other’s. Worse, each astronomer sees that the other’s yardsticks are too short.”

Jeremy gives me a confused look.

“Space compression goes along with time dilation, Jeremy. Professor Hanneken will explain it all when your class gets to that unit. Bottom line, things can happen simultaneously in Einstein’s Universe, but no‑one can agree on which things.”

“Wait, if every frame has its own time‑rate, how can two spaceships rendezvous for an operation?”

“Good question, Jeremy. Einstein had an answer but complications hide under the covers. He suggested that A start a timer when sending a light pulse to a mirror at B. A waits for the reflection. B starts a timer when they see A‘s pulse. A measures the pulse’s round‑trip time. Each creates a clock that advances one tick for half of the round-trip time. B sets their clock back by one tick. That done, they agree to meet some number of ticks later.”

“Hmm… That should work, but you said there are complications.”

“There are always complications. For instance, suppose B is slingshotting around a black hole so that pulse and reflection travel different pathlengths. Or suppose one frame is rotating edge‑on to the other. In practice the ships would re‑sync repeatedly while approaching the rendezvous point.”

Vinnie erupts. “HAW! Successive approximation again!”

“Indeed. If we could extend the method to more than two participants we’d have a true Universal Coordinated Time.”

“Don’t we have that, Mr Moire? The Big Bang happened 14 billion years ago. Couldn’t we measure time from that?”

“Sort of. Last I looked the number was 13.787 plus‑or‑minus 20 million years. Too much slop for an instantaneous fleet‑level rendezvous like the final battle scene in StarTrek:Picard. But you’ve brought up an interesting question for a Crazy Theories seminar. One of Cosmology’s deepest unsolved questions is, ‘How does inertia work?’ Do you remember Newton’s First Law?”

<closes eyes> “In an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.“

“Right. In other words, every object resists change to its current steady motion along a geodesic. Why is that? There’s no coherent, well‑founded, well‑tested theory. Einstein liked Mach’s Principle, which says inertia exists because every object is attracted through space to all the mass in the Universe. Suppose there’s a Mach’s Principle for Time, saying that objects squirt up the Time axis because they’re repelled by all the mass in the Universe.”

Vinnie hoots, “Bo-o-o-ohh-GUS!”

~ Rich Olcott

Hillerman, Pratchett And Narrativium

On By rolcottIn Astronomy, General: Fun Stuff, UncategorizedLeave a comment

No-one else in the place so Jeremy’s been eavesdropping on my conversation with Cal. “Lieutenant Leaphorn says there are no coincidences.”

“Oh, you’ve read Tony Hillerman’s mystery stories then?”

“Of course, Mr Moire. It’s fun getting a sympathetic outsider’s view of what my family and Elders have taught me. He writes Leaphorn as a very wise man.”

“With some interesting quirks for a professional crime solver. He doesn’t trust clues, yet he does trust apparent coincidences enough to follow up on them.”

“It does the job for him, though.”

“Mm‑hm, but that’s in stories. Have you read any of Terry Pratchett’s Discworld books?”

“What are they about?”

From Terry Pratchett’s book
Carpe Jugulum

“Pretty much everything, but through a lens of laughter and anger. Rather like Jonathan Swift. Pratchett was one of England’s most popular authors, wrote more than 40 novels in his too‑brief life. He identified narrativium as the most powerful force in the human universe. Just as the nuclear strong force holds the atomic nucleus together using gluons and mesons, narrativium holds stories together using coincidences and tropes.”

“Doesn’t sound powerful.”

“Good stories, ones that we’d say have legs, absolutely must have internal logic that gets us from one element to the next. Without that narrative flow they just fall apart; no‑one cares enough to remember them. As a writer myself, I’ve often wrestled with a story structure that refused to click together — sparse narrativium — or went in the wrong direction — wayward narrativium.”

“You said ‘the human universe’ like that’s different from the Universe around us.”

“The story universe is a multiverse made of words, pictures and numbers, crafted by humans to explain why one event follows another. The events could be in the objective world made of atoms or within the story world itself. Legal systems, history, science, they’re all pure narrativium. So is money, mostly. We don’t know of anything else in the Universe that builds stories like we do.”

“How about apes?”

“An open question, especially for orangutans. One of Pratchett’s important characters is The Librarian, a university staff member who had accidentally been changed from human to orangutan. He refuses to be restored because he prefers his new form. Which gives you a taste of Pratchett’s humor and his high regard for orangutans. But let’s get back to Leaphorn and coincidences.”

“Regaining control over your narrativium, huh?”

“Guilty as charged. Leaphorn’s standpoint is that there are no coincidences because the world runs on patterns, that events necessarily connect one to the next. When he finds the pattern, he solves the mystery.”

“Very Diné. Our Way is to look for and restore harmony and balance.”

“Mm‑hm. But remember, Leaphorn is only a character in Hillerman’s narrativium‑driven stories. The atom‑world may not fit that model. A coincidence for you may not be a coincidence for someone else, depending. Those two concurrent June novas, for example. For most of the Universe they’re not concurrent.”

“I hope this doesn’t involve relativistic clocks. Professor Hanneken hasn’t gotten us to Einstein’s theories yet.”

Adapted from images by
IAU and Sky & Telescope magazine
(Roger Sinnott & Rick Fienberg)
CC BY 3.0

“No relativity; this is straight geometry. Rømer could have handled it 350 years ago.” <brief tapping on Old Reliable’s screen> “Here’s a quick sketch and the numbers are random. The two novas are connected by the blue arc as we’d see them in the sky if we were in Earth’s southern hemisphere. We live in the yellow solar system, 400 lightyears from each of them so we see both events simultaneously, 400 years after they happened. We call that a coincidence and Cal’s skywatcher buddies go nuts. Suppose there are astronomers on the white and black systems.”

<grins> “Those four colors aren’t random, Mr Moire.”

<grins back> “Caught me, Jeremy. Anyway, the white system’s astronomers see Vela’s nova 200 years after they see the one in Lupus. The astronomers in the black system record just the reverse sequence. Neither community even thinks of the two as a pair. No coincidence for them, no role for narrativium.”

~ Rich Olcott

  • This is the 531st post in an unbroken decade‑long weekly series that I originally thought might keep going for 6 months. <whew!>

Confluence

On By rolcottIn Astronomy, Astronomy: Multi-messenger, General: Fun Stuff, UncategorizedLeave a comment

“My usual cup of — Whoa! Jeremy, surprised to see you behind the counter here. Where’s Cal?”

“Hi, Mr Moire. Cal just got three new astronomy magazines in the same delivery so he’s over there bingeing. He said if I can handle the pizza place gelato stand he can trust me with his coffee and scones. I’m just happy to get another job ’cause things are extra tough back on the rez these days. Here’s your coffee, which flavor scone can I get for you?”

“Thanks, Jeremy. Smooth upsell. I’ll take a strawberry one. … Morning, Cal. Having fun?”

“Morning, Sy. Yeah, lotsa pretty pictures to look at. Funny coincidence, all three magazines have lists of coincidences. This one says February 23, 1987 we got a neutrino spike from supernova SN 1987A right after we saw its light. The coincidence told us that neutrinos fly almost fast as light so the neutrino’s mass gotta be pretty small. 1987’s also the year the Star Tours Disney park attractions opened for the Star Wars fans. The very same year Gene Roddenberry and the Paramount studio released the first episodes of Star Trek: The Next Generation. How about that?”

“Pretty good year.”

“Mm‑hm. Didja know here in 2025 we’ve got that Mercury‑Venus‑Jupiter-Saturn‑Uranus‑Neptune straight‑line arrangement up in the sky and sometimes the Moon lines up with it?”

“I’ve read about it.”

“Not only that, but right at the September equinox, Neptune’s gonna be in opposition. That means our rotation axis will be broadside to the Sun just as Neptune will be exactly behind us. It’ll be as close to us as it can get and it’s face‑on to the Sun so it’s gonna be at its brightest. Cool, huh?”

“Good time for Hubble Space Telescope to take another look at it.”

“Those oughta be awesome images. Here’s another coincidence — Virgo’s the September sign, mostly, and its brightest star is Spica. All the zodiac constellations are in the ecliptic plane where all the planet orbits are. Planets can get in the way between us and Spica. The last planet to do that was Venus in 1783. The next planet to do that will be Venus again, in 2197.”

“That’ll be a long wait. You’ve read off things we see from Earth. How about interesting coincidences out in the Universe?”

“Covered in this other magazine’s list. Hah, they mention 1987, too, no surprise. Ummm, in 2017 the Fermi satellite’s GRB instrument registered a gamma‑ray burst at the same time that LIGO caught a gravitational wave from the same direction. With both light and gravity in the picture they say it was two neutron stars colliding.”

“Another exercise in multi-messenger astronomy. Very cool.”

“Ummm … Galaxy NGC 3690 shot off two supernovas just a few months apart last year. Wait, that name’s familiar … Got it, it’s half of Arp 299. 299’s a pair of colliding galaxies so there’s a lot of gas and dust and stuff floating around to set off stars that are in the brink. If I remember right, we’ve seen about eight supers there since 2018.”

“Hmm, many events with a common cause. Makes sense.”

“Oh, it’s a nice idea, alright, but explain V462 Lupi and V572 Velorum. Just a couple months ago, two novas less than 2 weeks apart in two different constellations 20 degrees apart in the sky. Bright enough you could see ’em both with good eyes if you were below the Equator and knew where to look and looked in the first week of June. My skywatcher internet buddies down there went nuts.”

“How far are those events from us?”

“The magazine doesn’t say. Probably the astronomers are still working on it. Could be ten thousand lightyears, but I’d bet they’re a lot closer than that.”

“On average, visible stars are about 900 lightyears away. Twenty degrees would put them about 300 lightyears apart. They’re separated by a slew of stars that haven’t blown up. One or both could be farther away than that, naturally. Whatever, it’s hard to figure a coordinating cause for such a distant co‑occurrence. Sometimes a coincidence is just a coincidence.”

Adapted from images by
IAU and Sky & Telescope magazine
(Roger Sinnott & Rick Fienberg)
CC BY 3.0

~ Rich Olcott

Black, White And Wormy

On By rolcottIn Cosmology, Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

“Whaddaya mean, Sy, if white holes exist? You just told me how they’re in the equations just like black holes.”

“Math gives us only models of reality, Vinnie. Remarkably good models, some of them, but they’re only abstractions. Necessarily they leave out things that might skew math results away from physical results or the other way around. Einstein believed his math properly reflected how the Universe works, but even so, he doubted that black holes could exist. He didn’t think it’d be possible to collect that much mass into such a small space. Two decades after he said that, Oppenheimer figured out how that could happen.”

“Oppenheimer like the A‑bomb movie guy?”

“Same Oppenheimer. He was a major physicist even before they put him in charge of the Manhattan Project. He did a paper in 1939 showing how a star‑collapse could create the most common type of black hole we know of. Twenty‑five years after that the astronomers found proof that black holes exist.”

“Well, if Einstein was wrong about black holes, why wasn’t he wrong about white holes?”

“We need another Oppenheimer to solve that. So far, no‑one has come up with a mechanism that would create a stand‑alone white hole. That level of stress on spacetime requires an enormous amount of mass‑energy in a tiny volume. Whatever does that must somehow do it with a time‑twist opposite to how a black hole is formed. Worse yet, by definition the white hole’s Event Horizon leaks matter and energy. The thing ought to evaporate almost as soon as it’s formed.”

“I heard weaseling. You said, ‘a stand‑alone white hole,’ like there’s maybe another kind. How about that?”

“Could be, maybe not, depending on who’s talking and whether or not they’re accounting for magnetic fields, neutrinos or quantum effects. The discussion generally involves wormholes.”

“Wormholes.”

“Mm-hm. Some cosmologists think that wormholes might bridge between highly stressed points in spacetime. Black hole or white, the stress is what matters. The idea’s been around nearly as long as our modern idea of black holes. No surprise, ‘wormhole’ was coined by John Archibald Wheeler, the same guy who came up with the phrases ‘black hole’ and ‘quantum foam’.”

“Quantum—. Nope, not gonna bite. Get back to white holes.”

“I’m getting there. Anyway, the relativity theory community embraced black holes, white holes and wormholes as primary tools for studying how spacetime works.”

“How’re they gonna do that? That squib Cal showed me said we’ve never seen a white hole.”

“Fair question. Last I heard, the string theory community confidently predicted 10500 different Universes with little hope of narrowing the field. In contrast, relativity theory is firmly constrained by well‑founded math, a century of confirmation from experimental tests and a growing amount of good black hole data. Perfectly good math says that wormholes and white holes could form but only under certain unlikely conditions. Those conditions constrain white holes like Oppenheimer’s conditions constrained forming a stellar‑size black hole.”

“So how do we make one?”

“We don’t. If the Universe can make the right conditions happen somewhere in spacetime, it could contain white holes and maybe a network of wormholes; otherwise, not. Maybe we don’t see them because they’ve all evaporated.”

“I remember reading one time that with quantum, anything not forbidden must happen.”

“Pretty much true, but we’re not talking quantum here. Macro‑scale, some things don’t happen even though they’re not forbidden.”

“Name one.”

“Anti‑matter. The laws of physics work equally well for atoms with positive or negative nuclear charge. We’ve yet to come up with an explanation for why all the nuclear matter we see in the Universe has the positive‑nucleus structure. The mystery’s got me considering a guess for Cathleen’s next Crazy Theories seminar.”

“Oh, yeah? Let’s have it.”

“Strictly confidential, okay?”

“Sure, sure.”

“Suppose the Big Bang’s chaos set up just the right conditions to make a pair of CPT‑twin black holes, expanding in opposite directions along spacetime’s time dimension. Suppose we’re inside one twin. Our time flows normally. If we could see into the other twin, we’d see inside‑out atoms and clocks running backwards. From our perspective the twin would be a white hole.”

“Stay outta that wormhole bridge.”

~ Rich Olcott