Category: Mathematics: Dimensions

Dimensional venturing, Part 3 – Klein’s thingy

On By rolcottIn Cosmology, Mathematics: Dimensions, Uncategorized2 Comments

The Klein bottle is one of the most misunderstood objects in popular math.  Let’s start with the name.  When he initially described the object Herr Doktor Professor Felix Klein said it was a surface.  Being German and writing in German, he used the word Fläche (note the two little dots over the a).  When his paper was translated to English, the translator noticed the shape of the thing but didn’t notice those two little dots.  He misread the word as Flasche, meaning flask or bottle, and the latter word stuck.

Cut Torus
Adapted from “Torus”. Licensed under Public Domain via Commons – https://commons.wikimedia.org/wiki/File:Torus.png

So who was Herr Klein and what was it that he wrote about?  One of the world’s foremost mathematicians in the last quarter of the 19 Century, he specialized in geometry, complex analysis and mathematical physics.  Among his other accomplishments was that as director of a research center at Georg-August-Universität Göttingen in 1895 he supervised Germany’s first Ph.D. thesis written by a woman (Grace Chisholm Young).

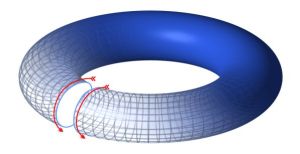
As a small part of one of his many papers he noted that a cylinder could be deformed in two different ways to connect its two ends. The first way is to simply bend it around in a circle to form a torus (or bicycle tire or doughnut, depending on how hungry you are.)

IssueThe other way is more of a challenge — bringing one end to meet the other from inside the cylinder.  The problem is that in the context of Klein’s work, he wasn’t “allowed” to pierce the cylinder’s surface to get it there.  Klein’s solution was simple  — swing it in through the fourth dimension.  Sounds like a cheat, doesn’t it?

Actually, the cheat is in the way KKleinthat the Klein bottle is usually represented.  When the glass artisan created this example, he probably brought one tube up from the bottom, sealed it to the side wall, blew a hole in the side wall at that location, and then brought the outside tube around to join there.  That hole would not have satisfied Herr Klein.

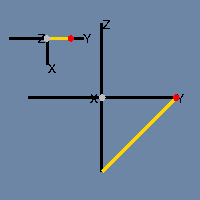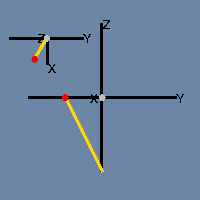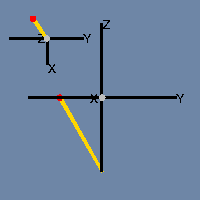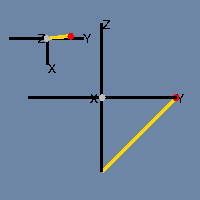
If you’ve looked at my previous post in this series you probably have a pretty good idea of how he would have preferred his Fläche to be depicted — as an animation which exploits time as the fourth dimension.  So here you have it.

Suppose the figure’s wall sprouts from a bud somewhere near the intersection point.  After the figure has grown for a while, the earliest section of the wall begins to recede, disappearing like the Cheshire Cat but leaving its ever-expanding smile behind.  By the time the growth front gets to where the bud was, there’s nothing there to intersect.

Reverse Klein If you opt to build the “bottle” in 4-space, there’s no problem getting those two ends of the cylinder to join up.  A shape that’s impossible to build in three dimensions is easy-peasy (with a little planning) in four.

Yeah, yeah, the Klein bottle has lots of interesting properties, like not having an inside, but we’ll defer talking about them for a while.

Next week, getting past that pesky four-dimension limitation.

~~ Rich Olcott

Dimensional venturing, Part 2 – Twirling in 4-space

On By rolcottIn General: Fun Stuff, Mathematics: Dimensions, Uncategorized4 Comments

Last week we introduced the tesseract, which is to a cube what a cube is to a square — an extension into one more dimension.  That’s why it’s also called a hypercube.  The first tesseract diagrams I ever saw were so confusing — they looked like lots of overlapped squares tied together with lines that didn’t make much sense.  I wondered, “Wouldn’t it be easier to understand a tesseract if I could see it rotating?”

Years later computers and I had both moved ahead to where I could generate the pictures you see in this post.  What I learned while doing that was that 4-D figures have two equators.  In four dimensions, it’s possible for something to rotate in two perpendicular directions at the same time.  Read on and please don’t mind my doggerel — it doesn’t bite.

line2c The LINE is just a single stroke,
a path from here to there.
Stretch it out beside itself
and you will have a SQUARE.
Where’s its face when it turns around?
Gone, ’cause its back’s not there.		 square2c
cube2c The CUBE’s a square
made thick, you see.
Length, breadth and depth
comprise a full 3-D.
Add yet a thickness more,
crosswise all to X, Y, Z.
A TESSERACT on a corner spins
but an XY-slice is all we see.		 tess2cxy
tess2czw But the axis, too, can rotate through
a path that’s drawn invisibly.
Four faces grow and shrink in place —
it’s hard to do that physically.
This tesseract is tumbling ’bout
two equators perpendicular.
Were I in such a state, I vow,
I’d be giddy, even sickular.		 tess4cxyzw

In the 4-D views, when one of the tesseract’s cubical faces appears to disappear into an adjacent face, what’s actually happening is that the face is sliding past the other face along that fourth dimension (which I called W because why not?)

You’re looking at a two-dimensional picture of the three-dimensional projection of a four-dimensional object as it moves in 5-space (X, Y, Z, W, and time — if it didn’t move in time then it couldn’t be spinning).

Next week — Herr Klein’s bottle, or rather flask, or rather surface.

~~ Rich Olcott

Dimensional venturing, Part 1 – What’s 4-D?

On By rolcottIn Cosmology, Mathematics: Dimensions, Uncategorized4 Comments

Whenever a science reporter uses the phrase “string theory,” it’s invariably accompanied by a sentence about tiny strings vibrating in 10 or 11 dimensions. Huh? How can you have more than three? And what does it really mean to say that that comix villain comes from the 4th dimension?  Actually, we live in many dimensions, though it’s not easy to visualize them all at once. Let’s get some practice.

Right now, you’re reading along a line, a one-dimensional path from left to right. Imagine a point drawing a straight line about a foot in front of you. Let that line just hang out there in the air, glowing a gentle green color, with one “edge” (the line itself) and two “corners” (its ends).

As you read down the page, you traverse a series of lines laid out next to each other in the two-dimensional plane of the page. Imagine your green line moving upward, leaving a plane of yellow sparkles behind it. Stop when you’ve got a sparkly yellow square in front of you showing its one face, four edges (one green, three yellow) and four corners (two green, two yellow). Let’s put some red paint on one of those yellow edges.Cube

Stack up enough printed pages and you’re got a 3-dimensional book. Imagine that nice yellow square moving away from you until you’ve got a friendly cube hanging out in the air. Our original line, the green edge, has produced a green face going into the distance. The red edge has built a pink face. All together, the cube has 8 corners, 12 edges and 6 faces. OK, now make your cube disappear.

But we’re not done yet. Time is a dimension. Consider that cube. Before you dreamed it up – nothing. Then suddenly a cube. Then nothing again. During the interval the cube was floating in front of you, the green line was tracing out a green face in time. The pink face was drawing a pink cube. The whole cube, from when it started to exist until it went away, traced out a four-dimensional figure called a tesseract, also called a 4-cube or hypercube. The tesseract was bounded by a cube at the beginning, six cubes while it existed (one from each face of the initial cube), and a cube at the end of its time, for a total of eight.

Just for grins, count up the faces, edges and corners for yourself.

But wait, there’s more. The tesseract doesn’t just sit there, it can spin. Being four-dimensional, it can spin in a surprising way. We’ll get to that next week.

~~ Rich Olcott