Category: Physics: Entropy and Thermodynamics

Rows, Columns And Freedom

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Geez, Sy. You know I hate equations. I was fine with the Phase Rule as an arithmetic thing but you’ve thrown so much algebra at me I’m flummoxed. How about something I can visualize?”

“Sorry, Vinnie, the algebra was just to show where the Rule came from. Application’s not in my bailiwick. Susan, it’s your turn.”

“Sure, Sy, this is Chemistry. Okay, Vinnie, what’s the Rule about?”

“Degrees of freedom, but I’m still not sure what that means. ‘Independent intensive variables’ doesn’t say much to me.”

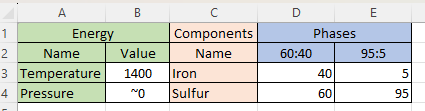
“Understandable, seeing as you don’t like equations. Visualize a spreadsheet. There’s an ‘Energy’ header over columns A and B. The second row reads ‘Name’ and ‘Value’ in those two columns. Then one row each for Temperature and Pressure.”

“This is more like it. Any numbers in the value column?”

“Not yet. They’ll be degrees of freedom, maybe. Next, ‘Components‘ in cell C1, ‘Name’ in C2 and then C rows, one for each component.”

“Do we care how much of each component?”

“Not yet.* Next visualize a multi‑column ‘Phases‘ header over one column for each phase. The second row names the phase. Below that there’s a row for each component. The whole array is for figuring how each component spreads across the phases assuming there’s enough of everything to reach equilibrium. With me?”

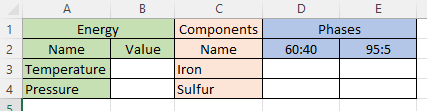
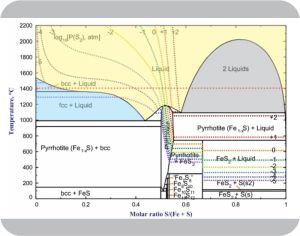
“A little ahead, I think. Take one of Kareem’s lava pools on Io, for instance. It’s got two components, iron and sulfur, and two molten phases, iron‑light 5:95 floating on top of iron‑heavy 60:40. Phase Rule says the freedom degrees is C–P+2=2–2+2, comes to 2 but that disagrees with the 6 open boxes I see.”

“But the boxes aren’t independent. Think of the interface between the two phases. One by one, atoms in each phase wander across to the other side. At equilibrium the wandering happens about as often in both directions.”

Adapted from Walder and Pelton
Click image to expand

“That’s your reversibility equilibrium.”

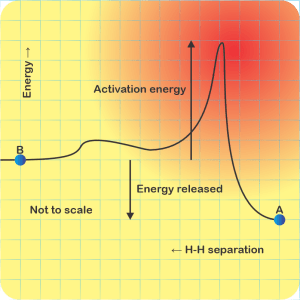
“Right, thermodynamics’ classic competition between energy and entropy — electronic energy holding things together against entropy flinging atoms everywhere. Pure iron’s a metallic electron soup that can accept a lot of sulfur without much disturbance to its energy configuration. That means sulfur’s enthalpy doesn’t differ much between the two environments and that allows easy sulfur traffic between the two phases. On the other hand, pure sulfur will accept only a little iron because iron disrupts sulfur‑sulfur moleular bonding. Steep energy barrier against iron atoms drifting into the 95:5 phase; low barrier to spitting them out. Kareem’s phase diagram for atmospheric pressure shows how things settle out for each temperature. There’s a neat equation for calculating the concentration ratios from the enthalpy differences, but you don’t like equations.”

“You’re right about that, Susan, but I smell weaseling in your temperature‑pressure dodge.”

Water’s phase diagram

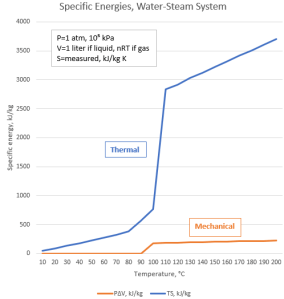
“Not really. You’ve read Sy’s posts about enthalpy’s internal energy, thermal and PV‑work components. Heat boosts entropy’s dominance and tinkers with the enthalpies.”

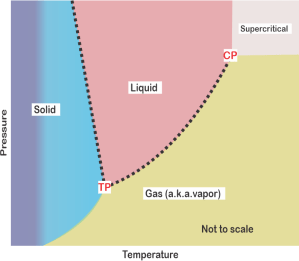
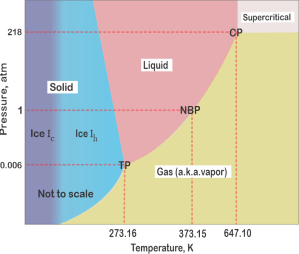
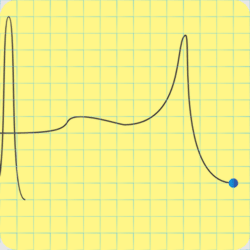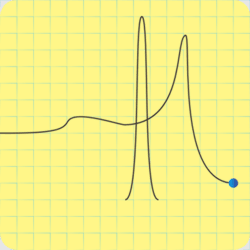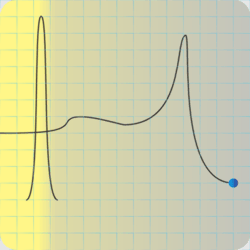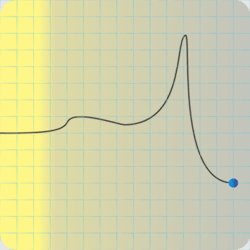
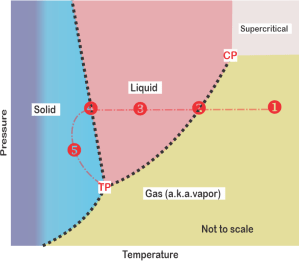
Meanwhile, I’ve been tapping Old Reliable’s screen. “I’m playing water games over here. Maybe this will help clarify the freedom. Water can be ice, liquid or vapor. At high temperature and pressure, the liquid and gas phases become a single phase we call supercritical. Here’s a sketch of water’s phase diagram. Only one component so C=1 … and a spreadsheet summarizing seven conditions.

“The first four are all at atmospheric pressure, starting at position 1 — just water vapor in a single phase so P=1, DF=2. We can change temperature and pressure independently within the phase boundaries. If we chill to point 2 liquid water condenses. If we stop there, on the boundary, we’re at equilibrium. We could change temperature and still be at equilibrium, but only if we change pressure just right so we stay on that dotted line. The temperature‑pressure linkage constraint leaves us only one degree of freedom — along the line.”

“Ah, 3 and 5 work the same way as 1 but for liquid and solid, and 4‘s like 2. The Fixed ones—?”

“One unique temperature‑pressure combination for each equilibrium. No freedoms left.”

  • * Given specific quantities of iron and sulfur, chemists can calculate equilibrium quantities for each phase. Susan assigned that as a homework problem once.

~ Rich Olcott

The Quest for Independents

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

The thing about Vinnie is, he’s always looking for the edges and loopholes. He’d make a good scientist or lawyer but he’s happy flying airplanes. “Guys, I heard a lot of dodging when you started talking about that Gibbs Rule. You said it only works when things are in equilibrium. That’s what Susan was talking about when she said Loki Lake on Io ain’t an equilibrium ’cause there’s stuff getting pumped in and going away so the equations don’t balance. I got that. But then you threw in some other excepts, like no biology or other kinds of work. What’s all that got to do with the phases and chemistry?”

“They’re different processes that drive a system away from equilibrium. Biology, for example. Every kind of life taps energy sources to maintain unstable structures. Proteins, for instance — chemically they’re totally unstable. Oxidation, random acid‑base reactions, lots of ways to degrade a protein molecule’s structure until its atoms wind up in carbon dioxide and nitrogen gas. Your cells, though, they continually burn your food for energy to protect old protein molecules or build new ones and DNA and bones and everything. I visualize someone riding a bicycle up a hillside of falling bowling balls, desperately fighting entropy just to keep upright.”

“Fearsome image, Susan, but it fits. From a Physics perspective, dumping in or extracting any kind of work disrupts any system that’s at equilibrium. The Phase Rule accounts for pressure-volume energy because that’s already part of enthalpy—”

“Wait, Sy, I don’t see pressure‑volume or even ‘PV‘ in
  ’degrees of freedom=components–phases+2‘.”

“That’s what the ‘2′ is about, Vinnie. If it weren’t for pressure‑volume energy, that two would be a one.”

“C’mon.”

“No, really. ‘Degrees of freedom’ counts the number of intensive properties that are independent of each other. Neither temperature nor pressure care about how much of something you’ve got, so they’re both intensive properties. Temperature’s always there so that’s one degree of freedom. If PV energy’s part of whatever process you’re looking at, then pressure comes into the Rule by way of the enthalpies we use to calculate equilibrium situations. I guess you could write the Rule as
  DF=C–P+1T+1PV.“

“That’s not the way we learned that in school, Sy. It was
  DF=C–P+1+N,
with ‘N’ counting the number of work modes — PV, gravitational, electrical, whatever fits the problem.”

“How would you do gravitational work on an ice cube, Kareem?”

“Wouldn’t be a cube, Vinnie, it’d be a parcel of Jupiter’s atmosphere caught in a kilometers‑high vertical windstream. Water ice, ammonia ice, ammonium polysulfide solids, all in a hydrogen‑helium medium. A complicated problem; whoever picks it up will have to account for gravity and pressure effects.”

“Come to think of it, the electric option is getting popular and Kareem’s iron‑sulfur system may be a big player. My Chemistry journals have carried a sudden flurry of papers about iron‑sulfur batteries as cheap, safe alternatives to lithium‑based designs for industry‑sized storage where low weight isn’t a consideration. Battery voltage is intensive, doesn’t care about size. Volt’s extensive ‘how much’ buddy is amps. Electrical work is volts times amps so it fits right in with the Rule if I write
  DF=C–P+1T+1PV+1VA
A voltage box with sulfur electrodes on one side and iron electrodes on the other would be way out of equilibrium.”

“But why components minus phases? Why not times? What if it comes out negative? What’d that even mean?”

Water’s phase diagram

“Fair questions, Vinnie. Degrees of freedom counts independent properties, right? You’d think the phases‑components contribution to DF would be P*C but no. The component percentages in C must total 100%. If you know all but one percentage, the last percentage isn’t independent. Same logic applies to the P phases. That leaves (C–1) and (P–1) independent variables. For the P phases P*C drops to P*(C–1) variables. But you also know that each component is in equilibrium across all phases. Each equilibrium reduces the count by one, for C*(P–1) reductions. Do the subtraction
  P*(C–1)–C*(P–1)=C–P
You’re left with only C–P quantities that can change without affecting other things. If the result’s negative it’ll constrain exactly that many other intensive variables, like with water’s triple point.”

~ Rich Olcott

Water Rites

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Vinnie pulls a chair over to our table, grabs some paper napkins for scribbling. “You guys know I hate equations, but this Phase Rule one is simple enough even I can play. It says ‘degrees of freedom’ equals ‘components’ minus ‘phases’ plus 2, right? Kareem’s phase diagram has a blue piece with a slush of iron crystals floating in an iron‑sulfur melt. There’s two components, iron and sulfur, two phases, crystals and melt, so the degrees come to 2–2+2=2 and that means we get to choose any two, you said intensive properties, to change. Do I got all that straight, tell me more about degrees and what’s intensive?”

Phase diagram for the iron:sulfur system
Adapted from Walder and Pelton
Click image to expand

“Good job, Vinnie, and good questions. Extensive properties are about how much. In Kareem’s experiment, he’s free to add iron or sulfur in whatever quantities he wants. By contrast, intensive properties don’t care about how much is there. The equilibrium melt’s iron:sulfur ratio stays between zero and one whatever the size of Kareem’s experiment. The ratio’s an intensive property. So are temperature and pressure. If he kept his experimental pressure constant but raised the temperature, I expect some of the crystals would dissolve. That’d lift the iron:sulfur ratio.”

“How about raising the pressure, Kareem?”

“I suspect that’d squeeze iron back into the crystalline mass, but I’ve not tried that so I don’t know. Different materials behave different ways. Raising the pressure on normal water ice melts it, which is why ice skates work.”

Susan suddenly pulls her tablet from her purse and starts fiddling with it.

“Fair enough. Okay, in your diagram’s top yellow piece where it’s all molten, there’s still 2 components but one phase so the Rule goes 2–1+2=3. You’re saying 3 degrees means you can choose whatever temperature, pressure and mix ratio you want and it’d still be molten.”

“You’ve got the idea, Vinnie. What I’m really interested in, though, is what happens when I add more components. To model Io’s lava pools I need to roll in oxygen and silicon from the surrounding rocks. I’m looking at a 4‑component situation which could have multiple phases and things are complicated”

Vinnie’s got that ‘gotcha’ glint in his eye. “Understood. But how about going in the other direction? If you’ve got only one component then you could have either 1–2+2=1 or 1–3+2=0. How do either of those make sense?”

Susan shows a display on her tablet. “As soon as Kareem mentioned ice I figured this phase diagram would come in handy. It’s for water — single component so there’s no variation along a component axis, just pressure and temperature.”

“Kareem had to read his chart to us. Now it’s your turn.”

“Of course. By convention, pressure’s on the y‑axis, temperature’s along the x‑axis. The pressure range is so wide that this chart uses a logarithmic scale which is why the distances look weird. Over there on the cold side, there’s two kinds of ice. Ice Ic has a cubic crystal structure. Warm it up past 240K and it converts to a hexagonal form, Ice Ih. That’s the usual variety that makes snowflakes.”

“TP!” <snirk, snirk>

“Cal, please. That’s water’s Triple Point, Vinnie’s 1–3+2=0 situation where all three phases are in equilibrium with each other so there’s no degrees of freedom. The solid‑liquid and liquid‑vapor boundaries are examples of Vinnie’s 1–2+2=1 condition — only one degree of freedom, which means that equilibrium temperature and pressure are tightly linked together. Squeeze on ice, its melting point drops, so we ice skate on a thin film of liquid water. Normal Boiling Point holds at standard atmospheric pressure but if you heat water while up on a balloon ride it may not get hot enough to hard‑boil those eggs you brought for the picnic.”

“What’s going on in the gray northeast corner?”

“CP‘s the Critical Point at the end of the 1–2+2=1 line. The liquid-vapor surface disappears. No gas or liquid in the container, just opalescent supercritical fog. There’s only one phase; temperature and pressure are independent. Beyond CP you’re in 1–1+2=2 territory.”

~ Rich Olcott

Surf Lake Loki? No, Thanks.

On By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Vinnie’s been eavesdropping (he’s good at that). “You guys said that these researcher teams looked at how iron and sulfur play together at a bunch of different temperature, pressures and blend ratios. That’s a pretty nice chart, the one that shows mix and temperature. Got one for pressure, like the near‑vacuum over Loki’s lava lake on Io?”

“Not to my knowledge, Vinnie. Of course I’m a lab chemist, not a theoretical astrogeochemist. Kareem’s phase diagram is for normal atmospheric pressure. I’d bet virtually all related lab work extends from there to the higher pressures down toward Earth’s center. Million‑atmosphere experiments are difficult — even just trying to figure out whether a microgram sample’s phase in a diamond anvil cell is solid or liquid. Right, Kareem?”

“Mm‑hm, but the computer work’s hard, too, Susan. We’ve got several suites of software packages for modeling whatever set of pressure-temperature-composition parameters you like. The problem is that the software needs relevant thermodynamic data from the pressure and temperature extremes like from those tough‑to‑do experiments. There’s been surprises when a material exhibited new phases no‑one had ever seen or measured before. Water’s common, right, but just within the past decade we may have discovered five new high‑pressure forms of ice.”

“May have?”

Artist’s concept of Loki Patera,
a lava lake on Jupiter’s moon Io
Credit: NASA/JPL-Caltech/SwRI/MSSS

“The academics are still arguing about each of them. Setting aside that problem, modeling Io’s low‑pressure environment is a challenge because it’s not a lab situation. Consider Cal’s pretty picture there. See those glowing patches all around the lava lake’s shore? They’re real. Juno‘s JIRAM instrument detected hot rings around Loki and nearly a dozen of its cousins. Such continual heat release tells us the lakes are being stirred or pumped somehow. Whatever delivers heat to the shore also must deliver some kind of hot iron‑sulfur phase to the cooler surface. That’ll separate out like slag in a steel furnace.”

“It’s worse than that, Kareem. Sulfur’s just under oxygen in the periodic table, so like oxygen it’s willing to be gaseous S2. Churned‑up hot lava can’t help but give off sulfur vapor that the models will have to account for.”

I cut in. “It’s worse than that, Susan. I’ve written about Jupiter’s crazy magnetic field, off‑center and the strongest of any planet. Io’s the closest large moon to Jupiter, deep in that field. Sulfur molecules run away from a magnetic field; free sulfur atoms dive into one. Either way, if you’re some sulfur species floating above a lava lake when Jupiter’s field sweeps past, you won’t be hanging around that lake for long. Most likely, you’ll join the parade across the Io‑to‑Jupiter flux tube bridge.”

Susan chortles. “Obviously not an equilibrium. It’s a steady state!”

“Huh?” from everyone. Cal gives her, “Steady state?”

“Chemical equilibrium is when a reaction and its reverse go at equal rates, right, so the overall composition doesn’t change. That’s the opposite of situations where there’s a forward reaction but for some reason the products don’t get a chance to back‑react. Classic case is precipitation, say when you bubble smelly H2S gas through a solution that may contain lead ions. If there’s lead in there you get a black lead sulfide sediment that’s so insoluble there’s no re‑dissolve. Picture an industrial vat with lead‑contaminated waste water coming in one pipe and H2S gas bubbling in from another. If you adjust the flow rates right, all the lead’s stripped out, there’s no residual stink in the effluent water and the net content of the vat doesn’t change. That’s a steady state.”

“What’s that got to do with Loki’s lake?”

“Sulfur vapors come off it and those glowing rings tell us it’s giving off heat. It’s just sitting there not getting hotter and probably not changing much in composition. There’s got to be sulfur and heat inflow to make up for the outflow. The lake’s in a steady state, not an equilibrium. Thermodynamic calculations like Gibbs’ phase rule can’t tell you anything about the lake’s composition because that depends on the kinetics — how fast magma comes in, how fast heat and sulfur go out. Kareem’s phase diagram just doesn’t apply.”

~ Rich Olcott

Phases And Changes

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Okay, so the yellow part of your graph is molten iron and sulfur, Kareem. What’s with all the complicated stuff going on in the bottom half?”

“It’s not a graph, Cal, it’s a phase diagram. Mmm… what do you think a phase is?”

“What we learned in school — solid, liquid, gas.”

“Sorry, no. Those are states of matter. Water can be in the solid state, that’s ice, or in the liquid state like in my coffee cup here, or in the gaseous state, that’d be water vapor. Phase is a tighter notion. By definition, it’s an instance of matter in a particular state where the same chemical and physical properties hold at every point. Diamond and graphite, for example, are two different phases of solid carbon.”

“Like when Superman squeezes a lump of coal into a diamond?”

“Mm-hm. Come to think of it, Cal, have you ever wondered why the diamonds come out as faceted gems instead of a mold of the inside of his fist? But you’ve got the idea — same material, both in the solid state but in different phases. Anyway, in this diagram each bordered region represents a phase.”

Phase diagram for the iron:sulfur system
Adapted from Walder and Pelton

“It’s more complicated that that, Kareem. If you look close, each region is actually a mixture of phases. The blue region, for instance, has parts labeled ‘bcc+Liquid’ and ‘fcc+Liquid’. Both ‘bcc’ and ‘fcc’ are crystalline forms of pure iron. Each blue region is really a slush of iron crystals floating in a melt with just enough sulfur to make up the indicated sulfur:iron composition. That line at 1380°C separates conditions where you have one 2‑phase mix or the other.”

“Point taken, Susan. Face it, if region’s not just a straight vertical line then it must enclose a range of compositions. If it’s not strictly molten it must be some mix of at least two separate more‑or‑less pure components. That cool‑temperature mess around 50:50 composition is a jumble when you look at micro sections of a sample that didn’t cool perfectly and they never can. The diagram’s a high‑level look at equilibrium behaviors.”

“Equilibrium?”

“‘Equi–librium’ came from the Latin ‘equal weight’ for a two-pan balance when the beam was perfectly level. The chemists abstracted the idea to refer to a reaction going both ways at the same rate.”

“Can it do that, Susan?”

“Many can, Cal. Say you’ve got a beaker holding some dilute acetic acid and you bubble in some ammonia gas. The two react to produce ammonium ions and acetate ions. But the reaction doesn’t go all the way. Sometimes an ammonium ion and an acetate ion react to produce ammonia and acetic acid. We write the equation with a double arrow to show both directions. Sooner or later you get equally many molecules reacting in each direction and that’s a chemical equilibrium. It looks like nothing’s changing in there but actually a lot’s going on at the molecular level. Given the reactant and product enthalpies Sy’s been banging on about, we can predict how much of each substance will be in the reaction vessel when things settle down.”

“Banging on, indeed. You’re disrespecting a major triumph of 19th‑Century science. Before Gibbs and Helmholtz, industrial chemists had to depend on rules of thumb to figure reaction yields. Now they just look up the enthalpies and they’ can make good estimates. Gibbs even came up with his famous phase rule.”

“You’re gonna tell us, right?”

“Try to stop him.”

“The Gibbs Rule applies to systems in equilibrium where there’s nothing going on that’s biological or involves electromagnetic or gravitational work. Under those restrictions, there’s a limit to how things can vary. According to the rule, a system’s degrees of freedom equals the number of chemical components, minus the number of phases, plus 2. In each blue range, for instance, iron and sulfur make 2 components, minus 2 phases, plus 2, that’s 2 degrees of freedom.”

“So?”

“Composition, temperature and pressure are three intensive variables that you might vary in an experiment. Pick any two, the third is locked in by thermodynamics. Set temperature and pressure, thermodynamics sets the composition.”

~ Rich Olcott

A Lazy Summer Day at 1400°C

On By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Susan Kim and Kareem are supervising while Cal mounts a new poster in the place of honor behind his cash register. “A little higher on the left, Cal.”

“How’s this, Susan? Hey, Sy, get over here and see this. Ain’t it a beaut?”

“Nice, Cal. What’s it supposed to be? Is that Jupiter in the background?”

“Yeah, Jupiter all right. Foreground is supposed to be a particular spot on its moon Io. They think it’s a lake of molten sulfur!”

“No way, from that picture at least! I’ve seen molten sulfur. It goes from pale yellow to dark red as you heat it up, but never black like that.”

“It’s not going to be lab-pure sulfur, Susan. This is out there in the wild so it’s going to be loaded with other stuff, especially iron. But the molten sulfur I’ve seen in volcanoes is usually burning with a blue flame. I guess the artist left that out.”

“No oxygen to burn it with, Kareem. Why did you mention iron in particular?”

“Yeah, this article I took the image from says that lake’s at 1400°C. I thought blast furnaces ran hotter than that.”

I’ve been looking things up on Old Reliable. “They do, Cal, typically peaking near 2000°C.”

“So if this lake has iron in it, why isn’t the iron solid?”

“Same answer as I gave to Susan, Cal. The iron’s not pure, either. Mixtures generally melt or freeze at lower temperatures than their pure components. Sy would probably start an entropy lecture—”

“I would.”

“But I’m a geologist. Earth is about ⅓ iron. That’s mixed in with about 10% as much sulfur, mostly in the core where pressures and temperatures are immense. We want to understand conditions down there so we’ve spent tons of lab time and computer time to determine how various iron‑sulfur mixtures behave at different temperatures and pressures. It’s complicated.” <brings up an image on his phone> “Here’s what we call the system’s phase diagram.”

“You’re going to have to read that to us.”

Adapted from Walder and Pelton
Click image to expand

“I expected to. Temperature increases along the y‑axis. Loki’s temp is at the dotted red line. Left‑to‑right we’ve got increasing sulfur:iron ratios — pure iron on the left, pure sulfur on the right. The idea is, pick a temperature and a mix ratio. The phase diagram tells you what form or forms dominate. The yellow area, for instance, is liquid — molten stuff with each kind of atom moving around randomly.”

“What’s the ‘bcc’ and ‘fcc’ about?”

“I was going to get to that. They’re abbreviations for ‘body‑centered cubic’ and ‘face‑centered cubic’, two different crystalline forms of iron. The fcc form dominates below that horizontal line at about 1380°C, converts to bcc above that temperature. Pure bcc freezes at about 1540°C, but add some sulfur to the molten material and you drive that freezing temperature down along the blue‑yellow boundary.”

“And the gray area?”

“Always a fun thing to explain. It’s basically a no‑go zone. Take the point at 1400°C and 80:20 sulfur:iron, for instance. The line running through the gray zone along those red dots, we call it a tie line, skips from 60:40 to 95:5, right? That tells you the 60:40 mix doesn’t accept additional sulfur. The extra part of the 80:20 total squeezes out as a separate 95:5 phase. Sulfur’s less dense than iron so the molten 95:5 will be floating on top of the 60:40. Two liquids but they’re like oil and water. If you want a uniform 80:20 liquid you have to shorten the tie line by raising the temp above 2000°C.”

“All that’s theory. Is there evidence to back it up?”

“Indeed, Sy, now that Juno‘s up there taking pictures. When the spacecraft rounded Io last February JunoCam caught several specular reflections of sunlight just like it had bounced off mirrors. At first the researchers suspected volcanic glass but the locations matched Loki and other hot volcanic calderas. The popular science press can say ‘sulfur lakes’ but NASA’s being cagey, saying ‘lava‘ — composition’s probably somewhere between 10:90 and 60:40 but we don’t know.”

Artist’s concept of Loki Patera,
a lava lake on Jupiter’s moon Io
Credit: NASA/JPL-Caltech/SwRI/MSSS

~ Rich Olcott

A Sublime Moment

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, Uncategorized1 Comment

It’s either late Winter or early Spring, trying to make up its mind. Either way, today’s lakeside walk is calm until I get to the parking lot and there he is, all bundled up and glaring at a huge pile of snow. “Morning, Mr Feder. You look even more out of sorts than usual. Why so irate?”

“The city’s dump truck buried my car in that stuff.”

“Your car’s under that? But there’s a sign saying not to park in that spot when there’s a snow event.”

“Yeah, yeah. Back on Fort Lee we figure the city just puts up signs like that to remind us we pay taxes. I’ll park where I want to. Freedom!”

“I’m beginning to understand you better, Mr Feder. Got a spare shovel? I can help you dig out.”

“My car shovel’s in the car, of course. I got another one at home for the sidewalk.”

I notice something, move over for a better view. “Step over here and look close just above the top of the pile where the sunlight’s hitting it.”

“Smoke! My car’s burning up under there!”

“No, no, something much more interesting. You’re looking at something that I’ve seen only a couple of times so you’re a lucky man. That’s steam, or it would be steam at a slightly higher temperature. What you’re looking at is distilled snow. See the sparkles from ice crystals in that cloud? Beautiful. Takes a very special set of circumstances to make that happen.”

“I’d rather be lucky in the casino. What’s so special?”

“The air has to be still, absolutely no breeze to sweep floating water molecules away from the pile. Temperature below freezing but not too much. Humidity at the saturation point for that temperature. Bright sun shining on snow that’s a bit dirty.”

“Dirty’s good?”

“In this case. Here’s the sequence. Snow is water molecules locked into a crystalline structure, right? Most of them are bonded to neighbors top, bottom and every direction. The molecules on the surface don’t have as many neighbors, right, so they’re not bonded as tightly. So along comes sunlight, not only visible light but also infrared radiation—”

“Infrared’s light, too?”

“Mm-hm, just colors we can’t see. Turns out because of quantum, infrared light photons are even more effective than visible light photons when it comes to breaking water molecules away from their neighbors. So a top molecule, I’ll call it Topper, escapes its snow crystal to float around in the air. Going from solid directly to free-floating gas molecules, we call that sublimation. Going the other way is deposition. Humidity’s at saturation, right, so pretty soon Topper runs into another water molecule and they bond together.”

<sarcasm, laid on heavily> “And they make a cute little snow crystal.”

“Not so fast. With only two molecules in the structure, you can’t call it either solid or liquid but it does grow by adding on more molecules. Thing is, every molecule they encounter gives up some heat energy as it ties down. If the weather’s colder than it is here, that’s not enough to overcome the surrounding chill. The blob winds up solid, falls back down onto the pile. If it’s just a tad warmer you get a liquid blob that warms the sphere of air around it just enough to float gently upwards—”

“Like a balloon, I got the picture.”

“Floats up briefly. It doesn’t get up far before the surrounding chill draws out that heat and wins again. Not so brief when there’s a little dirt in there.”

“The dirt floats?”

“Of course not. The dirt’s down in the snow pile, but it’s dark and absorbs more sunlight energy than snow crystals do. What the dirt does is, it tilts the playing field. Heat coming from the dirt particles increases the molecular break‑free rate and there’s more blobs. It also warms the air around the blobs and floats them high enough to form this sparkling cloud we can see and enjoy.”

“You can enjoy it. I’m seeing my car all covered over and that’s not improving my mood.”

“Better head home for that shovel, Mr Feder. The snow dumper’s coming back with another load.”

~ Rich Olcott

Xanax For Molecules

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Vinnie plops down by our table at Cal’s Coffee. “Hi, guys. Glad you’re both here. Susan, Sy here says you’re an RDX expert so I got a question.”

“Not an expert, Vinnie, it’s just one of a series of compounds in one of my projects. What’s your question?”

“How come the stuff is so touchy but it’s not touchy? You can shoot a bullet into a lump of it, nothing happens, but set off a detonator next to it and WHAMO! Why do we need a detonator, and what’s in one anyway?”

“Sy, what sets off an H‑bomb?”

“An A‑bomb. You need a lot of energy in a confined region to crowd those protons enough that they fuse.”

“And what sets off an A‑bomb?”

“Hey I know that one, Susan, I saw the Oppenheimer movie. You need some kind of explosives going off just right to cram two chunks of plutonium together real fast so they do the BANG! thing instead of just melting. Wait! I see where you’re going — little explosions trigger big explosions, right?”

“Bravo! You’ve got the idea behind activation energy.”

“Geez, another kind of energy?”

“Yes and no, Vinnie. Enthalpy and its cousins are about the net change when something happens. We can use them to predict how a complex reaction will settle down, but they don’t tell us much about the kinetics, how fast things will happen. Think for a minute about those H‑bomb hydrogen atoms. What prevents them from fusing?”

“I guess under normal conditions they’re too far apart and even when they get close their electron clouds push against each other.”

<Sketching on a paper napkin> “Fair enough. Okay, here’s what the potential energy curve looks like, sorta. There’s hydrogen atom A over there at the right-hand end of the curve. B‘s a second hydrogen on the left and heading inwards. With me?”

“So far.”

“Right. Now, B comes roaring in with some amount of kinetic energy and hits the potential energy bump where those electron clouds overlap. If it has enough kinetic energy to overcome that barrier, it keeps on going. Otherwise it bounces back with the kinetic energy it had maybe minus some that A picked up in the recoil.”

“So the first barrier is the electron‑electron repulsion, but the potential dips in the middle where the clouds merge and that’s where molecules happen.”

“Right, Sy. But then there’s the second barrier as B‘s positive charge encounters A‘s. Inverse‑square law and all that, it’s an enormous hurdle. Visualize lots of Bs with different kinetic energies running up against that wall again and again until finally, if the pressure’s high enough, one gets past and the fusion releases more energy than the winning B had originally. The higher the wall, the fewer Bs hit As per unit time and the slower the reaction.”

“Looking at the before‑and‑afters, the reaction only happens if energy’s released, but how fast it goes is that barrier’s fault.”

“Perfect, Vinnie. Take RDX, for example. You’re right, it’s touchy. If you’ve got the pure stuff, never look at it cross‑eyed unless you’re behind a blast shield. Lots of energy released, very low energy of activation.”

“But like I said, you can shoot a gun at it, no effect.”

“That wasn’t pure RDX, it was probably some version of C‑4.”

“Yeah, C‑4, don’t know any of the details.”

“C‑4’s explosive is RDX, but it’s also got some plasticizer for that putty consistency, and a phlegmatizer. I love that word.”

“Phlegmatizer? That’s a new one for me.”

“It’s an additive to keep the explosive calm — phlegmatic, get it? — until it gets excited on purpose, which is the detonator’s job.” <scribbling on a stack of paper napkins> “Okay, here’s that same activation energy curve, an RDX particle on the right, and an incoming shock wave. The gray region is the phlegmatizer, usually paraffin or a heavy oil. Think of it as a shock absorber, absorbing or deflecting the shockwave before it can activate the explosive. A detonator’s designed to activate and erupt so quickly that its shock peak arrives before the phlegmatizer can spread it out.”

“Like they say, timing is everything.”

~ Rich Olcott

Tightening Up Fast And Loose

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Cal brings out a fresh batch of scones. He’s tonging them onto the racks when I suddenly get a whiff of mocha latte. I glance back and there’s Susan Kim, grinning at me. “Hi, Sy. Grab your scone and a table. I have a bone to pick with you.”

A few moments later we’re seated. Cal’s coffee’s especially smooth today. “Okay, what’s the bone?”

“You’re playing fast and loose with your enthalpy definition. Yes, there’s change in temperature times entropy, enthalpy’s thermal component, and an expansion‑contraction component you called pressure‑volume. But it’s just sloppy to call what’s left ‘the chemical portion.’ What it is, really, is the combination of every other kind of energy something has that some process could extract. Chemical reactions are just one piece.”

“Strong words, coming from a chemist. What else should be packed in there?”

“Radioactivity, for one. It’s a heat source that doesn’t depend on chemical reactions. Atom for atom, a nuclear disintegration can yield millions of times more energy than a chemical reaction does. Trouble is, radioactive atoms only break down when they feel like it so the energy’s all random heat. I’m sure there’s a bunch of other non‑chemical ways to increase something’s apparent enthalpy.”

“Hmm. Challenge accepted. … It’s all about which process will extract some kind of energy from your something. How about the something’s a tightly‑wound spring? No, wait, that’s chemical, because the energy’s stored in stretched metal‑metal bonds.”

“No, I’ll accept spring tension because there’s no change in chemical composition during the unwind process. What’s another one?”

“Ah. Easy. Kinetic energy if the something’s flying through the air to hit something else.”

“Now you’re cooking. Gravitational potential energy if it’s falling down. Oh, suppose it’s magnetized and goes through a conductive loop on the way down?”

“Nope, doesn’t count. The object’s kinetic energy would produce a jolt of electrical potential in the loop, but it’s own magnetization wouldn’t change. Nice, that distinction sharpens the point — what you count as enthalpy’s third component depends on which change process you’re talking about. If there’s no chemical change, then the chemical part of the internal component of the enthalpy change is zero. In the early days of thermodynamics, for instance, everyone was working on steam. Water may corrode your equipment over the long term, but otherwise it’s just hot water molecules becoming not‑as‑hot water molecules and there’s no change in internal energy. The only energy terms you have to think about are pressure‑volume and temperature‑entropy. That’s why they defined it that way.”

“Which one wins?”

“Hmm?”

“You’ve pared enthalpy changes down to just two kinds of energy. I’ve got to wonder, which one has the bigger contribution?”

<pulls up a display on Old Reliable> “This is just for the water‑steam system, mind you. Vinnie was surprised. It’s all based on specific heat measurements so visualize one kilogram of liquid water.”

“A liter, right.”

“The line labeled ‘Mechanical’ is the amount of energy you’d get by expanding that kilogram from 0°C up to the temperatures laid out on the x‑axis. No significant expansion up near boiling temperature, then it follows the Ideal Gas Law, PV=nRT. At atmospheric pressure and in this temperature range the expansion relative to 0°C runs about 200 kilojoules per kilogram.”

“And the ‘Thermal’ line?”

“That’s lab‑measured heat capacity values I pulled from the CRC Handbook, each multiplied by the corresponding temperature in kelvins. That’s the amount of energy our kilogram of water molecules holds just by being at the temperature it’s at. The gas makes a nice straight line, at least in the range before heat shatters the molecules.”

“That’s what, fifteen or sixteen times more energy than the mechanical part? Wow! You know, back in Physical Chemistry class they just threw around lots of confusing thermodynamics formulas but never put numbers to them. I had no idea the entropy effect could just swamp whatever else.”

“Numbers do make a difference.”

“This clarifies something I didn’t understand back then. Entropy’s about randomness, right, and a gas molecule can be in more locations in a large volume than in a small one. V=nRT/P says volume rises linearly with temperature and that’s the linear rise in your chart.”

~ Rich Olcott

The Little Engine That Cooled

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Chemical potential energy is something else, Sy. You’ve got like this lump of putty just sitting there and suddenly WHAMO! Kinetic energy all over the place.”

“Sounds like you’ve been playing with explosives, Vinnie.”

“Sorta. Some of the Specials down at the base let me watch a couple of their C-4 practice shots. You know anything about C-4?”

“A little, like what it’s made of. Susan Kim’s interested in the main ingredient for some chemical reason. She calls it RDX, drew me a picture of it once. Nice symmetrical molecule loaded with nitrogen and carbon atoms just itching to fly away as a dozen separate gas molecules. Funny, how such violent stuff can be so relaxed until just the right thing sets it off. Like some people I know.”

Combustion of an RDX molecule

“Ouch. Yeah, it happens, but I’m mellowing, okay? A dozen fragments per molecule, got it. Hey, what chemical is ‘NOx‘?”

“Could be nitrous oxide N2O, or nitric oxide NO, or some combination depending, which is why there’s no number in the equation in front of oxygen’s O2. Combustion is messy.”

“Yeah, enthalpy all over the place! Those separate gas molecules spread out to a way bigger volume than the solid molecule used up. Lotsa pressure‑volume work there, right?”

“True, but gas expansion’s only one factor in an RDX discharge. Did the guys at the base mention that if you detonate that putty when it’s spread thin it can burn through an I‑beam?”

“So there’s heat, too. Can’t be much stacked up against the expansion.”

“Don’t be so sure. I’m not up on RDX thermochemistry. I never asked Susan and I don’t know whether she or anyone knows the breakout. It’s hard to do a precision measurement on an explosion, even if you do it in milligram quantities. I’ve got a good substitute for that, though. Water’s way simpler and much more thoroughly studied.”

“How is water a substitute? It doesn’t explode.”

“True, but it boils. No changes in molecular bonding, so enthalpy’s chemical part isn’t a factor. Carnot taught us to figure the pressure‑volume and thermal parts separately. Suppose you load a liter of water into a cylinder‑piston arrangement that stays at one atmosphere pressure. Get it up to boiling temperature then measure the energy input while the water boils away. The water absorbs energy while it turns to steam, right, even though there’s no change in temperature.”

“It stays at 212°?”

“212°F is 100°C or 373 K, stays steady provided the pressure stays at one atmosphere, 14.7 psi or 101325 pascals, whichever units you want to use. Pressure and temperature work together when it comes to phase changes. Anyway, the only way your rig can maintain that exact pressure is to do some kind of work, lifting a weight or something, until the cylinder’s final volume above the piston is 1705 liters. That’ll be 172 kilojoules of useful work.”

“Big cylinder.”

“Granted, but we supposed a liter of water. Scale the equipment to handle just a milliliter of water and the swept volume’s down to 1.7 liters. Neat how the metric system works. But now you’ve got a design decision to make. You can release the steam with a loud CHUFF that carries away 92% of the energy you put into it—”

“That’s no good.”

“— or you can run it through a condenser that preheats the feed water for the next cycle. Saves a lot of fuel that way.”

“That’d be my choice.”

“Mm-hm. That was Watt’s crucial improvement on Newcomen’s design. Funny thing, though. Both guys are credited with ‘inventing the steam engine’ but neither one built a device like the engines we’re used to, ones that develop power by pushing on a piston. The big demand in their day was pumping water out of mine shafts. Newcomen and Watt built vacuum gadgets.”

Watt’s steam pumping engine

“I had a well once. You can’t pull water up more than about 35 feet.”

“Right. Vacuum pumping is limited. Unfortunately, so was manufacturing technology in Watt’s time. Making a piston and cylinder that would fit together efficiently over a wide temperature range was a big challenge.”

“Their engines sucked, huh?”

~ Rich Olcott