atomic orbitals – Hard Science Ain't Hard

“Okay, Sy, what’s your third solution?”

“Solution to what, Susan?”

“These harmonic thingies. They’re about angles so it makes sense to chart them in polar or spherical coordinates, but when they take on negative values the radius goes the wrong way. You said one solution was to chart the negatives in a different color. That’s confusing, though. Another solution is to square all the values to get everything into positive territory. That’s okay for chemists like me because the peaks and nodes we care about stay in the same places. What’s the third option?”

“One that gets to why these ‘harmonic thingies’ are interesting at all. When Juno‘s orbiting Jupiter, does it feel each of Kaspi’s J_n shapes individually?”

“No, of course not, she just reacts to how they all add togethherrr … Oh! So you’re saying we can handle negative values from one harmonic by adding it to another one that’s more positive and plotting the combination.”

<pointing to paper napkin> “Bingo! Remember this linear plot of J₂ where I colored its negative section pink?” <pointing to display on Old Reliable> “When you multiply J₂ by C₀ you get S₂₂₀. I added that to four helpings of S_n00 to get this combination.”

“Ah, that negative region in S₂₂₀‘s middle shaves back the equator on S_n00‘s sphere while the positive part adds bumps top and bottom.” <Susan gives me the side‑eye> “Why’d you pick that 4‑to‑1 ratio, and what’s with those n subscripts instead of numbers?”

“Getting a little ahead of myself. For the moment let’s concentrate on Juno‘s experience with Jupiter’s gravity. One reason I chose that ratio was that it’s pretty easy to see in the picture. In real cases the physical system determines the ratios. Kaspi’s team derived their ratios experimentally. They used math to fit a model to Juno‘s very slightly wobbly orbit. Their model of Jupiter’s gravity field started from the spherical J₀ shape. They tweaked that by adding different ratios of J₂ through J₄₀, adjusting the ratios until the model’s total gravity field predicted an orbit that matched the real‑world one. J₂‘s share was about 15 parts per thousand but most of the rest contributed less than a part per million. Jupiter probably uses multiple mass blobs to make the J₂ shape. The point is, the planet’s really a mess but we can analyze the mess in terms of the harmonics.”

“So that’s how you drew what Cal called your wiggle-waggles — you followed Kaski’s J_n recipe and then added some constant to push the polar plot out far enough that the negatives didn’t poke out the wrong side. That constant — what value did you use and why that one?”

“That’s exactly what I did do, Cathleen. Frankly, I don’t even remember what constant I added, just something that was big enough to make the negatives behave nicely, not so large that the peaks vanished by comparison. Calibrating accurately to Jupiter’s J₀ would shrink the peaks down to parts‑per‑thousand invisibility. After all, I was more concerned with peak position than peak size.”

“Now we’re back to your 4‑to‑1 ratio. Was that arbitrary, too?”

“No, it wasn’t, Susan. Would it have been closer to Chemistry if I’d labeled that figure as 1s²2s²2p¹?”

“Two electrons in the 1s‑shell, two in the 2s‑shell plus one 2p electron … that’s a boron atom? But you’re showing only one radial shell, not two separate ones.”

“True, but that’s to make another point. There isn’t an electron in the 1s shell, or even a pair of them nicely staying on opposite sides. The atom’s charge, all five electrons‑worth of it, is smeared out as a wave pattern across the entire structure. The S_n00 pattern captures everything that’s spherical. The S₂₂₀ pattern gets what’s left.”

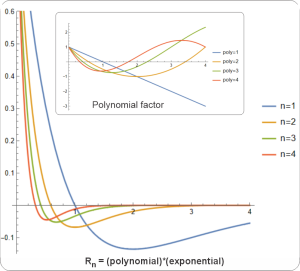
“But what about the radial nodes? Isn’t that the difference between 1s and 2s, that 2s has a node?”

“Oh there are nodes, alright, but they don’t have much effect. Each radial harmonic is the product of two factors — a polynomial and an exponential. The exponential part squeezes the polynomial so hard that adjacent peaks and valleys are barely bumps and dents.”

“So Jupiter and atoms use the same math, huh?”

“So does the Sun.”

~~ Rich Olcott

I’m nursing my usual mug of eye‑opener in Cal’s Coffee Shop when astronomer Cathleen and chemist Susan chatter in and head for my table. Susan fires the first volley.

“Sy, those spherical harmonics you’ve posted don’t look anything like the atomic orbitals in my Chem text. Shouldn’t they?”
”How do you add and multiply shapes together?”
”What does the result even mean?”
”And what was that about solar seismology?”

“Whoa, have you guys taken interrogation lessons from Mr Feder? One at a time, please. Let’s start with the basics.” <sketching on a paper napkin> “For example, the J₂ zonal harmonic depends only on the latitude, not on the longitude or the distance from the center, so whatever it does encircles the axis. Starting at the north pole and swinging down to the south pole, the blue line shows how J₂ varies from 1.0 down to some negative decimal. At any latitude, whatever else is going on will be multiplied by the local value of J₂.”

“The maximum is 1.0, huh? Something multiplied by a number less than 1 becomes even smaller. But what happens where J₂ is zero? Or goes negative?”

“Wherever J_n‘s zero you’re multiplying by zero which makes that location a node. Furthermore, the zero extends along its latitude all around the sphere so the node’s a ring. J₂‘s negative value range does just what you’d expect it to — multiply by the magnitude but flip the product’s sign. No real problem with that, but can you see the problem in drawing a polar graph of it?”

“Sure. The radius in a polar graph starts from zero at the center. A negative radius wouldn’t make sense mixed in with positives in the opposite direction.”

“Well it can, Cathleen, but you need to label it properly, make the negative region a different color or something. There are other ways to handle the problem. The most common is to square everything.” <another paper napkin> “That makes all the values positive.”

“But squaring a magnitude less than 1 makes it an even smaller multiplier.”

“That does distort the shapes a bit but it has absolutely no effect on where the nodes are. ’Nothin’ times nothin’ is nothin’,’ like the song says. Many of the Chem text orbital illustrations I’ve seen emphasize the peaks and nodes. That’s exactly what you’d get from a square‑everything approach. Makes sense in a quantum context, because the squared functions model electron charge distributions.”

“Thanks for the nod, Sy. We chemists care about charge peaks and nodes around atoms because they control molecular structures. Chemical bonds and reactions tend to localize near those places.”

“I aim for fairness, Susan. There is another way to handle a negative radius but it needs more context to look reasonable. Meanwhile, we’ve established that at any given latitude each J_n is just a number so let’s look at longitudes.” <a third paper napkin> “Here’s the first two sectorial harmonics plotted out in linear coordinates.”

“Looks familiar.”

“Mm‑hm. Similar principles, except that we’re looking at a full circle and the value at 360° must match the value at 0°. That’s why C_m always has an even node count — with an odd number you’d have -1 facing +1 and that’s not stable. In polar coordinates,” <the fourth paper napkin> “it’s like you’re looking down at the north pole. C₀ says ‘no directional dependence,’ but C₁ plays favorites. By the way, see how C₁‘s negative radii in the 90°‑270° range flip direction to cover up the positives?”

“Ah, I see where you’re going, Sy. Each of these harmonics has a numeric value at each angle around the center. You’re going to tell us that we can multiply the shapes by multiplying their values point by point, one for each latitude for a J and each longitude for a C.”

“You’re way ahead of me as usual, Cathleen. You with us, Susan?”

“Oh, yes. In my head I multiplied your J₂ by C₀ and got a p_z orbital.”

“I’m impressed.”
”Me, too.”

“Oh, I didn’t do it numerically. I just followed the nodes. J₂ has two latitude nodes, C₀ has no longitude nodes. There it is, easy‑peasy.”

~~ Rich Olcott

Hard Science Ain't Hard

Tag: atomic orbitals

Jupiter And The Atoms

Shapes And Numbers