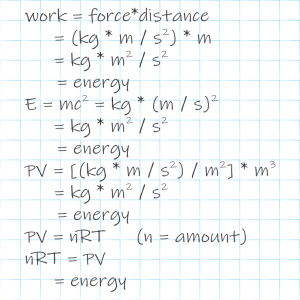Tag: Einstein

A Cosmological Horse Race

On By rolcottIn Astronomy: Multi-messenger, Cosmology, Physics: Einstein, Physics: Electromagnetism, UncategorizedLeave a comment

A crisp Fall day, perfect for a brisk walk around the park. I see why the geese are huddled at the center of the lake — Mr Feder, not their best friend, is on patrol again. Then he spots me. “Hey, Moire, I gotta question!”

“Of course you do, Mr Feder. What is it?”

“Some guy on TV said Einstein proved gravity goes at the speed of light and if the Sun suddenly went away it’d take eight minutes before we went flying off into space. Did Einstein really say that? Why’d he say that? Was the TV guy right? And what would us flying across space feel like?”

“I’ll say this, Mr Feder, you’re true to form. Let’s see… Einstein didn’t quite prove it, the TV fellow was right, and we’d notice being cold and in the dark well before we’d notice we’d left orbit. As to why, that’s a longer story. Walk along with me.”

“Okay, but not too fast. What’s not quite about Einstein’s proving?”

“Physicists like proofs that use dependable mathematical methods to get from experimentally-tested principles, like conservation of energy, to some result they can trust. We’ve been that way since Galileo used experiments to overturn Aristotle’s pure‑thought methodology. When Einstein linked gravity to light the linkage was more like poetry. Beautiful poetry, though.”

“What’s so beautiful about something like that?”

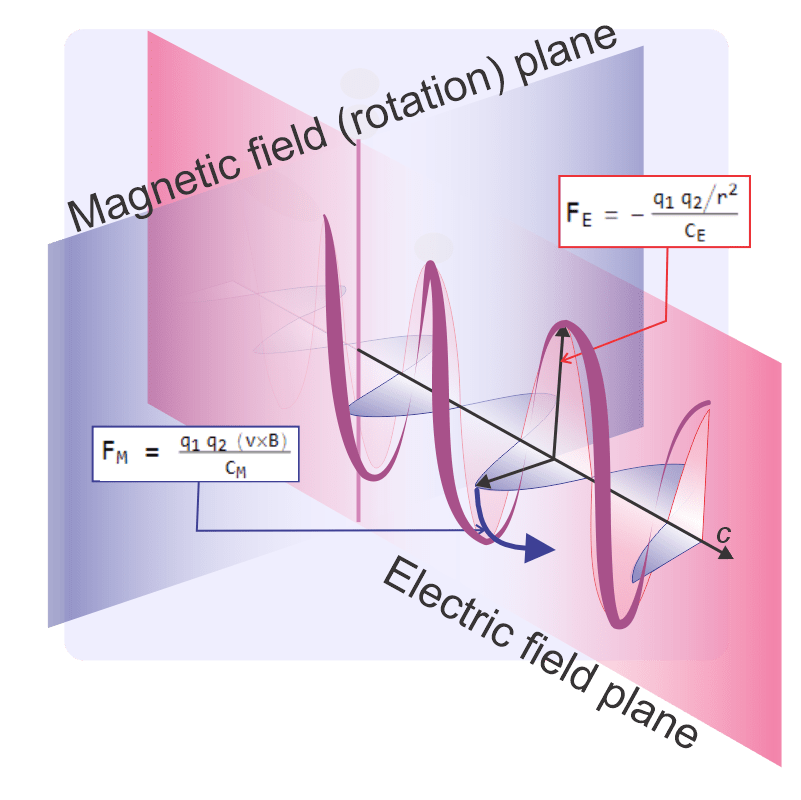
“All the rhymes, Mr Feder, all the rhymes. Both gravity and light get less intense with the square of the distance. Gravity and light have the same kinds of symmetries—”

“What the heck does that mean?”

“If an object or system has symmetry, you can execute certain operations on it yet make no apparent difference. Rotate a square by 90° and it looks just the same. Gravity and light both have spherical symmetry. At a given distance from a source, the field intensity’s the same no matter what direction you are from the source. Because of other symmetries they both obey conservation of momentum and conservation of energy. In the late 1890s researchers found Lorentz symmetry in Maxwell’s equations governing light’s behavior.”

“You’re gonna have to explain that Lorentz thing.”

“Lorentz symmetry has to do with phenomena an observer sees near an object when their speed relative to the object approaches some threshold. Einstein’s Special Relativity theory predicted that gravity would also have Lorentz symmetry. Observations showed he was right.”

“So they both do Lorentz stuff. That makes them the same?”

“Oh, no, completely different physics but they share the same underlying structure. Maxwell’s equations say that light’s threshold is lightspeed.”

“Gravity does lightspeed, too, I suppose.”

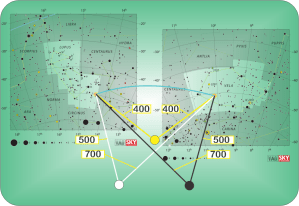
“There were arguments about that. Einstein said beauty demands that both use the same threshold. Other people said, ‘Prove it.’ The strongest argument in his favor at the time was rough, indirect, complicated, and had to do with fine details of Earth’s orbit around the Sun. Half a century later pulsar timing data gave us an improved measurement, still indirect and complicated. This one showed gravity’s threshold to be with 0.2% of lightspeed.”

“Anything direct like I could understand it?”

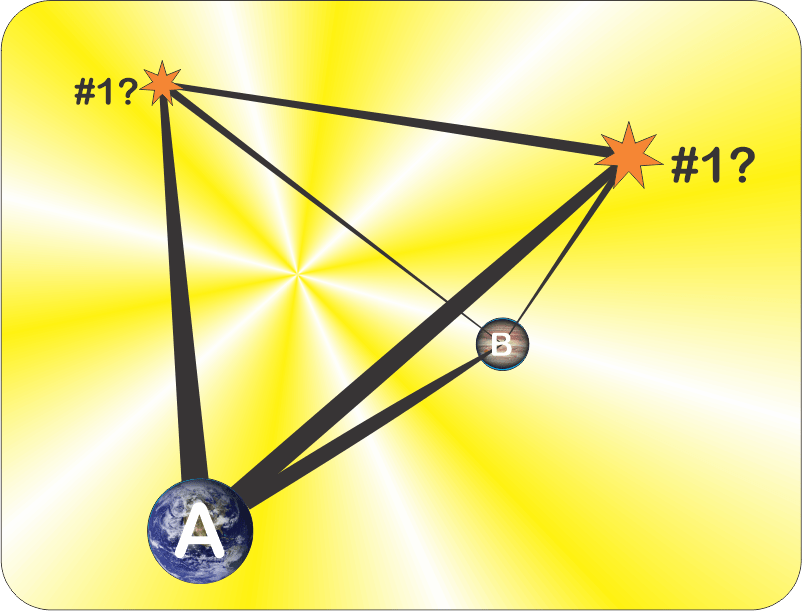
“How about a straight‑up horse race? In 2017, the LIGO facility picked up a gravitational signal that came in at the same time that optical and gamma ray observatories recorded pulses from the same source, a colliding pair of neutron stars in a galaxy 130 million lightyears away. A long track, right?”

“Waves, not horses, but how far apart were the signals?”

“Close enough that the measured speed of gravity is within 10–15 of the speed of light.”

“A photo-finish.”

“Nice pun, Mr Feder. We’re about 8½ light-minutes away from the Sun so we’re also 8½ gravity-minutes from the Sun. As the TV announcer said, if the Sun were to suddenly dematerialize then Earth would lose the Sun’s orbital attraction 8½ minutes later. We as individuals wouldn’t go floating off into space, though. Earth’s gravity would still hold us close as the whole darkened, cooling planet leaves orbit and heads outward.”

“I like it better staying close to home.”

~ Rich Olcott

A No-Charge Transaction

On By rolcottIn Cosmology, Crazy Theories, Physics: Light and Relativity, UncategorizedLeave a comment

“I ain’t done yet, Sy. I got another reason for Dark Matter being made of faster‑then‑light tachyons.”

“I’m still listening, Vinnie.”

“Dark Matter gotta be electrically neutral, right, otherwise it’d do stuff with light and that doesn’t happen. I say tachyons gotta be neutral.”

“Why so?”

“Stands to reason. Suppose tachyons started off as charged particles. The electric force pushes and pulls on charges hugely stronger than gravity pulls—”

“1036 times stronger at any given distance.”

“Yeah, so right off the bat charged tachyons either pair up real quick or they fly away from the slower‑than‑light bradyon neighborhood leaving only neutral tachyons behind for us bradyon slowpokes to look at.”

“But we’ve got un‑neutral bradyon matter all around us — electrons trapped in Earth’s Van Allen Belt and Jupiter’s radiation belts, for example, and positive and negative plasma ions in the solar wind. Couldn’t your neutral tachyons get ionized?”

“Probably not much. Remember, tachyon particles whiz past each other too fast to collect into a star and do fusion stuff so there’s nobody to generate tachyonic super‑high‑energy radiation that makes tachyon ions. No ionized winds either. If a neutral tachyon collides with even a high-energy bradyon, the tachyon carries so much kinetic energy that the bradyon takes the damage rather than ionize the tachyon. Dark Matter and neutral tachyons both don’t do electromagnetic stuff so Dark Matter’s made of tachyons.”

“Ingenious, but you missed something way back in your initial assumptions.”

“Which assumption? Show me.”

“You assumed that tachyon mass works the same way that bradyon mass does. The math says it doesn’t.” <grabbing scratch paper for scribbling> “Whoa, don’t panic, just two simple equations. The first relates an object’s total energy E to its rest mass m and its momentum p and lightspeed c.”

E² = (mc²)² + (pc)²

“I recognize the mc² part, that’s from Einstein’s Equation, but what’s the second piece and why square everything again?”

“The keyword is rest mass.”

“Geez, it’s frames again?”

“Mm‑hm. The (mc²)² term is about mass‑energy strictly within the object’s own inertial frame where its momentum is zero. Einstein’s famous E=mc² covers that special case. The (pc)² term is about the object’s kinetic energy relative to some other‑frame observer with relative momentum p. When kinetic energy is comparable to rest‑mass energy you’re in relativity territory and can’t just add the two together. The sum‑of‑squares form makes the arithmetic work when two observers compare notes. Can I go on?”

“I’m still waitin’ to hear about tachyons.”

“Almost there. If we start with that equation, expand momentum as mass times velocity and re‑arrange a little, you get this formula

E = mc² / √(1 – v²/c²)

The numerator is rest‑mass energy. The v²/c² measures relative kinetic energy. The Lorentz factor down in the denominator accounts for that. See, when velocity is zero the factor is 1.0 and you’ve got Einstein’s special case.”

“Give me a minute. … Okay. But when the velocity gets up to lightspeed the E number gets weird.”

“Which is why c is the upper threshold for bradyons. As the velocity relative to an observer approaches c, the Lorentz factor approaches zero, the fraction goes to infinity and so does the object’s energy that the observer measures.”

“Okay, here’s where the tachyons come in ’cause their v is bigger than c. … Wait, now the equation’s got the square root of a negative number. You can’t do that! What does that even mean?”

“It’s legal, when you’re careful, but interpretation gets tricky. A tachyon’s Lorentz factor contains √(–1) which makes it an imaginary number. However, we know that the calculated energy has to be a real number. That can only be true if the tachyon’s mass is also an imaginary number, because i/i=1.”

“What makes imaginary energy worse than imaginary mass?”

“Because energy’s always conserved. Real energy stays that way. Imaginary mass makes no sense in Newton’s physics but in quantum theory imaginary mass is simply unstable like a pencil balanced on its point. The least little jiggle and the tachyon shatters into real particles with real kinetic energy to burn. Tachyons disintegrating may have powered the Universe’s cosmic inflation right after the Big Bang — but they’re all gone now.”

“Another lovely theory shot down.”

~ Rich Olcott

Properties of Space

On By rolcottIn Cosmology, Physics: Electromagnetism, Physics: Waves, UncategorizedLeave a comment

Vinnie gives me the side‑eye. “Wait, Sy. Back there you said Maxwell got the speed of light from the properties of space. What does any of that even mean?”

“Do you remember Newton’s equation for the force of gravity between two objects?”

“Of course not. Lessee… the force’d be bigger when either one gets bigger, and it’d get smaller when the distance between ’em gets bigger and there’s some constant number to make the units right, right?”

“Close enough, it’s the distance squared. The equation’s F=Gm1m2/r². The G is the constant you mentioned. It does more than turn mass‑units times mass‑units divided by length‑units‑squared into force‑units. It says how many force‑units. For one pair of objects at a certain distance, turn the G‑dial up and you get more force. Make sense?”

“Yeah, that looks right.”

“The value of G sets the force‑distance scale for how two objects attract each other everywhere in the Universe. That value is a property of space. So is the fact that the value is the same in all directions.”

“Huh! Never thought of it like a scale factor. Space has other properties like that?”

“Certainly. Coulomb’s Law for the electrostatic force between two charged objects has the same basic structure, FE=–(q1q2/r²)/CE. In any units you like you replace the q‘s with object charge amounts and r with the distance between them. For each set of change‑ and distance‑units there’s a well‑researched value of CE to convert your charge and distance numbers into force‑units. Under the covers, though, CE is a scale factor that controls the range of the electrostatic force. It’s the same everywhere in the Universe and it’s completely independent of Newton’s gravity scale factor.”

“Hey, what about ‘like charges repel, opposites attract’?”

“That’s what the minus sign’s in there for. If the q‘s have the same charge, the force is negative, that’s repulsion; opposite charges make for positive, attractive force.”

“If there’s a CE for electric there’s gotta be a CM for magnetic.”

“Sort of. The electrostatic force doesn’t care about direction. Magnetism does care so the equation’s more complicated. You’re right, though, there is a similar universal scale factor we might as well call CM.”

<chuckle> “Electric, magnetic, I don’t suppose we could mix those two somehow for an electromagnetic scale factor?”

<grin> “Did you read ahead in the book? Yes we can, and Maxwell’s equations showed us how. If you multiply the two C‘s together, you get one over the square of the speed of light. Re‑arranging a little, c=√(1/CECM), so c, the electromagnetic scale factor for velocity, is based on those space properties. Einstein showed that no material object can have a velocity greater than c.”

“I’ll take your word for the arithmetic, but how does that combination make for a speed limit?”

“There’s an easy answer you’re not going to like — it’s a speed because the units come out meters per second.”

“That’s a cheat. I don’t like it at all and it doesn’t account for the limit part. Explain it with Physics, no fancy equations.”

“Tough assignment. Okay, typical waves have a displacement force, like wind or something pushing up on an ocean wave, that works against a restoring force, such as gravity pulling down. Electromagnetic waves are different. The electric component supplies the up force, but the magnetic component twists sideways instead of restoring down. The wave travels as a helix. The CE and CM properties determine how tightly it spirals through space. That’s lightspeed.”

“And the limit part?”

“Einstein maintained that anything that happens must follow the same rules for all observers no matter how each is moving. The only way that can be true is if space is subject to the Lorentz contraction √[1-(v/vmax)²] for some universal maximum speed vmax. Maxwell’s electromagnetism equations showed that vmax is c. Okay?”

“I suppose.”

~ Rich Olcott

  • * Vinnie hates equations even with regular letters, Greek letters make it worse. Hence my using CE and CM instead of the conventional ε0 and μ0 notation. Sue me.

The Time Is Out of Joint

On By rolcottIn Cosmology, Crazy Theories, UncategorizedLeave a comment

Vinnie galumphs over to our table. “Hi, guys. Hey, Sy, I just read your Confluence post. I thought that we gave up on things happening simultaneous because of Einstein and relativity but I guess that wasn’t the reason.”

“Oh, things do happen simultaneously, no‑one claims they don’t, it’s just that it’s impossible for two widely‑separated observers to have evidence that two widely‑separated events happened simultaneously. That’s a very different proposition.”

“Ah, that makes me feel better. The ‘nothing is simultaneous‘ idea was making me itchy ’cause I know for sure that a good juggler lets go with one hand just as they’re catching with the other. How’s Einstein involved then?”

“Lightspeed’s a known constant. Knowing distance and lightspeed lets you calculate between‑event time, right? The key to simultaneity was understanding why lightspeed is a constant. We’d known lightspeed wasn’t infinite within the Solar System since Rømer’s time, but people doubted his number applied everywhere. Maxwell’s theory of electromagnetism derived lightspeed from the properties of space itself so it’s universal. Only in Newton’s Universe was it possible for two distant observers to agree that two also‑distant events were simultaneous.”

“Why was Newton’s Universe special?

“Space held still and didn’t bend. Astronomers A and B had a stable baseline between them. After measuring the baseline with light they could measure the angles each observed between the events. Some trigonometry let them send each other congratulatory messages on seeing a simultaneous pair of incidents. After Einstein’s work, they knew better.”

“It’s frames again, ain’t it?”

“Of course, Vinnie. A‘s frame is almost certainly moving relative to B‘s frame. Motion puts the Lorentz relativity factor into the game, making each astronomer’s clock run faster than the other’s. Worse, each astronomer sees that the other’s yardsticks are too short.”

Jeremy gives me a confused look.

“Space compression goes along with time dilation, Jeremy. Professor Hanneken will explain it all when your class gets to that unit. Bottom line, things can happen simultaneously in Einstein’s Universe, but no‑one can agree on which things.”

“Wait, if every frame has its own time‑rate, how can two spaceships rendezvous for an operation?”

“Good question, Jeremy. Einstein had an answer but complications hide under the covers. He suggested that A start a timer when sending a light pulse to a mirror at B. A waits for the reflection. B starts a timer when they see A‘s pulse. A measures the pulse’s round‑trip time. Each creates a clock that advances one tick for half of the round-trip time. B sets their clock back by one tick. That done, they agree to meet some number of ticks later.”

“Hmm… That should work, but you said there are complications.”

“There are always complications. For instance, suppose B is slingshotting around a black hole so that pulse and reflection travel different pathlengths. Or suppose one frame is rotating edge‑on to the other. In practice the ships would re‑sync repeatedly while approaching the rendezvous point.”

Vinnie erupts. “HAW! Successive approximation again!”

“Indeed. If we could extend the method to more than two participants we’d have a true Universal Coordinated Time.”

“Don’t we have that, Mr Moire? The Big Bang happened 14 billion years ago. Couldn’t we measure time from that?”

“Sort of. Last I looked the number was 13.787 plus‑or‑minus 20 million years. Too much slop for an instantaneous fleet‑level rendezvous like the final battle scene in StarTrek:Picard. But you’ve brought up an interesting question for a Crazy Theories seminar. One of Cosmology’s deepest unsolved questions is, ‘How does inertia work?’ Do you remember Newton’s First Law?”

<closes eyes> “In an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.“

“Right. In other words, every object resists change to its current steady motion along a geodesic. Why is that? There’s no coherent, well‑founded, well‑tested theory. Einstein liked Mach’s Principle, which says inertia exists because every object is attracted through space to all the mass in the Universe. Suppose there’s a Mach’s Principle for Time, saying that objects squirt up the Time axis because they’re repelled by all the mass in the Universe.”

Vinnie hoots, “Bo-o-o-ohh-GUS!”

~ Rich Olcott

Hillerman, Pratchett And Narrativium

On By rolcottIn Astronomy, General: Fun Stuff, UncategorizedLeave a comment

No-one else in the place so Jeremy’s been eavesdropping on my conversation with Cal. “Lieutenant Leaphorn says there are no coincidences.”

“Oh, you’ve read Tony Hillerman’s mystery stories then?”

“Of course, Mr Moire. It’s fun getting a sympathetic outsider’s view of what my family and Elders have taught me. He writes Leaphorn as a very wise man.”

“With some interesting quirks for a professional crime solver. He doesn’t trust clues, yet he does trust apparent coincidences enough to follow up on them.”

“It does the job for him, though.”

“Mm‑hm, but that’s in stories. Have you read any of Terry Pratchett’s Discworld books?”

“What are they about?”

From Terry Pratchett’s book
Carpe Jugulum

“Pretty much everything, but through a lens of laughter and anger. Rather like Jonathan Swift. Pratchett was one of England’s most popular authors, wrote more than 40 novels in his too‑brief life. He identified narrativium as the most powerful force in the human universe. Just as the nuclear strong force holds the atomic nucleus together using gluons and mesons, narrativium holds stories together using coincidences and tropes.”

“Doesn’t sound powerful.”

“Good stories, ones that we’d say have legs, absolutely must have internal logic that gets us from one element to the next. Without that narrative flow they just fall apart; no‑one cares enough to remember them. As a writer myself, I’ve often wrestled with a story structure that refused to click together — sparse narrativium — or went in the wrong direction — wayward narrativium.”

“You said ‘the human universe’ like that’s different from the Universe around us.”

“The story universe is a multiverse made of words, pictures and numbers, crafted by humans to explain why one event follows another. The events could be in the objective world made of atoms or within the story world itself. Legal systems, history, science, they’re all pure narrativium. So is money, mostly. We don’t know of anything else in the Universe that builds stories like we do.”

“How about apes?”

“An open question, especially for orangutans. One of Pratchett’s important characters is The Librarian, a university staff member who had accidentally been changed from human to orangutan. He refuses to be restored because he prefers his new form. Which gives you a taste of Pratchett’s humor and his high regard for orangutans. But let’s get back to Leaphorn and coincidences.”

“Regaining control over your narrativium, huh?”

“Guilty as charged. Leaphorn’s standpoint is that there are no coincidences because the world runs on patterns, that events necessarily connect one to the next. When he finds the pattern, he solves the mystery.”

“Very Diné. Our Way is to look for and restore harmony and balance.”

“Mm‑hm. But remember, Leaphorn is only a character in Hillerman’s narrativium‑driven stories. The atom‑world may not fit that model. A coincidence for you may not be a coincidence for someone else, depending. Those two concurrent June novas, for example. For most of the Universe they’re not concurrent.”

“I hope this doesn’t involve relativistic clocks. Professor Hanneken hasn’t gotten us to Einstein’s theories yet.”

Adapted from images by
IAU and Sky & Telescope magazine
(Roger Sinnott & Rick Fienberg)
CC BY 3.0

“No relativity; this is straight geometry. Rømer could have handled it 350 years ago.” <brief tapping on Old Reliable’s screen> “Here’s a quick sketch and the numbers are random. The two novas are connected by the blue arc as we’d see them in the sky if we were in Earth’s southern hemisphere. We live in the yellow solar system, 400 lightyears from each of them so we see both events simultaneously, 400 years after they happened. We call that a coincidence and Cal’s skywatcher buddies go nuts. Suppose there are astronomers on the white and black systems.”

<grins> “Those four colors aren’t random, Mr Moire.”

<grins back> “Caught me, Jeremy. Anyway, the white system’s astronomers see Vela’s nova 200 years after they see the one in Lupus. The astronomers in the black system record just the reverse sequence. Neither community even thinks of the two as a pair. No coincidence for them, no role for narrativium.”

~ Rich Olcott

  • This is the 531st post in an unbroken decade‑long weekly series that I originally thought might keep going for 6 months. <whew!>

Sussing Out The Unseeable

On By rolcottIn Astronomy: Techniques, Cosmology, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“Hello, Mr Moire.”

“Afternoon, Walt. Pizza time again?”

“No, too public. Poor craft to be seen too often in the same place. There’s a park bench by the lake.”

“I know the spot.”

“Fifteen minutes.”

“Twenty.”

“Afternoon, Walt. What are your people curious about this time?”

“Word is that astronomers uncovered a huge amount of matter they’d been searching for. We’re interested in concealment techniques, so we want to know how it was hidden and how was it found.”

“Forty percent of all baryonic matter—”

“Baryonic?”

“Made out of atoms. Baryons are multi-quark particles like protons and—”

“Leave the weeds and get back to the topic. Where was that 40% hiding?”

“In plain sight, all over the sky, in strands forming a network that connects galaxies and galaxy clusters. They’re calling it the Cosmic Web.”

“Something that big … how was hidden?”

“Some techniques I’m sure you’ll recognize. First, the material in the strands is diffuse — just an atom or two per cubic meter. An Earth laboratory would be proud to pump down a vacuum ten million times more dense.”

<taking notes> “Spread your forces so there’s no prime target for counter‑attack, mm‑hm. But if the material’s that thin, surely it doesn’t mass much.”

“Remember how big space is. These filaments span the widths of multiple galaxies. Do the math. A thread could be on the order of 100 million lightyears long by 1000 lightyears in diameter. A lightyear is 1016 meters. The thread has a volume of about 1062 cubic meters. At 10-26 kilogram per cubic meter that’s 1036 kilograms which is comparable to the mass of a small galaxy. That’s just one thread. Add them up and you get roughly half the baryons in the Universe, all hiding in the Web.”

“Concealment by dispersal, got it. What’s another technique?”

“Camouflage. No, not tiny uniforms in a woodland pattern. These atoms fade into the background because oncoming light waves pass right by them unless the wave has exactly the right wavelength for an absorption.”

“So how did astronomers detect these scattered and camouflaged atoms?”

“A couple of different ways. X‑rays, for one.”

“But these atoms are camouflaged against passing light. X‑rays are light waves.”

“X‑rays the atoms emit. Everybody thinks that space is cold, but those lonely atoms bounce around with a kinetic energy equivalent to million‑degree temperatures. When two of them collide some of that kinetic energy escapes as high‑frequency light, X‑ray range. Not a whole lot, because the atoms are sparse, but enough that European and Japanese space telescopes were able to tweeze it out of the background.”

“Use sensitive mics to pick up whispered convo in the opposing line.”

<pause> “Right, more or less. What do you know about refraction?”

“Mmm… Newton and his prism, splitting white light into different colors. I’ve no idea how that works.”

“The short answer is that the speed of light depends on its wavelength and the medium it’s traversing. In a perfect vacuum, light always goes at top speed just like Einstein said, but charged particles in its path slow it down.”

“Even those atoms in space that you said can’t absorb light?”

“Yup. It’s called virtual coupling; quantum’s involved. One inaccurate way to describe the interaction is that atoms occasionally absorb wrong‑wavelength photons but spit them right back out again after a brief delay. Short wavelengths see more of that effect than long wavelengths do. With me?”

<pause> “Go on.”

“Does the phrase ‘Fast Radio Burst’ sound familiar?”

“Of course, but probably not the way you mean.”

“Ah. Right. For this context, Fast Radio Bursts are isolated pulses of radio‑frequency light from incredibly bright extra-galactic sources we don’t understand. They’re all over the sky. A pulse lasts only a millisecond or so. What’s important here is that refraction skews each pulse’s wavelength profile as it travels through the intergalactic medium. Researchers analyze the distortions to detect and characterize Web filaments in the direction each pulse came from.”

“Intercept the oppo’s communications to the front.”

“That’s about the size of it.”

“Bye.”

“Don’t mention it.”

The Cosmic Web
Visualization: Frank Summers (STScI); Simulation: Martin White and Lars Hernquist, Harvard University

~ Rich Olcott

Black, White And Wormy

On By rolcottIn Cosmology, Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

“Whaddaya mean, Sy, if white holes exist? You just told me how they’re in the equations just like black holes.”

“Math gives us only models of reality, Vinnie. Remarkably good models, some of them, but they’re only abstractions. Necessarily they leave out things that might skew math results away from physical results or the other way around. Einstein believed his math properly reflected how the Universe works, but even so, he doubted that black holes could exist. He didn’t think it’d be possible to collect that much mass into such a small space. Two decades after he said that, Oppenheimer figured out how that could happen.”

“Oppenheimer like the A‑bomb movie guy?”

“Same Oppenheimer. He was a major physicist even before they put him in charge of the Manhattan Project. He did a paper in 1939 showing how a star‑collapse could create the most common type of black hole we know of. Twenty‑five years after that the astronomers found proof that black holes exist.”

“Well, if Einstein was wrong about black holes, why wasn’t he wrong about white holes?”

“We need another Oppenheimer to solve that. So far, no‑one has come up with a mechanism that would create a stand‑alone white hole. That level of stress on spacetime requires an enormous amount of mass‑energy in a tiny volume. Whatever does that must somehow do it with a time‑twist opposite to how a black hole is formed. Worse yet, by definition the white hole’s Event Horizon leaks matter and energy. The thing ought to evaporate almost as soon as it’s formed.”

“I heard weaseling. You said, ‘a stand‑alone white hole,’ like there’s maybe another kind. How about that?”

“Could be, maybe not, depending on who’s talking and whether or not they’re accounting for magnetic fields, neutrinos or quantum effects. The discussion generally involves wormholes.”

“Wormholes.”

“Mm-hm. Some cosmologists think that wormholes might bridge between highly stressed points in spacetime. Black hole or white, the stress is what matters. The idea’s been around nearly as long as our modern idea of black holes. No surprise, ‘wormhole’ was coined by John Archibald Wheeler, the same guy who came up with the phrases ‘black hole’ and ‘quantum foam’.”

“Quantum—. Nope, not gonna bite. Get back to white holes.”

“I’m getting there. Anyway, the relativity theory community embraced black holes, white holes and wormholes as primary tools for studying how spacetime works.”

“How’re they gonna do that? That squib Cal showed me said we’ve never seen a white hole.”

“Fair question. Last I heard, the string theory community confidently predicted 10500 different Universes with little hope of narrowing the field. In contrast, relativity theory is firmly constrained by well‑founded math, a century of confirmation from experimental tests and a growing amount of good black hole data. Perfectly good math says that wormholes and white holes could form but only under certain unlikely conditions. Those conditions constrain white holes like Oppenheimer’s conditions constrained forming a stellar‑size black hole.”

“So how do we make one?”

“We don’t. If the Universe can make the right conditions happen somewhere in spacetime, it could contain white holes and maybe a network of wormholes; otherwise, not. Maybe we don’t see them because they’ve all evaporated.”

“I remember reading one time that with quantum, anything not forbidden must happen.”

“Pretty much true, but we’re not talking quantum here. Macro‑scale, some things don’t happen even though they’re not forbidden.”

“Name one.”

“Anti‑matter. The laws of physics work equally well for atoms with positive or negative nuclear charge. We’ve yet to come up with an explanation for why all the nuclear matter we see in the Universe has the positive‑nucleus structure. The mystery’s got me considering a guess for Cathleen’s next Crazy Theories seminar.”

“Oh, yeah? Let’s have it.”

“Strictly confidential, okay?”

“Sure, sure.”

“Suppose the Big Bang’s chaos set up just the right conditions to make a pair of CPT‑twin black holes, expanding in opposite directions along spacetime’s time dimension. Suppose we’re inside one twin. Our time flows normally. If we could see into the other twin, we’d see inside‑out atoms and clocks running backwards. From our perspective the twin would be a white hole.”

“Stay outta that wormhole bridge.”

~ Rich Olcott

A High-contrast Image

On By rolcottIn Cosmology, Physics: Black Holes and Relativity, UncategorizedLeave a comment

Vinnie clomps into my office. “Morning, Sy. I knew you weren’t busy ’cause there’s music playing.”

“Well, you’re right, I am between assignments. Yesterday another client called to say they’re cancelling my contract because their Federal grant was cut off. They had to let three grad students go, too. That was a project with good prospects for generating a couple of successful businesses. These zealots are eating our seed corn, Vinnie, and they’re burning down the silo.”

“I know the feeling, Sy. There’s a lot less charter flying to do these days. Nobody wants to do meetings when they don’t know what the rules will be next week.”

<deep sigh>
 <deep sigh>

“Oh, yeah, Sy. Why I came up here — what’s with white holes? Cal asked me about ’em ’cause a little squib in one of his astronomy magazines didn’t tell us much so now I’m curious.”

“Okay, tell me something you know about black holes.”

“We can’t see one, but we can see light from its accretion disc.”

“Fair enough. Something else.”

“A black hole’s what you get when a right‑size star collapses.”

“I like that ‘right‑size’ qualification. Too small or too big doesn’t work. White holes almost certainly can’t happen from a star collapse. What else?”

“I heard that ‘almost.’ Uhh… once you pass inside the Event Horizon, you can’t get out.”

“You can’t get inside a white hole’s Event Horizon.”

“Okay, that’s weird. Like it’s got a hard crust like black holes don’t?”

“Nope. A white hole’s Event Horizon’s a mathematical abstraction just like a black hole’s. Not a hard surface, just a boundary where time starts playing games.”

“Wait, we talked about time and the Event Horizon some time ago. If I remember right, we worked out that cause‑and‑effect runs parallel to time. Outside the Event horizon time’s not locked to any specific orientation in space. We can cause things to happen in any direction. Inside the Event Horizon’s sphere, both time and cause‑and‑effect point further in. You can’t make anything happen further out than wherever you are in there which is why light can’t escape, right?”

“Mostly. Anything inside the Horizon is bound to spiral inward toward the singularity. The journey could be slow or fast. There’s some disagreement on how long it would take, though — could be forever, could be forever near enough. Some current models say the Horizon’s geometric center is the infinitely distant future. Other models say, no, for a stellar‑collapse black hole it’s only beyond the age of the Universe.”

“Why not … oh, because the real black hole was born at a definite time so it can’t have an infinite future.”

“That’s about the size of it — both directions either finite or infinite. Physicists love to propose symmetries like that but I’m not willing to bet either way.”

“Black hole/white hole sounds like symmetry.”

“In a way it isn’t, in a way it is. Both varieties are solutions for Einstein’s equation about spacetime under—”

“Hold it, no equations, you know I hate those things. Anyway, how can two different holes solve one equation?”

“Solve x=√9.”

“Gotta be x=3.”

“Or minus‑3. They’re both right answers, right?”

“Mmm, yeah. Okay, that was arithmetic, not an equation, but why’d you give it to me at all?”

“To demonstrate plus‑or‑minus symmetry. Einstein’s equation tells how mass warps spacetime. The answers relate to square‑roots of summed squares like Pythagoras’ c=√(a²+b²). If you pick positive square roots the warping describes a black hole. The negative square roots give the warping for a white hole which behaves differently. Both kinds depend on intense gravitational fields arising from a singularity but a white hole’s cause‑and‑effect arrow points outward.”

“So that’s why you’re locked out? You can’t cause anything further in than you are?”

“Exactly. But it gets deeper. A black hole’s singularity, the one you can’t avoid if you’re inside its Event Horizon, is in the distant future. A white hole’s singularity, the one you can’t get to anyway, is in the distant past.”

“That’s why you said they can’t come from star collapses — the stars died too recent.”

“Mm-hm. If white holes exist at all, they probably were born in the Big Bang.”

~ Rich Olcott

A Play Beyond The Play

On By rolcottIn Cosmology, Gravitational astronomy, Uncategorized, Vera RubinLeave a comment

Vinnie takes a long thoughtful look at the image that had dashed his beautiful six‑universe idea. “Wait, Sy. I don’t like this picture”

“Because it messes up your invention?”

“No, because how can they know what that halo looks like? I mean, the whole thing with dark matter is that we can’t see it.”

“You’re right about that. Dark matter’s so transparent that even with five times more mass than normal matter, it doesn’t block CMB photons coming from 13.8 billion lightyears away. That still boggles my brain every once in a while. But dark matter’s gravitational effects — those we can see.”

“Yeah, I remember a long time ago we talked about Fritz Zwicky and Vera Rubin and how they told people about galaxies held together by too much gravity but nobody believed them.”

“Well, they did, after a while—”

“A long while, like a long while since those talks. Remind me what ‘too much gravity’ was about.”

“It was about conflicts between their observations and the prevailing theoretical models. Everyone thought that galaxies and galaxy clusters should operate pretty much like planetary orbits — your speed increases the closer you are to the center, up to Einstein’s speed limit. Newton’s Laws of Motion predict how fast you should move if you’re at a certain distance from a body with a certain mass. If you’re moving faster than that, you fly away.”

“Yeah, escape velocity. So the galaxies in Zwicky’s cluster didn’t follow Newton’s Laws?”

“They didn’t seem to. Galaxies that should have escaped were still in there. The only way he could explain the stability was to suppose the galaxies are only a small fraction of the cluster’s mass. Extra gravity from the extra mass must bind things together. Forty years later Rubin’s improved technology revealed that stars within galaxies had the same anomalous motion.”

“I’m guessing the ‘faster near the center’ rule didn’t hold, or else you wouldn’t be telling this story. Spun like a wheel, I bet.”

“When a wheel spins, every part of it rotates at the same angular speed, the same number of degrees per second, right?”

“Ahh, the bigger my circle the higher my airspeed so the rule would be ‘faster farther out’.”

“That’s the wheel rule, right, but Rubin’s data showed that stars within galaxies don’t obey that one either. She measured lots of stars in Andromeda and other galaxies. Their linear speeds, kilometers per second, are nearly identical from near the center all the way out. Even dust and gas clouds beyond the galactic starry edges also fit the ‘same linear speed everywhere’ rule. You’d lose the bet.”

“That just doesn’t feel right. How can just gravity make that happen?”

“It can if the right amount of dark matter’s distributed in the right‑shaped smeared‑out hollowed‑out spherical halo. The halo’s radial density profile looks about like this. Of course, profiles for different galaxies differ in spread‑outness and other details, but the models are pretty consistent.”

“Wait, if dark matter only does gravity like you said, why’s that hole in the middle? Why doesn’t everything just fall inward?”

“Dark matter has mass so it also has inertia, momentum and angular momentum, just as normal matter does. Suppose some of the dark matter has collected gravitationally into a blob and the blob is moving slower than escape velocity. If it’s flying straight at the center of gravity it’ll get there and stay there, more or less. But if the blob’s aimed in any other direction, it has angular momentum relative to the center. Momentum’s conserved for dark matter, too. The blob eventually goes into orbit and winds up as part of the shell.”

“Does Zwicky’s galaxy cluster have a halo, too?”

“Not in the same way. Each galaxy probably has its own halo but the galaxies are far apart relative to their size. The theoreticians have burned huge amounts of computer time simulating the chaos inside large ensembles of gravity‑driven blobs. I just read one paper about a 4‑billion‑particle calculation and mind you, a ‘particle’ in this study carried more than a million solar masses. Big halos host subhalos, with filaments of minihalos tying them together. What we can’t see is complicated, too.”

~ Rich Olcott

Hiding Under Many Guises

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized3 Comments

Vinnie lifts his pizza slice and pauses. “I dunno, Sy, this Pressure‑Volume part of enthalpy, how is it energy so you can just add or subtract it from the thermal and chemical kinds?”

“Fair question, Vinnie. It stumped scientists through the end of Napoleon’s day until Sadi Carnot bridged the gap by inventing thermodynamics.”

“Sounds like a big deal from the way you said that.”

“Oh, it was. But first let’s clear the ‘is it energy?’ question. How would Newton have calculated the work you did lifting that slice?”

“How much force I used times the distance it moved.”

“Putting units to that, it’d be force in newtons times distance in meters. A newton is one kilogram accelerated by one meter per second each second so your force‑distance work there is measured in kilograms times meters‑squared divided by seconds‑squared. With me?”

“Hold on — ‘per second each second’ turned into ‘per second‑squared.” <pause> “Okay, go on.”

“What’s Einstein’s famous equation?”

“Easy, E=mc².”

“Mm-hm. Putting units to that, c is in meters per second, so energy is kilograms times meters‑squared divided by seconds‑squared. Sound familiar?”

“Any time I’ve got that combination I’ve got energy?”

“Mostly. Here’s another example — a piston under pressure. Pressure is force per unit area. The piston’s area is in square meters so the force it feels is newtons per meter‑squared, times square meters, or just newtons. The piston travels some distance so you’ve got newtons times meters.”

“That’s force‑distance work units so it’s energy, too.”

“Right. Now break it down another way. When the piston travels that distance, the piston’s area sweeps through a volume measured in meters‑cubed, right?”

“You’re gonna say pressure times volume gives me the same units as energy?”

“Work it out. Here’s a paper napkin.”

“Dang, I hate equations … Hey, sure enough, it boils down to kilograms times meters‑squared divided by seconds‑squared again!”

“There you go. One more. The Ideal Gas Law is real simple equation —”

“Gaah, equations!”

“Bear with me, it’s just PV=nRT.”

“Is that the same PV so it’s energy again?”

“Sure is. The n measures the amount of some gas, could be in grams or whatever. The R, called the Gas Constant, is there to make the units come out right. T‘s the absolute temperature. Point is, this equation gives us the basis for enthalpy’s chemical+PV+thermal arithmetic.”

“And that’s where this Carnot guy comes in.”

“Carnot and a host of other physicists. Boyle, Gay‑Lussac, Avagadro and others contributed to Clapeyron’s gas law. Carnot’s 1824 book tied the gas narrative to the energetics narrative that Descartes, Leibniz, Newton and such had been working on. Carnot did it with an Einstein‑style thought experiment — an imaginary perfect engine.”

“Anything perfect is imaginary, I know that much. How’s it supposed to work?”

<sketching on another paper napkin> “Here’s the general idea. There’s a sealed cylinder in the middle containing a piston that can move vertically. Above the piston there’s what Carnot called ‘a working body,’ which could be anything that expands and contracts with temperature.”

“Steam, huh?”

“Could be, or alcohol vapor or a big lump of iron, whatever. Carnot’s argument was so general that the composition doesn’t matter. Below the piston there’s a mechanism to transfer power from or to the piston. Then we’ve got a heat source and a heat sink, each of which can be connected to the cylinder or not.”

“Looks straight‑forward.”

“These days, sure. Not in 1824. Carnot’s gadget operates in four phases. In generator mode the working body starts in a contracted state connected to the hot Th source. The body expands, yielding PV energy. In phase 2, the body continues to expand while it while it stays at Th. Phase 3, switch to the cold Tc heat sink. That cools the body so it contracts and absorbs PV energy. Phase 4 compresses the body to heat it back to Th, completing the cycle.”

“How did he keep the phases separate?”

“Only conceptually. In real life Phases 1 and 2 would occur simultaneously. Carnot’s crucial contribution was to treat them separately and yet demonstrate how they’re related. Unfortunately, he died of scarlet fever before Clapeyron and Clausius publicized and completed his work.”

~ Rich Olcott