Tag: Einstein

Would the CIA want a LIGO?

On By rolcottIn Astronomy: Techniques, Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Electromagnetism, Physics: Fundamentals, Physics: Light and Relativity, UncategorizedLeave a comment

So I was telling a friend about the LIGO announcement, going on about how this new “device” will lead to a whole new kind of astronomy.  He suddenly got a far-away look in his eyes and said, “I wonder how many of these the CIA has.”

The CIA has a forest of antennas, but none of them can do what LIGO does.  That’s because of the physics of how it works, and what it can and cannot detect.  (If you’re new to this topic, please read last week’s post so you’ll be up to speed on what follows.  Oh, and then come back here.)

There are remarkable parallels between electromagnetism and gravity.  The ancients knew about electrostatics — amber rubbed by a piece of cat fur will attract shreds of dry grass.  They certainly knew about gravity, too.  But it wasn’t until 100 years after Newton wrote his Principia that Priestly and then Coulomb found that the electrostatic force law, F = ke·q1·q2 / r2, has the same form as Newton’s Law of Gravity, F = G·m1·m2 / r2. (F is the force between two bodies whose centers are distance r apart, the q‘s are their charges and the m‘s are their masses.)

Jim and AlAlmost a century later, James Clerk Maxwell (the bearded fellow at left) wrote down his electromagnetism equations that explain how light works.  Half a century later, Einstein did the same for gravity.

But interesting as the parallels may be, there are some fundamental differences between the two forces — fundamental enough that not even Einstein was able to tie the two together.

One difference is in their magnitudes.  Consider, for instance, two protons.  Running the numbers, I found that the gravitational force pulling them together is a factor of 1036 smaller than the electrostatic force pushing them apart.  If a physicist wanted to add up all the forces affecting a particular proton, he’d have to get everything else (nuclear strong force, nuclear weak force, electromagnetic, etc.) nailed down to better than one part in 1036 before he could even detect gravity.

But it’s worse — electromagnetism and gravity don’t even have the same shape.

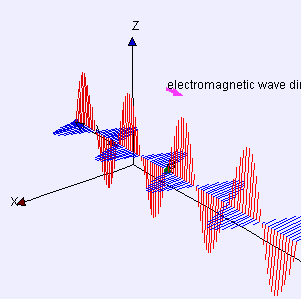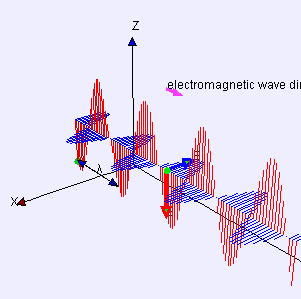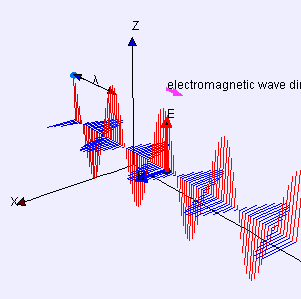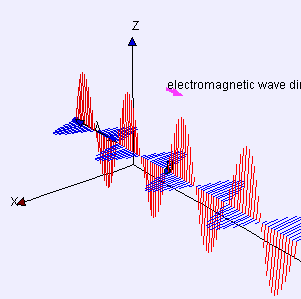
Electromagneticwave3D
Electric (red) and magnetic (blue) fields in a linearly polarized light wave
(graphic from WikiMedia Commons, posted by Lookang and Fu-Kwun Hwang)

A word first about words.  Electrostatics is about pure straight-line-between-centers (longitudinal) attraction and repulsion — that’s Coulomb’s Law.  Electrodynamics is about the cross-wise (transverse) forces exerted by one moving charged particle on the motion of another one.  Those forces are summarized by combining Maxwell’s Equations with the Lorenz Force Law.  A moving charge gives rise to two distinct forces, electric and magnetic, that operate at right angles to each other.  The combined effect is called electromagnetism.

The effect of the electric force is to vibrate a charge along one direction transverse to the wave.  The magnetic force only affects moving charges; it acts to twist their transverse motion to be perpendicular to the wave.  An EM antenna system works by sensing charge flow as electrons move back and forth under the influence of the electric field.

Gravitostatics uses Newton’s Law to calculate longitudinal gravitational interaction between masses.  That works despite gravity’s relative weakness because all the astronomical bodies we know of appear to be electrically neutral — no electrostatic forces get in the way.  A gravimeter senses the strength of the local gravitostatic field.

Maxwell and EinsteinGravitodynamics is completely unlike electrodynamics.  Gravity’s transverse “force” doesn’t act to move a whole mass up and down like Maxwell’s picture at left.  Instead, as shown by Einstein’s picture, gravitational waves stretch and compress while leaving the center of mass in place. I put “force” in quotes because what’s being stretched and compressed is space itself.  See this video for a helpful visualization of a gravitational wave.

LIGO is neither a telescope nor an electromagnetic antenna.  It operates by detecting sudden drastic changes in the disposition of matter within a “small” region.  In LIGO’s Sept 14 observation, 1031 kilograms of black hole suddenly ceased to exist, converted to gravitational waves that spread throughout the Universe.  By comparison, the Hiroshima explosion released the energy of 10-6 kilograms.

Seismometers do a fine job of detecting nuclear explosions.  Hey, CIA, they’re a lot cheaper than LIGO.

~~ Rich Olcott

LIGO, a new kind of astronomy

On By rolcottIn Astronomy: Techniques, Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Fundamentals, UncategorizedLeave a comment

Like thousands of physics geeks around the world, I was glued to the tube Thursday morning for the big LIGO (Laser Interferometer Gravitational-Wave Observatory) announcement.  As I watched the for-the-public videos (this is a good one), I was puzzled by one aspect of the LIGO setup.  The de-puzzling explanation spotlit just how different gravitational astronomy will be from what we’re used to.

There are two LIGO installations, 2500 miles apart, one near New Orleans and the other near Seattle.  Each one looks like a big L with steel-pipe arms 4 kilometers long.  By the way, both arms are evacuated to eliminate some sources of interference and a modest theoretical consideration.

LIGO3The experiment consists of shooting laser beams out along both arms, then comparing the returned beams.

Some background: Einstein conquered an apparent relativity paradox.  If Ethel on vehicle A is speeding (like, just shy of light-speed speeding) past Fred on vehicle B, Fred sees that Ethel’s yardstick appears to be shorter than his own yardstick.  Meanwhile, Ethel is quite sure that Fred’s yardstick is the shorter one.

Einstein explained that both observations are valid.  Fred and Ethel can agree with each other but only after each takes proper account of their relative motion.  “Proper account” is a calculation called the Lorenz transformation.   What Fred (for instance) should do is divide what he thinks is the length of Ethel’s yardstick by √[1-(v/c)²] to get her “proper” length.  (Her relative velocity is v, and c is the speed of light.)

Suppose Fred’s standing in the lab and Ethel’s riding a laser beam.  Here’s the puzzle: wouldn’t the same Fred/Ethel logic apply to LIGO?  Wouldn’t the same yardstick distortion affect both the interferometer apparatus and the laser beams?

Well, no, for two reasons.  First, the Lorenz effect doesn’t even apply, because the back-and-forth reflected laser beams are standing waves.  That means nothing is actually traveling.  Put another way, if Ethel rode that light wave she’d be standing as still as Fred.

The other reason is that the experiment is less about distance traveled and more about time of flight.

Suppose you’re one of a pair of photons (no, entanglement doesn’t enter into the game) that simultaneously traverse the interferometer’s beam-splitter mirror.  Your buddy goes down one arm, strikes the far-end mirror and comes back to the detector.  You take the same trip, but use the other arm.

The beam lengths are carefully adjusted so that under normal circumstances, when the two of you reach the detector you’re out of step.   You peak when your buddy troughs and vice-versa.  The waves cancel and the detector sees no light.

Now a gravitational wave passes by (red arcs in the diagram).  In general, the wave will affect the two arms differently.  In the optimal case, the wave front hits one arm broadside but cuts across the perpendicular one.  Suppose the wave is in a space-compression phase when it hits.  The broadside arm, beam AND apparatus, is shortened relative to the other one which barely sees the wave at all.

The local speed of light (miles per second) in a vacuum is constant.  Where space is compressed, the miles per second don’t change but the miles get smaller.  The light wave slows down relative to the uncompressed laboratory reference frame.  As a result, your buddy in the compressed arm takes just a leetle longer than you do to complete his trip to the detector.  Now the two of you are in-step.  The detector sees light, there is great rejoicing and Kip Thorne gets his Nobel Prize.

But the other wonderful thing is, LIGO and neutrino astronomy are humanity’s first fundamentally new ways to investigate our off-planet Universe.  Ever since Galileo trained his crude telescope on Jupiter the astronomers have been using electromagnetic radiation for that purpose – first visible light, then infra-red and radio waves.  In 1964 we added microwave astronomy to the list.  Later on we put up satellites that gave us the UV and gamma-ray skies.

The astronomers have been incredibly ingenious in wringing information out of every photon, but when you look back it’s all photons.  Gravitational astronomy offers a whole new path to new phenomena.  Who knows what we’ll see.

~~ Rich Olcott

Circular Logic

On By rolcottIn General: Fun Stuff, Mathematics, Uncategorized2 Comments

We often read “singularity” and “black hole” in the same pop-science article.  But singularities are a lot more common and closer to us than you might think. That shiny ball hanging on the Christmas tree over there, for instance.  I wondered what it might look like from the inside.  I got a surprise when I built a mathematical model of it.

To get something I could model, I chose a simple case.  (Physicists love to do that.  Einstein said, “You should make things as simple as possible, but no simpler.”)

I imagined that somehow I was inside the ball and that I had suspended a tiny LED somewhere along the axis opposite me.  Here’s a sketch of a vertical slice through the ball, and let’s begin on the left half of the diagram…Mirror ball sketch

I’m up there near the top, taking a picture with my phone.

To start with, we’ll put the LED (that yellow disk) at position A on the line running from top to bottom through the ball.  The blue lines trace the light path from the LED to me within this slice.

The inside of the ball is a mirror.  Whether flat or curved, the rule for every mirror is “The angle of reflection equals the angle of incidence.”  That’s how fun-house mirrors work.  You can see that the two solid blue lines form equal angles with the line tangent to the ball.  There’s no other point on this half-circle where the A-to-me route meets that equal-angle condition.  That’s why the blue line is the only path the light can take.  I’d see only one point of yellow light in that slice.

But the ball has a circular cross-section, like the Earth.  There’s a slice and a blue path for every longitude, all 360o of them and lots more in between.  Every slice shows me one point of yellow light, all at the same height.  The points all join together as a complete ring of light partway down the ball.  I’ve labeled it the “A-ring.”

Now imagine the ball moving upward to position B.  The equal-angles rule still holds, which puts the image of B in the mirror further down in the ball.  That’s shown by the red-lined light path and the labeled B-ring.

So far, so good — as the LED moves upward, I see a ring of decreasing size.  The surprise comes when the LED reaches C, the center of the ball.  On the basis of past behavior, I’d expect just a point of light at the very bottom of the ball (where it’d be on the other side of the LED and therefore hidden from me).

Nup, doesn’t happen.  Here’s the simulation.  The small yellow disk is the LED, the ring is the LED’s reflected image, the inset green circle shows the position of the LED (yellow) and the camera (black), and that’s me in the background, taking the picture…g6z

The entire surface suddenly fills with light — BLOOIE! — when the LED is exactly at the ball’s center.  Why does that happen?  Scroll back up and look at the right-hand half of the diagram.  When the ball is exactly at C, every outgoing ray of light in any direction bounces directly back where it came from.  And keeps on going, and going and going.  That weird display can only happen exactly at the center, the ball’s optical singularity, that special point where behavior is drastically different from what you’d expect as you approach it.

So that’s using geometry to identify a singularity.  When I built the model* that generated the video I had to do some fun algebra and trig.  In the process I encountered a deeper and more general way to identify singularities.

<Hint> Which direction did Newton avoid facing?

* – By the way, here’s a shout-out to Mathematica®, the Wolfram Research company’s software package that I used to build the model and create the video.  The product is huge and loaded with mysterious special-purpose tools, pretty much like one of those monster pocket knives you can’t really fit into a pocket.  But like that contraption, this software lets you do amazing things once you figure out how.

~~ Rich Olcott

And now for some completely different dimensions

On By rolcottIn Mathematics: Dimensions, Physics: Fundamentals, UncategorizedLeave a comment

Terry Pratchett wrote that Knowledge = Power = Energy = Matter = Mass.  Physicists don’t agree because the units don’t match up.

Physicists check equations with a powerful technique called “Dimensional Analysis,” but it’s only theoretically related to the “travel in space and time” kinds of dimension we discussed earlier.

Place setting LMTIt all started with Newton’s mechanics, his study of how objects affect the motion of other objects.  His vocabulary list included words like force, momentum, velocity, acceleration, mass, …, all concepts that seem familiar to us but which Newton either originated or fundamentally re-defined. As time went on, other thinkers added more terms like power, energy and action.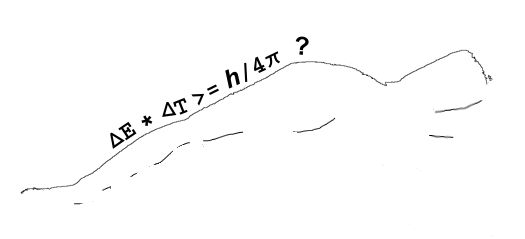

They’re all linked mathematically by various equations, but also by three fundamental dimensions: length (L), time (T) and mass (M). (There are a few others, like electric charge and temperature, that apply to problems outside of mechanics proper.)

Velocity, for example.  (Strictly speaking, velocity is speed in a particular direction but here we’re just concerned with its magnitude.)   You can measure it in miles per hour or millimeters per second or parsecs per millennium — in each case it’s length per time.  Velocity’s dimension expression is L/T no matter what units you use.

Momentum is the product of mass and velocity.  A 6,000-lb Escalade SUV doing 60 miles an hour has twice the momentum of a 3,000-lb compact car traveling at the same speed.  (Insurance companies are well aware of that fact and charge accordingly.)  In terms of dimensions, momentum is M*(L/T) = ML/T.

Acceleration is how rapidly velocity changes — a car clocked at “zero to 60 in 6 seconds” accelerated an average of 10 miles per hour per second.  Time’s in the denominator twice (who cares what the units are?), so the dimensional expression for acceleration is L/T2.

Physicists and chemists and engineers pay attention to these dimensional expressions because they have to match up across an equal sign.  Everyone knows Einstein’s equation, E = mc2. The c is the velocity of light.  As a velocity its dimension expression is L/T.  Therefore, the expression for energy must be M*(L/T)2 = ML2/T2.  See how easy?

Now things get more interesting.  Newton’s original Second Law calculated force on an object by how rapidly its momentum changed: (ML/T)/T.  Later on (possibly influenced by his feud with Leibniz about who invented calculus), he changed that to mass times acceleration M*(L/T2).  Conceptually they’re different but dimensionally they’re identical — both expressions for force work out to ML/T2.

Something seductively similar seems to apply to Heisenberg’s Area.  As we’ve seen, it’s the product of uncertainties in position (L) and momentum (ML/T) so the Area’s dimension expression works out to L*(ML/T) = ML2/T.

SeductiveThere is another way to get the same dimension expression but things aren’t not as nice there as they look at first glance.  Action is given by the amount of energy expended in a given time interval, times the length of that interval.  If you take the product of energy and time the dimensions work out as (ML2/T2)*T = ML2/T, just like Heisenberg’s Area.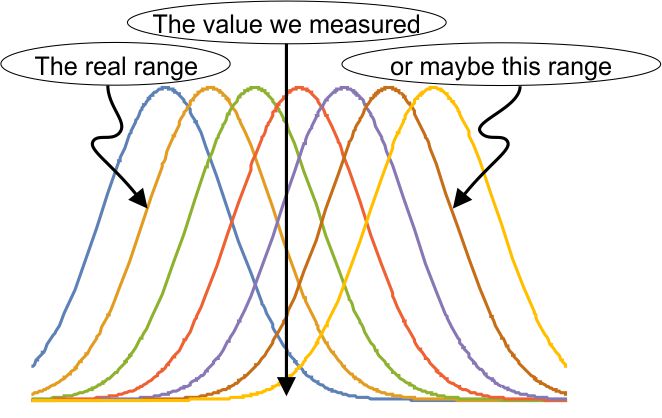

It’s so tempting to think that energy and time negotiate precision like position and momentum do.  But they don’t.  In quantum mechanics, time is a driver, not a result.  If you tell me when an event happens (the t-coordinate), I can maybe calculate its energy and such.  But if you tell me the energy, I can’t give you a time when it’ll happen.  The situation reminds me of geologists trying to predict an earthquake.  They’ve got lots of statistics on tremor size distribution and can even give you average time between tremors of a certain size, but when will the next one hit?  Lord only knows.

File the detailed reasoning under “Arcane” — in technicalese, there are operators for position, momentum and energy but there’s no operator for time.  If you’re curious, John Baez’s paper has all the details.  Be warned, it contains equations!

Trust me — if you’ve spent a couple of days going through a long derivation, totting up the dimensions on either side of equations along the way is a great technique for reassuring yourself that you probably didn’t do something stupid back at hour 14.  Or maybe to detect that you did.

~~ Rich Olcott

The Universe and Werner H.

On By rolcottIn Physics: Quantum Mechanics1 Comment

Heisenberg’s Area ( about 10-34 Joule-second) is small, one ten-millionth of the explosive action in a single molecule of TNT.  OK, that’s maybe important for sub-atomic physics, but it’s way too small to have any implications for anything bigger, right?  Well, it could be responsible for shaping our Universe.

Quick recap: The Heisenberg Uncertainty Principle (HUP) says that certain quantities (for instance, position and momentum) are linked in a remarkable way.  We can’t measure either of them perfectly accurately, but we can make repeated more-or-less sloppy measurements that give us average values.  The linkage is in that sloppiness.  Each repeated measurement lands somewhere in a range of values around the average.  HUP says that even with very careful measurement the product of those two spans must be greater than Heisenberg’s Area.

So now let’s head out to empty space, shall we?  I mean, really empty space, out there between the galaxies, where there’s only about one hydrogen atom per cubic meter.

Here’s a good cubic meter … sure enough, it’s got exactly one hydrogen atom in it.

g25For practice using Heisenberg’s Area, what can we say about the atom? (If you’re checking my math it’ll help to know that the Area, h/4π, can also be expressed as 0.5×10-34 kg m2/s; the mass of one hydrogen atom is 1.7×10-27 kg; and the speed of light is 3×108 m/s.)  On average the atom’s position is at the cube’s center.  Its position range is one meter wide.  Whatever the atom’s average momentum might be, our measurements would be somewhere within a momentum range of (h/4π kg m2/s) / (1 m) = 0.5×10-34 kg m/s. A moving particle’s momentum is its mass times its velocity, so the velocity range is (0.5×10-34 kg m/s) / (1.7×10-27 kg) = 0.3×10-7 m/s.

With really good tools we could determine the atom’s velocity within plus or minus 0.000 000 03 m/s.  Pretty good.

Now zoom in.  Dial that one-meter cube down a billion-fold to a nanometer (10-9 meters, which is still about ten times the atom’s width).  Yeah, the atom’s still in the box, but now its velocity range is 300 m/s.  The atom could be just hanging out at the center, or it could zoom out of the cube a microsecond after we looked — we just can’t tell which.

All of which illuminates the contrast between physics Newton-style and the physics that has bloomed since Einstein’s 1905 “miracle year.”  If Newton were in charge of the Universe, Heisenberg’s Area would be zero.  We could determine that atom’s position and momentum with complete accuracy.  In fact in principle we could accurately determine everything’s position and momentum and then calculate where everything would be at any time in the future.  But he isn’t and it’s not and we can’t.

Theorists and experimenters use the word “measurement” in different ways. A measurement done by a theoretician is generally based on fundamental constants and an Valueselaborate mathematical structure. If the measurement is a quantum mechanical result, part of that structure is our familiar bell-shaped curve.  It’s an explicit recognition that way down in the world of the very small, we can’t know what’s really going on.  Most calculations have to be statistical, predicting an average and an expected range about that average. That prediction may or may not pan out, depending on what the experimentalists find.

By contrast, when experimenters measure something, even as an average of multiple tests, it’s an estimate of the real distribution.  The research group (usually it’s a group these days) reports a distribution that they claim overlaps well with a real one out there in the Universe.  Then another group dives in to prove they or the theoreticians or both are wrong.  That’s how Science works.

You are hereSo there could be a collection of bell-curves gathered about the experimental result. Remember those extra dimensions we discussed earlier?  One theory that’s been floated is that along those extra dimensions the fundamental constants like h might take on different values.  Maybe further along “Dimension W” the value of h is bigger than it is in our Universe, and quantum effects are even more important than they are here.

Now how can we test that?

BTW, Heisenberg will be 114 on Dec 5.  Alles Gute zum Geburtstag, Werner!

~~ Rich Olcott

Heisenberg’s trade-offs

On By rolcottIn Physics: Quantum Mechanics, UncategorizedLeave a comment

KiteA kite floating on the breeze.  Optimal work-life balance.  Smoothly functioning free markets.  The Heisenberg Uncertainty Principle.  Why would an alien from another planet recognize the last one but maybe not the others?

The kite is a physical object, intentionally built by humans to human scale.  The next two are idealized theoretical constructs, goals to be approached but rarely achieved.  The Heisenberg Uncertainty Principle (HUP) is fundamental to how the Universe works.

The first three are each in a dynamic equilibrium that is constantly buffeted by competing forces.  The HUP comes straight out of the deep math for where those forces come from.  Kites and work stress and markets may be peculiar to Earth, but the HUP is in play on every planet and star.

In the last post we saw that thanks to the HUP we can precisely identify an oboe’s pitch if it plays forever.  We can know precisely when a pitchless cymbal crashed.  But it’s mathematically impossible to get both exact pitch and exact time for the same sound.  Thank goodness, we can have imprecise knowledge of both quantities and actually play some music.

We determine a pitch (cycles per second) by counting sound waves passing during a given duration — and that limits our knowledge.  We can’t know that a wave has passed unless we see at least two peaks.  Our observation period must be at least long enough to see two peaks.  To put it the other way, the pitch must be high enough to give us at least two peaks during the time we’re watching.  This isn’t quantum mechanics, it’s just arithmetic, but it’s basic to physics.

Mathematically the HUP is as simple as Einstein’s E=mc2 equation, except the HUP is an inequality:

[A-uncertainty] x [B-uncertainty] ≥ h / 4π

where A and B are two paired quantities like pitch and duration.

TNT(That h is Planck’s constant, “the quantum of action,” 6.6×10-34 joule-sec.  That’s a very small number indeed but it shows up everywhere in quantum physics.  To put h in scale, one gram of TNT packs 4184 joules of explosive energy.  TNT has a detonation velocity of 6900 meters/sec and density of 1.60 gram/cm3, so we can figure a 1-gram cube of the stuff would burn for 1.2 microseconds and generate a total action of about 5×10-3 joule-sec.  Divide that by Avagadro’s number to get that one molecule of TNT is good for 10-26 joule-sec.  That’s about 10 million times h.  So, yeah, h is small.)

Back to the HUP inequality.  A and B are our paired quantities.  The standard examples that everyone’s heard of are position and momentum, as in the old physicist joke, “I haven’t a clue where I’m going, but I know how fast I’m getting there.”  For things that are tied to a central attractor like an atomic nucleus, A and B would be angular position and angular momentum.  If you’re into solid-state physics you may have run into another example — the number of electrons in a superconducting current is paired with a metric that reflects the degree of order in the conducting medium.  One more pair is energy and time, but that’s a story for another week.

Balance 1But what’s in the HUP inequality isn’t A and B, but rather our uncertainty about each.  A billiard ball might be on the lip of the near cup or it can be all the way across the table — HUP won’t care.  What’s important to HUP is whether the ball is here plus/minus one inch, or here plus/minus a millionth of an inch.  Similarly, HUP doesn’t care how fast the ball is going, but it does care whether the speed is plus/minus one inch per second or plus/minus one millionth of an inch per second.  HUP tells us that we can know one of the pair precisely and the other not at all, or that we can know both imprecisely.  Furthermore, even the imprecision has a limit.

We can’t simultaneously know both A and B more precisely than that little teeny h, but some physicists believe h may have been big enough to launch our Universe.

Next week — HUP, two, three, four

~~ Rich Olcott