A December nip’s in the air. I’m in my office trying to persuade the heating system to be more generous, when Vinnie wanders in carrying a magazine. “I been reading about how a pound won’t be a pound any more.”
This takes me a moment to work out. “Ah, you’re talking kilograms, not pounds, right?”
“Pound, kilogram, same difference, they’re both weights.”
“No, they’re not. A kilogram at the bottom of the sea would still be a kilogram at the top of a mountain, but a pound high up weighs less than a pound lower down.”
“In what alternate universe does that make sense?”
“In any universe where Galileo’s observations and Newton’s equations are valid. Thanks to them we know the difference between weight and mass.”
“Which is…?”
“That’s where things get subtle and it took Newton to tease them apart. It’s the difference between quantifying something with a spring scale and quantifying it with a balance. Say you put a heavy object on a scale. It pulls down on the spring and the spring pulls up on the object. When everything stops moving, the upward and downward forces are equal. Given the spring’s stretch-per-pound relationship, you can measure the stretch and figure out how many pounds of force the object exerts.”
“Yeah, so…?”
“So now you put the same object on one pan of a balance. You put kilogram blocks on the other pan until the balance beam levels out. The beam goes level because the two sides of the balance carry the same mass. Count the blocks and you know your object’s mass in kilograms.”
“Like I said, same difference.”
“Nope, because you’ve done two different operations. On a balance your object will match up with the same number of blocks wherever you go with them. Balance measurements are all about mass. With the spring scale you compared gravity’s force against some other kind of force. If you go somewhere else where gravity’s weaker, say to the top of Mt Everest, the scale will show a different weight even though the mass hasn’t changed.”
“How much different?”
“Not much for most purposes — about two pounds per ton between sea-level and Mt Everest’s peak. But that’s a huge variation for physicists who look for clues to the Universe in the 5th or 6th decimal place. High tech science and engineering need measurements, like mass, that are precise, stable and reproducible in many labs. You noticed that both of my example measurements are too approximate for the techs.”
“Sure, the scale thing can be off because the spring can get wonky with use. Um, and you can only measure the stretch within a percent or so probably. But you can count the kilogram blocks — that ought to be a pretty good number.”
“Count-based metrics are indeed the most precise, but they’re problematic in their own way. For one thing, maybe the object isn’t an exact number of kilograms. Best you can do is say it’s between n and n+1 kilograms. But it’s worse than that. The kilogram blocks can get wonky, too — finger-marks, corrosion, all of that.”
“But you can counter that by comparing the daily-use blocks with a standard you don’t use much.”
“Which sooner or later gets wonky with use so you have re-calibrate it to a whole chain of calibration blocks going back to a lovingly preserved great-grandmaster standard block, but what do we do when we get to Mars where it’d be difficult to get the local standard back to Earth for a re-calibration?”
“I see the problem. Is that why a kilogram won’t be a kilogram any more?”
“Well, that’s why The Kilogram won’t be Le grand K, the great-grandmaster standard — a carefully monitored hunk of platinum-iridium that’s actually kept in a guarded, climate-controlled vault in a Paris basement. It’s taken out only once every few years to compare with its kin. Even so it appears to have lost 50 micrograms since 1889. We think. So they’re demoting it.”
“What’re they replacing it with? Not another lump of metal, then?”
“Oh, no, they need something that’s precisely reproducible anywhere, preferably something that’s count-based. The new standard will be official soon. It’s a great physics story.”
~~ Rich Olcott
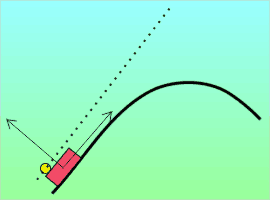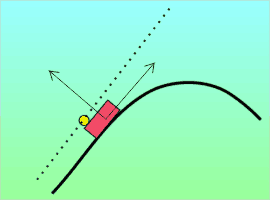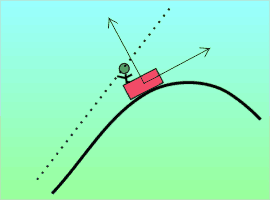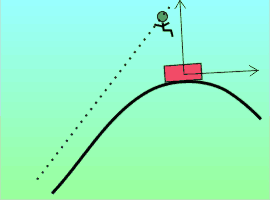But there are other accelerations that aren’t so easily accounted for. Ever ride in a car going around a curve and find yourself almost flung out of your seat? This little guy wasn’t wearing his seat belt and look what happened. The car accelerated because changing direction is an acceleration due to a lateral force. But the guy followed Newton’s First Law and just kept going in a straight line. Did he accelerate?
Suppose you’re investigating an object’s motion that appears to arise from a new force you’d like to dub “heterofugal.” If you can find a different frame of reference (one not attached to the object) or otherwise explain the motion without invoking the “new force,” then heterofugalism is a fictitious force.
Hard Science Ain't Hard 