Last week we introduced the tesseract, which is to a cube what a cube is to a square — an extension into one more dimension. That’s why it’s also called a hypercube. The first tesseract diagrams I ever saw were so confusing — they looked like lots of overlapped squares tied together with lines that didn’t make much sense. I wondered, “Wouldn’t it be easier to understand a tesseract if I could see it rotating?”
Years later computers and I had both moved ahead to where I could generate the pictures you see in this post. What I learned while doing that was that 4-D figures have two equators. In four dimensions, it’s possible for something to rotate in two perpendicular directions at the same time. Read on and please don’t mind my doggerel — it doesn’t bite.
In the 4-D views, when one of the tesseract’s cubical faces appears to disappear into an adjacent face, what’s actually happening is that the face is sliding past the other face along that fourth dimension (which I called W because why not?)
You’re looking at a two-dimensional picture of the three-dimensional projection of a four-dimensional object as it moves in 5-space (X, Y, Z, W, and time — if it didn’t move in time then it couldn’t be spinning).
Next week — Herr Klein’s bottle, or rather flask, or rather surface.
~~ Rich Olcott




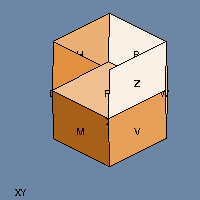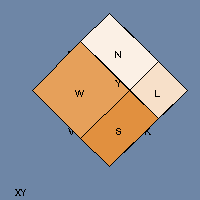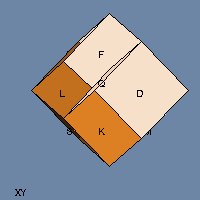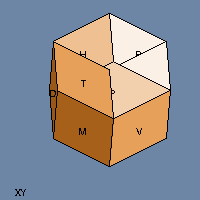
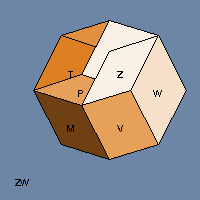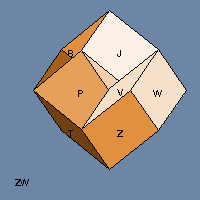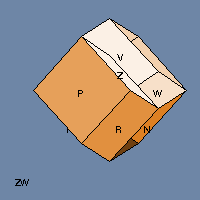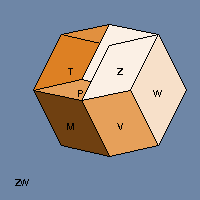

To grok 4(5)-D in 2 is too much of a stretch. Please make a 3(4)-D model…
LikeLike
I’ll work on that — but it won’t spin.
LikeLike
I like ’em. Here’s the rub for me. The shows I’ve watched discussing string theory for us masses generally mention that those additional 8+ dimensions are tiny, and even, if I remember correctly, transient. Here’s a potential future topic for you: How the heck is a dimension tiny, much less transient?
LikeLike
That’s on the list, but there are a couple of other topics already workin’. Stay tuned.
LikeLike