A familiar footstep in the hall outside my office. “Door’s open, Vinnie, c’mon in.”

“Hi, Sy. Brought you something.” <lays a card on my desk> “So the question is, what’s the area inside the semicircle?”

<thoughtful pause> “Zero.”

“Dang, that’s both you and Larry say it’s zero. I don’t see it. ‘Splain, okay?”

“Larry gave you this?’

“Yeah. Can’t be zero area, it’s right there all spread out. How do you figure zero?”

“Start with the diagonal lines. The ‘a‘ line has a length of one unit, right?”

“The picture says so, but what’s i about on line ‘b‘?”

“That’s a special number, defined to be the solution x of the equation x²+1=0. Taking square roots, x=i and i²+1=0. I know you hate equations, but bear with me.”

<grumble> “Okay, go ahead.”

“If we had the radius r, the area would be ½πr². Line c is the diameter so the radius is r=c/2. We can get c by solving the triangle. We know it’s a right triangle because all three vertices touch a semicircle, right?”

“Geometry I remember; it was algebra gave me fits.”

“Then you remember good old Pythagoras and his a²+b²=c² formula, which we can use here because it’s a right triangle. Plugging in the known lengths we get c²=1²+i²=i²+1. Look familiar?”

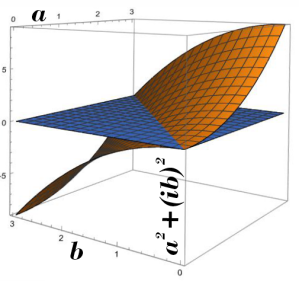
“Yeahhh, i²+1=0 from the definition so c² is zero. What if b was 3?”

“We’d have c²=1²+(3i)²=1+9i²=1–9=–8. If both a and b are 3, then c²=3²+(3i)²=9+9i²=9–9 and we’re back to c²=0. It’s just arithmetic, but enhanced with i and its special rules.”

“Wait. If c²=0 then c=0 and c‘s the diameter and if that’s zero then so’s the radius and the area. The whole thing shrinks to a point but it can’t ’cause it’s right there spread out in the picture. Is this sort of thing why they told us x²–1=0 has a solution but x²+1=0 doesn’t?”

“It’s closely related, because i is involved. Incidentally, they lied to you in that algebra class. They showed you that famous quadratic equation ax²+bx+c=0, right, along with the magic b²–4ac formula. If that formula is positive you’ve got two roots, they said, but if it’s negative there’s no root.”

“Sounds familiar. Where’s the lie?”

“The first part’s true: with x²–1=0 you’ve got a=1,b=0,c=–1 with two roots x=1 and x=–1. The lie is in the second part: with x²+1=0 you’ve got a=1,b=0,c=+1 with two roots x=i and x=–i. All of those are perfectly good solutions.”

“But i‘s not a number! I can’t have i apples and I can’t write a check for i dollars. Why even play with it?”

“The i‑numbers are numbers, just not counting numbers. They’ve been part of mainstream math ever since the early Renaissance. Algebra was almost a blood sport at the time. Academics in Italy used to issue public challenges to solve problems that they’d already solved secretly. There were duels to settle questions of priority. Bombelli systematized i‑number arithmetic while working out one limited class of cubic equations. Cardano compiled solutions from multiple authors, including Bombelli, into his book Ars Magna. Then he systematically added his own solutions to a catalog of cubic and quartic equations. The Old Guard refused to believe in either i‑numbers or negative numbers, but Cardano showed you can’t escape them if you’re doing serious algebra.”

“Not even negative numbers?”

“Nope. The negatives weren’t widely accepted until the Venetian trading houses forced the issue — negatives are implicit in the merchants’ newly‑invented double‑entry bookkeeping. i‑numbers weren’t considered respectable for hundreds of years.”

“Then what happened?”

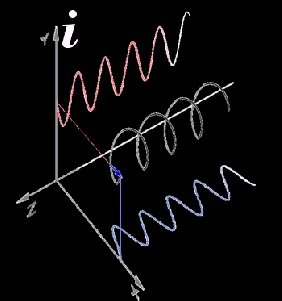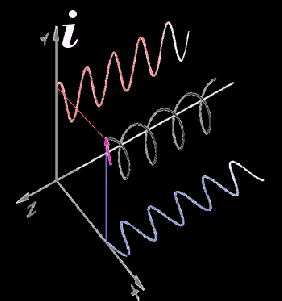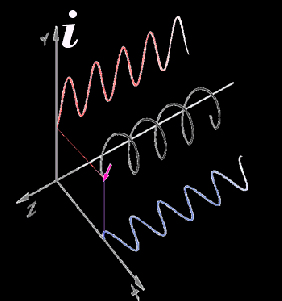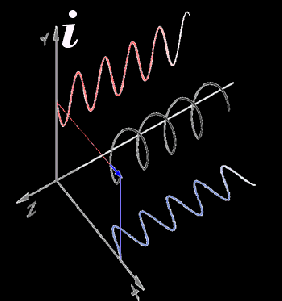
“Several advances. Euler connected i with trigonometry. Add Descarte‘s coordinate system, Fourier‘s wave analysis and Leibniz‘ notational innovations. For example, plotting an i‑number helix in 3D gives you these sine waves. When I think ‘i‑axis‘ I think ‘perpendicular to other coordinates‘.”

“Like Las Vegas.”

“Similar.”

• Thanks to Lloyd Boyer who raised several good points.

~~ Rich Olcott