It’s been a while since I heard that footstep in the hall outside my office. “Door’s open, Vinnie, c’mon in.”

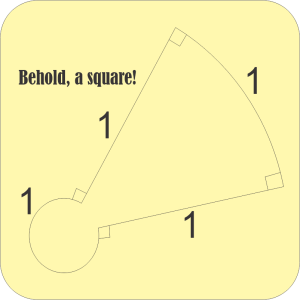
“Hi, Sy. Brought you a thing.” <lays a card on my desk> “So the question is, how is this a square?”

“Is this another puzzle you got from Larry?”

“Yeah. He said you could ‘splain it.”

“Well, the idea’s clear — four right angles, four equal sides, sounds square-ish to me.”

“Yeah, but is the picture lying to us the way that other one did?”

“Fair question. Let’s see whether we can construct it with some real numbers. Both of those arcs seem to be parts of concentric circles so I’ll assume that.” <drawing on card> “The one that’s most of a circle has a radius I’ll call r.”

“You’re gonna do equations, ain’t you? You know I hate equations.”

“You asked the question. Bear with me, this won’t take long. Those two straight lines seem to run radially out from the almost‑circle’s center. I’ll call the angle between them a. By the way, if the lines are indeed radial then we’re guaranteed that all four of those ‘right angle’ markers are truthful. Any radius meets its circumference in a right angle, right?”

“Learned that in Geometry class.”

“I certainly hope so. Okay, the radius of the outer arc is 1 plus the radius of the inner arc so the length of the outer arc is the angle times that or a(1+r) —”

“Wait, where did that come from? You can’t just multiply the angle and radius together like that.”

“Sure you can. What’s the formula for a circle’s circumference?”

“2πr.”

“Which is an angle, 2π, times the radius.”

“How is 2π an angle? Should be 360°.”

“It’s like feet and meters ‑ same value, different units. Physicists like radians. 180° is π radians and the length of a semicircle is πr. Other arcs work the same way. It’s perfectly legal to multiply angle and radius if you express the angle in radians. So that outer arc length is a(1+r) and that’s 1 according to the diagram. Are you with me?”

“I suppose.”

“Now for the almost‑circle. Its angle is 2π minus that bit that got stretched out. Are we agreed that the arc length is (2π-a)r?”

“And that’s also 1.”

“Right. So we have two unknowns a and r, and two equations to settle them with: a(1+r)=1 and (2π-a)r=1. Simple high school algebra but I’ll spare you the pain and just ask Old Reliable for the result.”

“Thank you.”

“So there’s your answer. Yes, the keyhole figure can be truthful if the angle is 48.4° and the sticky‑out part is about 5½ times longer than the almost‑circle’s radius. Any other angle or radius and the diagram’s wrong. Happy?”

“Yeah.” <quiet moment> “Hey, I just figured out a different way. The latitude lines and longitude lines always cross at right angles, right?”

“Right.”

“So you could do a keyhole ‘square’ on the Earth, right? Circle the North Pole at some latitude, except take a detour straight south, then straight west for a while, then straight back north just in time to meet your part‑circle’s starting point. I’ve flown crazy routes a little like that but that’s always been point‑to‑point. How do you from‑scratch figure something like that so that all the sides are the same length?”

“Whoa, that’s a much harder problem. You’re flying over Earth’s surface so r is constant but now you’ve got two angular variables, latitude and longitude. The north‑south tracks are pretty straight‑forward — you’re good if one starts at the same latitude the other stops at. The tough part is how to split the 360° of longitude between the two east‑west tracks so that the southern arc is the same length as the northern one and they both match the north‑south distance which depends on the start‑stop latitudes. That’s not quadratic equations any more, we’re looking at transcendental equations involving trig functions. There may not be a closed‑form solution. To get those angles we’d need a load of computer time doing successive approximations toward a numerical solution. Surely keyhole‑square routes exist but they’re well‑hidden.”

“Regular squares’re much easier. Colorado or Wyoming’d be no problem.”

~~ Rich Olcott