Cathleen and I are sharing scones and memories when Vinnie trundles up to our table. “Glad I got you two together. I just ran across a couple news items and I need some explanations.”

“Astronomy AND Physics in the same news items? Do tell.”

“They’re only one paragraph each and read like someone wrote ’em before their morning coffee. They’re both about that big black hole they’ve been taking pictures of.”

“The one in our galaxy or the M87* supermassive black hole in the Messier‑87 galaxy?”

“The second one, Cathleen. This item says it shot out a jet traveling faster than light.”

<sigh> “Pop‑sci journalism at its worst, right, Sy? I know the work that’s based on and the academic reports don’t say that. Good observations leading to less flamboyant conclusions.”

“Maybe it was supposed to be a bigger article but the editors cut it down badly. That happens. I’m sure it’s not really a superluminal jet—”

“Superluminal’s faster‑than‑light, right?”

“Right, Vinnie. Sorry to get technical. Anyway, it’s an illusion.”

“Ah geez, it’ll be frames again, right?” <eyes suddenly open wide> “Wait, I got it! I betcha it’s about the time difference. Take a blob in that jet, it’s flying out at near lightspeed. Time dilation happens when relativity’s in the game, me and Sy talked about that, so blob‑frame seconds look like they take longer than ours do. We see the blob cramming a lightsecond of distance traveled into less than one of our seconds and that’s superluminal. Am I right, Sy?”

“Right answer to a different question, I’m afraid. You’re straight on the time dilation but it doesn’t apply to this situation. Something happening within the blob’s frame, maybe a star blowing up or something weird metabolizing in there, Special Relativity’s time distortion hijinks would show us that action taking place in slow motion. But this superluminal blob claim hinges on how the blob’s whole frame moves relative to ours. That motion isn’t superluminal but it can look that way if conditions are right. As I understand it, the M87* jet qualifies. Your bailiwick rather than mine, Cathleen.”

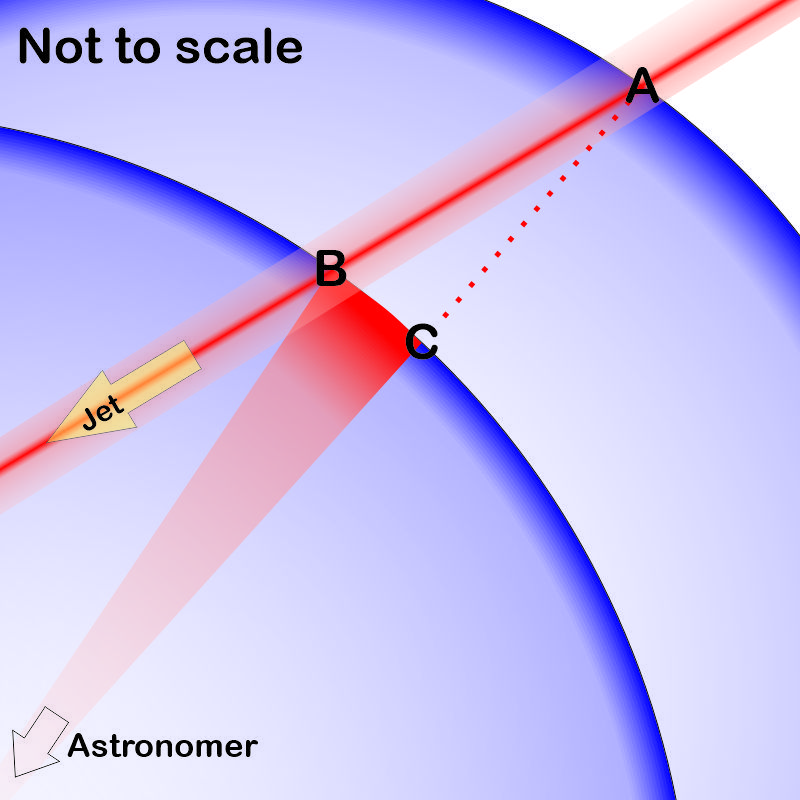
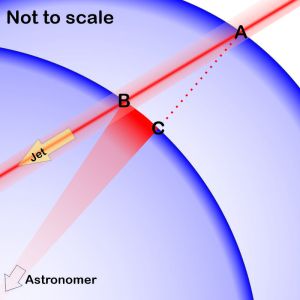
“Actually it is a frames thing, Vinnie, but timeframes, not spacetime. Those blobs move too slowly in our sky to watch in real time. We take snapshot A and then maybe a few years later we take snapshot B and compare. Speed is the ratio of distance to time. We need the A‑B distance in 3‑D space to compare to the known time between snapshots. But we can’t see the blob’s trajectory in 3‑D. All we can capture is its 2‑D arc C‑B across an imaginary spherical shell we call the sky. If the M87* jet were perpendicular to our line of sight the C‑B image on the sky‑sphere would match the 3‑D path. Multiply the image’s angle in radians by the distance to M87* and we’re done.”

“We’re not done?”

“Nope. This jet points only 20° away from our direct line of sight. I’ll spare you the trigonometry and just say that distance A‑B is about 3 times longer than C‑B.”

“So we measure C‑B, triple the angle and multiply by the M87* distance. No problem.”

“Problem. That tripling is what makes the blob’s A‑B journey appear to go faster than light. Three times 0.4c equals 1.2c. But you missed something important. Your arithmetic assumed you could use a simple ‘M87* distance’. Not in this case, because the blob moves towards us at close to lightspeed. Visualize two concentric sky‑spheres. The outer one’s radius runs from us to the blob’s location at A‑time. The inner sphere’s radius runs to the blob’s location at B‑time. The B‑sphere is our reference frame. The light we saw at A‑time had to travel from the outer sphere to the inner one before we could register the C‑B image.”

“Can’t be very far.”

“We’re talking years at lightspeed, so lightyears, so significant. A properly illusion‑free A‑B travel calculation must include the A‑C travel time in the denominator of the distance/time ratio. The true kilometers per second come out well below lightspeed. Oh, and relativity’s not involved.”

“Dang, Cathleen, it was such a cool illusion.”

~ Rich Olcott