Category: Mathematics: Dimensions

Calvin And Hobbes And i

On By rolcottIn General: Fun Stuff, Mathematics: Dimensions, UncategorizedLeave a comment

Hobbes 2I so miss Calvin and Hobbes, the wondrous, joyful comic strip that cartoonist Bill Watterson gave us between 1985 and 1995.  Hobbes was a stuffed toy tiger — except that 6-year-old Calvin saw him as a walking, talking man-sized tiger with a sarcastic sense of humor.

So many things in life and physics are like Hobbes — they depend on how you look at them.  As we saw earlier, a fictitious force disappears when viewed from the right frame of reference.  There’s that particle/wave duality thing that Duc de Broglie “blessed” us with.  And polarized light.

In an earlier post I mentioned that light is polar, in the sense that a single photon’s electric field acts to vibrate an electron (pole-to-pole) within a single plane.
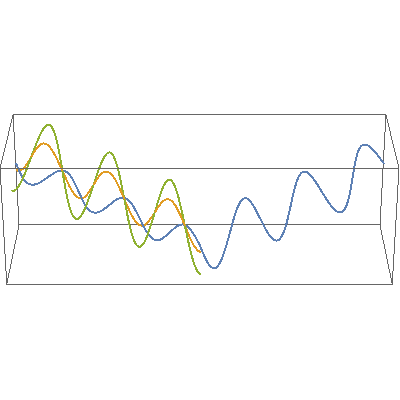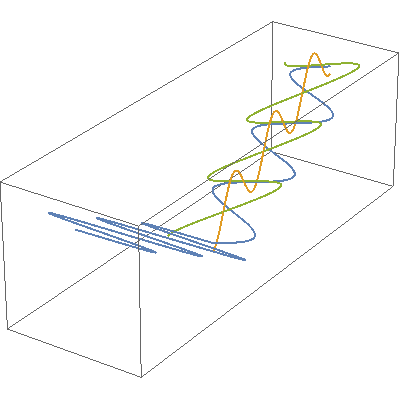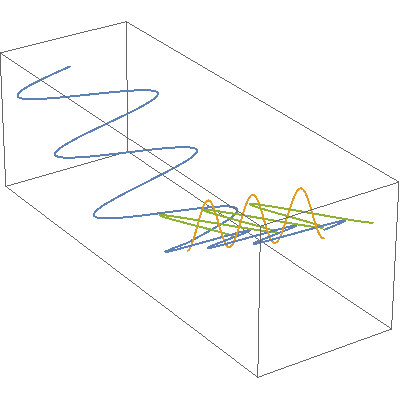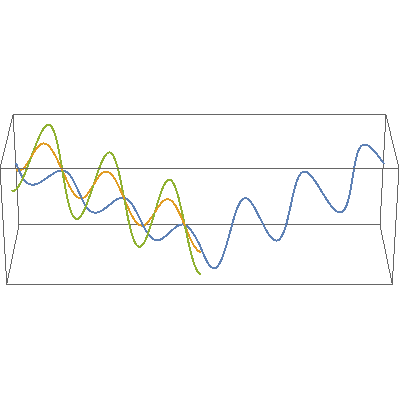wavesIn this video, orange, green and blue electromagnetic fields shine in from one side of the box onto its floor.  Each color’s field is polar because it “lives” in only one plane.  However, the beam as a whole is unpolarized because different components of the total field direct recipient electrons into different planes giving zero net polarization.  The Sun and most other familiar light sources emit unpolarized light.

When sunlight bounces at a low angle off a surface, say paint on a car body or water at the beach, energy in a field that is directed perpendicular to the surface is absorbed and turned into heat energy.  (Yeah, I’m skipping over a semester’s-worth of Optics class, but bear with me.)  In the video, that’s the orange wave.

At the same time, fields parallel to the surface are reflected.  That’s what happens to the blue wave.

Suppose a wave is somewhere in between parallel and perpendicular, like the green wave.  No surprise, the vertical part of its energy is absorbed and the horizontal part adds to the reflection intensity.  That’s why the video shows the outgoing blue wave with a wider swing than its incoming precursor had.

The net effect of all this is that low-angle reflected light is polarized and generally more intense than the incident light that induced it.  We call that “glare.”  Polarizing sunglasses can help by selectively blocking horizontally-polarized electric fields reflected from water, streets, and that *@%*# car in front of me.

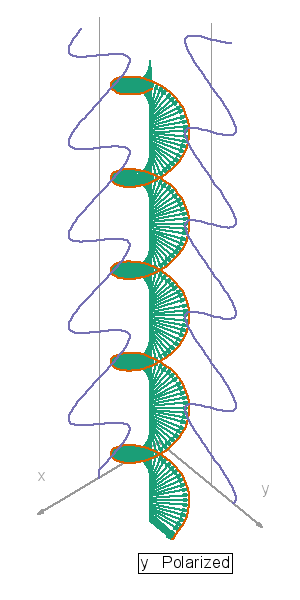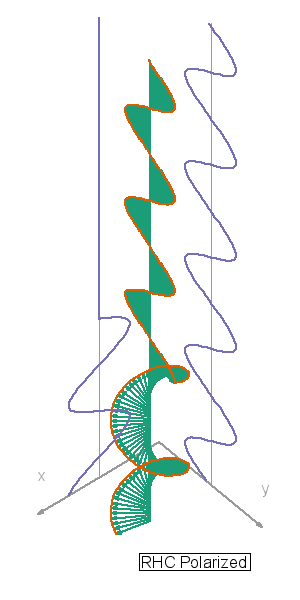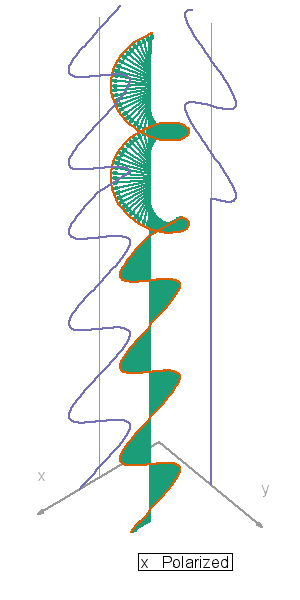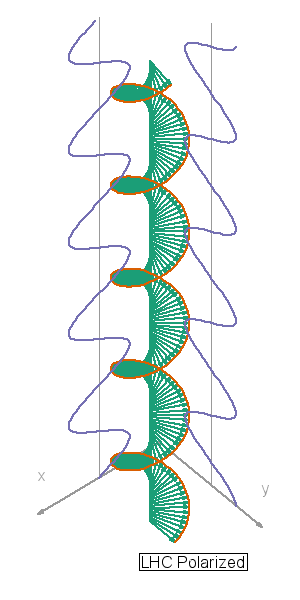
Wave_Polarisation
David Jessop’s brilliant depiction of plane and circularly polarized light

Things can get more complicated. The waves in the first video are all in synch — their peaks and valleys match up (mostly). But suppose an x-directed field and a y-directed field are headed along the same course.  Depending on how they match up, the two can combine to produce a field driving electrons along the x-direction, the y-direction, or in clockwise or counterclockwise circles.  Check the red line in this video — RHC and LHC depict the circularly polarized light that sci-fi writers sometimes invoke when they need a gimmick.

Physicists have several ways to describe such a situation mathematically.  I’ve already used the first, which goes back 380 years to René Descartes and the Cartesian x, y,… coordinate system he planted the seed for.  We’ve become so familiar with it that reading a graph is like reading words.  Sometimes easier.

In Cartesian coordinates we write x– and y-coordinates as separate functions of time t:
x = f1(t)
y = f2(t)
where each f could be something like 0.7·t2-1.3·t+π/4 or whatever.  Then for each t-value we graph a point where the vertical line at the calculated x intersects the horizontal line at the calculated y.

But we can simplify that with a couple of conventions.  Write √(-1) as i, and say that i-numbers run along the y-axis.  With those conventions we can write our two functions in a single line:
x + i y = f1(t) + i f2(t)
One line is better than two when you’re trying to keep track of a big calculation.

But people have a long-running hang-up that’s part theory and part psychology.  When Bombelli introduced these complex numbers back in the 16th century, mathematicians complained that you can’t pile up i thingies.  Descartes and others simply couldn’t accept the notion, called the numbers “imaginary,” and the term stuck.

Which is why Hobbes the way Calvin sees him is on the imaginary axis.

~~ Rich Olcott

Is cyber warfare imaginary?

On By rolcottIn General: Fun Stuff, Mathematics: Dimensions, UncategorizedLeave a comment

Rule One in hooking the reader with a query headline is: Don’t answer the question immediately.  Let’s break that one.  Yes, cyber warfare is imaginary, but only for a certain kind of “imaginary.”  What kind is that, you ask.  AaaHAH!

spy1
Antonio Prohías’ Mad Magazine spies
didn’t normally use cyber weaponry

It all has to do with number lines.  If the early Greek theoreticians had been in charge, the only numbers in the Universe would have been the integers: 1, 2, 3,….  Life is simple when your only calculating tool is an abacus without a decimal point.  Zero hadn’t been invented in their day, nor had negative numbers.

Then Pythagoras did his experiments with harmony and harp strings, and the Greeks had to admit that ratios of integers are rational.

More trouble from Pythagoras: his a2+b2=c2 equation naturally led to c=√(a2+b2).  Unfortunately, for most integer values of a and b, c can’t be expressed as either an integer or a ratio of integers.  The Greeks labeled such numbers (including π) as irrational and tried to ignore them.

Move ahead to the Middle Ages, after Europe had imported zero and the decimal point from Brahmagupta’s work in India, and after the post-Medieval rise of trade spawned bookkeepers who had to cope with debt.  At that point we had a continuous number line running from “minus a whole lot” to “plus you couldn’t believe” (infinity wasn’t seriously considered in Western math until the 17th century).

By then European mathematicians had started playing around with algebraic equations and had stumbled into a problem.  They had Brahmagupta’s quadratic formula (you know, that [-b±√(b2-4a·c)]/2a thing we all sang-memorized in high school).  What do you do when b2 is less than 4a·c and you’re looking at the square root of a negative number?

Back in high school they told us, “Well, that means there’s no solution,” but that wasn’t good enough for Renaissance Italy.  Rafael Bombelli realized there’s simply no room for weird quadratic solutions on the conventional number line.  He made room by building a new number line perpendicular to it.  The new line is just like the old one, except everything on it is multiplied by i=√(-1).

(Bombelli used words rather than symbols, calling his creation “plus of minus.”  Eighty years later, René Descartes derisively called Bombelli’s numbers “imaginary,” as opposed to “real” numbers, and pasted them with that letter i.  Those labels have stuck for 380 years.  Except for electricity theoreticians who use j instead because i is for current.)

AxesSuppose you had a graph with one axis for counting animal things and another for counting vegetable things.  Animals added to animals makes more animals; vegetables added to vegetables makes more vegetables.  If you’ve got a chicken, two potatoes and an onion, and you share with your buddy who has a couple of carrots, some green beans and another onion, you’re on your way to a nice chicken stew.

Needs salt, but that’s on yet another axis.

Bombelli’s rules for doing arithmetic on two perpendicular number lines work pretty much the same.  Real numbers added to reals make reals, imaginaries added to imaginaries make more imaginaries.  If you’ve got numbers like x+i·y that are part real and part imaginary, the separate parts each follow their own rule.  Multiplication and division work, too, but I’ll let you figure those out.

The important point is that what happens on each number line can be specified independently of what happens on the other, just like the x and y axes in Descartes’ charts.  Together, Bombelli’s and Descartes’ concepts constitute a nutritious dish for physicists and mathematicians.

Scientists love to plot different experimental results against each other to see if there’s an interesting relationship in play.  For certain problems, for example, it’s useful to plot real-number energy of motion (kinetic energy) against some other variable on the i-axis.

Two-time Defense Secretary Donald Rumsfeld used to speak of “kinetic warfare,” where people get killed, as opposed to the “non-kinetic” kind.  Apparently, he would have visualized cyber somewhere up near the i-axis.  In that scheme, cyber warriors with their ones and zeros are Bombelli-imaginary even if they’re real.

 ~~ Rich Olcott

 

Throwing a Summertime curve

On By rolcottIn Cosmology, Mathematics: Dimensions, Physics: Black Holes and Relativity, UncategorizedLeave a comment

All cats are gray in the dark, and all lines are straight in one-dimensional space.  Sure, you can look at a garden hose and see curves (and kinks, dammit), but a short-sighted snail crawling along on it knows only forward and backward.  Without some 2D notion of sideways, the poor thing has no way to sense or cope with curvature.

Up here in 3D-land we can readily see the hose’s curved path through all three dimensions.  We can also see that the snail’s shell has two distinct curvatures in 3D-space — the tube has an oval cross-section and also spirals perpendicular to that.

But Einstein said that our 3D-space itself can have curvature.  Does mass somehow bend space through some extra dimension?  Can a gravity well be a funnel to … somewhere else?

No and no.  Mathematicians have come up with a dozen technically different kinds of curvature to fit different situations.  Most have to do with extrinsic non-straightness, apparent only from a higher dimension.  That’s us looking at the hose in 3D.

Einstein’s work centered on intrinsic curvature, dependent only upon properties that can be measured within an object’s “natural” set of dimensions.Torus curvature

On a surface, for instance, you could draw a triangle using three straight lines.  If the figure’s interior angles sum up to exactly 180°, you’ve got a flat plane, zero intrinsic curvature.  On a sphere (“straight line” = “arc from a great circle”) or the outside rim of a doughnut, the sum is greater than 180° and the curvature is positive.
Circle curvatures
If there’s zero curvature and positive curvature, there’s gotta be negative curvature, right?  Right — you’ll get less-than-180° triangles on a Pringles chip or on the inside rim of a doughnut.

Some surfaces don’t have intersecting straight lines, but you can still classify their curvature by using a different criterion.  Visualize our snail gliding along the biggest “circle” he/she/it (with snails it’s complicated) can get to while tethered by a thread pinned to a point on the surface. Divide the circle’s circumference by the length of the thread.  If the ratio’s equal to 2π then the snail’s on flat ground.  If the ratio is bigger than 2π,  the critter’s on a saddle surface (negative curvature). If it’s smaller, then he/she/it has found positive curvature.

In a sense, we’re comparing the length of a periphery and a measure of what’s inside it.  That’s the sense in which Einsteinian space is curved — there are regions in which the area inside a circle (or the volume inside a sphere) is greater than or less than what would be expected from the size of its boundary.

Here’s an example.  The upper panel’s dotted grid represents a simple flat space being traversed by a “disk.”  See how the disk’s location has no effect on its size or shape.  As a result, dividing its circumference by its radius always gives you 2π.Curvature 3

In the bottom panel I’ve transformed* the picture to represent space in the neighborhood of a black hole (the gray circle is its Event Horizon) as seen from a distance.  Close-up, every row of dots would appear straight.  However, from afar the disk’s apparent size and shape depend on where it is relative to the BH.

By the way, the disk is NOT “falling” into the BH.  This is about the shape of space itself — there’s no gravitational attraction or distortion by tidal spaghettification.

Visually, the disk appears to ooze down one of those famous 3D parabolic funnels.  But it doesn’t — all of this activity takes place within the BH’s equatorial plane, a completely 2D place.  The equations generate that visual effect by distorting space and changing the local distance scale near our massive object.  This particular distortion generates positive curvature — at 90% through the video, the disk’s C/r ratio is about 2% less than 2π.

As I tell Museum visitors, “miles are shorter near a black hole.”

~~ Rich Olcott

* – If you’re interested, here are the technical details.  A Schwarzchild BH, distances as multiples of the EH radius.  The disk (diameter 2.0) is depicted at successive time-free points in the BH equatorial plane.  The calculation uses Flamm’s paraboloid to convert each grid point’s local (r,φ) coordinates to (w,φ) to represent the spatial configuration as seen from r>>w.

Reflections in Einstein’s bubble

On By rolcottIn Mathematics: Dimensions, Physics: Black Holes and Relativity, Physics: Light and Relativity, Physics: Quantum Mechanics, UncategorizedLeave a comment

There’s something peculiar in this earlier post where I embroidered on Einstein’s gambit in his epic battle with Bohr.  Here, I’ll self-plagiarize it for you…

Consider some nebula a million light-years away.  A million years ago an electron wobbled in the nebular cloud, generating a spherical electromagnetic wave that expanded at light-speed throughout the Universe.

Last night you got a glimpse of the nebula when that lightwave encountered a retinal cell in your eye.  Instantly, all of the wave’s energy, acting as a photon, energized a single electron in your retina.  That particular lightwave ceased to be active elsewhere in your eye or anywhere else on that million-light-year spherical shell.

Suppose that photon was yellow light, smack in the middle of the optical spectrum.  Its wavelength, about 580nm, says that the single far-away electron gave its spherical wave about 2.1eV (3.4×10-19 joules) of energy.  By the time it hit your eye that energy was spread over an area of a trillion square lightyears.  Your retinal cell’s cross-section is about 3 square micrometers so the cell can intercept only a teeny fraction of the wavefront.  Multiplying the wave’s energy by that fraction, I calculated that the cell should be able to collect only 10-75 joules.  You’d get that amount of energy from a 100W yellow light bulb that flashed for 10-73 seconds.  Like you’d notice.

But that microminiscule blink isn’t what you saw.  You saw one full photon-worth of yellow light, all 2.1eV of it, with no dilution by expansion.  Water waves sure don’t work that way, thank Heavens, or we’d be tsunami’d several times a day by earthquakes occurring near some ocean somewhere.

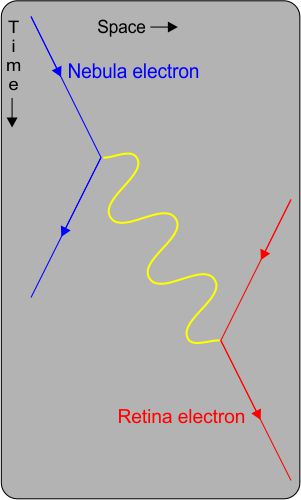Feynman diagramHere we have a Feynman diagram, named for the Nobel-winning (1965) physicist who invented it and much else.  The diagram plots out the transaction we just discussed.  Not a conventional x-y plot, it shows Space, Time and particles.  To the left, that far-away electron emits a photon signified by the yellow wiggly line.  The photon has momentum so the electron must recoil away from it.

The photon proceeds on its million-lightyear journey across the diagram.  When it encounters that electron in your eye, the photon is immediately and completely converted to electron energy and momentum.

Here’s the thing.  This megayear Feynman diagram and the numbers behind it are identical to what you’d draw for the same kind of yellow-light electron-photon-electron interaction but across just a one-millimeter gap.

It’s an essential part of the quantum formalism — the amount of energy in a given transition is independent of the mechanical details (what the electrons were doing when the photon was emitted/absorbed, the photon’s route and trip time, which other atoms are in either neighborhood, etc.).  All that matters is the system’s starting and ending states.  (In fact, some complicated but legitimate Feynman diagrams let intermediate particles travel faster than lightspeed if they disappear before the process completes.  Hint.)

Because they don’t share a common history our nebular and retinal electrons are not entangled by the usual definition.  Nonetheless, like entanglement this transaction has Action-At-A-Distance stickers all over it.  First, and this was Einstein’s objection, the entire wave function disappears from everywhere in the Universe the instant its energy is delivered to a specific location.  Second, the Feynman calculation describes a time-independent, distance-independent connection between two permanently isolated particles.  Kinda romantic, maybe, but it’d be a boring movie plot.

As Einstein maintained, quantum mechanics is inherently non-local.  In QM change at one location is instantaneously reflected in change elsewhere as if two remote thingies are parts of one thingy whose left hand always knows what its right hand is doing.

Bohr didn’t care but Einstein did because relativity theory is based on geometry which is all about location. In relativity, change here can influence what happens there only by way of light or gravitational waves that travel at lightspeed.

In his book Spooky Action At A Distance, George Musser describes several non-quantum examples of non-locality.  In each case, there’s no signal transmission but somehow there’s a remote status change anyway.  We don’t (yet) know a good mechanism for making that happen.

It all suggests two speed limits, one for light and matter and the other for Einstein’s “deeper reality” beneath quantum mechanics.

~~ Rich Olcott

Smack-dab in the middle

On By rolcottIn Cosmology, General: Fun Stuff, Mathematics: Dimensions, UncategorizedLeave a comment

BridgeSee that little guy on the bridge, suspended halfway between all the way down and all the way up?  That’s us on the cosmic size scale.

I suspect there’s a lesson there on how to think about electrons and quantum mechanics.

Let’s start at the big end.  The physicists tell us that light travels at 300,000 km/s, and the astronomers tell us that the Universe is about 13.7 billion years old.  Allowing for leap years, the oldest photons must have taken about 4.3×1017 seconds to reach us, during which time they must have covered 1.3×1026 meters.  Double that to get the diameter of the visible Universe, 2.6×1026 meters.  The Universe probably is even bigger than that, but far as I can see that’s as far as we can see.

At the small end there’s the Planck length, which takes a little explaining.  Back in 1899, Max Planck published his epochal paper showing that light happens piecewise (we now call them photons).  In that paper, he combined several “universal constants” to derive a convenient (for him) universal unit of length: 1.6×10-35 meters.  It’s certainly an inconvenient number for day-to-day measurements (“Gracious, Junior, how you’ve grown!  You’re now 8×1034 Planck-lengths tall.”).  However, theoretical physicists have saved barrels of ink and hours of keyboarding by using Planck-lengths and other such “natural units” in their work instead of explicitly writing down all the constants.

Furthermore, there are theoretical reasons to believe that the smallest possible events in the Universe occur at the scale of Planck lengths.  For instance, some theories suggest that it’s impossible to measure the distance between two points that are closer than a Planck-length apart.  In a sense, then, the resolution limit of the Universe, the ultimate pixel size, is a Planck length.

sizelineSo that’s the size range of the Universe, from 1.6×10-35 up to 2.6×1026 meters. What’s a reasonable way to fix a half-way mark between them?

It makes no sense to just add the two numbers together and divide by two the way we’d do for an arithmetic average. That’d be like adding together the dime I owe my grandson and the US national debt — I could owe him 10¢ or $10, but either number just disappears into the trillions.

The best way is to take the geometrical average — multiply the two numbers and take the square root.  I did that.  It’s the X in the sizeline, at 6.5×10-5 meters, or about the diameter of a fairly large bacterium.  (In the diagram, VSC is the Vega Super Cluster, AG is the Andromeda Galaxy, and the numbers are those exponents of 10.)

That’s worth marveling at.  Sixty orders of magnitude between the size of the Universe and the size of the ultimate pixel.  Yet from blue whales to bacteria, Earth’s life just happens to occupy the half-dozen orders right in the middle of the range.  We think that’s it.

Could this be another case of the geocentric fallacy?  Humans were so certain that Earth was the center of the Universe, before Brahe and Galileo and Newton proved otherwise.  Is there life out there at scales much larger or much smaller than we imagine?

Who knows? But here’s an intriguing physics/quantum angle I’d like to promote.  We know a lot about structures bigger than us — solar systems and binary stars and galaxy clusters on up.  We know a few sizes and structures a bit smaller — viruses and molecules and atoms.  We’re aware of quarks and gluons that reside inside protons and atomic nuclei, but we don’t know their size or structure.

Even a proton is huge on the Planck-length scale.  At 1.8×10-15 meters the proton measures some 1020 Planck-lengths.  There’s as much scale-space between the Planck-length and the proton as there is between the Earth (1.3×107 meters) and the Universe.

It’s hard to believe that Terra infravita’s area has no structure whereas Terra supravita is so … busy.  The Standard Model’s “ultimate particles,” the electrons and photons and neutrinos and quarks and gluons, all operate down there somewhere.   It’s reasonable to suppose that they reflect a deeper architecture somewhere on the way down to the Planck-length foam.

Newton wrote (in Latin), “I do not make hypotheses.”  But golly, it’s tempting.

~~ Rich Olcott

There’s a lot of not much in Space

On By rolcottIn Cosmology, General: Fun Stuff, Mathematics: Dimensions, Uncategorized2 Comments

A while ago I drove from Denver to Fort Worth, and I was impressed. See, there’s a lot of not much in eastern Colorado. It’s pretty much the same in western Oklahoma except there’s less not much because there’s less of Oklahoma – but Texas has way more not much than anybody.

That gives Texas not much to brag about, but they do the best they can, bless their hearts.

What got me started on this rant was a a pair of astronomical factoids Katherine Kornei wrote in the Nov 2014 Discover magazine.

“If galaxies were shrunk to the size of apples, neighboring galaxies would be only a few meters apart….”
“If the stars within galaxies were shrunk to the size of oranges, they would be separated by 4,800 kilometers (3,000 miles).”

Apple orangeSo there’s a lot of not much between galaxies, but a whole lot more not much, relatively speaking, within them. I just measured an apple and an orange in my kitchen. They’re both about the same size, 3 inches in diameter, so I have no idea why she chose different fruits – perhaps she wanted to avoid comparing apples and oranges.

Anyway, if you felt like doing the galaxy visualization you could put two apple galaxies on the floor about 12 feet apart and then line up about 50 apples between them. A fair amount of space for more galaxies.

To see inside a galaxy you could put one orange star in Miami FL, and its on-the-average nearest orange neighbor in Seattle WA. Then you could set out a long skinny row of just about 63 million oranges in between. Oh, and on this scale the nearest galaxy would be about 2 billion miles (or 43 quadrillion oranges) away. Way more not much inside a galaxy than between two neighboring ones.

So if we squeeze all those apples and oranges together we’d get rid of all the empty space, right?

Not by a long shot. Nearly all those stars are balls of very hot gas, which means they’re made up of atoms crossing empty space inside the star to collide with other atoms. Relative to the size of the atoms, how much empty space is there inside the star?

Matryoshkii 1For example, every chemistry student learns that 6×1023 molecules of any gas take up a volume of 22.4 liters at normal Earth temperature and pressure. For a single-atom gas like helium that works out to about 22 atom-widths between atoms.

Now think about emptiness inside the Sun. If it’s a typical star (which it is) and if all of its atoms are hydrogen (which they mostly are) and if the average density of the Sun (1408 kg/m3) applied all the way down to the center of the Sun (which it doesn’t), and if we believe NASA’s numbers for the Sun (hey, why not?), then the average density works out to about 0.7 atom-widths between neighbors.

So no empty space to squeeze out of the Sun, eh? Well, actually there is quite a lot, because those atoms are mostly empty space, too.

OK, I cheated up there about the Sun, because virtually all of the Sun’s atoms have been dissociated into separated electrons and nuclei. The nucleus is much smaller than than its atom – by a factor of 60,000 or so. Think of a grape seed in the middle of a football field.

To sum it upward, we’ve got a set of Russian matryoshka dolls, one inside the next. At the center is a collection of grape seeds, billions and billions of them, each in their own football field. The football fields are all balled into a stellar orange (or maybe an apple), but there are billions of those crammed into a galactic apple (or maybe an orange) that’s about ten feet away from the nearest other piece of fruit.

As Douglas Adams wrote in Hitchhiker’s Guide to The Galaxy,

“Space … is big. Really big. You just won’t believe how vastly, hugely, mindbogglingly big it is. I mean, you may think it’s a long way down the road to the chemist’s, but that’s just peanuts to space…”

The thing to realize is that the function of all that space is to keep everything from being in the same place. That’s important.

~~ Rich Olcott

And now for some completely different dimensions

On By rolcottIn Mathematics: Dimensions, Physics: Fundamentals, UncategorizedLeave a comment

Terry Pratchett wrote that Knowledge = Power = Energy = Matter = Mass.  Physicists don’t agree because the units don’t match up.

Physicists check equations with a powerful technique called “Dimensional Analysis,” but it’s only theoretically related to the “travel in space and time” kinds of dimension we discussed earlier.

Place setting LMTIt all started with Newton’s mechanics, his study of how objects affect the motion of other objects.  His vocabulary list included words like force, momentum, velocity, acceleration, mass, …, all concepts that seem familiar to us but which Newton either originated or fundamentally re-defined. As time went on, other thinkers added more terms like power, energy and action.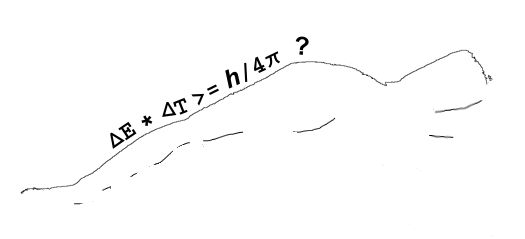

They’re all linked mathematically by various equations, but also by three fundamental dimensions: length (L), time (T) and mass (M). (There are a few others, like electric charge and temperature, that apply to problems outside of mechanics proper.)

Velocity, for example.  (Strictly speaking, velocity is speed in a particular direction but here we’re just concerned with its magnitude.)   You can measure it in miles per hour or millimeters per second or parsecs per millennium — in each case it’s length per time.  Velocity’s dimension expression is L/T no matter what units you use.

Momentum is the product of mass and velocity.  A 6,000-lb Escalade SUV doing 60 miles an hour has twice the momentum of a 3,000-lb compact car traveling at the same speed.  (Insurance companies are well aware of that fact and charge accordingly.)  In terms of dimensions, momentum is M*(L/T) = ML/T.

Acceleration is how rapidly velocity changes — a car clocked at “zero to 60 in 6 seconds” accelerated an average of 10 miles per hour per second.  Time’s in the denominator twice (who cares what the units are?), so the dimensional expression for acceleration is L/T2.

Physicists and chemists and engineers pay attention to these dimensional expressions because they have to match up across an equal sign.  Everyone knows Einstein’s equation, E = mc2. The c is the velocity of light.  As a velocity its dimension expression is L/T.  Therefore, the expression for energy must be M*(L/T)2 = ML2/T2.  See how easy?

Now things get more interesting.  Newton’s original Second Law calculated force on an object by how rapidly its momentum changed: (ML/T)/T.  Later on (possibly influenced by his feud with Leibniz about who invented calculus), he changed that to mass times acceleration M*(L/T2).  Conceptually they’re different but dimensionally they’re identical — both expressions for force work out to ML/T2.

Something seductively similar seems to apply to Heisenberg’s Area.  As we’ve seen, it’s the product of uncertainties in position (L) and momentum (ML/T) so the Area’s dimension expression works out to L*(ML/T) = ML2/T.

SeductiveThere is another way to get the same dimension expression but things aren’t not as nice there as they look at first glance.  Action is given by the amount of energy expended in a given time interval, times the length of that interval.  If you take the product of energy and time the dimensions work out as (ML2/T2)*T = ML2/T, just like Heisenberg’s Area.

It’s so tempting to think that energy and time negotiate precision like position and momentum do.  But they don’t.  In quantum mechanics, time is a driver, not a result.  If you tell me when an event happens (the t-coordinate), I can maybe calculate its energy and such.  But if you tell me the energy, I can’t give you a time when it’ll happen.  The situation reminds me of geologists trying to predict an earthquake.  They’ve got lots of statistics on tremor size distribution and can even give you average time between tremors of a certain size, but when will the next one hit?  Lord only knows.

File the detailed reasoning under “Arcane” — in technicalese, there are operators for position, momentum and energy but there’s no operator for time.  If you’re curious, John Baez’s paper has all the details.  Be warned, it contains equations!

Trust me — if you’ve spent a couple of days going through a long derivation, totting up the dimensions on either side of equations along the way is a great technique for reassuring yourself that you probably didn’t do something stupid back at hour 14.  Or maybe to detect that you did.

~~ Rich Olcott

Dimensional Venturing, Part 6 – Tiny Dimensions

On By rolcottIn Cosmology, Mathematics: Dimensions, Uncategorized1 Comment

“The Universe is much larger than is generally supposed.”  

What a great opening line, eh?  Decades later I still recall reading that in a technical paper about then-recent adjustments in the way astronomical distances were measured.

The authors didn’t know the half of it.  They were thinking in only three dimensions.  That’s so last-century.

If you read science articles in the popular press you’ve probably run into statements like this one from Brian Green’s article “Hanging by a String” in the January 2015 Smithsonian:

String theory’s equations require that the universe has extra dimensions beyond the three of everyday experience – left/right, back/forth and up/down…. [T]heorists realized that there might be two kinds of spatial dimensions: those that are large and extended, which we directly experience, and others that are tiny and tightly wound, too small for even our most refined equipment to reveal.

Tightly wound dimensions?  What’s that about?  And what’s it got to do with strings?

The “large extended” dimensions are the kind we discussed in Part 1 of this series.  The essential point is that (in principle) once you or a light ray start moving in a particular direction you can keep going in that direction forever.

Seems obvious, how else could it be?

tiny dimension 1Well, suppose that we bend one of those three familiar “large” dimensions around in a circle, as in the drawing to the right. Our little guy could walk straight out of the page “forever” in the X direction. He could walk straight up the page “forever” in the Z direction. However, if he tries to walk along the Y track perpendicular to both of those two, in a while he’ll wind up right back where he started.

That’s an example of a “tightly wound” dimension.

Because it makes the math easier, physicists usually don’t calculate the absolute distance traveled around the circle.  Instead they write equations that depend on the angle from zero as the starting point. Notice that 360 degrees is exactly the same as zero — that’ll be important in a later post here.  Anyhow, there’s reason to believe that the effective circumference of a “tightly wound” dimension is really, really small.

OK, having a closed-off dimension is a little strange but it’s just not real-world, is it?

tiny dimension 2Actually, our real world is like that but moreso. Look at this drawing where we’ve got a pair of perpendicular wound-up dimensions. The little guy on the Y track can go from Denver down to Mazatlan in Mexico and proceed all the way around the world back up to Denver. On the X track he’s going from Denver westward to Chico CA and could continue across the Pacific and onward until he gets back to Denver The only way he can travel in one direction “forever” is to go along the Z track, straight upward, and that’s why NASA builds rocket ships.

Back to the strings. Depending on which variety of string theory you choose, the strings wriggle in a space of three Z-style “extended” dimensions, plus time, plus half-a-dozen or more wound-up or “compactified” (look it up) dimensions.  If string-theory strings can wriggle in all those directions, then how much room does each one have to move around in?  We’ve all learned the formulas for area of a rectangle and volume of a cube — [length times height] and [length times height times depth].  To extend the notion of “volume” to more dimensions you just keep multiplying.

Back to the size of the Universe. You may think that just with straight-line space it’s pretty good-sized.  With those stringy dimensions in play, for every single cube-shaped region you pick in straight-line space you need to multiply that volume by [half-a-dozen or more dimensions] times [many possible angles] to account for all the “space” in all the enhanced regions you could choose from when you include those wound-up dimensions. The total multi-dimensional volume is very, very huge.

The universe is indeed much larger than is generally supposed.

Next week — buttered cats.

~~ Rich Olcott

Dimensional Venturing Part 5 – You Ain’t From Around Here, Are You?

On By rolcottIn Cosmology, Mathematics: Dimensions, UncategorizedLeave a comment

OK, I’ll admit it, back in the day I read a lot of comics.  Even then, though, I was skeptical — “Wait, how could Superman just pick up that building?  It’d fall apart!”

But I was intrigued by one recurring character, Mr Mxyzptlk, a pixie-like “visitor from the 5th dimension.”   His primary purpose in life (other than getting us to buy more comics) seemed to be to play tricks on or otherwise torment Our Hero.

Mxycus 2Mxy wasn’t the only comics character coming in “from another dimension.” It seemed like the entire Marvel team (both sides) was continually flickering out of and into our universe that way. How often did Jane Grey die and then somehow get cloned or refreshed?  (BTW, if the accompanying cartoon is a little obscure, show it to the friendly clerks at your local comics store — it may give them a chuckle.)

But my question was, where was that dimension Mxy came from?  I got an answer, sort of, when our geometry teacher explained that a dimension is just a direction you could travel.  Different dimensions are directions at right angles to each other.  She was right (see my first post in this series), at least in the context of then-HS math, but that explanation opened an editorial issue that’s never been properly settled.

A dimension is a direction, not a location.  You can’t be “from” a fifth or sixth or nth dimension any more than you can be from up.  If there is a spatial fifth dimension, we’re already “in” it in the same sense that we’re already somewhere along east-to-west and somewhen along past-to-future.

What’s going on is that for the purpose of the story, the authors want the character to come from somewhere very else.  We often associate a place with the direction to it — the sun rises in the east, Frodo departs to the west,  Heaven is up, Hell is down — but those are all directions relative to our current location.  We even associate future times as being in front of us and past times behind us (there’s that 4th dimension again).

Mash_sign_post
The M*A*S*H signpost, now at the Smithsonian. Photo by Steven Williamson., in commons.wikimedia.org/wiki/File:Mash_sign.jpg

But a place is more specific than a direction — to navigate to a certain there you need to know the direction and the distance (or another quantity that stands in for a distance).  That matters.  Jimmie Rodgers sang, “Twelve more miles to Tucumcari” as he kept track of the distance left to go along the road he was traveling.  Or away from the town, as it turned out.

Physicists have lots of uses for the combination of a direction and a magnitude, so many that they gave the combination a name — a vector.  The vector may represent a direction and a distance, a direction and the strength of a magnetic field, or a direction and any quantity that happens to be useful in the application at hand.  A wind map uses vectors of direction and wind speed to show air flow.  Here’s a very nice wind map of the US, and I love NOAA’s wind map of the world.  Vectors will be real useful when we start talking about black holes.

OK, so Mr Mxyzpltk (the spelling seemed to vary from issue to issue of the comic) comes from somewhere along a fifth dimension, but they never tell us from how far away.

Next week –As Steve Martin said, “Let’s get small, really small.”

~~ Rich Olcott

Dimensional Venturing Part 4 – To infini-D and beyond!

On By rolcottIn Cosmology, Mathematics: Dimensions, UncategorizedLeave a comment

apple plumNow that you’ve read my previous posts and have the 4-D thing working well, you’re ready to go for a few more dimensions.  Consider the apple that struck Isaac Newton’s head.  The event occurred in 1665, in England at 52°55´N by 0°38´E, roughly three feet above ground level.  The apple, variety “Flower of Kent,” weighed about 8 ounces and was probably somewhat past fully ripened.  Got that picture in your head?  You’re doing great.

Now visualize the apple taking thirty seconds to move twenty feet diagonally upward, northward and eastward as it morphs to an underripe 4-ounce Damson plum.

The change you just imagined followed an eight-dimensional path: three dimensions of space, one of time, one of weight, one for degree of ripeness, and two category dimensions, species and variety.

Length in a given direction is only one kind of dimension, as Sir Isaac’s example demonstrates.  A mathematician would say that a dimension is a set of values that can be traversed independently of any other set of values. A dimension can be confined to a limited range (360 degrees in a circle) or be infinite like … well, “infinitely far away.”  A dimension might be continuous (think how loudness can vary smoothly from sleeping-baby hush to stadium ROAR and beyond) or be in discrete steps like the click-stops on a digital controller.  The physicists are arguing now whether, at the smallest of scales, space itself is continuous or discrete.

colors_post
Photo by Becky Ziemer

Color vision’s a good example of dimensions in action.  For most of us, our eyes have three types of cone cells, respectively optimized for red, green and blue light.  We see a specific color as some mixture of the three and that’s how the screen you’re looking at now can fake 16 million colors using just three kinds of color-emitting elements (phosphor dots in old-style TVs, LEDs in most devices these days).

Where did that 16 million number come from?  The signal-processing math is seriously techie, but at the bottom the technology uses 256 intensity levels of red, 256 levels of green and 256 levels of blue — each is a discrete dimension with a limited range.  Together they define a 256x256x256-point cube.  Any point in that cube represents a unique mix of primary colors.  One of the colors in the little girl’s hat, for instance, is at the intersection of 249/256 red, 71/256 green, and 48/256 blue.  The arithmetic tells us there are 16,777,216 points (possible mixed colors) in that cube.

Well, actually, there’s one more dimension to color vision because our eyes also have rod cells that simply sense light or darkness.  Neither brown nor grey are in the spectrum that cones care about.  A good printer uses four separate inks to produce browns and greys as mixtures of three dimensions of red-green-blue plus one of black.

So color is 3-dimensional, mostly.  But that’s just the start of color vision because most of us have millions of cone cells in each eye.  A mathematician would say that any scene you look at has that number of dimensions, because the intensity registered by one cone can vary in its range independently of all the other cones.

Ain’t it wonderful that you’re perfectly OK with living in a multi-million-dimensional world?

Next week – a word from the other side

~~ Rich Olcott