Category: Mathematics: Spherical Harmonics

A Spherical Bandstand

On By rolcottIn Astronomy: Planetary Science, Mathematics, Mathematics: Spherical Harmonics, UncategorizedLeave a comment
Radial harmonics Rn = Ln e-nr

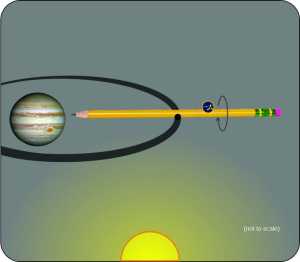
“Whoa, Sy, something’s not right. Your zonal harmonics — I can see how latitudes go from pole to pole and that’s all there are. Your sectorial harmonic longitudes start over when they get to 360°, fine. But this chart you showed us says that the radius basically disappears crazy close to zero. The radius should keep going forever, just like x, y and z do.”

“Ah, I see the confusion, Susan. The coordinate system and the harmonic systems and the waves are three different things, um, groups of things. You can think of a coordinate system as a multilevel stage where chords of harmonic musicians can interact to play a composition of wave signals. The spherical system has latitude and longitude levels for the brass and woodwind players, plus one in back for the linear percussion section. Whichever direction the brass and woodwinds point, that’s where the signals go out, but it’s the percussion that determines how far they get. Sure, radius lines extend to infinity but except for R0 radial harmonics damp out pretty quickly.”

“Signals… Like Kaski’s team interpreted Juno‘s orbital twitches as a signal about Jupiter’s gravitational unevenness. Good thing Juno got close enough to be inside the active range for those radial harmonics. How’d they figure that?”

“They probably didn’t, Cathleen, because radial harmonics don’t fit easily into real situations. First problem is scale — what units do you measure r in? There’s an easy answer if the system you’re working with is a solid ball, not so easy if it’s blurry like a protein blob or galaxy cluster.”

“What makes a ball easy?”

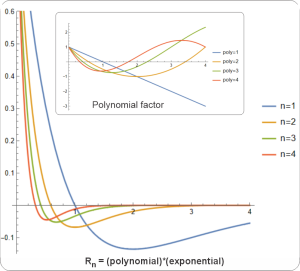
“Its rigid surface that doesn’t move so it’s always a node. Useful radial harmonics must have a node there, another node at zero and an integer number of nodes between. Better yet, with the ball’s radius as a natural length unit the r coordinate runs linearly between zero at the center and 1.0 at the surface. Simplifies computation and analysis. In contrast, blurries usually don’t have convenient natural radial units so we scrabble around for derived metrics like optical depth or mixing length. If we’re forced into doing that, though, we probably have worse challenges.”

“Like what?”

“Most real-world spherical systems aren’t the same all the way through. Jupiter, for instance, has separate layers of stratosphere, troposphere, several chemically distinct cloud‑phases, down to helium raining on layers of hydrogen in liquid, maybe slushy or even solid form. Each layer has its own suite of physical properties that put kinks into a radial harmonic’s smooth curve. Same problem with the Sun.”

“How about my atoms? The whole Periodic Table is based on atoms having a shell structure. What about the energy level diagrams for atomic spectra? They show shells.”

“Well, they do and they don’t, Susan. Around the turn of the last Century, Lyman, Balmer, Paschen, Brackett and Pfund—”

“Sounds like a law firm.”

“<ironically> Ha, ha. No, they were experimental physicists who gave the theoreticians an important puzzle. Over a 40‑year period first Balmer and then the others, one series at a time, measured the wavelengths of dozens of lines in hydrogen’s spectrum. ’Okay, smarties, explain those!‘ So the theoreticians invented quantum mechanics. The first shot did a pretty good job for hydrogen. It explained the lines as transitions between discrete states with different energy levels. It then explained the energy levels in terms of charge being concentrated at different distances from the nucleus. That’s where the shell idea came from. Unfortunately, the theory ran into problems for atoms with more than one electron.”

“Give us a second… Ah, I get why. If one electron avoids a node, another one dives in there and that radius isn’t a node any more.”

“Got it in one, Cathleen. Although I prefer to think of electrons as charge clouds rather than particles. Anyhow, when an atom has multiple charge concentrations their behavior is correlated. That opens the door to a flood of transitions between states that simply aren’t options for a single‑electron system. That’s why the visible spectrum of helium, with just one additional electron, has three times more lines than hydrogen does.”

“So do we walk away from spherical harmonics for atoms?”

“Oh, no, Susan, your familiar latitude and longitude harmonics fit well into the quantum framework. These days, though, we mostly use combinations of radial fade‑aways like my Sn00 example.”

~~ Rich Olcott

Jupiter And The Atoms

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

“Okay, Sy, what’s your third solution?”

“Solution to what, Susan?”

“These harmonic thingies. They’re about angles so it makes sense to chart them in polar or spherical coordinates, but when they take on negative values the radius goes the wrong way. You said one solution was to chart the negatives in a different color. That’s confusing, though. Another solution is to square all the values to get everything into positive territory. That’s okay for chemists like me because the peaks and nodes we care about stay in the same places. What’s the third option?”

“One that gets to why these ‘harmonic thingies’ are interesting at all. When Juno‘s orbiting Jupiter, does it feel each of Kaspi’s Jn shapes individually?”

“No, of course not, she just reacts to how they all add togethherrr … Oh! So you’re saying we can handle negative values from one harmonic by adding it to another one that’s more positive and plotting the combination.”

<pointing to paper napkin> “Bingo! Remember this linear plot of J2 where I colored its negative section pink?” <pointing to display on Old Reliable> “When you multiply J2 by C0 you get S220. I added that to four helpings of Sn00 to get this combination.”

“Ah, that negative region in S220‘s middle shaves back the equator on Sn00‘s sphere while the positive part adds bumps top and bottom.” <Susan gives me the side‑eye> “Why’d you pick that 4‑to‑1 ratio, and what’s with those n subscripts instead of numbers?”

“Getting a little ahead of myself. For the moment let’s concentrate on Juno‘s experience with Jupiter’s gravity. One reason I chose that ratio was that it’s pretty easy to see in the picture. In real cases the physical system determines the ratios. Kaspi’s team derived their ratios experimentally. They used math to fit a model to Juno‘s very slightly wobbly orbit. Their model of Jupiter’s gravity field started from the spherical J0 shape. They tweaked that by adding different ratios of J2 through J40, adjusting the ratios until the model’s total gravity field predicted an orbit that matched the real‑world one. J2‘s share was about 15 parts per thousand but most of the rest contributed less than a part per million. Jupiter probably uses multiple mass blobs to make the J2 shape. The point is, the planet’s really a mess but we can analyze the mess in terms of the harmonics.”

“So that’s how you drew what Cal called your wiggle-waggles — you followed Kaski’s Jn recipe and then added some constant to push the polar plot out far enough that the negatives didn’t poke out the wrong side. That constant — what value did you use and why that one?”

“That’s exactly what I did do, Cathleen. Frankly, I don’t even remember what constant I added, just something that was big enough to make the negatives behave nicely, not so large that the peaks vanished by comparison. Calibrating accurately to Jupiter’s J0 would shrink the peaks down to parts‑per‑thousand invisibility. After all, I was more concerned with peak position than peak size.”

“Now we’re back to your 4‑to‑1 ratio. Was that arbitrary, too?”

“No, it wasn’t, Susan. Would it have been closer to Chemistry if I’d labeled that figure as 1s22s22p1?”

“Two electrons in the 1s‑shell, two in the 2s‑shell plus one 2p electron … that’s a boron atom? But you’re showing only one radial shell, not two separate ones.”

“True, but that’s to make another point. There isn’t an electron in the 1s shell, or even a pair of them nicely staying on opposite sides. The atom’s charge, all five electrons‑worth of it, is smeared out as a wave pattern across the entire structure. The Sn00 pattern captures everything that’s spherical. The S220 pattern gets what’s left.”

“But what about the radial nodes? Isn’t that the difference between 1s and 2s, that 2s has a node?”

“Oh there are nodes, alright, but they don’t have much effect. Each radial harmonic is the product of two factors — a polynomial and an exponential. The exponential part squeezes the polynomial so hard that adjacent peaks and valleys are barely bumps and dents.”

“So Jupiter and atoms use the same math, huh?”

“So does the Sun.”

~~ Rich Olcott

Shapes And Numbers

On By rolcottIn Mathematics: Spherical Harmonics, Physics: Quantum Mechanics, UncategorizedLeave a comment

I’m nursing my usual mug of eye‑opener in Cal’s Coffee Shop when astronomer Cathleen and chemist Susan chatter in and head for my table. Susan fires the first volley.

“Sy, those spherical harmonics you’ve posted don’t look anything like the atomic orbitals in my Chem text. Shouldn’t they?”
 ”How do you add and multiply shapes together?”
  ”What does the result even mean?”
   ”And what was that about solar seismology?”

The angular portion of the lowest‑energy spherical harmonics.
Adapted from work by Inigo.quilez, under CCA SA 3.0 license

“Whoa, have you guys taken interrogation lessons from Mr Feder? One at a time, please. Let’s start with the basics.” <sketching on a paper napkin> “For example, the J2 zonal harmonic depends only on the latitude, not on the longitude or the distance from the center, so whatever it does encircles the axis. Starting at the north pole and swinging down to the south pole, the blue line shows how J2 varies from 1.0 down to some negative decimal. At any latitude, whatever else is going on will be multiplied by the local value of J2.”

“The maximum is 1.0, huh? Something multiplied by a number less than 1 becomes even smaller. But what happens where J2 is zero? Or goes negative?”

“Wherever Jn‘s zero you’re multiplying by zero which makes that location a node. Furthermore, the zero extends along its latitude all around the sphere so the node’s a ring. J2‘s negative value range does just what you’d expect it to — multiply by the magnitude but flip the product’s sign. No real problem with that, but can you see the problem in drawing a polar graph of it?”

“Sure. The radius in a polar graph starts from zero at the center. A negative radius wouldn’t make sense mixed in with positives in the opposite direction.”

“Well it can, Cathleen, but you need to label it properly, make the negative region a different color or something. There are other ways to handle the problem. The most common is to square everything.” <another paper napkin> “That makes all the values positive.”

“But squaring a magnitude less than 1 makes it an even smaller multiplier.”

“That does distort the shapes a bit but it has absolutely no effect on where the nodes are. ’Nothin’ times nothin’ is nothin’,’ like the song says. Many of the Chem text orbital illustrations I’ve seen emphasize the peaks and nodes. That’s exactly what you’d get from a square‑everything approach. Makes sense in a quantum context, because the squared functions model electron charge distributions.”

“Thanks for the nod, Sy. We chemists care about charge peaks and nodes around atoms because they control molecular structures. Chemical bonds and reactions tend to localize near those places.”

“I aim for fairness, Susan. There is another way to handle a negative radius but it needs more context to look reasonable. Meanwhile, we’ve established that at any given latitude each Jn is just a number so let’s look at longitudes.” <a third paper napkin> “Here’s the first two sectorial harmonics plotted out in linear coordinates.”

“Looks familiar.”

“Mm‑hm. Similar principles, except that we’re looking at a full circle and the value at 360° must match the value at 0°. That’s why Cm always has an even node count — with an odd number you’d have -1 facing +1 and that’s not stable. In polar coordinates,” <the fourth paper napkin> “it’s like you’re looking down at the north pole. C0 says ‘no directional dependence,’ but C1 plays favorites. By the way, see how C1‘s negative radii in the 90°‑270° range flip direction to cover up the positives?”

“Ah, I see where you’re going, Sy. Each of these harmonics has a numeric value at each angle around the center. You’re going to tell us that we can multiply the shapes by multiplying their values point by point, one for each latitude for a J and each longitude for a C.”

“You’re way ahead of me as usual, Cathleen. You with us, Susan?”

“Oh, yes. In my head I multiplied your J2 by C0 and got a pz orbital.”

“I’m impressed.”
 ”Me, too.”

“Oh, I didn’t do it numerically. I just followed the nodes. J2 has two latitude nodes, C0 has no longitude nodes. There it is, easy‑peasy.”

~~ Rich Olcott

A Loose-end Lagniappe

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“We have some loose ends to tie up. Too early for pizza. Coffee at Cal’s?”

“Hello, ‘Walt‘. Fifteen minutes?”

“Confirmed.”

He’s at a back table, facing the door, of course. He points to the steaming mug and strawberry scone beside it on the table. I nod to acknowledge. ”So, Walt, what are these loose ends?”

“My people say that Juno‘s not on a 53‑day orbit any more. NASA’s jiggled it down to 33 days. What’s that do to the numbers you gave me?”

<sliding a folded paper scrap across the table> “I had a hunch you’d want more so I worked up estimates. Juno started with a 53‑day orbit but a Ganymede flyby dropped it to 43 days. A Europa flyby took Juno to a 38‑day orbit. Now it’s swerved by Io and we’re at 33 days. I threw in the 23‑day line for grins, no extra charge.”

“Half the orbit size but no significant change in the close‑in specs. That’s surprising.”

“Not really. It’s like a dog’s butt wagging its tail. At close approach, we call it perijove, Juno is only 76 500 kilometers out from Jupiter’s center. Its orbit thereabouts is pretty much nailed down by the big guy’s central field. But there’s no second attractor to constrain the orbit’s other extreme millions of kilometers out. Do an Oberth burn near perijove or arrange for a gravity tweak from a convenient moon, you get a big difference at the far end.”

“That wraps that.” <reaches for his cane, then settles back to do a Columbo> “Just one more thing, Moire. I came in with a question about the Sun’s effect on Juno. You took care of that pretty quick but spent a load of my time and consultancy budget on these spherical harmonics. How come?”

“As I recall, you and your people kept coming back for more detail. Also, the 225 000‑kilometer radius I got from R2‘s structure was essential in calculating these close‑in numbers. You’re getting your money’s worth. I’ll even throw in a lagniappe.”

“A free gift? I never trust them.”

“Such a mean world you live in, Walt.” <displaying an image on Old Reliable> “Here it is, take it or leave it.”

Top: F000 plus a time-varying contribution from F660
Bottom: C0 plus a time-varying contribution from C4

“What is it?”

“It’s a bridge between the physics of light and sound, and the physics of atoms and stars. When I say ‘coordinates,’ what words spring to your mind?”

“Traverse and elevation.”

“Interesting choice. Any other systems?”

“Mm, latitude, longitude and altitude. And x‑y‑z if you’re in a classroom.”

“Way beyond the classroom. You use spreadsheets, right?”

“Doesn’t everyone?”

“Rows‑columns‑sheets is x‑y‑z. On digital screens, pixels‑lines‑luminosity is x‑y‑z. Descarte’s rectilinear invention is so deeply embedded in our thinking we don’t even notice it. Perpendicular straight‑line coordinates fit things that are flat or nearly so, not so good for spheres and central‑force problems. Movement there is mostly about rotation, which is why your first two picks were angular instead of linear.”

“Okay, but our choice of coordinates is our choice. What have x‑y‑z or your Fnnm to do with natural things?”

“Overtones and resonance. Look at that black line in the movie. It could be a guitar string or a violin string, doesn’t matter. One end’s fixed to the instrument’s bridge, the other end’s under somebody’s finger. All other points on the string are free to move, subject to tension along the string. Then someone adds energy to the string by plucking or bowing it.”

“At one of those peaks or valleys, right?”

“Nope, anywhere, which goes to my point. The energy potentially could contort the string to any shape. Doesn’t happen. The only stable shapes are combinations of sine waves with an integer number of nodes, like C4‘s quartet. Adding even more energy gives you overtones, waves that add in‑between nodes to lower‑energy waves. C0‘s no‑nodes black line could run along x, y or z in any flat system.”

“So you’re going to tell me that your C‘s, J‘s and R‘s support wave structures for spheres.”

“Indeed. All four giant planets have stripes along their J arcs. Solar seismologists have uncovered C, R and maybe J wave structures inside the Sun.”

“Bye.”

“Don’t mention it.”

~ Rich Olcott

Completing The Triad

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

Walt’s mustache bristles as he gives me the eye. ”You claim three harmonics control how the Sun’s gravity could affect spacecraft orbits around a target planet like Jupiter. You said we don’t have to care about Jupiter’s gravitational zones and isolating the sectors probably isn’t doable. What’s the third?”

Time to twist the screws. ”Three harmonic systems, Walt, all working together and you’ve got their names wrong. They control nothing, they’re a framework for analysis. And Jupiter’s special. Solar gravity doesn’t affect its zonal harmonic arcs but that’s only because Jupiter’s polar axis is nearly perpendicular to its orbital plane. Zonal‑effect N‑S twisting at Jupiter is pennies on a C‑note. Any mission we send to Mars, Saturn or Uranus we’ll care a lot about their zonal harmonics because their axes have more tilt. An 82° tilt for Uranus, can’t get much more tilted than that. Sectorial harmonics may still help us navigate there because Uranus probably has a lot less magnetism than Jupiter.”

That rocks him but he comes back strong. ”The third kind of harmonic?!! C’mon, give!”

“Radial, the center‑out dimension. The gravitational force between bodies depends on center‑to‑center distances so yeah, your people would be interested.”

“I presume radial harmonics have numbers like Jn and Cm do?”

“They do. Sorry, this’ll get technical again but I’ll go as light as I can. Each radial harmonic is the product of two factors. You know about factors, right?”

“Sure, force multipliers.”

“You would know that kind. More generally, factors are things that get multiplied together. I’ll call the general radial harmonic Rn. It’s the product of two factors. The first is a sum of terms that begin with rn, where r is the distance. For instance, R3‘s first factor would look like a*r³+b*r²+c*r+d, where the a,b,c,d are just some numbers. Different radial harmonics have different exponents in their lead terms. You still with me?”

“Polynomials from high school algebra. Tell me something new.”

“The second factor decreases exponentially with n*r. No matter how large rn gets, when you multiply an rn polynomial by something that decreases exponentially, the (polynomial)×(exponential) product eventually gets really small.”

“Give me a second. … So what you’re saying is, at a big enough distance these radial harmonics just die away.”

“That’s where I was going.”

“How far is ‘enough’?”

“Depends on n. Higher values of n shut down faster.”

“So these Cms and Jns and Rns just add together?” <pauses, squints at me suspiciously> “Is there some reason you used n for both Jn and Rn?”

“No but yes, and yes. You combine a C, a J and an R using multiplication to get a full harmonic F, except there are rules. The J and R must belong to the same n. The m can’t be larger than n. From far away we’d model Jupiter’s gravity as F000=R0×J0×C0, which is an infinite sphere — R0 never dies away and J0×C0 says ‘no angular dependence.’ The Sun’s gravity acts along R0 and that’s what keeps Jupiter in orbit. If the problem demands combining full harmonics, you use addition.” <rousing a display on Old Reliable> “Here’s how a particular pair of harmonics combine to increase or decrease spherical gravity in specific directions.”

“But Juno doesn’t see those gravity lumps until it gets close‑in. How close?”

“R2‘s down to less than a part per thousand at three planetary radii, call it 225 000 kilometers away from the planet’s center.”

“How much time is it closer than that distance?”

“Complicated question. A precise answer requires some calculus — is your smart phone set up for elliptic integrals?”

“Of course not. A good estimate will do.”

“Okay, here’s the plan. What we’d like is total time spent while Juno travels along the ellipsoidal arc between points A and D where the orbit crosses the 225 000‑km circle. Unfortunately, Juno speeds up approaching point P, slows down going away — calculating the A‑D time is tricky. I’ll assume Juno travels straight lines AB and CD at the A-speed. I’ll also approximate the orbit’s close pass as a semicircle at P‑speed.” <tapping> “I get a 3.6-hour duration, less than 0.3% of the full 53-day orbit. Will that satisfy your people?”

“You’ll know if it doesn’t.”

~~ Rich Olcott

Sectorial Setbacks

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“Moire, you were holding out on me. Eddie’s, fifteen minutes.”

“Not so fast, Walt. That wasn’t me holding out, that was you leaving too soon. From now on you’re paying quite a bit more. And it’ll be thirty minutes.”

“So we’re negotiating, hmm?”

“That’s about the size of it. You still interested?”

“My people are, they sent me back here. Oh well. Thirty minutes.”

Thirty-three minutes later I walk into Eddie’s. Walt’s already gotten a table. He beckons, points to the freshly‑served pizza, raises an eyebrow.

“Apology accepted. What made your people unhappy?”

“You told me flat‑out that the Sun’s gravity couldn’t affect those zonal harmonics. Do you have anything to back that up?”

“Symmetry. Zonal harmonics and latitude are about north‑south. Each Jn is a pole‑to‑pole variation pattern. The only way solar gravity can tilt Jupiter’s north‑south axis is to exert torque along the zonal harmonics. Jupiter’s equator is within 3° of edge‑on to the Sun.” <showing an image on Old Reliable’s screen> “Here’s what the Sun sees looking at J10, for instance. Solar pull on any northern zone segment, say, would be counteracted by an equal pull on the corresponding southern segment of the same zone. No net torque, no tilt. J0‘s the only exception. It’s simply a sphere that doesn’t vary across the whole planet. The Sun’s pull along J0‘s arc can’t tilt Jupiter.”

“Okay, so the zonal picture’s too simple. Just one set of waves, running up and down the planet—”

“No, not running. One way to characterize a wave is by how its components change with time. You’re thinking like ocean waves that move from place to place as time goes by. There’s also standing waves like on a guitar string, where individual points move but the peaks and valleys don’t. There’s time‑only waves like how the day length here changes through the year. And there’s static waves where time’s not even in the equation. Jupiter’s stripes don’t move, they’re peaks and valleys in a static wave pattern. By definition, the zonal harmonic system is static like that. But you’re right, it’s only part of the picture.”

“Give me the part the Sun’s gravitational field does play with.”

“That’d be two parts — sectorial and radial harmonics. Sectorial is zonal’s perpendicular twin. Zonal wave patterns show variation along the polar axis; sectorial wave patterns Cm vary around it. I’m keeping it non‑technical for you but Cm‘s actually cos(m*x) where x is the longitude.”

“Just don’t let it go any farther.”

“I’ll try not to. My point is that each sector pattern can be labeled with a positive integer just like we did with the zones.”

“If the Jn arcs aren’t affected by solar gravity, why would I care about these Cms?”

“You wouldn’t, except for the fact that mass distribution across Jupiter’s sectors is probably lumpy. We know the Great Red Spot holds its position in the southern hemisphere and the planet’s magnetic field points way off to the side. Maybe those features mark off‑center mass deficits and concentrations. Suppose a particular sectorial wave’s peak sits directly over a mass lump or hole. Everything under that harmonic’s influence is tugged back and forth by solar gravity each time the wave traverses the day side. Juno in its N‑S path just isn’t an efficient sensor for those tugs. Good sectorial sensing would require an orbiter on an E‑W path, preferably right over the equator.  Any orbital wobbles we’d see could be fed into a sectorial gravity map. Cross that with the zonal map and we’d be able to locate underlying mass variations by latitude and longitude.”

“Not a good idea. Gravity’s not the only field in play. You’ve just mentioned Jupiter’s magnetic field. I’ve read it’s stronger than any other planet’s. If your E‑W orbiter’s built with even a small amount of iron, you’d have a hard time deciding which field was responsible for any observed irregularities.”

“Good point. The idea’s even worse than you think, though. Jupiter’s sulfur‑coated moon—”

“Io. Yes, your induction‑heating idea might even be real. What about it?”

“I haven’t written yet about the high‑voltage Io‑to‑Jupiter bridge made of sulfur, oxygen and hydrogen ions. Jupiter’s magnetism plays a complicated game with them but the result is a chaotic sheet of radiating plasma around the planet’s equator. An E‑W orbiter in there would be tossed about like a paper boat on the ocean.”

~~ Rich Olcott

A Pencil In Space

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, Physics: Newton and Gravity, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“I have a question I think you’ll find interesting, but it’s best we talk in person. Care for pizza?”

“If you’re buying.”

“Of course. Meet me at Eddie’s, twenty minutes. Bring Old Reliable.”

“Of course.”

Tall fellow, trimmed chevron mustache, erect bearing except when he’s leaning on that cane. “Moire?”

“That’s me. Good to meet you, Mr … ?”

“No names. Call me … Walt.”

We order, find a table away from the kitchen. “So, Walt, what’s this interesting question?”

“Been following this year’s Jupiter series in your blog. Read over the Kaspi paper, too, though most of that was over my head. What I did get was that his conclusions and your conclusions all come from measuring very small orbit shifts which arise from millionths of a g of force. Thing is, I don’t see where any of you take account of the Sun’s gravity. If the Sun’s pull holds Jupiter in orbit, it ought to swamp those micro-g effects. Apparently it doesn’t. Why not?”

“Well. That’s one of those simple questions that entail a complicated answer.”

“I’ve got time.”

“I’ll start with a pedantic quibble but it’ll clarify matters later on. You refer to g as force but it’s really acceleration. The one‑g acceleration at Earth’s surface means velocity changes by 980 meters/second per second of free fall. Drop a one kilogram mass, it’ll accelerate that fast. Drop a 100 kilogram mass, it’ll experience exactly the same acceleration, follow?”

“But the second mass feels 100 times the force.”

“True, but we can’t measure forces, only movement changes. Goes all the way back to Newton defining mass in terms of force and vice‑versa. Anyway, when you’re talking micro‑g orbit glitches you’re talking tiny changes in acceleration. Next step — we need the strength of the Sun’s gravitational field in Jupiter’s neighborhood.”

“Depends on the Sun’s mass and Jupiter’s mass. No, wait, just the Sun’s mass because that’s how it curves spacetime. The force depends on both masses.”

I’m impressed. “And the square of the very large distance between them.” <tapping on Old Reliable’s screen> “Says here the Sun’s field strength out there is 224 nano‑g, which is pretty small.”

“How’s that compare to what else is acting on Juno?”

<more tapping> “Jupiter’s local field strength crushes the Sun’s. At Juno’s farthest point it’s 197 micro‑g but at Juno’s closest point the field’s 22.7 million micro‑g and the craft’s doing 41 km/s during a 30-minute pass. Yeah, the Sun’s field would make small adjustments to Juno’s orbital speed, depending on where everybody is, but it’d be a very slow fluctuation and not the rapid shakes NASA measured.”

“How about side‑to‑side?”

“Good point, but now we’re getting to the structure of Juno’s orbit. Its eccentricity is 98%, a long way from circular. Picture a skinny oval pencil 8 million kilometers long, always pointed at Jupiter while going around it. It’s a polar orbit, rises above Jupiter on the approach, then falls below going away. The Sun’s effect is greatest when the orbit’s at right angles to the Sun‑Jupiter line. The solar field twists the oval away from N‑S on approach, trues it back up on retreat. That changes the angle at which Juno crosses Jupiter’s gravitational wobbles but won’t affect how it experiences the zonal harmonics.”

“Tell me about those zonal things.”

“A zone is a region, like the stripes on Jupiter, that circles a sphere at constant latitude. Technically, zonal harmonic Jn is the nth Legendre polynomial in cos(θ)—”

“Too technical.”

“Gotcha. Okay, each Jn names a shape, a set of gravitational ripples perpendicular to the polar axis. J0‘s a sphere with no ripples. Jupiter’s average field looks like that. A bigger n number means more ripples. Kaspi’s values estimate how much each Jn‘s intensity adds to or subtracts from J0‘s strength at each latitude. The Sun’s field can modify the intensity of J0 but none of the others.”

Walt grabs his cane, stands, drops a C‑note on the table. “This’ll cover the pizza and your time. Forget we had this conversation.” And he’s gone.

“Don’t mention it.”

~~ Rich Olcott

  • Thanks to Will, who asked the question.

Screaming Out Of Space

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

Cal (formerly known as Al) comes over to our table in his coffee shop. “Lessee if I got this right. Cathleen is smug twice. First time because the new results from Juno‘s data say her hunch is right that Jupiter’s atmosphere moves like cylinders inside each other. Nearly cylinders, anyhow. Second smug because Sy used the Juno data to draw a math picture he says shows the Great Red Spot but I’m lookin’ at it and I don’t see how your wiggle‑waggles show a Spot. That’s a weird map, so why’re you smug about it, Cathleen?”

“The map’s weird because it’s abstract and way different from the maps you’re used to. It’s also weird because of how the data was collected. Sy, you tell him about the arcs.”

“Okay. Umm… Cal, the maps you’re familiar with are two‑dimensional. City maps show you north‑south and east‑west, that’s one dimension for each direction pair. Maps for bigger‑scale territories use latitude for north‑south and longitude for east‑west but the principle’s the same. The Kaspi group’s calculations from Juno‘s orbit data give us a recipe for only a one‑dimensional map. They show how Jupiter’s gravity varies by latitude, nothing about longitude. We could plot that as a rectangle, latitude along the x‑axis, relative strength along the y‑axis. I thought I’d learn more by wrapping the x‑axis around the planet so we could look for correlations with Jupiter’s geography. I found something and that’s why Cathleen’s smug. Me, too.”

“Why latitude but nothing about longitude?”

“Because of the way Juno‘s orbit works. The spacecraft’s not hovering over the planet or even circling it like the ISS circles Earth. NASA wanted to minimize Juno‘s exposure to Jupiter’s intense magnetic and radiation fields. The craft spends most of its 53‑day orbit at extreme distance, up to millions of kilometers out. When it approaches, it screams in at about 41 kilometers per second, that’s 91 700 mph, on a mostly north‑to‑south vector so it sees all latitudes from a few thousand kilometers above the cloud‑tops. Close approach lasts only about three hours, for the whole planet, and then the thing is on its way out again. During that three hours, the planet rotates about 120° underneath Juno so we don’t have a straight vertical N‑S pass down the planet’s face. Gathering useful longitude data’s going to take a lot more orbits.”

“So you’re sayin’ Juno felt gravity glitches at all different angles going pole to pole, but only some of the angles going round and round.”

“Exactly.”

“So now explain the wiggle‑waggles.”

“They represent parts‑per‑million variations in the field pulling Juno towards Jupiter at each latitude. Where the craft is over a more massive region it’s pulled a bit inwards and Sy’s map shows that as a green bump. Over a lighter region Juno‘s free to move outward a little and the map shows a pink dip. Kaspi and company interpret the heaviness just north of the equator to be a dense inward flow of gas all around the planet. Maybe it is. Sy and I think the pink droplet south of the equator could reflect the Great Red Spot lowering the average mass at its latitude. Maybe it is. As always, we need more data, okay? Now I’ve got questions for you, Sy.”

“Shoot.”

“You built your map by multiplying each Jn‑shape by its Kaspi gravitational intensity then adding the multiplied shapes together. But you only used Jn‑shapes with integer names. Is there a J½?”

“Some mathematicians play with fractional J‑thingies but I’ve not followed that topic.”

“Understandable. Next question — the J‘s look so much like sine waves. Why not just use sine‑shapes?”

“I used Jn‑shapes because that’s how Kaspi’s group stated their results. They had no choice in the matter. Jn‑shapes naturally appear in spherical system math. The nice thing about Jn‑shapes is that n provides a sort of wavelength scale. For instance, J35 divides Jupiter’s pole‑to‑pole arc into 36 segments each as wide as Earth’s diameter. Here’s a plot of intensity against n.”

Adapted from Kaspi, Figure 2a

“Left to right, red light to blue.”

“Exactly.”

~ Rich Olcott

Zoning Out over Jupiter

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, Physics: Waves, UncategorizedLeave a comment

I’m nursing my usual mug of eye‑opener in Cal’s Coffee Shop when astronomer Cathleen and chemist Susan chatter in. “Morning, ladies. Cathleen, prepare to be even more smug.”

“Ooo, what should I be smug about?”

“Your Jupiter suggestion. Grab some coffee and a couple of chairs.” <screen‑tapping on Old Reliable> “Ready? First step — purple and violet. You’ll never see violet or purple light coming from a standard video screen.”

“He’s going spectrum‑y on us, right, Cathleen?”

“More like anti‑spectrum‑y, Susan. Purple light doesn’t exist in the spectrum. We only perceive that color when we see red mixed with blue like that second band on Sy’s display. Violet light is a thing in nature, we can see it in flowers and dyes and rainbows beyond blue. Standard screens can’t show violet because their LEDs just emit red, blue and green wavelengths. Old Reliable uses mixtures of those three to fake all its colors. Where are you going with this, Sy?””

“Deeper into Physics. Cast your eyes upon the squiggles to the right. The one in the middle represents the lightwave coming from purple‑in‑the‑middle. The waveform’s jaggedy, but if you compare peaks and troughs you can see its shape is the sum of the red and blue shapes. I scaled the graphs up from 700 nanometers for red and 450 for blue.”

“Straightforward spectroscopy, Sy, Fourier analysis of a complicated linear waveform. Some astronomers make their living using that principle. So do audio engineers and lots of other people.”

“Patience, Cathleen, I’m going beyond linear. Fourier’s work applies to variation along a line. Legendre and Poisson extended the analysis to—”

“Aah, spherical harmonics! I remember them from Physical Chemistry class. They’re what gives shapes to atoms. They’ve got electron shells arranged around the nucleus. Electron charge stays as close to the nucleus as quantum will let it. Atoms absorb light energy by moving charge away from there. If the atom’s in a magnetic field or near other atoms that gives it a z-axis direction then the shells split into wavey lumps going to the poles and different directions and that’s your p-, d– and f-orbitals. Bigger shells have more room and they make weird forms but only the transition metals care about that.”

The angular portion of the lowest-energy spherical harmonics
Credit: Inigo.quilez, under CCA SA 3.0 license
Adapted from Wieczorek and Meschede under CC BY-NC-ND 4.0

“Considering you left out all the math, Susan, that’s a reasonable summary. I prefer to think of spherical harmonics as combinations of wave shapes at right angles. Imagine a spherical blob of water floating in space. If you tap it on top, waves ripple down to the bottom and back up again and maybe back down again. Those are zonal waves. A zonal harmonic averages over all E‑W longitudes at each N‑S latitude. Or you could stroke the blob on the side and set up a sectorial wave pattern that averages latitudes.”

“How about center‑out radial waves?”

“Susan’s shells do that job. My point was going to be that what sine waves do for characterizing linear things like sound and light, spherical harmonics do for central‑force systems. We describe charge in atoms, yes, but also sound coming from an explosion, heat circulating in a star, gravity shaping a planet. Specifically, Jupiter. Kaspi’s paper you gave me, Cathleen, I read it all the way to the Results table at the tail end. That was the rabbit‑hole.”

“Oh? What’s in the table?”

“Jupiter’s zonal harmonics — J‑names in the first column, J‑intensities in the second. Jn‘s shape resembles a sine wave and has n zeroes. Jupiter’s never‑zero central field is J0. Jn increases or decreases J0‘s strength wherever it’s non‑zero. For Jupiter that’s mostly by parts per million. What’s cool is the pattern you see when you total the dominating Jeven contributions.”

Data from Kaspi, et al.

Cathleen’s squinting in thought. “Hmm… green zone A would be excess gravity from Jupiter’s equatorial bulge. B‘s excess is right where Kaspi proposed the heavy downflow. Ah‑HAH! C‘s pink deficit zone’s right on top of the Great Red Spot’s buoyant updraft. Perfect! Okay, I’m smug.”

~ Rich Olcott