Category: Physics

Two’s Company, Three Is Perturbing

On By rolcottIn Mathematics, Physics: Newton and Gravity, Space Travel, UncategorizedLeave a comment

Vinnie does this thing when he’s near the end of his meal. He mashes his pizza crumbs and mozzarella dribbles into marbles he rolls around on his plate. Mostly on his plate. Eddie hates it when one escapes onto his floor. “Vinnie, you lose one more of those, you’ll be paying extra.”

“Aw, c’mon, Eddie, I’m your best customer.”

“Maybe, but there’ll be a surcharge for havin’ to mop extra around your table.”

Always the compromiser, I break in. “How about you put on less sauce, Eddie?”

Both give me looks you wouldn’t want.
  ”Lower the quality of my product??!?”
    ”Adjust perfection??!?”

“Looks like we’ve got a three‑body problem here.” Blank looks all around. “You two were just about to go at it until I put in my piece and suddenly you’re on the same side. Two‑way interaction predictable results, three‑way interaction hard to figure. Like when Newton calculated celestial orbits to confirm his Laws of Gravity and Motion. They worked fine for the Earth going around the Sun, not so good for the Moon going around the Earth. The Sun pulls on the Moon just enough to play hob with his two‑body Earth‑Moon predictions.”

“Newton again. So how did he solve it?”

“He didn’t, not exactly anyway.”

“Not smart enough?”

“No, Eddie, plenty smart. Later mathematicians have proven that the three‑body problem simply doesn’t have a general exact solution.”

“Ah-hah, Sy, I heard weaseling — general?”

“Alright, Vinnie, there are some stable special cases. Three bodies at relative rest in an equilateral triangle; certain straight‑line configurations; two biggies circling each other and a third, smaller one in a distant orbit around the other two’s center of gravity. There are other specials but none stable in the sense that they wouldn’t be disrupted by a wobbly gravity field from a nearby star or the host galaxy.”

A special-case solution
to the three-body problem
by MaxwellMolecule,
licensed under CC ASA 4.0

“So if NASA’s mission planners are looking at a four‑body Sun‑Jupiter‑Europa‑Juno situation, what’re they gonna do? ‘Give up’ ain’t an option.”

“Sure not. There’s a grand strategy with variations. The oldest variation goes back to before the Egyptian builders and everybody still uses it. Vinnie, when you fly a client to Tokyo, do you target a specific landing runway?”

“Naw, I aim for Japan, contact ATC Narita when I get close and they vector me in to wherever they want me to land.”

“How about you, Eddie? How do you get that exquisite balance in your flavoring?”

“Ain’t easy, Sy. Every batch of each herb is different — when it was picked, how it was stored, even the weather while it was growing. I start with an average mix which is usually close, then add a pinch of this and a little of that until it’s right.”

“For both of you, the critical word there was ‘close’. Call it in‑flight course adjustments, call it pinch‑and‑taste, everybody uses the ‘tweaking’ strategy. It’s a matter of skill and intuition, usually hard to generalize and even harder to teach in a systematic fashion. Engineers do it a lot, theoretical physicists work hard to avoid it.”

“What’ve they got that’s better?”

” ‘Better’ depends on your criteria. The method’s called ‘perturbation theory’ and strictly speaking, you can only use it for certain kinds of problems. Newton’s, for instance.”

“Good ol’ Newton.”

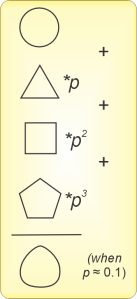
“Of course. Newton’s calculations almost matched Kepler’s planetary observations, but finagling the ‘not quite’ gave Newton headaches. More than 150 years passed before Laplace and others figured out how to treat a distant object as a perturbation of an ideal two‑body situation. It starts with calculating the system’s total energy, which wasn’t properly defined in Newton’s day. A perturbation factor p controls the third body’s contribution. The energy expression lets you calculate the orbits, but they’re the sum of terms containing powers of p. If p=0.1, p2=0.01, p3=0.001 and so on. If p isn’t zero but is still small enough, the p3 term and maybe even the p2 term are too small to bother with.”

“I’ll stick with pinch‑and‑taste.”

“Me and NASA’ll keep course‑correcting.”

~ Rich Olcott

Snap The Whip

On By rolcottIn Astronomy: Stellar Science, Physics: Electromagnetism, UncategorizedLeave a comment

“You say Alfven invented a whole science, Sy, but his double‑layer structures in plasma don’t look like much compared with the real ground‑breakers like Herschel or Hubble.”

“Your Astronomy bias is showing, Cathleen. The double‑layer thing was only a fraction what he gave to magnetohydrodynamics. To begin with, he dreamed up a new kind of wave.”

“There’s more than light waves, sound waves and ocean waves?”

“Certainly. There’s dozens of different kinds — look up waves in Wikipedia some day. Some move, some make other things move; sometimes things move in the direction the wave does, sometimes crosswise to it. From a Physics perspective waves are about repetition. Something that happens just once, where do you go from there?”

“That used to be Astronomy’s problem — only one solar system with fewer than a dozen planets, only two galaxies we could inspect closely. Now our space telescopes and monster‑mirror ground‑based observatories have given us thousands of planets and billions of stars and galaxies. If we get our classifications right we can follow an object type through every stage of development. It’s almost like watching Chemistry happen.”

“I doubt Susan Kim would agree but I get your point. Anyhow, most waves have a common underlying process. Many systems have an equilibrium condition. Doing something energetic like plucking on a guitar string moves the system away from equilibrium. That provokes some force to restore equilibrium. For the guitar, tension in the wire pulls it straight. Usually the restoration overshoots so the restoring force turns around to act in the opposite direction. That’s when the repetition starts, right?”

“Mm-hm, that’s sound waves in a nutshell. Ocean waves, too, because gravity’s the restoring force fighting with the wind to pull things flat.”

“Same idea. Well, Alfven’s first trick was to demonstrate that in a plasma or any conducting medium, a magnetic field acts like that guitar string. The field’s equilibrium configuration is straight and smooth. If you perturb the medium somehow to put a bend or kink in the field, magnetic tension kicks in to restore equilibrium. Waves restored by magnetic fields are important enough that they’re now called Alfven waves in his honor.”

“First trick, mmm? There’s more?”

“Yup, an old one he borrowed from Maxwell — the flux tube. Maxwell worked before atoms were a conceptual thing. He thought about magnetism in terms of immaterial ‘lines of force’ that followed the rules laid out in his equations. Think of grabbing a handful of barely cooked spaghetti, still mostly stiff.”

“Yuck.”

“You’re wearing gloves, okay? The point is, you’ve got a more‑or‑less cylindrical bundle of parallel strands. Pretend each strand is a line of magnetic force. Maxwell’s rules say the number of lines of force, the total magnetic flux, coming out one end of the bundle exactly equals the flux that went in the other end. There’s no sourcing or destroying magnetic flux in between.”

“What if I squeeze real hard?”

“Nope. The flux per unit area intensifies — that’s called ‘the pinch effect’ and particle beam folks love it — but the total flux stays the same. Here’s where it gets interesting. Alfven showed that if the flux tube passes through a plasma or other conducting medium, the medium’s charged particles get frozen into the field. Waggle the field, you waggle the particles. Now put that together with his waves.”

“Oh, that’s what those guys have been talking about! There’s a slew of recent papers built on observations from the Parker Solar Probe mission. One of the biggest outstanding problems in solar physics is, how can the corona, the outermost layer of the Sun’s atmosphere, be millions of degrees hotter than the 6000‑degree photosphere beneath it? Well, PSP and other satellite missions have recorded many observations where the ambient magnetic field suddenly flipped from one direction to its near‑opposite. It’s like the probe had flown through a flux tube zig‑zag in space.”

“Those sharp angles indicate a lot of pent‑up magnetic tension.”

“Absolutely! Now imagine those zig‑zags in the crowded chaos inside the Sun’s atmosphere, colliding, criss‑crossing, disconnecting, reconnecting, releasing their magnetic flux energy into frozen‑in particles that aren’t frozen any more. What do you get, Sy?”

“Immense amounts of kinetic energy. Hot times, indeed”

~ Rich Olcott

Why Those Curtains Ripple

On By rolcottIn Astronomy: Planetary Science, Physics: Electromagnetism, UncategorizedLeave a comment

I’m in the scone line at Cal’s Coffee when suddenly there’s a too‑familiar poke at my back, a bit right of the spine and just below the shoulder blade. I don’t look around. “Morning, Cathleen.”

“Morning, Sy. Your niece Teena certainly likes auroras, doesn’t she?”

“She likes everything. She’s the embodiment of ‘unquenchable enthusiasm.’ At that age she’s allowed.”

“It’s a gift at any age. Some of the kids in my classes, they just can’t see the wonders no matter how I try. I show them aurora photos and they say, ‘Oh yes, red and green in the sky‘ and go back to their phone screens. Of course there’s no way to get them outside late at night at a location with minimal light pollution.”

“I feel your pain.”

“Thanks. By the way, your aurora write-ups have been all about Earth’s end of the magnetic show. When you you going to do the rest of the story?”

“How do you mean?”

“Magnetism on the Sun, how a CME works, that sort of thing.”

“As a physicist I know a lot about magnetism, but you’re going to have to educate me on the astronomy.”

Plane‑polarized Lorentz (electromagnetic) wave
 Electric (E) component is red
 Magnetic (B) component is blue
(Image by Loo Kang Wee and Fu-Kwun Hwang from Wikimedia Commons)
Licensed under CC ASA3.0 Unported

“Deal. You go first.”

<displaying an animation on Old Reliable> “We’ll have to flip between microscopic and macroscopic a couple times. Here’s the ultimate micro — a single charged particle bouncing up and down somewhere far away has generated this Lorentz‑force wave traveling all alone in the Universe. The force has two components, electric and magnetic, that travel together. Neither component does a thing until the wave encounters another charged particle.”

“An electron, right?”

“Could be but doesn’t have to be. All the electric component cares about is how much charge the particle’s carrying. The magnetic component cares about that and also about its speed and direction. Say the Lorentz wave is traveling east. The magnetic component reaches out perpendicular, to the north and south. If the particle’s headed in exactly the same direction, there’s no interaction. Any other direction, though, the particle’s forced to swerve perpendicular to both the field and the original travel. Its path twists up- or downward.”

A charged particle traversing a Lorentz wave

“But if the particle swerves, won’t it keep swerving?”

“Absolutely. The particle follows a helical path until the wave gives out or a stronger field comes along.”

“Wait. If a Lorentz wave redirects charge motion and moving charges generate Lorentz waves, then a swerved particle ought to mess up the original wave.”

“True. It’s complicated. You can simplify the problem by stepping back far enough that you don’t see individual particles any more and the whole assembly looks like a simple fluid. We’ve known for centuries how to do Physics with water and such. Newton invented hydrodynamics while battling the ghost of Descartes to prove that the Solar System’s motion was governed by gravity, not vortices in an interplanetary fluid. People had tried using Newton‑style hydrodynamics math to understand plasma phenomena but it didn’t work.”

<grinning> “I don’t imagine it would — all that twistiness would have thrown things for a loop.”

“Haha. Well, in the early 1940s Swedish physicist Hannes Alfven started developing ideas and techniques, extending hydrodynamics to cover systems containing charged particles. Their micro‑level electromagnetic interactions have macro‑level effects.”

“Like what?”

“Those aurora curtains up there. Alfven showed that in a magnetic field plasmas can self‑organize into what he called ‘double layers’, pairs of wide, thin sheets with positive particles on one side against negative particles in the other. Neither sheet is stable on its own but the paired‑up structure can persist. Better yet, plasma magnetic fields can support coherent waves like the ones making that curtain ripple.”

“Any plasma?”

“Sure.”

“Most of the astronomical objects I show my students are associated with plasmas — the stars themselves, of course, but also the planetary nebulae that survive nova explosions, the interstellar medium in galactic star‑forming regions, the Solar wind, CMEs…”

“Alfven said we can’t understand the Universe unless we understand magnetic fields and electric currents.”

~ Rich Olcott

Colors Made of Air

On By rolcottIn Astronomy: Planetary Science, Physics: Electromagnetism, UncategorizedLeave a comment

Teena’s whirling around in the night with her head thrown back. “I LUVV AURORAS!! They’re SO beautiful beautiful beautiful!”

“Yes, they are, Teena. They’re beautiful and magical, and for me it’s even better because they’re Physics at work right in front of us. Well, above us.”

“Oh, Sy, give it a rest.”

“No, really, Sis. I look at a rainbow and I’m dazzled by its glory against the rainclouds but I’m also aware that each particular glimpse of pure color comes to me by refraction through one individual droplet. Better yet, I appreciate the geometry that presents the entire spectrum in perfectly circular arcs. Marvels supported by underlying marvels. These curtains are another example of beauty emerging from hidden sources.”

“What do you mean?”

“Remember Teena’s teacher’s magnetic force lines that were organized and revealed by iron filings? Auroras are a bit like that, except one level deeper. Again we don’t see magnetic fields directly. What we do see is light coming to us from oxygen and nitrogen atoms that are bombarded by rampaging charged particles.”

“Wait, Uncle Sy, we learned that charges make magnetic fields when they move.”

“That, too. It works both ways, which is why they call it electromagnetism. A magnetic field steers protons and electrons which make their own field to push back on the first one. But my point is, the colors in each curtain and the curtains themselves tell us about the current state of the atmosphere and Earth’s magnetic field.”

“Okay, I can see how magnetic fields up there could steer charged particles to certain parts of the sky, but how does that tell us about the atmosphere? What do the colors have to do with it? Is this more rainbows and geometry?”

“Definitely not. Sis. Rainbows are sunlight refracted through water droplets. Aurora light’s emitted by atoms in our own atmosphere. Each color is like a fingerprint of a specific atom in specific circumstances. The uppermost reds, for instance come from oxygen atoms that rarely touch another atom of any kind. They’re at 150 or more kilometers altitude, way above the stratosphere. There aren’t many of them that far up which is why the curtain tops sort of fade away into infinity.”

Aurora, photo by AstroAnthony
licensed under CC BY-SA 4.0

“Oooo, now it’s going green and yellow!”

“Mm-hm, the bombardment’s reaching further now. Excited oxygen atoms emit green lower down in the atmosphere where collisions happen more often and don’t give the red‑emitters a chance to do their thing. The in‑between yellow isn’t really there — it’s what your eye tells you when it sees pure red and pure green overlapping.”

“Why do the curtains have that sharp lower edge, Sy? Surely we don’t run out of oxygen there.”

“Quite the reverse. That level’s about 100 kilometers up. It’s where the atmosphere gets so thick that collisions drain away an excited atom’s energy before it gets a chance to shine.”

“But why are there curtains at all? Why not simply fill the sky with a smooth color wash?”

IMAGE view of Aurora australis
Credit: NASA, public domain

“Mars gets auroras like that, or at least Perseverance just spotted one. We don’t, thanks to our well‑ordered magnetic field. Mars’ field is lumpy and too weak to funnel incoming charged particles to special spots like our poles. Actually, those curtains are just segments of rings that go all around Earth’s magnetic axis. The rings usually lurk about 2/3 of the way to our poles but a really strong solar event like this one can push them closer to the Equator.”

“Mars gets auroras? Uncle Sy, how about other planets?”

“Them, too, but theirs mostly don’t look like ours. You’d have to be able to see X‑rays on Mercury, for instance. Venus gets a general green glow for the same reason that Mars does. Jupiter is Texas for the Solar System — everything’s bigger there, including auroras in every color from X‑ray to infrared. Strong ordered field, so I’m sure there’s curtains up there.”

Sis yanks out her writer’s‑companion notebook and scribbles without looking down…
  ”Curtains made of colors
   Colors made of air.“

Aurora, photo by Bellezzasolo
licensed under CC BY-SA 4.0

~ Rich Olcott

Sky Lights

On By rolcottIn Astronomy: Planetary Science, Physics: Electromagnetism, UncategorizedLeave a comment

“Mom! Uncle Sy! Come outside NOW before it goes away!”

“Whah— oooh!”
 ”An aurora! Thanks for calling us.”

“Glowing curtains rippling across the sky! Spotlights shining down through them! Where do those come from?”

“From the Sun, Teena.”

“C’mon, Sy. The Sun’s 93 million miles away. Even if that bright streak up there is as much as 10 miles across, which I doubt, the beam from the Sun would be only a teeny‑tiny fraction of a degree wide. Not even magnetars send out anything that narrow.”

“Didn’t say it’s a beam, Sis. The whole display comes from the Sun as single package. Sort of. Sometimes.”

“Even for you, little brother, that’s a new level of weasel‑wording.”

“Well, it’s complicated.”

“So unravel it. Start from the beginning.”

“Okay. The Sun’s covered in plasma—”

“Eww!”

“Not that kind of plasma, Teena. This is mostly hydrogen atoms except they’re so hot that the electrons and protons break away from each other and travel separately. What have they told you in school about magnets?”

“Not much. Umm … electric currents push on magnets and that’s how motors work, and magnets push on electrons and that’s how a generator works. Oh, and Mr Cox laid a sheet of paper on top of a magnet and sprinkled iron filings on it so we could see the lines of force, but when I asked him what made the magnetism ’cause I didn’t see any wires he started talking about electrons in iron atoms and then the bell rang and I had to go to Spanish class.”

The shape of the bar magnet’s field, disclosed by iron filings chaining together.

<sigh> “The clock rules, doesn’t it? Anyway, he was on the right track, but I want to get back to those lines of force. Were they there before he sprinkled on those filings?”

“Mmm … Mom would say, ‘That’s a good question,’ but how could you know? I’m gonna say they were.”

“Your Mom would be right, but sorry, you’re wrong. With no iron filings in the picture, the magnetic field is nice and smooth, everywhere just the same or maybe only a little bit stronger or weaker than neighboring points. No lines. Conditions change when you put the first bit of iron anywhere in the field. As Mr Cox was probably saying when the bell interrupted, the electrons in the grain’s iron atoms align orbitals with the magnetic field. The alignment affects the surrounding field and that pulls in other iron bits that change the field even more.”

“But wouldn’t that make just a solid iron blob?”

“No, because a magnetic field has both strength and direction. Once the first particle points along the field, the iron bits it recruits rotate to point mostly in the same direction. You wind up with a chain of specks tracing out where they’ve acted together to alter the field. The chain’s surrounded by spaces where the field’s been stressed.”

“And then lotsa chains make lotsa lines, yeah!”

“I see where you’re headed, Sy. You’re going to claim that the vertical lines we see in the curtains trace out the Sun’s magnetic field.”

“Not quite, Sis. There’s only one magnetic field, a combination of Earth’s field, the Sun’s field, and the magnetic fields contained in whatever the Sun throws our way. Way out here Earth’s field is about ten thousand times stronger than the Sun’s is, but the fields inside a CME can range up to 10% or 20% of Earth’s. The moving curtains up there are the result of a magnetic tussle between us and a CME or maybe a flare’s outflow.”

CME blast (red‑orange) impacting Earth ‘s magnetic field (blue lines)
Credit: NASA/GSFC/SOHO/ESA

“But there aren’t any iron filings up there, Uncle Sy!”

“True, but there are free charged particles in the ionosphere thanks to UV radiation from the Sun. A free electron caught in a magnetic field whips into a tight spiral. Its field gets neighbor particles spiraling. Pretty soon you wind up with a chain of them spiraling together, lining up like the filings do.”

“The spotlights?”

“Probably ion blobs embedded in the CME, but that’s a guess.”

Aurora, photo by W.carter
licensed under CC BY-SA 4.0

~ Rich Olcott

A Play Beyond The Play

On By rolcottIn Cosmology, Gravitational astronomy, Uncategorized, Vera RubinLeave a comment

Vinnie takes a long thoughtful look at the image that had dashed his beautiful six‑universe idea. “Wait, Sy. I don’t like this picture”

“Because it messes up your invention?”

“No, because how can they know what that halo looks like? I mean, the whole thing with dark matter is that we can’t see it.”

“You’re right about that. Dark matter’s so transparent that even with five times more mass than normal matter, it doesn’t block CMB photons coming from 13.8 billion lightyears away. That still boggles my brain every once in a while. But dark matter’s gravitational effects — those we can see.”

“Yeah, I remember a long time ago we talked about Fritz Zwicky and Vera Rubin and how they told people about galaxies held together by too much gravity but nobody believed them.”

“Well, they did, after a while—”

“A long while, like a long while since those talks. Remind me what ‘too much gravity’ was about.”

“It was about conflicts between their observations and the prevailing theoretical models. Everyone thought that galaxies and galaxy clusters should operate pretty much like planetary orbits — your speed increases the closer you are to the center, up to Einstein’s speed limit. Newton’s Laws of Motion predict how fast you should move if you’re at a certain distance from a body with a certain mass. If you’re moving faster than that, you fly away.”

“Yeah, escape velocity. So the galaxies in Zwicky’s cluster didn’t follow Newton’s Laws?”

“They didn’t seem to. Galaxies that should have escaped were still in there. The only way he could explain the stability was to suppose the galaxies are only a small fraction of the cluster’s mass. Extra gravity from the extra mass must bind things together. Forty years later Rubin’s improved technology revealed that stars within galaxies had the same anomalous motion.”

“I’m guessing the ‘faster near the center’ rule didn’t hold, or else you wouldn’t be telling this story. Spun like a wheel, I bet.”

“When a wheel spins, every part of it rotates at the same angular speed, the same number of degrees per second, right?”

“Ahh, the bigger my circle the higher my airspeed so the rule would be ‘faster farther out’.”

“That’s the wheel rule, right, but Rubin’s data showed that stars within galaxies don’t obey that one either. She measured lots of stars in Andromeda and other galaxies. Their linear speeds, kilometers per second, are nearly identical from near the center all the way out. Even dust and gas clouds beyond the galactic starry edges also fit the ‘same linear speed everywhere’ rule. You’d lose the bet.”

“That just doesn’t feel right. How can just gravity make that happen?”

“It can if the right amount of dark matter’s distributed in the right‑shaped smeared‑out hollowed‑out spherical halo. The halo’s radial density profile looks about like this. Of course, profiles for different galaxies differ in spread‑outness and other details, but the models are pretty consistent.”

“Wait, if dark matter only does gravity like you said, why’s that hole in the middle? Why doesn’t everything just fall inward?”

“Dark matter has mass so it also has inertia, momentum and angular momentum, just as normal matter does. Suppose some of the dark matter has collected gravitationally into a blob and the blob is moving slower than escape velocity. If it’s flying straight at the center of gravity it’ll get there and stay there, more or less. But if the blob’s aimed in any other direction, it has angular momentum relative to the center. Momentum’s conserved for dark matter, too. The blob eventually goes into orbit and winds up as part of the shell.”

“Does Zwicky’s galaxy cluster have a halo, too?”

“Not in the same way. Each galaxy probably has its own halo but the galaxies are far apart relative to their size. The theoreticians have burned huge amounts of computer time simulating the chaos inside large ensembles of gravity‑driven blobs. I just read one paper about a 4‑billion‑particle calculation and mind you, a ‘particle’ in this study carried more than a million solar masses. Big halos host subhalos, with filaments of minihalos tying them together. What we can’t see is complicated, too.”

~ Rich Olcott

Rows, Columns And Freedom

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Geez, Sy. You know I hate equations. I was fine with the Phase Rule as an arithmetic thing but you’ve thrown so much algebra at me I’m flummoxed. How about something I can visualize?”

“Sorry, Vinnie, the algebra was just to show where the Rule came from. Application’s not in my bailiwick. Susan, it’s your turn.”

“Sure, Sy, this is Chemistry. Okay, Vinnie, what’s the Rule about?”

“Degrees of freedom, but I’m still not sure what that means. ‘Independent intensive variables’ doesn’t say much to me.”

“Understandable, seeing as you don’t like equations. Visualize a spreadsheet. There’s an ‘Energy’ header over columns A and B. The second row reads ‘Name’ and ‘Value’ in those two columns. Then one row each for Temperature and Pressure.”

“This is more like it. Any numbers in the value column?”

“Not yet. They’ll be degrees of freedom, maybe. Next, ‘Components‘ in cell C1, ‘Name’ in C2 and then C rows, one for each component.”

“Do we care how much of each component?”

“Not yet.* Next visualize a multi‑column ‘Phases‘ header over one column for each phase. The second row names the phase. Below that there’s a row for each component. The whole array is for figuring how each component spreads across the phases assuming there’s enough of everything to reach equilibrium. With me?”

“A little ahead, I think. Take one of Kareem’s lava pools on Io, for instance. It’s got two components, iron and sulfur, and two molten phases, iron‑light 5:95 floating on top of iron‑heavy 60:40. Phase Rule says the freedom degrees is C–P+2=2–2+2, comes to 2 but that disagrees with the 6 open boxes I see.”

“But the boxes aren’t independent. Think of the interface between the two phases. One by one, atoms in each phase wander across to the other side. At equilibrium the wandering happens about as often in both directions.”

Adapted from Walder and Pelton
Click image to expand

“That’s your reversibility equilibrium.”

“Right, thermodynamics’ classic competition between energy and entropy — electronic energy holding things together against entropy flinging atoms everywhere. Pure iron’s a metallic electron soup that can accept a lot of sulfur without much disturbance to its energy configuration. That means sulfur’s enthalpy doesn’t differ much between the two environments and that allows easy sulfur traffic between the two phases. On the other hand, pure sulfur will accept only a little iron because iron disrupts sulfur‑sulfur moleular bonding. Steep energy barrier against iron atoms drifting into the 95:5 phase; low barrier to spitting them out. Kareem’s phase diagram for atmospheric pressure shows how things settle out for each temperature. There’s a neat equation for calculating the concentration ratios from the enthalpy differences, but you don’t like equations.”

“You’re right about that, Susan, but I smell weaseling in your temperature‑pressure dodge.”

Water’s phase diagram

“Not really. You’ve read Sy’s posts about enthalpy’s internal energy, thermal and PV‑work components. Heat boosts entropy’s dominance and tinkers with the enthalpies.”

Meanwhile, I’ve been tapping Old Reliable’s screen. “I’m playing water games over here. Maybe this will help clarify the freedom. Water can be ice, liquid or vapor. At high temperature and pressure, the liquid and gas phases become a single phase we call supercritical. Here’s a sketch of water’s phase diagram. Only one component so C=1 … and a spreadsheet summarizing seven conditions.

“The first four are all at atmospheric pressure, starting at position 1 — just water vapor in a single phase so P=1, DF=2. We can change temperature and pressure independently within the phase boundaries. If we chill to point 2 liquid water condenses. If we stop there, on the boundary, we’re at equilibrium. We could change temperature and still be at equilibrium, but only if we change pressure just right so we stay on that dotted line. The temperature‑pressure linkage constraint leaves us only one degree of freedom — along the line.”

“Ah, 3 and 5 work the same way as 1 but for liquid and solid, and 4‘s like 2. The Fixed ones—?”

“One unique temperature‑pressure combination for each equilibrium. No freedoms left.”

  • * Given specific quantities of iron and sulfur, chemists can calculate equilibrium quantities for each phase. Susan assigned that as a homework problem once.

~ Rich Olcott

The Quest for Independents

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

The thing about Vinnie is, he’s always looking for the edges and loopholes. He’d make a good scientist or lawyer but he’s happy flying airplanes. “Guys, I heard a lot of dodging when you started talking about that Gibbs Rule. You said it only works when things are in equilibrium. That’s what Susan was talking about when she said Loki Lake on Io ain’t an equilibrium ’cause there’s stuff getting pumped in and going away so the equations don’t balance. I got that. But then you threw in some other excepts, like no biology or other kinds of work. What’s all that got to do with the phases and chemistry?”

“They’re different processes that drive a system away from equilibrium. Biology, for example. Every kind of life taps energy sources to maintain unstable structures. Proteins, for instance — chemically they’re totally unstable. Oxidation, random acid‑base reactions, lots of ways to degrade a protein molecule’s structure until its atoms wind up in carbon dioxide and nitrogen gas. Your cells, though, they continually burn your food for energy to protect old protein molecules or build new ones and DNA and bones and everything. I visualize someone riding a bicycle up a hillside of falling bowling balls, desperately fighting entropy just to keep upright.”

“Fearsome image, Susan, but it fits. From a Physics perspective, dumping in or extracting any kind of work disrupts any system that’s at equilibrium. The Phase Rule accounts for pressure-volume energy because that’s already part of enthalpy—”

“Wait, Sy, I don’t see pressure‑volume or even ‘PV‘ in
  ’degrees of freedom=components–phases+2‘.”

“That’s what the ‘2′ is about, Vinnie. If it weren’t for pressure‑volume energy, that two would be a one.”

“C’mon.”

“No, really. ‘Degrees of freedom’ counts the number of intensive properties that are independent of each other. Neither temperature nor pressure care about how much of something you’ve got, so they’re both intensive properties. Temperature’s always there so that’s one degree of freedom. If PV energy’s part of whatever process you’re looking at, then pressure comes into the Rule by way of the enthalpies we use to calculate equilibrium situations. I guess you could write the Rule as
  DF=C–P+1T+1PV.“

“That’s not the way we learned that in school, Sy. It was
  DF=C–P+1+N,
with ‘N’ counting the number of work modes — PV, gravitational, electrical, whatever fits the problem.”

“How would you do gravitational work on an ice cube, Kareem?”

“Wouldn’t be a cube, Vinnie, it’d be a parcel of Jupiter’s atmosphere caught in a kilometers‑high vertical windstream. Water ice, ammonia ice, ammonium polysulfide solids, all in a hydrogen‑helium medium. A complicated problem; whoever picks it up will have to account for gravity and pressure effects.”

“Come to think of it, the electric option is getting popular and Kareem’s iron‑sulfur system may be a big player. My Chemistry journals have carried a sudden flurry of papers about iron‑sulfur batteries as cheap, safe alternatives to lithium‑based designs for industry‑sized storage where low weight isn’t a consideration. Battery voltage is intensive, doesn’t care about size. Volt’s extensive ‘how much’ buddy is amps. Electrical work is volts times amps so it fits right in with the Rule if I write
  DF=C–P+1T+1PV+1VA
A voltage box with sulfur electrodes on one side and iron electrodes on the other would be way out of equilibrium.”

“But why components minus phases? Why not times? What if it comes out negative? What’d that even mean?”

Water’s phase diagram

“Fair questions, Vinnie. Degrees of freedom counts independent properties, right? You’d think the phases‑components contribution to DF would be P*C but no. The component percentages in C must total 100%. If you know all but one percentage, the last percentage isn’t independent. Same logic applies to the P phases. That leaves (C–1) and (P–1) independent variables. For the P phases P*C drops to P*(C–1) variables. But you also know that each component is in equilibrium across all phases. Each equilibrium reduces the count by one, for C*(P–1) reductions. Do the subtraction
  P*(C–1)–C*(P–1)=C–P
You’re left with only C–P quantities that can change without affecting other things. If the result’s negative it’ll constrain exactly that many other intensive variables, like with water’s triple point.”

~ Rich Olcott

Water Rites

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Vinnie pulls a chair over to our table, grabs some paper napkins for scribbling. “You guys know I hate equations, but this Phase Rule one is simple enough even I can play. It says ‘degrees of freedom’ equals ‘components’ minus ‘phases’ plus 2, right? Kareem’s phase diagram has a blue piece with a slush of iron crystals floating in an iron‑sulfur melt. There’s two components, iron and sulfur, two phases, crystals and melt, so the degrees come to 2–2+2=2 and that means we get to choose any two, you said intensive properties, to change. Do I got all that straight, tell me more about degrees and what’s intensive?”

Phase diagram for the iron:sulfur system
Adapted from Walder and Pelton
Click image to expand

“Good job, Vinnie, and good questions. Extensive properties are about how much. In Kareem’s experiment, he’s free to add iron or sulfur in whatever quantities he wants. By contrast, intensive properties don’t care about how much is there. The equilibrium melt’s iron:sulfur ratio stays between zero and one whatever the size of Kareem’s experiment. The ratio’s an intensive property. So are temperature and pressure. If he kept his experimental pressure constant but raised the temperature, I expect some of the crystals would dissolve. That’d lift the iron:sulfur ratio.”

“How about raising the pressure, Kareem?”

“I suspect that’d squeeze iron back into the crystalline mass, but I’ve not tried that so I don’t know. Different materials behave different ways. Raising the pressure on normal water ice melts it, which is why ice skates work.”

Susan suddenly pulls her tablet from her purse and starts fiddling with it.

“Fair enough. Okay, in your diagram’s top yellow piece where it’s all molten, there’s still 2 components but one phase so the Rule goes 2–1+2=3. You’re saying 3 degrees means you can choose whatever temperature, pressure and mix ratio you want and it’d still be molten.”

“You’ve got the idea, Vinnie. What I’m really interested in, though, is what happens when I add more components. To model Io’s lava pools I need to roll in oxygen and silicon from the surrounding rocks. I’m looking at a 4‑component situation which could have multiple phases and things are complicated”

Vinnie’s got that ‘gotcha’ glint in his eye. “Understood. But how about going in the other direction? If you’ve got only one component then you could have either 1–2+2=1 or 1–3+2=0. How do either of those make sense?”

Susan shows a display on her tablet. “As soon as Kareem mentioned ice I figured this phase diagram would come in handy. It’s for water — single component so there’s no variation along a component axis, just pressure and temperature.”

“Kareem had to read his chart to us. Now it’s your turn.”

“Of course. By convention, pressure’s on the y‑axis, temperature’s along the x‑axis. The pressure range is so wide that this chart uses a logarithmic scale which is why the distances look weird. Over there on the cold side, there’s two kinds of ice. Ice Ic has a cubic crystal structure. Warm it up past 240K and it converts to a hexagonal form, Ice Ih. That’s the usual variety that makes snowflakes.”

“TP!” <snirk, snirk>

“Cal, please. That’s water’s Triple Point, Vinnie’s 1–3+2=0 situation where all three phases are in equilibrium with each other so there’s no degrees of freedom. The solid‑liquid and liquid‑vapor boundaries are examples of Vinnie’s 1–2+2=1 condition — only one degree of freedom, which means that equilibrium temperature and pressure are tightly linked together. Squeeze on ice, its melting point drops, so we ice skate on a thin film of liquid water. Normal Boiling Point holds at standard atmospheric pressure but if you heat water while up on a balloon ride it may not get hot enough to hard‑boil those eggs you brought for the picnic.”

“What’s going on in the gray northeast corner?”

“CP‘s the Critical Point at the end of the 1–2+2=1 line. The liquid-vapor surface disappears. No gas or liquid in the container, just opalescent supercritical fog. There’s only one phase; temperature and pressure are independent. Beyond CP you’re in 1–1+2=2 territory.”

~ Rich Olcott

Surf Lake Loki? No, Thanks.

On By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Vinnie’s been eavesdropping (he’s good at that). “You guys said that these researcher teams looked at how iron and sulfur play together at a bunch of different temperature, pressures and blend ratios. That’s a pretty nice chart, the one that shows mix and temperature. Got one for pressure, like the near‑vacuum over Loki’s lava lake on Io?”

“Not to my knowledge, Vinnie. Of course I’m a lab chemist, not a theoretical astrogeochemist. Kareem’s phase diagram is for normal atmospheric pressure. I’d bet virtually all related lab work extends from there to the higher pressures down toward Earth’s center. Million‑atmosphere experiments are difficult — even just trying to figure out whether a microgram sample’s phase in a diamond anvil cell is solid or liquid. Right, Kareem?”

“Mm‑hm, but the computer work’s hard, too, Susan. We’ve got several suites of software packages for modeling whatever set of pressure-temperature-composition parameters you like. The problem is that the software needs relevant thermodynamic data from the pressure and temperature extremes like from those tough‑to‑do experiments. There’s been surprises when a material exhibited new phases no‑one had ever seen or measured before. Water’s common, right, but just within the past decade we may have discovered five new high‑pressure forms of ice.”

“May have?”

Artist’s concept of Loki Patera,
a lava lake on Jupiter’s moon Io
Credit: NASA/JPL-Caltech/SwRI/MSSS

“The academics are still arguing about each of them. Setting aside that problem, modeling Io’s low‑pressure environment is a challenge because it’s not a lab situation. Consider Cal’s pretty picture there. See those glowing patches all around the lava lake’s shore? They’re real. Juno‘s JIRAM instrument detected hot rings around Loki and nearly a dozen of its cousins. Such continual heat release tells us the lakes are being stirred or pumped somehow. Whatever delivers heat to the shore also must deliver some kind of hot iron‑sulfur phase to the cooler surface. That’ll separate out like slag in a steel furnace.”

“It’s worse than that, Kareem. Sulfur’s just under oxygen in the periodic table, so like oxygen it’s willing to be gaseous S2. Churned‑up hot lava can’t help but give off sulfur vapor that the models will have to account for.”

I cut in. “It’s worse than that, Susan. I’ve written about Jupiter’s crazy magnetic field, off‑center and the strongest of any planet. Io’s the closest large moon to Jupiter, deep in that field. Sulfur molecules run away from a magnetic field; free sulfur atoms dive into one. Either way, if you’re some sulfur species floating above a lava lake when Jupiter’s field sweeps past, you won’t be hanging around that lake for long. Most likely, you’ll join the parade across the Io‑to‑Jupiter flux tube bridge.”

Susan chortles. “Obviously not an equilibrium. It’s a steady state!”

“Huh?” from everyone. Cal gives her, “Steady state?”

“Chemical equilibrium is when a reaction and its reverse go at equal rates, right, so the overall composition doesn’t change. That’s the opposite of situations where there’s a forward reaction but for some reason the products don’t get a chance to back‑react. Classic case is precipitation, say when you bubble smelly H2S gas through a solution that may contain lead ions. If there’s lead in there you get a black lead sulfide sediment that’s so insoluble there’s no re‑dissolve. Picture an industrial vat with lead‑contaminated waste water coming in one pipe and H2S gas bubbling in from another. If you adjust the flow rates right, all the lead’s stripped out, there’s no residual stink in the effluent water and the net content of the vat doesn’t change. That’s a steady state.”

“What’s that got to do with Loki’s lake?”

“Sulfur vapors come off it and those glowing rings tell us it’s giving off heat. It’s just sitting there not getting hotter and probably not changing much in composition. There’s got to be sulfur and heat inflow to make up for the outflow. The lake’s in a steady state, not an equilibrium. Thermodynamic calculations like Gibbs’ phase rule can’t tell you anything about the lake’s composition because that depends on the kinetics — how fast magma comes in, how fast heat and sulfur go out. Kareem’s phase diagram just doesn’t apply.”

~ Rich Olcott