Category: Physics: Newton and Gravity

Three ways to look at things

On By rolcottIn Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Fundamentals, Physics: Light and Relativity, Physics: Newton and Gravity, UncategorizedLeave a comment

A familiar shadow loomed in from the hallway.

“C’mon in, Vinnie, the door’s open.”

“I brought some sandwiches, Sy.”

“Oh, thanks, Vinnie.”

“Don’t mention it.    An’ I got another LIGO issue.”

“Yeah?”

“Ohh, yeah.  Now we got that frame thing settled, how does it apply to what you wrote back when?  I got a copy here…”

The local speed of light (miles per second) in a vacuum is constant.  Where space is compressed, the miles per second don’t change but the miles get smaller.  The light wave slows down relative to the uncompressed laboratory reference frame.

“Ah, I admit I was a bit sloppy there.  Tell you what, let’s pretend we’re piloting a pair of space shuttles following separate navigation beams that are straight because that’s what light rays do.  So long as we each fly a straight line at constant speed we’re both using the same inertial frame, right?”

“Sure.”

“And if a gravity field suddenly bent your beam to one side, you’d think you’re still flying straight but I’d think you’re headed on a new course, right?”

“Yeah, because now we’d have different inertial frames.  I’d think your heading has changed, too.”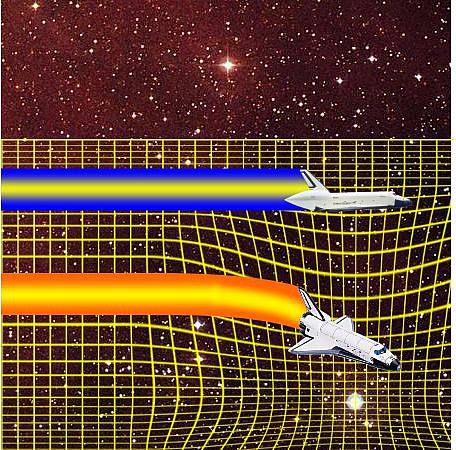two-shuttles

“So what does the guy running the beams see?”

“Oh, ground-pounders got their own inertial frame, don’t they?  Uhh… He sees me veer off and you stay steady ’cause the gravity field bent only my beam.”

“Right — my shuttle and the earth-bound observer share the same inertial frame, for a while.”

“A while?”

“Forever if the Earth were flat because I’d be flying straight and level, no threat to the shared frame.  But the Earth’s not flat.  If I want to stay at constant altitude then I’ve got to follow the curve of the surface rather than follow the light beam straight out into space.  As soon as I vector downwards I have a different frame than the guy on the ground because he sees I’m not in straight-line motion.”

“It’s starting to get complicated.”

“No worries, this is as bad as it gets.  Now, let’s get back to square one and we’re flying along and this time the gravity field compresses your space instead of bending it.  What happens?  What do you experience?”

“Uhh… I don’t think I’d feel any difference.  I’m compressed, the air molecules I breath are compressed, everything gets smaller to scale.”

“Yup.  Now what do I see?  Do we still have the same inertial frame?”

“Wow.  Lessee… I’m still on the beam so no change in direction.  Ah!  But if my space is compressed, from your frame my miles look shorter.  If I keep going the same miles per second by my measure, then you’ll see my speed drop off.”

“Good thinking but there’s even more to it.  Einstein showed that space compression and time dilation are two sides of the same phenomenon.  When I look at you from my inertial frame, your miles appear to get shorter AND your seconds appear to get longer.”

“My miles per second slow way down from the double whammy, then?”

“Yup, but only in my frame and that other guy’s down on the ground, not in yours.”

“Wait!  If my space is compressed, what happens to the space around what got compressed?  Doesn’t the compression immediately suck in the rest of the Universe?”

“Einstein’s got that covered, too.  He showed that gravity doesn’t act instantaneously.  Whenever your space gets compressed, the nearby space stretches to compensate (as seen from an independent frame, of course).  The edge of the stretching spreads out at the speed of light.  But the stretch deformation gets less intense as it spreads out because it’s only offsetting a limited local compression.”

“OK, let’s get back to LIGO.  We got a laser beam going back and forth along each of two perpendicular arms, and that famous gravitational wave hits one arm broadside and the other arm cross-wise.  You gonna tell me that’s the same set-up as me and you in the two shuttles?”

“That’s what I’m going to tell you.”

“And the guy on the ground is…”

“The laboratory inertial reference.”

“Eat your sandwich, I gotta think about this.”

(sounds of departing footsteps and closing door)

“Don’t mention it.”

~~ Rich Olcott

A Shift in The Flight

On By rolcottIn Gravitational astronomy, Physics: Fundamentals, Physics: Newton and Gravity, UncategorizedLeave a comment

I heard a familiar squeak from the floorboard outside my office.

“C’mon in, Vinnie, the door’s open.  What can I do for you?”

“I still got problems with LIGO.  I get that dark energy and cosmic expansion got nothin’ to do with it.  But you mentioned inertial frame and what’s that about?”

earth-moon“Does the Moon go around the Earth or does the Earth go around the Moon?”

“Huh?  Depends on where you are, I guess.”

“Well, there you are.”

“Waitaminnit!  That can’t be all there is to it!”

“You’re right, there’s more.  It all goes back to Newton’s First Law.”  (showing him my laptop screen)  “Here’s how Wikipedia puts it in modern terms…”

In an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.

“That’s really a definition rather than a Law.  If you’re looking at an object and it doesn’t move relative to you or else it’s moving at constant speed in a straight line, then you and the object share the same inertial frame.  If it changes speed or direction relative to you, then it’s in a different inertial frame from yours and Newton’s Laws say that there must be some force that accounts for the difference.”

“So another guy’s plane flying straight and level with me has a piece of my inertial frame?”

“Yep, even if you’re on different vectors.  You only lose that linkage if either airplane accelerates or curves off.”

“So how’s that apply to LIGO’s laser beams?  I thought light always traveled in straight lines.”

“It does, but what’s a straight line?”

“Shortest distance between two points — I been to flight school, Sy.”

“Fine.  So if you fly from London to Mexico City on this globe here you’d drill through the Earth?”mex-atl-jfk-lgw

“Of course not, I’d take the Great Circle route that goes through those two cities.  It’s the shortest flight path.  Hey, how ’bout that, the circle goes through NYC and Atlanta, too.”

“Cool observation, but that line looks like a curve from where I sit.”

“Yeah, but you’re not sittin’ close to the globe’s surface.  I gotta fly in the flight space I got.”

“So does light.  Photons always take the shortest available path, though sometimes that path looks like a curve unless you’re on it, too.  Einstein predicted that starlight passing through the Sun’s gravitational field would be bent into a curve.  Three years later, Eddington confirmed that prediction.”

“Light doesn’t travel in a straight line?”

“It certainly does — light’s path defines what is a straight line in the space the light is traveling through.  Same as your plane’s flight path defines that Great Circle route.  A gravitational field distorts the space surrounding it and light obeys the distortion.”

“You’re getting to that ‘inertial frames’ stuff, aren’t you?”

“Yeah, I think we’re ready for it.  You and that other pilot are flying steady-speed paths along two navigation beams, OK?”

“Navigation beams are radio-frequency.”

“Sure they are, but radio’s just low-frequency light.  Stay with me.  So the two of you are zinging along in the same inertial frame but suddenly a strong gravitational field cuts across just your beam and bends it.  You keep on your beam, right?”

“I suppose so.”

“And now you’re on a different course than the other plane.  What happened to your inertial frame?”

“It also broke away from the other guy’s.”

“Because you suddenly got selfish?”

“No, ’cause my beam curved ’cause the gravity field bent it.”

“Do the radio photons think they’re traveling a bent path?”

“Uh, no, they’re traveling in a straight line in a bent space.”

“Does that space look bent to you?”

“Well, I certainly changed course away from the other pilot’s.”

“Ah, but that’s referring to his inertial frame or the Earth’s, not yours.  Your inertial frame is determined by how those photons fly, right?  In terms of your frame, did you peel away or stay on-beam?”

“OK, so I’m on-beam, following a straight path in a space that looks bent to someone using a different inertial frame.  Is that it?”

“You got it.”

(sounds of departing footsteps and closing door)

“Don’t mention it.”

~~ Rich Olcott

Breathing Space

On By rolcottIn Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Fundamentals, Physics: Newton and Gravity, UncategorizedLeave a comment

It was December, it was cold, no surprise.  I unlocked my office door, stepped in and there was Vinnie, standing at the window.  He turned to me, shrugged a little and said, “Morning, Sy.”  That’s Vinnie for you.

“Morning, Vinnie.  What got you onto the streets this early?”

“I ain’t on the streets, I’m up here where it’s warm and you can answer my LIGO question.”

“And what’s that?”

“I read your post about gravitational waves, how they stretch and compress space.  What the heck does that even mean?”

gravwave
An array of coordinate systems
floating in a zero-gravity environment,
each depicting a local x, y, and z axis

“Funny thing, I just saw a paper by Professor Saulson at Syracuse that does a nice job on that.  Imagine a boxful of something real light but sparkly, like shiny dust grains.  If there’s no gravitational field nearby you can arrange rows of those grains in a nice, neat cubical array out there in empty space.  Put ’em, oh, exactly a mile apart in the x, y, and z directions.  They’re going to serve as markers for the coordinate system, OK?”

“I suppose.”

“Now it’s important that these grains are in free-fall, not connected to each other and too light to attract each other but all in the same inertial frame.  The whole array may be standing still in the Universe, whatever that means, or it could be heading somewhere at a steady speed, but it’s not accelerating in whole or in part.  If you shine a ray of light along any row, you’ll see every grain in that row and they’ll all look like they’re standing still, right?”

“I suppose.”

“OK, now a gravitational wave passes by.  You remember how they operate?”

“Yeah, but remind me.”

(sigh)  “Gravity can act in two ways.  The gravitational attraction that Newton identified acts along the line connecting the two objects acting on each other.  That longitudinal force doesn’t vary with time unless the object masses change or their distance changes.  We good so far?”
long-and-transverse-grav
“Sure.”

“Gravity can also act transverse to that line under certain circumstances.  Suppose we here on Earth observe two black holes orbiting each other.  The line I’m talking about is the one that runs from us to the center of their orbit.  As each black hole circles that center, its gravitational field moves along with it.  The net effect is that the combined gravitational field varies perpendicular to our line of sight.  Make sense?”

“Gimme a sec…  OK, I can see that.  So now what?”

“So now that variation also gets transmitted to us in the gravitational wave.  We can ignore longitudinal compression and stretching along our sight line.  The black holes are so far away from us that if we plug the distance variation into Newton’s F=m1m2/r² equation the force variation is way too small to measure with current technology.

“The good news is that we can measure the off-axis variation because of the shape of the wave’s off-axis component.  It doesn’t move space up-and-down.  Instead, it compresses in one direction while it stretches perpendicular to that, and then the actions reverse.  For instance, if the wave is traveling along the z-axis, we’d see stretching follow compression along the x-axis at the same time as we’d see compression following stretching along the y-axis.”

gravwave-2“Squeeze in two sides, pop out the other two, eh?”

“Exactly.  You can see how that affects our grain array in this video I just happen to have cued up.  See how the up-down and left-right coordinates close in and spread out separately as the wave passes by?”

“Does this have anything to do with that ‘expansion of the Universe’ thing?”

“Well, the gravitational waves don’t, so far as we know, but the notion of expanding the distance between coordinate markers is exactly what we think is going on with that phenomenon.  It’s not like putting more frosting on the outside of a cake, it’s squirting more filling between the layers.  That cosmological pressure we discussed puts more distance between the markers we call galaxies.”

“Um-hmm.  Stay warm.”

(sound of departing footsteps and door closing)

“Don’t mention it.”

~~ Rich Olcott

Gentle pressure in the dark

On By rolcottIn Cosmology, Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Newton and Gravity, UncategorizedLeave a comment

“C’mon in, the door’s open.”

Vinnie clomps in and he opens the conversation with, “I don’t believe that stuff you wrote about LIGO.  It can’t possibly work the way they say.”

“Well, sir, would you mind telling me why you have a problem with those posts?”  I’m being real polite, because Vinnie’s a smart guy and reads books.  Besides, he’s Vinnie.

“I’m good with your story about how Michelson’s interferometer worked and why there’s no æther.  Makes sense, how the waves mess up when they’re outta step.  Like my platoon had to walk funny when we crossed a bridge.  But the gravity wave thing makes no sense.  When a wave goes by maybe it fiddles space but it can’t change where the LIGO mirrors are.”

“Gravitational wave,” I murmur, but speak up with, “What makes you think that space can move but not the mirrors?”

“I seen how dark energy spreads galaxies apart but they don’t get any bigger.  Same thing must happen in the LIGO machine.”

“Not the same, Vinnie.  I’ll show you the numbers.”

“Ah, geez, don’t do calculus at me.”de-vs-gravity

“No, just arithmetic we can do on a spreadsheet.” I fire up the laptop and start poking in  astronomical (both senses) numbers.  “Suppose we compare what happens when two galaxies face each other in intergalactic space, with what happens when two stars face each other inside a galaxy.  The Milky Way’s my favorite galaxy and the Sun’s my favorite star.  Can we work with those?”

“Yeah, why not?”

“OK, we’ll need a couple of mass numbers.  The Sun’s mass is… (sound of keys clicking as I query Wikipedia) … 2×1030 kilograms, and the Milky Way has (more key clicks) about 1012 stars.  Let’s pretend they’re all the Sun’s size so the galaxy’s mass is (2×1030)×1012 = 2×1042 kg. Cute how that works, multiplying numbers by adding exponents, eh?”

“Cute, yeah, cute.”  He’s getting a little impatient.

“Next step is the sizes.  The Milky Way’s radius is 10×104 lightyears, give or take..  At 1016 meters per lightyear, we can say it’s got a radius of 5×1020 meters.  You remember the formula for the area of a circle?”

“Sure, it’s πr2.” I told you Vinnie’s smart.

“Right, so the Milky Way’s area is 25π×1040 m2.  Meanwhile, the Sun’s radius is 1.4×109 m and its cross-sectional area must be 2π×1018 m2.  Are you with me?”

“Yeah, but what’re we doing playing with areas?  Newton’s gravity equations just talk about distances between centers.”  I told you Vinnie’s smart.

“OK, we’ll do gravity first.  Suppose we’ve got our Milky Way facing another Milky Way an average inter-galactic distance away.  That’s about 60 galaxy radii,  about 300×1020 meters.  The average distance between stars in the Milky Way is about 4 lightyears or 4×1016 meters.  (I can see he’s hooked so I take a risk)  You’re so smart, what’s that Newton equation?”

“Force or potential energy?”

“Alright, I’m impressed.  Let’s go for force.”

“Force equals Newton’s G times the product of the masses divided by the square of the distance.”

“Full credit, Vinnie.  G is about 7×10-11 newton-meter²/kilogram², so we’ve got a gravity force of (typing rapidly) (7×10-11)×(2×1042)×(2×1042)/(300×1020)² = 3.1×1029 N for the galaxies, and (7×10-11)×(2×1030)×(2×1030)/(4×1016)² = 1.75×1017 N for the stars.  Capeesh?”

“Yeah, yeah.  Get on with it.”

“Now for dark energy.  We don’t know what it is, but theory says it somehow exerts a steady pressure that pushes everything away from everything.  That outward pressure’s exerted here in the office, out in space, everywhere.  Pressure is force per unit area, which is why we calculated areas.

“But the pressure’s really, really weak.  Last I saw, the estimate’s on the order of 10-9 N/m².  So our Milky Way is pushed away from that other one by a force of (10-9)×(25π×1040) ≈ 1031 N, and our Sun is pushed away from that other star by a force of (10-9)×(2π×1018) ≈ 1010 N with rounding.  Here, look at the spreadsheet summary…”

 Force, newtons Between Galaxies Between stars
Gravity 3.1×1029 1.75×1017
Dark energy 1031 1010
Ratio 3.1×10-2 17.5×106

“So gravity’s force pulling stars together is 18 million times stronger than dark energy’s pressure pushing them apart.  That’s why the galaxies aren’t expanding.”

“Gotta go.”

(sound of door-slam )

“Don’t mention it.”

~~ Rich Olcott

Gettin’ kinky in space

On By rolcottIn Astronomy: Planetary Science, Astronomy: Stellar Science, Physics: Newton and Gravity, UncategorizedLeave a comment

Things were simpler in the pre-Enlightenment days when we only five planets to keep track of.  But Haley realized that comets could have orbits, Herschel discovered Uranus, and Galle (with Le Verrier’s guidance) found Neptune.  Then a host of other astronomers detected Ceres and a host of other asteroids, and Tombaugh observed Pluto in 1930.whirlpool-44x100-reversed

Astronomers relished the proliferation — every new-found object up there was a new test case for challenging one or another competing theory.

Here’s the currently accepted narrative…  Long ago but quite close-by, there was a cloud of dust in the Milky Way galaxy.  Random motion within it produced a swirl that grew into a vortex dozens of lightyears long.

Consider one dust particle (we’ll call it Isaac) afloat in a slice perpendicular to the vortex.  Assume for the moment that the vortex is perfectly straight, the dust is evenly spread across it, and all particles have the same mass.  Isaac is subject to two influences — gravitational and rotational.

making-a-solar-nebula
A kinked galactic cloud vortex,
out of balance and giving rise
to a solar system.

Gravity pulls Isaac towards towards every other particle in the slice.  Except for very near the slice’s center there are generally more particles (and thus more mass) toward and beyond the center than back toward the edge behind him.  Furthermore, there will generally be as many particles to Isaac’s left as to his right.  Gravity’s net effect is to pull Isaac toward the vortex center.

But the vortex spins.  Isaac and his cohorts have angular momentum, which is like straight-line momentum except you’re rotating about a center.  Both of them are conserved quantities — you can only get rid of either kind of momentum by passing it along to something else.  Angular momentum keeps Isaac rotating within the plane of his slice.

An object’s angular momentum is its linear momentum multiplied by its distance from the center.  If Isaac drifts towards the slice’s center (radial distance decreases), either he speeds up to compensate or he transfers angular momentum to other particles by colliding with them.

But vortices are rarely perfectly straight.  Moreover, the galactic-cloud kind are generally lumpy and composed of different-sized particles.  Suppose our vortex gets kinked by passing a star or a magnetic field or even another vortex.  Between-slice gravity near the kink shifts mass kinkward and unbalances the slices to form a lump (see the diagram).  The lump’s concentrated mass in turn attracts particles from adjacent slices in a viscous cycle (pun intended).

After a while the lumpward drift depletes the whole neighborhood near the kink.  The vortex becomes host to a solar nebula, a concentrated disk of dust whirling about its center because even when you come in from a different slice, you’ve still got your angular momentum.  When gravity smacks together Isaac and a few billion other particles, the whole ball of whacks inherits the angular momentum that each of its stuck-together components had.  Any particle or planetoid that tries to make a break for it up- or down-vortex gets pulled back into the disk by gravity.

That theory does a pretty good job on the conventional Solar System — four rocky Inner Planets, four gas giant Outer Planets, plus that host of asteroids and such, all tightly held in the Plane of The Ecliptic.

How then to explain out-of-plane objects like Pluto and Eris, not to mention long-period comets with orbits at all angles?outer-orbits-1

We now know that the Solar System holds more than we used to believe.  Who’s in is still “objects whose motion is dominated by the Sun’s gravitational field,” but the Sun’s net spreads far further than we’d thought.  Astronomers now hypothesize that after its creation in the vortex, the Sun accumulated an Oort cloud — a 100-billion-mile spherical shell containing a trillion objects, pebbles to planet-sized.

At the shell’s average distance from the Sun (see how tiny Neptune’s path is in the diagram) Solar gravity is a millionth of its strength at Earth’s orbit.  The gravity of a passing star or even a conjunction of our own gas giants is enough to start an Oort-cloud object on an inward journey.

These trans-Neptunian objects are small and hard to see, but they’re revolutionizing planetary astronomy.

~~ Rich Olcott

The question Newton couldn’t answer

On By rolcottIn Physics: Black Holes and Relativity, Physics: Newton and Gravity, UncategorizedLeave a comment

250 years ago, when people were getting used to the idea that the planets circle the Sun and not the other way around, they wondered how that worked.  Isaac Newton said, “I can explain it with my Laws of Motion and my Law of Gravity.”

The first Law of Motion is that an object will move in a straight line unless acted upon by a force.  If you’re holding a ball by a string and swing the ball in a circle, the reason the ball doesn’t fly away is that the string is exerting a force on the ball.  Using Newton’s Laws, if you know the mass of the ball and the length of the string, you can calculate how fast the ball moves along that circle.

Newton said that the Solar System works the same way.  Between the Sun and each planet there’s an attractive force which he called gravity.  If you can determine three points in a planet’s orbit, you can use the Laws of Motion and the Law of Gravity to calculate the planet’s speed at any time, how close it gets to the Sun, even how much the planet weighs.

Astronomers said, “This is wonderful!  We can calculate the whole Solar System this way, but… we don’t see any strings.  How does gravity work?”

Newton was an honest man.  His response was, “I don’t know how gravity works.  But I can calculate it and that should be good enough.”

And that was good enough for 250 years until Albert Einstein produced his Theories of Relativity.  This graphic shows one model of Einstein’s model of “the fabric of space.”  According to the theory, light (the yellow threads) travels at 186,000 miles per second everywhere in the Universe.

Fabric of Space 4a

As we’ve seen, the theory also says that space is curved and compressed near a massive object.  Accordingly, the model’s threads are drawn together near the dark circle, which could represent a planet or a star or a black hole.  If you were standing next to a black hole (but not too close). you’d feel fine because all your atoms and the air you breathe would shrink to the same scale.  You’d just notice through your telescope that planetary orbits and other things in the Universe appear larger than you expect.FoS wave

This video shows how a massive object’s space compression affects a passing light wave.  The brown dot and the blue dot both travel at 186,000 miles per second, but “miles are shorter near a black hole.”  The wave’s forward motion is deflected around the object because the blue dot’s miles are longer than the miles traveled by the brown dot.

When Einstein presented his General Theory of Relativity in 1916, his calculations led him to predict that this effect would cause a star’s apparent position to be altered by the Sun’s gravitational field. Fabric of Space 4b

An observer at the bottom of this diagram can pinpoint the position of star by following its light ray back to the star’s location.  Star , however, is so situated that its light ray is bent by our massive object.  To the observer, star ’s apparent position is shifted away from its true position.

In 1919, English physicist-astronomer Arthur Eddington led an expedition to the South Atlantic to test Einstein’s prediction.  Why the South Atlantic?  To observe the total eclipse of the sun that would occur there.  With the Sun’s light blocked by the Moon, Eddington would be able to photograph the constellation Taurus behind the Sun.

Sure enough, in Eddington’s photographs the stars closest to the Sun were shifted in their apparent position relative to those further way.  Furthermore, the sizes of the shifts were almost embarrassingly close to Einstein’s predicted values.

Eddington presented his photographs to a scientific conference in Cambridge and thus produced the first public confirmation of Einstein’s theory of gravity.

Wait, how does an object bending a light ray connect with that object’s pull on another mass?  Another piece of Einstein’s theory says that if a light ray and a freely falling mass both start from the same point in spacetime, both will follow the same path through space.  American physicist John Archibald Wheeler said, “Mass bends space, and bent space tells mass how to move.”

 

~~ Rich Olcott

Gravity and other fictitious forces

On By rolcottIn Physics: Fundamentals, Physics: Newton and Gravity, Uncategorized3 Comments

In this post I wrote, “gravitational force is how we we perceive spatial curvature.”
Here’s another claim — “Gravity is like centrifugal force, because they’re both fictitious.”   Outrageous, right?  I mean, I can feel gravity pulling down on me now.  How can it be fictional?

Fictitious triangle
A fictitious triangle

“Fictitious,” not “fictional,” and there’s a difference.  “Fictional” doesn’t exist, but a fictitious force is one that, to put it non-technically, depends on how you look at it.

Newton started it, of course.  From our 21st Century perspective, it’s hard to recognize the ground-breaking impact of his equation F=m·a.  Actually, it’s less a discovery than a set of definitions.  Its only term that can be measured directly is a, the acceleration, which Newton defined as any change from rest or constant-speed straight-line motion.  For instance, car buffs know that if a vehicle covers a one-mile half-mile (see comments) track in 60 seconds from a standing start, then its final speed is 60 mph (“zero to sixty in sixty”).  Furthermore, we can calculate that it achieved a sustained acceleration of 1.47 ft/sec2.

Both F and m, force and mass, were essentially invented by Newton and they’re defined in terms of each other.  Short of counting atoms (which Newton didn’t know about), the only routes to measuring a mass boil down to

  • compare it to another mass (for instance, in a two-pan balance), or
  • quantify how its motion is influenced by a known amount of force.

Conversely, we evaluate a force by comparing it to a known force or by measuring its effect on a known mass.

Once the F=m·a. equation was on the table, whenever a physicist noticed an acceleration they were duty-bound to look for the corresponding force.  An arrow leaps from the bow?  Force stored as tension in the bowstring.  A lodestone deflects a compass needle?  Magnetic force.  Objects accelerate as they fall?  Newton identified that force, called it “gravity,” and showed how to calculate it and how to apply it to planets as well as apples.  It was Newton who pointed out that weight is a measure of gravity’s force on a given mass.

Incidentally, to this day the least accurately known physical constant is Newton’s G, the Universal Gravitational Constant in his equation F=G·m1·m2/r2.  We can “weigh” planets with respect to each other and to the Sun, but without an independently-determined accurate mass for some body in the Solar System we can only estimate G.  We’ll have a better value when we can see how much rocket fuel it takes to push an asteroid around.

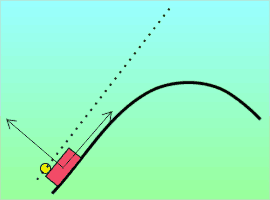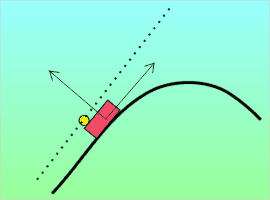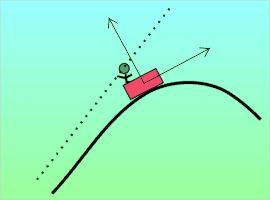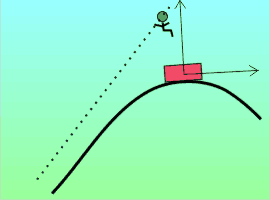CoasterBut there are other accelerations that aren’t so easily accounted for.  Ever ride in a car going around a curve and find yourself almost flung out of your seat?  This little guy wasn’t wearing his seat belt and look what happened.  The car accelerated because changing direction is an acceleration due to a lateral force.  But the guy followed Newton’s First Law and just kept going in a straight line.  Did he accelerate?

This is one of those “depends on how you look at it” cases.  From a frame of reference locked to the car (arrows), he was accelerated outwards by a centrifugal force that wasn’t countered by centripetal force from his seat belt.  However, from an earthbound frame of reference he flew in a straight line and experienced no force at all.

Side forceSuppose you’re investigating an object’s motion that appears to arise from a new force you’d like to dub “heterofugal.”  If you can find a different frame of reference (one not attached to the object) or otherwise explain the motion without invoking the “new force,” then heterofugalism is a fictitious force.

Centrifugal and centripetal forces are fictitious.  The  “force” “accelerating” one plane towards another as they both fly to the North Pole in this tale is actually geometrical and thus also fictitious   So is gravity.

In this post you’ll find a demonstration of gravity’s effect on the space around it.  Just as a sphere’s meridians give the effect of a fictitious lateral force as they draw together near its poles, the compressive curvature of space near a mass gives the effect of a force drawing other masses inward.

~~ Rich Olcott

What’s that funnel about, really?

On By rolcottIn Physics: Newton and Gravity, UncategorizedLeave a comment

If you’ve ever watched or read a space opera (oh yes, you have), you know about the gravity well that a spacecraft has to climb out of when leaving a planet.  Every time I see the Museum’s gravity well model (photo below), I’m reminded of all the answers the guy gave to, “Johnny, what can you make of this?”

The model’s a great visitor-attracter with those “planets” whizzing around the “Sun,” but this one exhibit really represents several distinct concepts.   For some of them it’s not quite the right shape.DMNS gravity well

The simplest concept is geometrical.  “Down” is the direction you move when gravity’s pulling on you.

HS cone
Gravitational potential energy change
for small height differences

A gravity well model for that concept would be just a straight line between you and the neighborhood’s most intense gravity source.

You learned the second concept in high school physics class.  Any object has gravitational potential energy that measures the amount of energy it would give up on falling.  Your teacher probably showed you the equation GPE = m·g·h, where m is the mass of the object, h is its height above ground level, and g is a constant you may have determined in a lab experiment.

If the width of the gravity well model at a given height represents GPE at that level, the model is a simple straight-sided cone.

Newton energy cone
Gravitational potential energy change
for large height differences
The h indicates
an approximately linear range
where the HS equation could apply.

But of course it’s not that simple.  Newton’s Law of Gravity says that the potential energy at any height r away from the planet’s center is proportional to 1/r.

Hmm… that looks different from the “proportional to h” equation.  Which is right?

Both equations are valid, but over different distance scales.  The HS teachers didn’t quite lie to you, but they didn’t give you the complete picture either.  Your classroom was about 4000 miles (21,120,000 feet) from Earth’s center, whereas the usual experiments involve height differences of at most a dozen feet.  Even the 20-foot drop from a second-story window is less than a millionth of the way down to Earth’s center.

Check my numbers:

Height h 1/(r+h)
× 108		 Difference in 1/(r+h)
× 1014
0 4.734,848,484 0
20 4.734,844,001 4.48
40 4.734,839,517 8.97
60 4.734,835,033 13.45
80 4.734,830,549 17.93
100 4.734,826,066 22.42

rh lineSure enough, that’s a straight line (see the chart).  Reminds me of how Newton’s Law of Gravity is valid except at very short distances.  The HS Law of Gravity works fine for small spans but when the distances get big we have to use Newton’s equation.

We’re not done yet. That curvy funnel-shaped gravity well model could represent the force of gravity rather than its potential energy.  Newton told us that the force goes as 1/r2 so it decreases much more rapidly than the potential energy does as you get further away.  The gravity force well has a correspondingly sharper curve to it than the gravity energy well.

Newton force cone
The force of gravity
or an embedding diagram

The funnel model could also represent the total energy required to get a real spacecraft off the surface and up into space.  Depending on which sci-fi gimmickry is in play, the energy may come from a chemical or ion rocket, an electromagnetic railgun, or even a tractor beam from some mothership way up there.

No matter the technology, the theoretical energy requirement to get to a given height is the same.  In practice, however, each technology is optimal for some situations but forbiddingly inefficient in others.  Thus, each technology’s funnel  has its own shape and that shape will change depending on the setting.

In modern physics, the funnel model could also represent Einstein’s theory of how a mass “bends” the space around it.  (Take a look at this post, which is about how mass curves space by changing the local distance scale.)  Cosmologists describe the resulting “shapes” with embedding diagrams that are essentially 2D pictures of 3D (or 4D) contour plots.  The contours are closest together where space is most compressed, just as lines showing a steep hillside on a landscape contour map are close together.

The ED around a non-spinning object looks just like the force model picture above.  No surprise — gravitational force is how we we perceive spatial curvature.

~~ Rich Olcott

Gargh, His Heirs, and the AAAD Problem

On By rolcottIn Physics: Fundamentals, Physics: Newton and Gravity, UncategorizedLeave a comment

Gargh the thinkerGargh, proto-humanity’s foremost physicist 2.5 million years ago, opened a practical investigation into how motion works.  “I throw rock, hit food beast, beast fall down yes.  Beast stay down no.  Need better rock.”  For the next couple million years, we put quite a lot of effort into making better rocks and better ways to throw them.  Less effort went into understanding throwing.

There seemed to be two kinds of motion.  The easier kind to understand was direct contact — “I push rock, rock move yes.  Rock stop move when rock hit thing that move no.”  The harder kind was when there wasn’t direct contact — “I throw rock up, rock hit thing no but come back down.  Why that?”

Gargh was the first but hardly the last physicist to puzzle over the Action-At-A-Distance problem (a.k.a. “AAAD”).  Intuition tells us that between pusher and pushee there must be a concrete linkage to convey the push-force.  To some extent, the history of physics can be read as a succession of solutions to the question, “What linkage induces this apparent case of AAAD?”

Most of humanity was perfectly content with AAAD in the form of magic of various sorts.  To make something happen you had to wish really hard and/or depend on the good will of some (generally capricious) elemental being.

aristotle 1Aristotle wasn’t satisfied with anything so unsystematic.  He was just full of theories, many of which got in each other’s way.  One theory was that things want to go where they’re comfortable  because of what they’re made of — stones, for instance, are made of earth so naturally they try to get back home and that’s why we see them fall downwards (no concrete linkage, so it’s still AAAD).

Unfortunately, that theory didn’t account for why a thrown rock doesn’t just fall straight down but instead goes mostly in the direction it’s thrown.  Aristotle (or one of his followers) tied that back to one of his other theories, “Nature hates a vacuum.”  As the rock flies along, it pushes the air aside (direct contact) and leaves a vacuum behind it. More air rushes in to fill the vacuum and pushes the rock ahead (more direct contact).

We got a better (though still AAAD) explanation in the 17th Century when physicists invented the notions of gravity and inertia.Newton 204

Newton made a ground-breaking claim in his Principia.  He proposed that the Solar System is held together by a mysterious AAAD force he called gravity.  When critics asked how gravity worked he shrugged, “I do not form hypotheses” (though he did form hypotheses for light and other phenomena).

Inertia is also AAAD.  Those 17th Century savants showed that inertial forces push mass towards the Equator of a rotating object.  An object that’s completely independent of the rest of the Universe has no way to “know” that it’s rotating so it ought to be a perfect sphere.  In fact, the Sun and each of its planets are wider at the equator than you’d expect from their polar diameters.  That non-sphere-ness says they must have some AAAD interaction with the rest of the Universe.  A similar argument applies to linear motion; the general case is called Mach’s Principle.
JCMaxwell

The ancients knew of the mysterious AAAD agents electricity and its fraternal twin, magnetism.  However, in the 19th Century James Clerk Maxwell devised a work-around.  Just as Newton “invented” gravity, Maxwell “invented” the electromagnetic field.  This invisible field isn’t a material object.  However, waves in the field transmit electromagnetic forces everywhere in the Universe.  Not AAAD, sort of.

It wasn’t long before someone said, “Hey, we can calculate gravity that way, too.”  That’s why we now speak of a planet’s gravitational field and gravitational waves.

But the fields still felt like AAAD because they’re not concrete.  Some modern physicists stand that objection on its head.  Concrete objects, they say, are made of atoms which themselves are nothing more than persistent fluctuations in the electromagnetic and gravitational fields.  By that logic, the fields are what’s fundamental — all motion is by direct contact.einstein-tongue edged

Einstein moved resolutely in both directions.  He negated gravity’s AAAD-ness by identifying mass-contorted space as the missing linkage.  On the other hand, he “invented” quantum entanglement, the ultimate spooky AAAD.

 ~~ Rich Olcott

How rockets don’t work

On By rolcottIn General: Fun Stuff, Physics: Fundamentals, Physics: Newton and GravityLeave a comment

WoodyI was only 10 years old but already had Space Fever thanks to Chesley Bonestell’s artwork in Collier’s and Life magazines.  I eagerly joined the the movie theater ticket line to see George Pal’s Destination Moon.  I loved the Woody Woodpecker cartoon (it’s 12 minutes into the YouTube video) that explained rockets to a public just getting used to jet planes.  But the explanation’s wrong.

Go ahead, follow the link and watch the cartoon.  I’ll wait here.

Pretty far-sighted for 1950, eh?  And it’s amazing how much they got right, including how the driving force for the Space Race was international politics.  But oh, the physics…

Yeah, they tacitly acknowledged Newton’s Third Law: For every action there is an equal and opposite reaction.  The cartoon implies that the action is the pellets coming out of the barrel and the reaction is Woody getting knocked back.  But that can’t be right: if it were true you wouldn’t get any kick when you fire a blank cartridge — but you do.  Let’s take a close look at just what actions are in play.

Maybe it’s the pellets plus the gases behind it pushing forward and the gun pushing backward?  Sort of, but where do the gases come from?  Right, the exploding charge next to your cheek in the receiver.  Those gases move equally in all directions.  Some of them push pellets down the barrel.  Some of them push on the back end of the receiver which pushes the gun stock which mashes your shoulder.  But there’s bunches of molecules that uselessly collide with the receiver’s walls.

Action and reaction balance out just fine but only when you consider the gases moving outward from the center of the BANG.  For instance, if left and right didn’t balance perfectly the piece would crash into your ear or swing around and flatten your nose or the back of your head.

Both shotguns and conventional rockets get their propulsive energy from chemical combustion.  The reason gun parts have to be strong is all those hot molecules dashing in every direction other than down and up the barrel.  A chemical rocket casing has to be strong for the same reason.

Chemical combustion is just not an efficient use of propellant mass.  Just look at this NASA image of a SpaceX Falcon 9 during a DSCOVR launch — huge side-flare from molecules that make no contribution to forward thrust:DSCOVR launch
Wouldn’t it be nice if we had a way to put all our propulsion energy into moving the vehicle forward?

There’s good news and not-so-good news.  People are working on a few other options, all of which depend on forces we know how to steer: electric and magnetic.  Unfortunately, each of them has drawbacks.

Unlike rockets, ion thrusters use an electric or magnetic field to accelerate ions (duh!) away from the vehicle.  It’s a much more efficient process because there’s little off-axis action/reaction — all the propellant heads out the nozzle (action) and all the push-back force (reaction) acts directly on the vehicle.

But… ions resist being crowded together so you can’t blast huge quantities out the nozzle like you’d need to for a launch from Earth.  Up in space, though, ion thrusters are perfect for satellite attitude adjustment and similar low-power tasks.  The Dawn mission to Vesta and Ceres used an ion thruster to boost the spacecraft continuously from Earth to target.  It’d be impractical to build a chemical-powered system to do that.

Rather than send out atoms one by one, a rail-gun drive could use high-power magnetic fields to accelerate lumps of iron down a track and away.  Iron goes one way, vessel goes the other.  Might work in the Asteroid Belt where lumps of iron are there by the billions, but on the other hand I’d rather not be a Belter tooling along in my mining tug only to be hit amidships by someone’s cast-off reaction mass.

And then there’s the Q-thruster and EmDrive.  I hope to eventually include enough physics background in this blog that we can discuss the controversies and prospects for new-physics drives based on space warps and such.  You can check out Dr Harold White’s video for some of that.  It’d be sooo cool if they work.

~~ Rich Olcott