Tag: Force

Hiding Under Many Guises

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized3 Comments

Vinnie lifts his pizza slice and pauses. “I dunno, Sy, this Pressure‑Volume part of enthalpy, how is it energy so you can just add or subtract it from the thermal and chemical kinds?”

“Fair question, Vinnie. It stumped scientists through the end of Napoleon’s day until Sadi Carnot bridged the gap by inventing thermodynamics.”

“Sounds like a big deal from the way you said that.”

“Oh, it was. But first let’s clear the ‘is it energy?’ question. How would Newton have calculated the work you did lifting that slice?”

“How much force I used times the distance it moved.”

“Putting units to that, it’d be force in newtons times distance in meters. A newton is one kilogram accelerated by one meter per second each second so your force‑distance work there is measured in kilograms times meters‑squared divided by seconds‑squared. With me?”

“Hold on — ‘per second each second’ turned into ‘per second‑squared.” <pause> “Okay, go on.”

“What’s Einstein’s famous equation?”

“Easy, E=mc².”

“Mm-hm. Putting units to that, c is in meters per second, so energy is kilograms times meters‑squared divided by seconds‑squared. Sound familiar?”

“Any time I’ve got that combination I’ve got energy?”

“Mostly. Here’s another example — a piston under pressure. Pressure is force per unit area. The piston’s area is in square meters so the force it feels is newtons per meter‑squared, times square meters, or just newtons. The piston travels some distance so you’ve got newtons times meters.”

“That’s force‑distance work units so it’s energy, too.”

“Right. Now break it down another way. When the piston travels that distance, the piston’s area sweeps through a volume measured in meters‑cubed, right?”

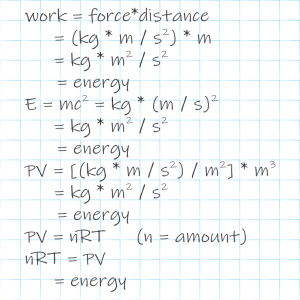
“You’re gonna say pressure times volume gives me the same units as energy?”

“Work it out. Here’s a paper napkin.”

“Dang, I hate equations … Hey, sure enough, it boils down to kilograms times meters‑squared divided by seconds‑squared again!”

“There you go. One more. The Ideal Gas Law is real simple equation —”

“Gaah, equations!”

“Bear with me, it’s just PV=nRT.”

“Is that the same PV so it’s energy again?”

“Sure is. The n measures the amount of some gas, could be in grams or whatever. The R, called the Gas Constant, is there to make the units come out right. T‘s the absolute temperature. Point is, this equation gives us the basis for enthalpy’s chemical+PV+thermal arithmetic.”

“And that’s where this Carnot guy comes in.”

“Carnot and a host of other physicists. Boyle, Gay‑Lussac, Avagadro and others contributed to Clapeyron’s gas law. Carnot’s 1824 book tied the gas narrative to the energetics narrative that Descartes, Leibniz, Newton and such had been working on. Carnot did it with an Einstein‑style thought experiment — an imaginary perfect engine.”

“Anything perfect is imaginary, I know that much. How’s it supposed to work?”

<sketching on another paper napkin> “Here’s the general idea. There’s a sealed cylinder in the middle containing a piston that can move vertically. Above the piston there’s what Carnot called ‘a working body,’ which could be anything that expands and contracts with temperature.”

“Steam, huh?”

“Could be, or alcohol vapor or a big lump of iron, whatever. Carnot’s argument was so general that the composition doesn’t matter. Below the piston there’s a mechanism to transfer power from or to the piston. Then we’ve got a heat source and a heat sink, each of which can be connected to the cylinder or not.”

“Looks straight‑forward.”

“These days, sure. Not in 1824. Carnot’s gadget operates in four phases. In generator mode the working body starts in a contracted state connected to the hot Th source. The body expands, yielding PV energy. In phase 2, the body continues to expand while it while it stays at Th. Phase 3, switch to the cold Tc heat sink. That cools the body so it contracts and absorbs PV energy. Phase 4 compresses the body to heat it back to Th, completing the cycle.”

“How did he keep the phases separate?”

“Only conceptually. In real life Phases 1 and 2 would occur simultaneously. Carnot’s crucial contribution was to treat them separately and yet demonstrate how they’re related. Unfortunately, he died of scarlet fever before Clapeyron and Clausius publicized and completed his work.”

~ Rich Olcott

Two Against One, And It’s Not Even Close

On By rolcottIn Astronomy: Planetary Science, UncategorizedLeave a comment

On a brisk walk across campus when I hear Vinnie yell from Al’s coffee shop. “Hey! Sy! Me and Al got this argument going you gotta settle.”

“Happy to be a peacemaker, but it’ll cost you a mug of Al’s coffee and a strawberry scone.”

“Coffee’s no charge, Sy, but the scone goes on Vinnie’s tab. What’s your pleasure?”

“It’s morning, Al, time for black mud. What’s the argument, Vinnie?”

“Al read in one of his astronomy magazines that the Moon’s drifting away from us. Is that true, and if it is, how’s it happen? Al thinks Jupiter’s gravity’s lifting it but I think it’s because of Solar winds pushing it. So which is it?”

“Here you go, Sy, straight from the bottom of the pot.”

“Perfect, Al, thanks. Yes, it’s true. The drift rate is about 1¼ nanometers per second, 1½ inches per year. As to your argument, you’re both wrong.”

“Huh?”
 ”Aw, c’mon!”

“Al, let’s put some numbers to your hypothesis. <pulling out Old Reliable and screen‑tapping> I’m going to compare Jupiter’s pull on the Moon to Earth’s when the two planets are closest together. OK?”

“I suppose.”

“Alright. Newton’s Law tells us the pull is proportional to the mass. Jupiter’s mass is about 320 times Earth, which is pretty impressive, right? But the attraction drops with the square of the distance. The Moon is 1¼ lightseconds from Earth. At closest approach, Jupiter is almost 2100 lightseconds away, 1680 times further than the Moon. We need to divide the 320 mass factor by a 1680‑squared distance factor and that makes <key taps> Jupiter’s pull on the Moon is only 0.011 percent of Earth’s. It’ll be <taps> half that when Jupiter’s on the other side of the Sun. Not much competition, eh?”

“Yeah, but a little bit at a time, it adds up.”

“We’re not done yet. The Moon feels the big guy’s pull on both sides of its orbit around Earth. On the side where the Moon’s moving away from Jupiter, you’re right, Jupiter’s gravity slows the Moon down, a little. But on the moving-toward-Jupiter side, the motion’s sped up. Put it all together, Jupiter’s teeny pull cancels itself out over every month’s orbiting.”

“Gotcha, Al. So what about my theory, Sy?”

“Basically the same logic, Vinnie. The Solar wind varies, thanks to the Sun’s variable activity, but satellite measurements put its pressure somewhere around a nanopascal, a nanonewton per square meter. Multiply that by the Moon’s cross‑sectional area and we get <tap, tap> a bit less than ten thousand newtons of force on the Moon. Meanwhile, Newton’s Law says the Earth’s pull on the Moon comes to <tapping>
  G×(Earth’s mass)×(Moon’s mass)/(Earth-Moon distance)²
and that comes to 2×1011 newtons. Earth wins by a 107‑fold landslide. Anyway, the pressure slows the Moon for only half of each month and speeds it up the other half so we’ve got another cancellation going on.”

“So what is it then?”
 ”So what is it then?”

“Tides. Not just ocean tides, rock tides in Earth’s fluid outer mantle. Earth bulges, just a bit, toward the Moon. But Earth also rotates, so the bulge circles the planet every day.”

“Reminds me of the wave in the Interstellar movie, but why don’t we see it?”

“The movie’s wave was hundreds of times higher than ours, Al. It was water, not rock, and the wave‑raiser was a huge black hole close by the planet. The Moon’s tidal pull on Earth produces only a one‑meter variation on a 6,400,000‑meter radius. Not a big deal to us. Of course, it makes a lot of difference to the material that’s being kneaded up and down. There’s a lot of friction in those layers.”

“Friction makes heat, Sy. Rock tides oughta heat up the planet, right?”

“Sure, Vinnie, the process does generate heat. Force times distance equals energy. Raising the Moon by 1¼ nanometers per second against a force of 2×1021 newtons gives us <taping furiously> an energy transfer rate of 4×10‑23 joules per second per kilogram of Earth’s 6×1024‑kilogram mass. It takes about a thousand joules to heat a kilogram of rock by one kelvin so we’re looking at a temperature rise near 10‑27 kelvins per second. Not significant.”

“No blaming climate change on the Moon, huh?”

~~ Rich Olcott

Conversation of Momentum

On By rolcottIn Physics: Fundamentals, Uncategorized2 Comments

Teena bounces out of the sandbox, races over to the playground’s little merry-go-round and shoves it into motion. “Come help turn this, Uncle Sy, I wanna go fast!” She leaps onto the moving wheel and of course she promptly falls off. The good news is that she rolls with the fall like I taught her to do.

“Why can’t I stay on, Uncle Sy?”

“What’s your new favorite word again?”

“Mmmo-MMENN-tumm. But that had to do with swings.”

“Swings and lots of other stuff, including merry-go-rounds and even why you should roll with the fall. Which, by the way, you did very well and I’m glad about that because we don’t want you getting hurt on the playground.”

“Well, it does hurt a little on my elbow, see?”

“Let me look … ah, no bleeding, things only bend where they’re supposed to … I think no damage done but you can ask your Mommie to kiss it if it still hurts when we get home. But you wanted to know why you fell off so let’s go back to the sandbox to figure that out.”

<scamper!> “I beat you here!”

“Of course you did. OK, let’s draw a big arc and pretend that’s looking down on part of the merry-go-round. I’ll add some lines for the spokes and handles. Now I’ll add some dots and arrows to show what I saw from over here. See, the merry-go-round is turning like this curvy arrow shows. You started at this dot and jumped onto this dot which moved along and then you fell off over here. Poor Teena. So you and your momentum mostly went left-to-right.”

“But that’s not what happened, Uncle Sy. Here, I’ll draw it. I jumped on but something tried to push me off and then I did fall off and then I rolled. Poor me. Hey, my arm doesn’t hurt any more!”

“How about that? I’ve often found that thinking about something else makes hurts go away. So what do you think was trying to push you off? I’ll give you a hint with these extra arrows on the arc.”

“That looks like Mr Newton’s new directions, the in-and-out direction and the going-around one. Oh! I fell off along the in-and-out direction! Like I was a planet and the Sun wasn’t holding me in my orbit! Is that what happened, I had out-momentum?”

“Good thinking, Teena. Mr Newton would say that you got that momentum from a force in the out-direction. He’d also say that if you want to stand steady you need all the forces around you to balance each other. What does that tell you about what you need to do to stay on the merry-go-round?”

“I need an in-direction force … Hah, that’s what I did wrong! I jumped on but I didn’t grab the handles.”

“Lesson learned. Good.”

“But what about the rolling?”

“Well, in general when you fall it’s nearly always good to roll the way your body’s spinning and only try to slow it down. People who put out an arm or leg to stop a fall often stress it and and maybe even tear or break something.”

“That’s what you’ve told me. But what made me spin?”

“One of Mr Newton’s basic principles was a rule called ‘Conservation of Momentum.’ It says that you can transfer momentum from one thing to another but you can’t create it or destroy it. There are some important exceptions but it’s a pretty good rule for the cases he studied. Your adventure was one of them. Look back at the picture I drew. You’d built up a lot of going-around momentum from pushing the merry-go-round to get it started. You still had momentum in that direction when you fell off. Sure enough, that’s the direction you rolled.”

“Is that the ‘Conversation of Energy’ thing that you and Mommie were talking about?”

“Conservation. It’s not the same but it’s closely related.”

“Why does it even work?”

“Ah, that’s such a deep question that most physicists don’t even think about it. Like gravity, Mr Newton described what inertia and momentum do, but not how they work. Einstein explained gravity, but I’m not convinced that we understand mass yet.”

~~ Rich Olcott

Gravity and other fictitious forces

On By rolcottIn Physics: Fundamentals, Physics: Newton and Gravity, Uncategorized3 Comments

In this post I wrote, “gravitational force is how we we perceive spatial curvature.”
Here’s another claim — “Gravity is like centrifugal force, because they’re both fictitious.”   Outrageous, right?  I mean, I can feel gravity pulling down on me now.  How can it be fictional?

Fictitious triangle
A fictitious triangle

“Fictitious,” not “fictional,” and there’s a difference.  “Fictional” doesn’t exist, but a fictitious force is one that, to put it non-technically, depends on how you look at it.

Newton started it, of course.  From our 21st Century perspective, it’s hard to recognize the ground-breaking impact of his equation F=m·a.  Actually, it’s less a discovery than a set of definitions.  Its only term that can be measured directly is a, the acceleration, which Newton defined as any change from rest or constant-speed straight-line motion.  For instance, car buffs know that if a vehicle covers a one-mile half-mile (see comments) track in 60 seconds from a standing start, then its final speed is 60 mph (“zero to sixty in sixty”).  Furthermore, we can calculate that it achieved a sustained acceleration of 1.47 ft/sec2.

Both F and m, force and mass, were essentially invented by Newton and they’re defined in terms of each other.  Short of counting atoms (which Newton didn’t know about), the only routes to measuring a mass boil down to

  • compare it to another mass (for instance, in a two-pan balance), or
  • quantify how its motion is influenced by a known amount of force.

Conversely, we evaluate a force by comparing it to a known force or by measuring its effect on a known mass.

Once the F=m·a. equation was on the table, whenever a physicist noticed an acceleration they were duty-bound to look for the corresponding force.  An arrow leaps from the bow?  Force stored as tension in the bowstring.  A lodestone deflects a compass needle?  Magnetic force.  Objects accelerate as they fall?  Newton identified that force, called it “gravity,” and showed how to calculate it and how to apply it to planets as well as apples.  It was Newton who pointed out that weight is a measure of gravity’s force on a given mass.

Incidentally, to this day the least accurately known physical constant is Newton’s G, the Universal Gravitational Constant in his equation F=G·m1·m2/r2.  We can “weigh” planets with respect to each other and to the Sun, but without an independently-determined accurate mass for some body in the Solar System we can only estimate G.  We’ll have a better value when we can see how much rocket fuel it takes to push an asteroid around.

CoasterBut there are other accelerations that aren’t so easily accounted for.  Ever ride in a car going around a curve and find yourself almost flung out of your seat?  This little guy wasn’t wearing his seat belt and look what happened.  The car accelerated because changing direction is an acceleration due to a lateral force.  But the guy followed Newton’s First Law and just kept going in a straight line.  Did he accelerate?

This is one of those “depends on how you look at it” cases.  From a frame of reference locked to the car (arrows), he was accelerated outwards by a centrifugal force that wasn’t countered by centripetal force from his seat belt.  However, from an earthbound frame of reference he flew in a straight line and experienced no force at all.

Side forceSuppose you’re investigating an object’s motion that appears to arise from a new force you’d like to dub “heterofugal.”  If you can find a different frame of reference (one not attached to the object) or otherwise explain the motion without invoking the “new force,” then heterofugalism is a fictitious force.

Centrifugal and centripetal forces are fictitious.  The  “force” “accelerating” one plane towards another as they both fly to the North Pole in this tale is actually geometrical and thus also fictitious   So is gravity.

In this post you’ll find a demonstration of gravity’s effect on the space around it.  Just as a sphere’s meridians give the effect of a fictitious lateral force as they draw together near its poles, the compressive curvature of space near a mass gives the effect of a force drawing other masses inward.

~~ Rich Olcott

The direction Newton avoided facing

On By rolcottIn Physics: Fundamentals, Physics: Newton and Gravity, UncategorizedLeave a comment

Reading Newton’s Philosophiæ Naturalis Principia Mathematica is less challenging than listening to Vogon poetry.  You just have to get your head working like a 17th Century genius who had just invented Calculus and who would have deep-fried his right arm in rancid skunk oil before he’d admit to using any of his rival Leibniz’ math notations or techniques.

Newton II-II ellipseNewton was essentially a geometer. These illustrations (from Book 1 of the Principia) will give you an idea of his style.  He’d set himself a problem then solve it by constructing sometimes elaborate diagrams by which he could prove that certain components were equal or in strict proportion.

Newton XII-VII hyperbolaFor instance, in the first diagram (Proposition II, Theorem II), we see an initial glimpse of his technique of successive approximation.  He defines a sequence of triangles which as they proliferate get closer and closer to the curve he wants to characterize.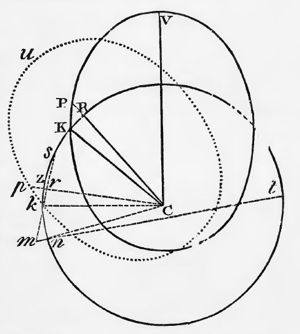

The lines and trig functions escalate in the second diagram (Prop XII, Problem VII), where he calculates the force  on a body traveling along a hyperbola.

Newton XLIV-XIV precessionThe third diagram is particularly relevant to the point I’ll finally get to when I get around to it.  In Prop XLIV, Theorem XIV he demonstrates something weird.  Suppose two objects A and B are orbiting around attractive center C, but B is moving twice as fast as A.  If C exerts an additional force on B that is inversely dependent on the cube of the B-C distance, then A‘s orbit will be a perfect circle (yawn) but B‘s will be an ellipse that rotates around C, even though no external force pushes it laterally.

In modern-day math we’d write the additional force as F∼(1/rBC3), but Newton verbalized it as “in a triplicate ratio of their common altitudes inversely.”  See what I mean about Vogon poetry?

Now, about that point I was going to get to.  It’s C, in the center of that circle.  If the force is proportional to 1/r3, what happens when r approaches zero?  BLOOIE, the force becomes infinite.

In the previous post we used geometry to understand the optical singularity at the center of the Christmas ball.  I said there that my modeling project showed me a deeper reason for a BLOOIE.  That reason showed up partway through the calculation for the angle between the axis and the ring of reflected  light.  A certain ratio came out to be (1-x)/2x, where x is proportional to the distance between the LED and the ball’s center.  Same problem: as the LED approaches the center, x approaches zero and BLOOIE.  (No problem when x is one, because the ratio is 0/2 which is zero which is OK.)

Singularities happen when the formula for something goes to infinity.

Now, Newton recognized that his central-force (1/rn)-type equations covered gravity and magnetism and even the inward force on the rim of a rotating wheel.  It’s surprising that he didn’t seem too worried about BLOOIE.

I think he had two excuses.  First, he was limited by his graphical methodology.  In most of his constructions, when a certain distance goes to zero there’s a general catastrophe — rectangles and triangles collapse to lines or even points, radii whirl aimlessly without a vertex to aim at…  His lovely derivations devolve into meaninglessness.  Further advances would depend on the  algebraic approach to Calculus taken by the detested Leibniz.

Second (here’s the hook for this post’s title), Newton was looking outward, not inward.  He was considering the orbits of planets and other sizable objects.  r is always the distance between object centers.  For sizable objects you don’t have to worry about r=0 because “center-to-center equals zero” never occurs.  If the Moon (radius 1080 miles) were to drop down to touch the Earth (radius 3960 miles), their centers would still be 5000 miles apart.  No BLOOIE.

Actually, there would be CRUMBLE instead of BLOOIE because a different physical model would apply — but that’s a tale for another post.

The moral of the story is this.  Mathematical models don’t care about infinities, but Nature does.  Any conditions where the math predicts an infinite value (for instance, where a denominator can become zero) are prime territory for new models that make better predictions.

~~ Rich Olcott

And now for some completely different dimensions

On By rolcottIn Mathematics: Dimensions, Physics: Fundamentals, UncategorizedLeave a comment

Terry Pratchett wrote that Knowledge = Power = Energy = Matter = Mass.  Physicists don’t agree because the units don’t match up.

Physicists check equations with a powerful technique called “Dimensional Analysis,” but it’s only theoretically related to the “travel in space and time” kinds of dimension we discussed earlier.

Place setting LMTIt all started with Newton’s mechanics, his study of how objects affect the motion of other objects.  His vocabulary list included words like force, momentum, velocity, acceleration, mass, …, all concepts that seem familiar to us but which Newton either originated or fundamentally re-defined. As time went on, other thinkers added more terms like power, energy and action.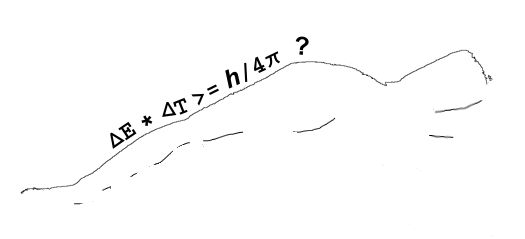

They’re all linked mathematically by various equations, but also by three fundamental dimensions: length (L), time (T) and mass (M). (There are a few others, like electric charge and temperature, that apply to problems outside of mechanics proper.)

Velocity, for example.  (Strictly speaking, velocity is speed in a particular direction but here we’re just concerned with its magnitude.)   You can measure it in miles per hour or millimeters per second or parsecs per millennium — in each case it’s length per time.  Velocity’s dimension expression is L/T no matter what units you use.

Momentum is the product of mass and velocity.  A 6,000-lb Escalade SUV doing 60 miles an hour has twice the momentum of a 3,000-lb compact car traveling at the same speed.  (Insurance companies are well aware of that fact and charge accordingly.)  In terms of dimensions, momentum is M*(L/T) = ML/T.

Acceleration is how rapidly velocity changes — a car clocked at “zero to 60 in 6 seconds” accelerated an average of 10 miles per hour per second.  Time’s in the denominator twice (who cares what the units are?), so the dimensional expression for acceleration is L/T2.

Physicists and chemists and engineers pay attention to these dimensional expressions because they have to match up across an equal sign.  Everyone knows Einstein’s equation, E = mc2. The c is the velocity of light.  As a velocity its dimension expression is L/T.  Therefore, the expression for energy must be M*(L/T)2 = ML2/T2.  See how easy?

Now things get more interesting.  Newton’s original Second Law calculated force on an object by how rapidly its momentum changed: (ML/T)/T.  Later on (possibly influenced by his feud with Leibniz about who invented calculus), he changed that to mass times acceleration M*(L/T2).  Conceptually they’re different but dimensionally they’re identical — both expressions for force work out to ML/T2.

Something seductively similar seems to apply to Heisenberg’s Area.  As we’ve seen, it’s the product of uncertainties in position (L) and momentum (ML/T) so the Area’s dimension expression works out to L*(ML/T) = ML2/T.

SeductiveThere is another way to get the same dimension expression but things aren’t not as nice there as they look at first glance.  Action is given by the amount of energy expended in a given time interval, times the length of that interval.  If you take the product of energy and time the dimensions work out as (ML2/T2)*T = ML2/T, just like Heisenberg’s Area.

It’s so tempting to think that energy and time negotiate precision like position and momentum do.  But they don’t.  In quantum mechanics, time is a driver, not a result.  If you tell me when an event happens (the t-coordinate), I can maybe calculate its energy and such.  But if you tell me the energy, I can’t give you a time when it’ll happen.  The situation reminds me of geologists trying to predict an earthquake.  They’ve got lots of statistics on tremor size distribution and can even give you average time between tremors of a certain size, but when will the next one hit?  Lord only knows.

File the detailed reasoning under “Arcane” — in technicalese, there are operators for position, momentum and energy but there’s no operator for time.  If you’re curious, John Baez’s paper has all the details.  Be warned, it contains equations!

Trust me — if you’ve spent a couple of days going through a long derivation, totting up the dimensions on either side of equations along the way is a great technique for reassuring yourself that you probably didn’t do something stupid back at hour 14.  Or maybe to detect that you did.

~~ Rich Olcott