Tag: Jupiter

A Spherical Bandstand

On By rolcottIn Astronomy: Planetary Science, Mathematics, Mathematics: Spherical Harmonics, UncategorizedLeave a comment
Radial harmonics Rn = Ln e-nr

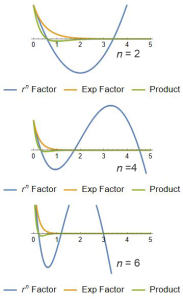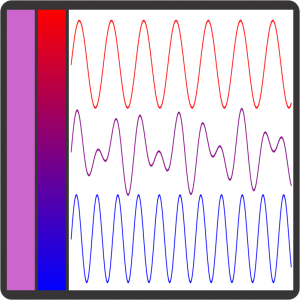
“Whoa, Sy, something’s not right. Your zonal harmonics — I can see how latitudes go from pole to pole and that’s all there are. Your sectorial harmonic longitudes start over when they get to 360°, fine. But this chart you showed us says that the radius basically disappears crazy close to zero. The radius should keep going forever, just like x, y and z do.”

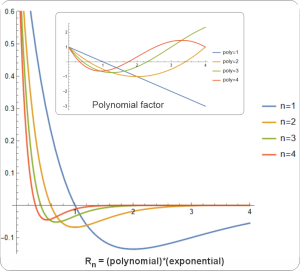
“Ah, I see the confusion, Susan. The coordinate system and the harmonic systems and the waves are three different things, um, groups of things. You can think of a coordinate system as a multilevel stage where chords of harmonic musicians can interact to play a composition of wave signals. The spherical system has latitude and longitude levels for the brass and woodwind players, plus one in back for the linear percussion section. Whichever direction the brass and woodwinds point, that’s where the signals go out, but it’s the percussion that determines how far they get. Sure, radius lines extend to infinity but except for R0 radial harmonics damp out pretty quickly.”

“Signals… Like Kaski’s team interpreted Juno‘s orbital twitches as a signal about Jupiter’s gravitational unevenness. Good thing Juno got close enough to be inside the active range for those radial harmonics. How’d they figure that?”

“They probably didn’t, Cathleen, because radial harmonics don’t fit easily into real situations. First problem is scale — what units do you measure r in? There’s an easy answer if the system you’re working with is a solid ball, not so easy if it’s blurry like a protein blob or galaxy cluster.”

“What makes a ball easy?”

“Its rigid surface that doesn’t move so it’s always a node. Useful radial harmonics must have a node there, another node at zero and an integer number of nodes between. Better yet, with the ball’s radius as a natural length unit the r coordinate runs linearly between zero at the center and 1.0 at the surface. Simplifies computation and analysis. In contrast, blurries usually don’t have convenient natural radial units so we scrabble around for derived metrics like optical depth or mixing length. If we’re forced into doing that, though, we probably have worse challenges.”

“Like what?”

“Most real-world spherical systems aren’t the same all the way through. Jupiter, for instance, has separate layers of stratosphere, troposphere, several chemically distinct cloud‑phases, down to helium raining on layers of hydrogen in liquid, maybe slushy or even solid form. Each layer has its own suite of physical properties that put kinks into a radial harmonic’s smooth curve. Same problem with the Sun.”

“How about my atoms? The whole Periodic Table is based on atoms having a shell structure. What about the energy level diagrams for atomic spectra? They show shells.”

“Well, they do and they don’t, Susan. Around the turn of the last Century, Lyman, Balmer, Paschen, Brackett and Pfund—”

“Sounds like a law firm.”

“<ironically> Ha, ha. No, they were experimental physicists who gave the theoreticians an important puzzle. Over a 40‑year period first Balmer and then the others, one series at a time, measured the wavelengths of dozens of lines in hydrogen’s spectrum. ’Okay, smarties, explain those!‘ So the theoreticians invented quantum mechanics. The first shot did a pretty good job for hydrogen. It explained the lines as transitions between discrete states with different energy levels. It then explained the energy levels in terms of charge being concentrated at different distances from the nucleus. That’s where the shell idea came from. Unfortunately, the theory ran into problems for atoms with more than one electron.”

“Give us a second… Ah, I get why. If one electron avoids a node, another one dives in there and that radius isn’t a node any more.”

“Got it in one, Cathleen. Although I prefer to think of electrons as charge clouds rather than particles. Anyhow, when an atom has multiple charge concentrations their behavior is correlated. That opens the door to a flood of transitions between states that simply aren’t options for a single‑electron system. That’s why the visible spectrum of helium, with just one additional electron, has three times more lines than hydrogen does.”

“So do we walk away from spherical harmonics for atoms?”

“Oh, no, Susan, your familiar latitude and longitude harmonics fit well into the quantum framework. These days, though, we mostly use combinations of radial fade‑aways like my Sn00 example.”

~~ Rich Olcott

Completing The Triad

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

Walt’s mustache bristles as he gives me the eye. ”You claim three harmonics control how the Sun’s gravity could affect spacecraft orbits around a target planet like Jupiter. You said we don’t have to care about Jupiter’s gravitational zones and isolating the sectors probably isn’t doable. What’s the third?”

Time to twist the screws. ”Three harmonic systems, Walt, all working together and you’ve got their names wrong. They control nothing, they’re a framework for analysis. And Jupiter’s special. Solar gravity doesn’t affect its zonal harmonic arcs but that’s only because Jupiter’s polar axis is nearly perpendicular to its orbital plane. Zonal‑effect N‑S twisting at Jupiter is pennies on a C‑note. Any mission we send to Mars, Saturn or Uranus we’ll care a lot about their zonal harmonics because their axes have more tilt. An 82° tilt for Uranus, can’t get much more tilted than that. Sectorial harmonics may still help us navigate there because Uranus probably has a lot less magnetism than Jupiter.”

That rocks him but he comes back strong. ”The third kind of harmonic?!! C’mon, give!”

“Radial, the center‑out dimension. The gravitational force between bodies depends on center‑to‑center distances so yeah, your people would be interested.”

“I presume radial harmonics have numbers like Jn and Cm do?”

“They do. Sorry, this’ll get technical again but I’ll go as light as I can. Each radial harmonic is the product of two factors. You know about factors, right?”

“Sure, force multipliers.”

“You would know that kind. More generally, factors are things that get multiplied together. I’ll call the general radial harmonic Rn. It’s the product of two factors. The first is a sum of terms that begin with rn, where r is the distance. For instance, R3‘s first factor would look like a*r³+b*r²+c*r+d, where the a,b,c,d are just some numbers. Different radial harmonics have different exponents in their lead terms. You still with me?”

“Polynomials from high school algebra. Tell me something new.”

“The second factor decreases exponentially with n*r. No matter how large rn gets, when you multiply an rn polynomial by something that decreases exponentially, the (polynomial)×(exponential) product eventually gets really small.”

“Give me a second. … So what you’re saying is, at a big enough distance these radial harmonics just die away.”

“That’s where I was going.”

“How far is ‘enough’?”

“Depends on n. Higher values of n shut down faster.”

“So these Cms and Jns and Rns just add together?” <pauses, squints at me suspiciously> “Is there some reason you used n for both Jn and Rn?”

“No but yes, and yes. You combine a C, a J and an R using multiplication to get a full harmonic F, except there are rules. The J and R must belong to the same n. The m can’t be larger than n. From far away we’d model Jupiter’s gravity as F000=R0×J0×C0, which is an infinite sphere — R0 never dies away and J0×C0 says ‘no angular dependence.’ The Sun’s gravity acts along R0 and that’s what keeps Jupiter in orbit. If the problem demands combining full harmonics, you use addition.” <rousing a display on Old Reliable> “Here’s how a particular pair of harmonics combine to increase or decrease spherical gravity in specific directions.”

“But Juno doesn’t see those gravity lumps until it gets close‑in. How close?”

“R2‘s down to less than a part per thousand at three planetary radii, call it 225 000 kilometers away from the planet’s center.”

“How much time is it closer than that distance?”

“Complicated question. A precise answer requires some calculus — is your smart phone set up for elliptic integrals?”

“Of course not. A good estimate will do.”

“Okay, here’s the plan. What we’d like is total time spent while Juno travels along the ellipsoidal arc between points A and D where the orbit crosses the 225 000‑km circle. Unfortunately, Juno speeds up approaching point P, slows down going away — calculating the A‑D time is tricky. I’ll assume Juno travels straight lines AB and CD at the A-speed. I’ll also approximate the orbit’s close pass as a semicircle at P‑speed.” <tapping> “I get a 3.6-hour duration, less than 0.3% of the full 53-day orbit. Will that satisfy your people?”

“You’ll know if it doesn’t.”

~~ Rich Olcott

Sectorial Setbacks

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“Moire, you were holding out on me. Eddie’s, fifteen minutes.”

“Not so fast, Walt. That wasn’t me holding out, that was you leaving too soon. From now on you’re paying quite a bit more. And it’ll be thirty minutes.”

“So we’re negotiating, hmm?”

“That’s about the size of it. You still interested?”

“My people are, they sent me back here. Oh well. Thirty minutes.”

Thirty-three minutes later I walk into Eddie’s. Walt’s already gotten a table. He beckons, points to the freshly‑served pizza, raises an eyebrow.

“Apology accepted. What made your people unhappy?”

“You told me flat‑out that the Sun’s gravity couldn’t affect those zonal harmonics. Do you have anything to back that up?”

“Symmetry. Zonal harmonics and latitude are about north‑south. Each Jn is a pole‑to‑pole variation pattern. The only way solar gravity can tilt Jupiter’s north‑south axis is to exert torque along the zonal harmonics. Jupiter’s equator is within 3° of edge‑on to the Sun.” <showing an image on Old Reliable’s screen> “Here’s what the Sun sees looking at J10, for instance. Solar pull on any northern zone segment, say, would be counteracted by an equal pull on the corresponding southern segment of the same zone. No net torque, no tilt. J0‘s the only exception. It’s simply a sphere that doesn’t vary across the whole planet. The Sun’s pull along J0‘s arc can’t tilt Jupiter.”

“Okay, so the zonal picture’s too simple. Just one set of waves, running up and down the planet—”

“No, not running. One way to characterize a wave is by how its components change with time. You’re thinking like ocean waves that move from place to place as time goes by. There’s also standing waves like on a guitar string, where individual points move but the peaks and valleys don’t. There’s time‑only waves like how the day length here changes through the year. And there’s static waves where time’s not even in the equation. Jupiter’s stripes don’t move, they’re peaks and valleys in a static wave pattern. By definition, the zonal harmonic system is static like that. But you’re right, it’s only part of the picture.”

“Give me the part the Sun’s gravitational field does play with.”

“That’d be two parts — sectorial and radial harmonics. Sectorial is zonal’s perpendicular twin. Zonal wave patterns show variation along the polar axis; sectorial wave patterns Cm vary around it. I’m keeping it non‑technical for you but Cm‘s actually cos(m*x) where x is the longitude.”

“Just don’t let it go any farther.”

“I’ll try not to. My point is that each sector pattern can be labeled with a positive integer just like we did with the zones.”

“If the Jn arcs aren’t affected by solar gravity, why would I care about these Cms?”

“You wouldn’t, except for the fact that mass distribution across Jupiter’s sectors is probably lumpy. We know the Great Red Spot holds its position in the southern hemisphere and the planet’s magnetic field points way off to the side. Maybe those features mark off‑center mass deficits and concentrations. Suppose a particular sectorial wave’s peak sits directly over a mass lump or hole. Everything under that harmonic’s influence is tugged back and forth by solar gravity each time the wave traverses the day side. Juno in its N‑S path just isn’t an efficient sensor for those tugs. Good sectorial sensing would require an orbiter on an E‑W path, preferably right over the equator.  Any orbital wobbles we’d see could be fed into a sectorial gravity map. Cross that with the zonal map and we’d be able to locate underlying mass variations by latitude and longitude.”

“Not a good idea. Gravity’s not the only field in play. You’ve just mentioned Jupiter’s magnetic field. I’ve read it’s stronger than any other planet’s. If your E‑W orbiter’s built with even a small amount of iron, you’d have a hard time deciding which field was responsible for any observed irregularities.”

“Good point. The idea’s even worse than you think, though. Jupiter’s sulfur‑coated moon—”

“Io. Yes, your induction‑heating idea might even be real. What about it?”

“I haven’t written yet about the high‑voltage Io‑to‑Jupiter bridge made of sulfur, oxygen and hydrogen ions. Jupiter’s magnetism plays a complicated game with them but the result is a chaotic sheet of radiating plasma around the planet’s equator. An E‑W orbiter in there would be tossed about like a paper boat on the ocean.”

~~ Rich Olcott

A Pencil In Space

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, Physics: Newton and Gravity, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“I have a question I think you’ll find interesting, but it’s best we talk in person. Care for pizza?”

“If you’re buying.”

“Of course. Meet me at Eddie’s, twenty minutes. Bring Old Reliable.”

“Of course.”

Tall fellow, trimmed chevron mustache, erect bearing except when he’s leaning on that cane. “Moire?”

“That’s me. Good to meet you, Mr … ?”

“No names. Call me … Walt.”

We order, find a table away from the kitchen. “So, Walt, what’s this interesting question?”

“Been following this year’s Jupiter series in your blog. Read over the Kaspi paper, too, though most of that was over my head. What I did get was that his conclusions and your conclusions all come from measuring very small orbit shifts which arise from millionths of a g of force. Thing is, I don’t see where any of you take account of the Sun’s gravity. If the Sun’s pull holds Jupiter in orbit, it ought to swamp those micro-g effects. Apparently it doesn’t. Why not?”

“Well. That’s one of those simple questions that entail a complicated answer.”

“I’ve got time.”

“I’ll start with a pedantic quibble but it’ll clarify matters later on. You refer to g as force but it’s really acceleration. The one‑g acceleration at Earth’s surface means velocity changes by 980 meters/second per second of free fall. Drop a one kilogram mass, it’ll accelerate that fast. Drop a 100 kilogram mass, it’ll experience exactly the same acceleration, follow?”

“But the second mass feels 100 times the force.”

“True, but we can’t measure forces, only movement changes. Goes all the way back to Newton defining mass in terms of force and vice‑versa. Anyway, when you’re talking micro‑g orbit glitches you’re talking tiny changes in acceleration. Next step — we need the strength of the Sun’s gravitational field in Jupiter’s neighborhood.”

“Depends on the Sun’s mass and Jupiter’s mass. No, wait, just the Sun’s mass because that’s how it curves spacetime. The force depends on both masses.”

I’m impressed. “And the square of the very large distance between them.” <tapping on Old Reliable’s screen> “Says here the Sun’s field strength out there is 224 nano‑g, which is pretty small.”

“How’s that compare to what else is acting on Juno?”

<more tapping> “Jupiter’s local field strength crushes the Sun’s. At Juno’s farthest point it’s 197 micro‑g but at Juno’s closest point the field’s 22.7 million micro‑g and the craft’s doing 41 km/s during a 30-minute pass. Yeah, the Sun’s field would make small adjustments to Juno’s orbital speed, depending on where everybody is, but it’d be a very slow fluctuation and not the rapid shakes NASA measured.”

“How about side‑to‑side?”

“Good point, but now we’re getting to the structure of Juno’s orbit. Its eccentricity is 98%, a long way from circular. Picture a skinny oval pencil 8 million kilometers long, always pointed at Jupiter while going around it. It’s a polar orbit, rises above Jupiter on the approach, then falls below going away. The Sun’s effect is greatest when the orbit’s at right angles to the Sun‑Jupiter line. The solar field twists the oval away from N‑S on approach, trues it back up on retreat. That changes the angle at which Juno crosses Jupiter’s gravitational wobbles but won’t affect how it experiences the zonal harmonics.”

“Tell me about those zonal things.”

“A zone is a region, like the stripes on Jupiter, that circles a sphere at constant latitude. Technically, zonal harmonic Jn is the nth Legendre polynomial in cos(θ)—”

“Too technical.”

“Gotcha. Okay, each Jn names a shape, a set of gravitational ripples perpendicular to the polar axis. J0‘s a sphere with no ripples. Jupiter’s average field looks like that. A bigger n number means more ripples. Kaspi’s values estimate how much each Jn‘s intensity adds to or subtracts from J0‘s strength at each latitude. The Sun’s field can modify the intensity of J0 but none of the others.”

Walt grabs his cane, stands, drops a C‑note on the table. “This’ll cover the pizza and your time. Forget we had this conversation.” And he’s gone.

“Don’t mention it.”

~~ Rich Olcott

  • Thanks to Will, who asked the question.

Screaming Out Of Space

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, UncategorizedLeave a comment

Cal (formerly known as Al) comes over to our table in his coffee shop. “Lessee if I got this right. Cathleen is smug twice. First time because the new results from Juno‘s data say her hunch is right that Jupiter’s atmosphere moves like cylinders inside each other. Nearly cylinders, anyhow. Second smug because Sy used the Juno data to draw a math picture he says shows the Great Red Spot but I’m lookin’ at it and I don’t see how your wiggle‑waggles show a Spot. That’s a weird map, so why’re you smug about it, Cathleen?”

“The map’s weird because it’s abstract and way different from the maps you’re used to. It’s also weird because of how the data was collected. Sy, you tell him about the arcs.”

“Okay. Umm… Cal, the maps you’re familiar with are two‑dimensional. City maps show you north‑south and east‑west, that’s one dimension for each direction pair. Maps for bigger‑scale territories use latitude for north‑south and longitude for east‑west but the principle’s the same. The Kaspi group’s calculations from Juno‘s orbit data give us a recipe for only a one‑dimensional map. They show how Jupiter’s gravity varies by latitude, nothing about longitude. We could plot that as a rectangle, latitude along the x‑axis, relative strength along the y‑axis. I thought I’d learn more by wrapping the x‑axis around the planet so we could look for correlations with Jupiter’s geography. I found something and that’s why Cathleen’s smug. Me, too.”

“Why latitude but nothing about longitude?”

“Because of the way Juno‘s orbit works. The spacecraft’s not hovering over the planet or even circling it like the ISS circles Earth. NASA wanted to minimize Juno‘s exposure to Jupiter’s intense magnetic and radiation fields. The craft spends most of its 53‑day orbit at extreme distance, up to millions of kilometers out. When it approaches, it screams in at about 41 kilometers per second, that’s 91 700 mph, on a mostly north‑to‑south vector so it sees all latitudes from a few thousand kilometers above the cloud‑tops. Close approach lasts only about three hours, for the whole planet, and then the thing is on its way out again. During that three hours, the planet rotates about 120° underneath Juno so we don’t have a straight vertical N‑S pass down the planet’s face. Gathering useful longitude data’s going to take a lot more orbits.”

“So you’re sayin’ Juno felt gravity glitches at all different angles going pole to pole, but only some of the angles going round and round.”

“Exactly.”

“So now explain the wiggle‑waggles.”

“They represent parts‑per‑million variations in the field pulling Juno towards Jupiter at each latitude. Where the craft is over a more massive region it’s pulled a bit inwards and Sy’s map shows that as a green bump. Over a lighter region Juno‘s free to move outward a little and the map shows a pink dip. Kaspi and company interpret the heaviness just north of the equator to be a dense inward flow of gas all around the planet. Maybe it is. Sy and I think the pink droplet south of the equator could reflect the Great Red Spot lowering the average mass at its latitude. Maybe it is. As always, we need more data, okay? Now I’ve got questions for you, Sy.”

“Shoot.”

“You built your map by multiplying each Jn‑shape by its Kaspi gravitational intensity then adding the multiplied shapes together. But you only used Jn‑shapes with integer names. Is there a J½?”

“Some mathematicians play with fractional J‑thingies but I’ve not followed that topic.”

“Understandable. Next question — the J‘s look so much like sine waves. Why not just use sine‑shapes?”

“I used Jn‑shapes because that’s how Kaspi’s group stated their results. They had no choice in the matter. Jn‑shapes naturally appear in spherical system math. The nice thing about Jn‑shapes is that n provides a sort of wavelength scale. For instance, J35 divides Jupiter’s pole‑to‑pole arc into 36 segments each as wide as Earth’s diameter. Here’s a plot of intensity against n.”

Adapted from Kaspi, Figure 2a

“Left to right, red light to blue.”

“Exactly.”

~ Rich Olcott

Zoning Out over Jupiter

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, Physics: Waves, UncategorizedLeave a comment

I’m nursing my usual mug of eye‑opener in Cal’s Coffee Shop when astronomer Cathleen and chemist Susan chatter in. “Morning, ladies. Cathleen, prepare to be even more smug.”

“Ooo, what should I be smug about?”

“Your Jupiter suggestion. Grab some coffee and a couple of chairs.” <screen‑tapping on Old Reliable> “Ready? First step — purple and violet. You’ll never see violet or purple light coming from a standard video screen.”

“He’s going spectrum‑y on us, right, Cathleen?”

“More like anti‑spectrum‑y, Susan. Purple light doesn’t exist in the spectrum. We only perceive that color when we see red mixed with blue like that second band on Sy’s display. Violet light is a thing in nature, we can see it in flowers and dyes and rainbows beyond blue. Standard screens can’t show violet because their LEDs just emit red, blue and green wavelengths. Old Reliable uses mixtures of those three to fake all its colors. Where are you going with this, Sy?””

“Deeper into Physics. Cast your eyes upon the squiggles to the right. The one in the middle represents the lightwave coming from purple‑in‑the‑middle. The waveform’s jaggedy, but if you compare peaks and troughs you can see its shape is the sum of the red and blue shapes. I scaled the graphs up from 700 nanometers for red and 450 for blue.”

“Straightforward spectroscopy, Sy, Fourier analysis of a complicated linear waveform. Some astronomers make their living using that principle. So do audio engineers and lots of other people.”

“Patience, Cathleen, I’m going beyond linear. Fourier’s work applies to variation along a line. Legendre and Poisson extended the analysis to—”

“Aah, spherical harmonics! I remember them from Physical Chemistry class. They’re what gives shapes to atoms. They’ve got electron shells arranged around the nucleus. Electron charge stays as close to the nucleus as quantum will let it. Atoms absorb light energy by moving charge away from there. If the atom’s in a magnetic field or near other atoms that gives it a z-axis direction then the shells split into wavey lumps going to the poles and different directions and that’s your p-, d– and f-orbitals. Bigger shells have more room and they make weird forms but only the transition metals care about that.”

The angular portion of the lowest-energy spherical harmonics
Credit: Inigo.quilez, under CCA SA 3.0 license
Adapted from Wieczorek and Meschede under CC BY-NC-ND 4.0

“Considering you left out all the math, Susan, that’s a reasonable summary. I prefer to think of spherical harmonics as combinations of wave shapes at right angles. Imagine a spherical blob of water floating in space. If you tap it on top, waves ripple down to the bottom and back up again and maybe back down again. Those are zonal waves. A zonal harmonic averages over all E‑W longitudes at each N‑S latitude. Or you could stroke the blob on the side and set up a sectorial wave pattern that averages latitudes.”

“How about center‑out radial waves?”

“Susan’s shells do that job. My point was going to be that what sine waves do for characterizing linear things like sound and light, spherical harmonics do for central‑force systems. We describe charge in atoms, yes, but also sound coming from an explosion, heat circulating in a star, gravity shaping a planet. Specifically, Jupiter. Kaspi’s paper you gave me, Cathleen, I read it all the way to the Results table at the tail end. That was the rabbit‑hole.”

“Oh? What’s in the table?”

“Jupiter’s zonal harmonics — J‑names in the first column, J‑intensities in the second. Jn‘s shape resembles a sine wave and has n zeroes. Jupiter’s never‑zero central field is J0. Jn increases or decreases J0‘s strength wherever it’s non‑zero. For Jupiter that’s mostly by parts per million. What’s cool is the pattern you see when you total the dominating Jeven contributions.”

Data from Kaspi, et al.

Cathleen’s squinting in thought. “Hmm… green zone A would be excess gravity from Jupiter’s equatorial bulge. B‘s excess is right where Kaspi proposed the heavy downflow. Ah‑HAH! C‘s pink deficit zone’s right on top of the Great Red Spot’s buoyant updraft. Perfect! Okay, I’m smug.”

~ Rich Olcott

Revising The Model

On By rolcottIn Astronomy: Planetary Science, Uncategorized4 Comments

Cathleen’s perched at a table in Cal’s Coffee Shop, sipping a latte and looking smug. “Hi, Sy.”

“Hi, yourself. Did somebody you don’t like get a well‑deserved comeuppance?”

“Nothing that juicy. Just an old hunch that’s gotten some strong new supporting evidence. I love it when that happens.”

“So what’s the hunch and what’s the evidence?”

“You’ve already heard the hunch.” <dialing up an image on her phone> “Remember this sketch?”

“Hmmm, yeah, you and Vinnie were debating Jupiter’s atmosphere. Its massive airflows could self‑organize as an oniony nest of concentric spherical shells, or maybe concentric cylinders like that picture on your phone. Later on Vinnie thought up a more dynamic option — cylindrical shells encasing sets of smaller tornados like roller bearings. You shot that one down, right?”

“Mostly. I did admit something like that might work at the poles. Anyway, I’ve liked the concentric cylinders model for quite a while. This paper I just read says I’m almost but not quite right. Kaspi and company’s data says the cylinders are cone sections, not cylinders, and they’re not north‑south symmetrical.” <dialing up another image> “It’s like this except I’ve exaggerated the angles.”

“Doesn’t look all that different to me. Congratulations on the near‑win. What’s the new model based on? Did Juno drop another probe into the atmosphere?”

“Nope. Remote sensing, down as far as 3000 kilometers.”

“I thought Jupiter’s cloud decks blocked infrared.”

“Another nope. Not infrared sensing, gravity.”

“Didn’t know Juno carried a gravimeter.”

“It doesn’t, that’d be way too heavy and complex. Juno itself was the remote sensor. Whenever NASA’s Deep Space Network captured a data transmission from Juno, they also recorded the incoming radio signal’s precise frequency. Juno‘s sending frequency is a known quantity. Red‑shifts and blue‑shifts as received told us Juno‘s then‑current velocity relative to Earth. The shifts are in the parts‑per‑million range, tiny, but each speed‑up or slow‑down carries information about Jupiter’s gravitational field at that point in Juno‘s orbit. Given velocity data for enough points along enough orbits, you can build a gravity atlas. This paper reports what the researchers got from orbits 1 through 37.”

“Cute idea. They’ve built the atlas, I suppose, but what can gravity say about your wind cylinders?”

“Winds in Jupiter’s atmosphere are driven by heat rising from the core. Put a balloon 3000 kilometers down. Heated air inside the balloon expands. That has two effects. One, the balloon is less dense than its surroundings so it rises. Two, the work of expanding against outside pressure drains thermal energy and cools the balloon’s air molecules. The process continues until the balloon gets up to where its temperature and pressure match what’s outside, right?”

“Which is probably going to be well above 3000 kilometers. Hmm… if you’ve got lots of balloons doing that, as they fly upward they leave a vacuum sort of. Excess balloons up top will be pulled downward to fill the void.”

“Now organize all those balloons in a couple of columns, one going up and one down. Will they have equal mass?”

“Interesting. No, they won’t. The rising column rises because it’s less dense than its surroundings and the falling column falls because it’s more dense. More mass per unit volume in the falling column so that’s heavier.”

“Eighteenth Century Physics. Planetary rotation forces columns of each kind to merge into a nest of separate cones. Rising‑column warm cones support Jupiter’s white ammonia‑ice zones. Falling‑column cool cones disclose red‑brown belts. The gravity field is stronger above the dense falling regions, weaker over the light rising ones. Juno responded to gravity’s wobbles; the researchers built their models to fit Juno‘s wobbles. The best models aren’t quite concentric cylinders, because the cones tilt poleward. This graphic tells the story. The rectangle shows a 3000‑kilometer vertical section. The between-shell boundaries are effective — the paper specifically says that mass transport inward from the outermost shell is insignificant.”

Adapted from NASA/JPL-Caltech/SSI/SWRI/MSSS/ASI/ INAF/JIRAM/Björn Jónsson
CC BY 3.0

“You said the data’s asymmetric?”

“Yep. The strongest part of the gravitational signal came from flow angling down and equator‑ward, 21°N to 13°N.”

“Why’s that?”

“Maybe the Great Red Spot down south drives everything northward. We don’t know.”

~ Rich Olcott

Big Spin May Make Littler Spins

On By rolcottIn Astronomy: Planetary Science, UncategorizedLeave a comment

“Sorry, Vinnie, if there’s anything to your ‘Big Skip‘ idea you can’t blame Jupiter’s Great Red Spot on Io.”

“Come again, Cathleen? Both you and Sy were acting intrigued.”

“That was before I looked up a few numbers. You suggested that a long‑ago grazing collision between Io and Jupiter could account for Jupiter’s weird off‑center magnetic field, its Great Red Spot and Io’s heat and paltry waterless atmosphere. The problem is, there’s two big pieces of evidence against you. The first is Io’s orbit. It’s almost a perfect circle, eccentricity 0.0041, less than half the average of the other Galilean moons. A true circle has zero eccentricity compared to a parabola at 1.0.”

“So why is that evidence against the idea?”

“There’s virtually zero probability that a chaotic skip would send Io directly into such a perfect orbit. Okay, repetitive tugs from Ganymede’s and Europa’s gravity fields could conceivably have acted together to circularize and synchronize Io’s behavior but that would take millions of years.”

“So it’d take a while. Who’s in a hurry?”

“Your idea is, because of the second piece of evidence. Jupiter is a fluid planet, gaseous‑fluid much of the way in, liquid‑fluid most of the rest, right? Lots of up‑and‑down circulation due to outward heat flow from Jupiter’s core, plus twisty Coriolis winds at all levels powered by the planet’s rotation. All that commotion would smear out any trace of your grazing collision, probably within a hundred thousand years. The scars from Shoemaker-Levy’s impact on Jupiter were gone within months. Circularization’s too slow, smearing’s too fast, idea’s pfft.”

“Oh well, another beautiful picture bites the dust.” Vinnie glances up and to the left, the thing he does when he’s visualizing stuff. (On him, a quick glance up and to the right is a bluff tell but he knows I know which makes things interesting.) “Okay, so we’re thinking about how Jupiter’s weird atmosphere and how its equator rotates faster than its poles. That cylinder spinning inside a spinning cylinder idea looks nice for an explanation but I can think of a different way it could happen. How about like a roller bearing?”

“Hmm?”

“Big spinning columns deep inside all around the planet. Think about what goes on in between those cylinders you talked about — two layers flowing at different speeds right next to each other. There’s gonna be all kinds of watchacallit – turbulence – in there, trying to match things up but it can’t. Sooner or later twisters are gonna grow up to be north‑south columns.”

“He’s got a point, Cathleen. His columns would reduce between‑layer friction at the cost of increased between‑column friction. Depending on conditions that could give a lower‑energy, more stable configuration.”

“Spoken like a true physicist, Sy. Columns may be part of the story, but not all of it. There’s mostly‑for evidence but also really‑against evidence.”

Adapted from images by NASA/JPL-Caltech/SwRI/ASI/INAF/JIRAM

“Give us the ‘mostly‑for,’ make us feel good.”

“You guys.” <drawing tablet from her purse, tapping screen> “Alright, here’s a couple of images that Juno sent us when it orbited over Jupiter’s poles.”

“Sure looks like what was in my mind. I’ve seen that before somewhere…. Yeah, Al had that poster up behind his cash register like five years ago.”

“Impressive memory, Vinnie. Anyway, those vortices are similar to your idea, except look at these images critically.”

“Wait, different whirlpool counts top and bottom.”

“Right. These columns obviously don’t go all the way through. They must extend only partway inward until they’re blocked at some lower level.”

“Why can’t I have my columns all the way through if they’re outside the blocking level?”

“You could and there may be something like that inside the Sun, but that’s probably not the case for Jupiter.”

“Why not?”

“That’s the ‘really‑against’ evidence — the Great Red Spot and Jupiter’s off‑center magnetism. Something’s powerful enough to cause those two massive phenomena. That something would disrupt your ring‑in‑a‑ring rotation, at least down to the level where the disrupter lives. Your columns could only operate in some layer deeper than the disrupter’s level but above whatever’s blocking the polar columns. If there is such a layer.”

“Geez. Well, a guy can still hope.”

“But that’s not Science.”

~~ Rich Olcott

The Big Skip?

On By rolcottIn Astronomy: Planetary Science, UncategorizedLeave a comment

Suddenly Vinnie gets a grin all over his face. “Tell me something, Cathleen. Suppose I’m a pilot in a shuttle craft like in Star Trek. Tell me how conditions change as I dive down into Jupiter.”

“Hmm .. okay. Mind you, it’ll be a dangerous flight. You’ll fly through an atmosphere that’s mostly molecular hydrogen which is notorious for sneaking into metallic materials and weakening them. I recommend investing in a Starfleet‑grade force shield to keep the atmosphere completely away from your hull. While you’re in the stratosphere high above the cloud decks you’ll see a deep blue sky pretty much the same as Earth’s stratosphere. Try to avoid the thin gray clouds in the upper troposphere — their greasy hydrocarbons will fog your windshield. You want to stick to clear air as much as possible so dodge around the white ammonia‑ice zones. You can drop a couple hundred kilometers more before you hit the top of a brownish ammonium sulfides band.”

“Once I’m that deep there’s clear air underneath the white deck, right?”

“We just don’t know. Unlikely, but if you do want to fly beneath a zone you’ll have to traverse the jetstream separating it from your band. Pick the pole‑ward zone — jetstreams on that side seem to host fewer thunderstorms. Strap in for the jump, because the jetstreams sustain windspeeds 2‑3 times what we get in a Category 5 hurricane. Things’ll get muddier when you drop beneath the brown clouds.”

“Brown as mud, uh-huh.”

“No, I mean literal mud, maybe. First there’s a water‑ice layer and below that there may be a layer of clay‑ish or silicate droplets which may include water of crystallization. I like to visualize clouds of opal, but of course there’d be no sunlight to see them by. A bit lower and you’ll fly through helium rain. Get past all that and you’re about 20% of the way down, about two Earth diameters.”

“That’s where I bump into something?”

“No, that’s the transition zone where heat and pressure convert molecular H₂ into a metallic fluid of protons embedded in a conducting ocean of electrons. Sy, how do you suppose that would affect Vinnie’s aerodynamics?”

“Destructively. If his shuttle’s skin doesn’t rupture he’d be floating rather than sinking. Net density of an intact hull and everything inside would be less than the prevailing density outside where protons are crammed together. Even powered descent would be tough.”

“Sy, that’s exactly what my crazy idea needs! Cathleen, when’s your next Crazy Theory seminar?”

“Not until next term, some time in the Fall. C’mon, Vinnie, out with it!”

Magnetism and wind map by NASA/JPL-Caltech/SwRI/John E. Connerney. Great Red Spot image added by the author.

“All right. That diagram you showed us with the red and blue spots in Jupiter’s off‑center magnetic field? It got me thinking. You get magnetism from moving charge, right, and they say Earth’s field comes from swirls in the molten iron deep underneath our crust. Jupiter doesn’t have iron so much, but you say it’s got electrons in liquid metallic hydrogen and that oughta be able to swirl, too. Maybe Jupiter has a shallow major swirl on that one side.”

“And just what do you suggest would cause a swirl like that?”

“Al was talking the other day about ‘the grand tack hypothesis‘ where Jupiter waltzed in across the inner Solar System before it waltzed back out and settled down where it’s at. Suppose while it was waltzing it hit a planetoid, maybe the size of Io. The little guy couldn’t sink and wouldn’t stick because metallic hydrogen’s liquid so it’d skip across the surface and shoot away and maybe became a moon. That’d raise a swirl like I’m talking about. See, on the map a line crossing the line between the magnetic red and blue spots could be the skip path.”

<silence>

“Hey, and the Great Red Spot, see how it’s like opposite to where I guess the hit was, that’d be like a through-planet resonance like on Mars where that Hellas meteor strike is opposite the Tharsis Bulge.”

<long pause>

“I dunno, Cathleen, Io’s so weird, do you suppose…”

“I dunno, Sy. Io has that magnetic bridge to Jupiter…”

~ Rich Olcott

Stripes And Solids

On By rolcottIn Astronomy: Planetary Science, Uncategorized3 Comments

“Any other broad-brush Jupiter averages, Cathleen?”

“How about chemistry, Vinnie? Big picture, 84% of Jupiter’s atoms are hydrogen, 16% are helium.”

“Doesn’t leave much room for asteroids and such that fall in.”

“Less than a percent for all other elements. Helium doesn’t do chemistry, so from a distant chemist’s perspective Jupiter and Saturn both look like a dilute hydrogen‑helium solution of every other element. But the solvent’s not a typical laboratory liquid.”

“Hard to think of a gas as a solvent.”

“True, Sy, but chemistry gets strange under high temperatures and pressures.”

“Hey, I always figured Jupiter to be cold ’cause it’s farther from the Sun than us.”

“Good logic, Vinnie, but Jupiter generates its own heat. That’s one reason its weather is different from ours. Earth gets more than 99% of its energy budget from sunlight, especially in the infrared. There’s year‑long solar heating at low latitudes but only half‑years of that near the Poles. The imbalance is behind the temperature disparities that drive our prevailing weather patterns.”

“Jupiter’s not like that?”

“Nope. It gets 30 times less energy from the Sun than Earth does and actually gives off more heat than it receives. Its poles and equator are at virtually the same chilly temperature. There’s a small amount of heat flow from equator to poles, but most of Jupiter’s heat migrates spherically from a 24,000 K fever near its core to its outer layers.”

“What could generate all that heat?”

“Probably several contributors. The dominant one is gravitational potential energy from everything falling inward and banging into everything else. Random rock or atom collisions generate heat. Entropy rules.”

“Sounds reasonable. What’s another?”

“Radioactives. Half of Earth’s internal heating comes from gravity, same mechanism as Jupiter though on a smaller scale. The rest comes from unstable isotopes like uranium, thorium and potassium‑40. Also aluminum‑26, back in the early years, but that’s all gone now. Jupiter undoubtedly ate from the same dinner table. Those fissionable atoms split and release heat whenever they feel like it whether or not they’re collected in one place like in a reactor or bomb. Whatever the origin, Jupiter ferries that heat to the surface and dumps it as infrared radiation.”

“Yeah or else it’d explode or something.”

“Mm-hm. The question is, what are the heat‑carrying channels? They must thread their way through the planet’s structure.”

“It’s just a big ball of gas, how can it have structure?”

“I can help with that, Vinnie. Remember a few years back I wrote about high‑pressure chemistry? Hydrogen gets weird at a million bars‑‑‑”

“Anyone’d get weird after that many bars, Sy.” <heh, heh>

“Ha ha, Vinnie. A bar is pressure equal to one Earth atmosphere. Pressures deep inside Jupiter get into hundreds of megabars. Hydrogen molecules down there are crammed so close together that their electron clouds merge and you have a collection of protons floating in a sea of electron charge. They call it metallic hydrogen, but it’s fluid like mercury, not crystalline. Cathleen, when you refer to Jupiter’s structure you’re thinking layers?”

“That’s right, Sy, but the layers may or may not be arranged like Earth’s crust, mantle, core scheme. A lot of the Juno data is consistent with that — a shell of the atmosphere we see, surrounding a thick layer of increasingly compressed hydrogen‑helium over a core of heavy stuff suspended in metallic hydrogen. About 20% down we think the helium is squeezed out and falls like rain, only to evaporate again at a lower level. The core’s metallic hydrogen may even be solid despite thousand‑degree temperatures — we just don’t know how hydrogen behaves in that regime.”

“What other kind of layering can there be?”

“Experiments have demonstrated that under the right conditions a rapidly spinning fluid can self-organize into a series of concentric rotating cylinders. Maybe Jupiter and the other gas planets follow that model and the stripes show where the cylinders intersect with gravity’s spherical imperative. Coaxial cylinders would account for the equator and poles rotating at different rates. Juno data indicates that Jupiter’s equatorial zone has more ammonia than the rest of its atmosphere. Maybe between‑cylinder winds trap the ammonia and prevent it from mixing with the next deeper cylinder.”

~ Rich Olcott