Tag: Newton

Flipping An Edge Case

On By rolcottIn Chemistry, Physics: Quantum Mechanics, UncategorizedLeave a comment

“Why’s the Ag box look weird in your chart, Susan?”

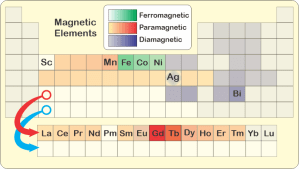
“That’s silver, Eddie. It’s an edge case. The pure metal’s diamagnetic. If you alloy silver with even a small amount of iron, the mixture is paramagnetic. How that works isn’t my field. Sy, it’s your turn to bet and explain.”

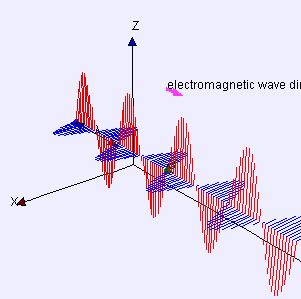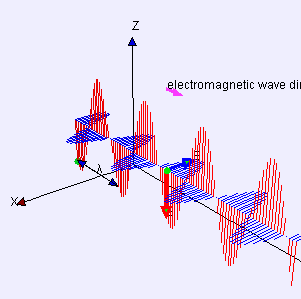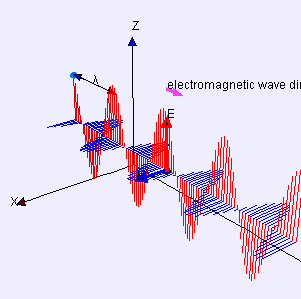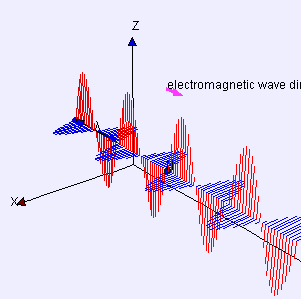
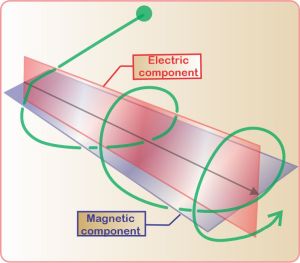
I match Eddie’s bet (the hand’s not over). “It’s magnetism and angular momentum and how atoms work, and there are parts I can’t explain. Even Feynman couldn’t explain some of it. Vinnie, what do you remember about electromagnetic waves?”

“Electric part pushes electrons up and down, magnetic part twists ’em sideways.”

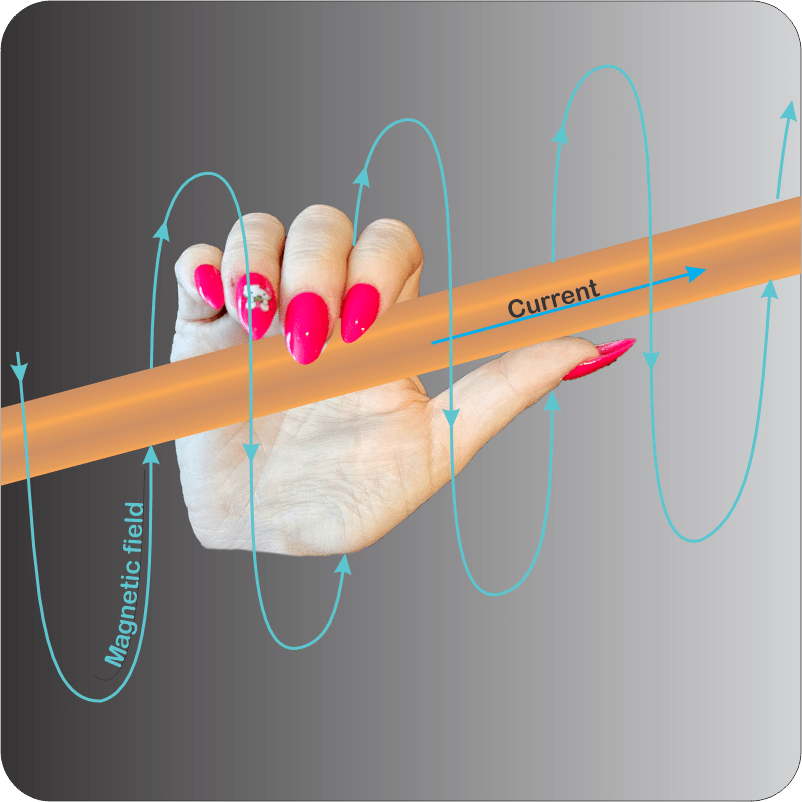
“Good enough, but as Newton said, action begets reaction. Two centuries ago, Ørsted discovered that electrons moving along a wire create a magnetic field. Moving charges always do that. The effect doesn’t even depend on wires — auroras, fusion reactor and solar plasmas display all sorts of magnetic phenomena.”

“You said it’s about how atoms work.”

“Yes, I did. Atoms don’t follow Newton’s rules because electrons aren’t bouncing balls like those school‑book pictures show. An electron’s only a particle when it hits something and stops; otherwise it’s a wave. The moving wave carries charge so it generates a magnetic field proportional to the wave’s momentum. With me?”

“Keep going.”

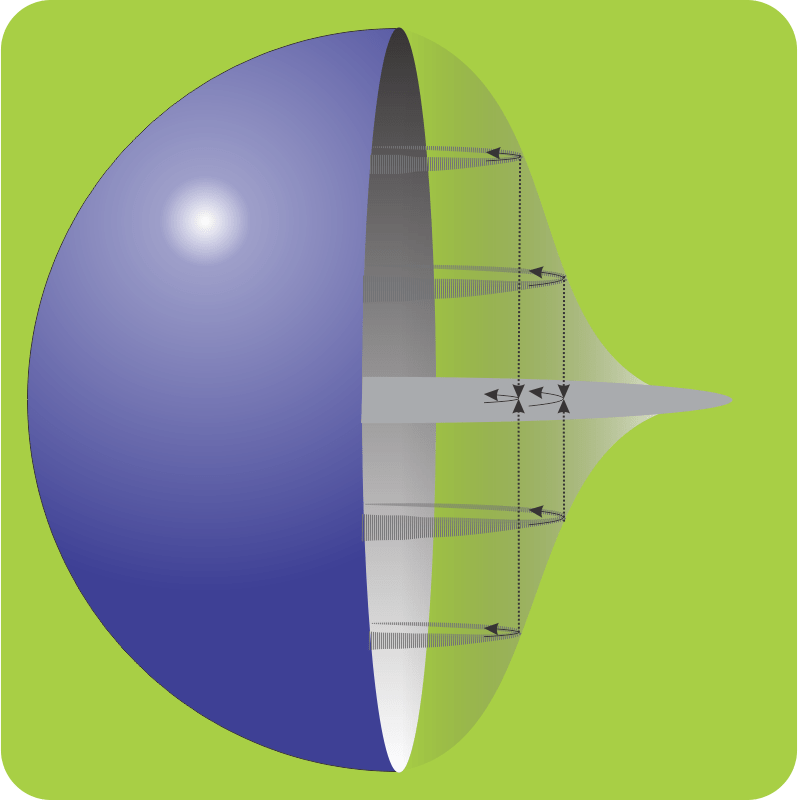
“That picture’s fine for a wave traveling through space, but in an atom all the charge waves circle the nucleus. Linear momentum in open space becomes angular momentum around the core. If every wave in an atom went in the same direction it’d look like an electron donut generating a good strong dipolar magnetic field coming up through the hole.”

“You said ‘if’.”

“Yes, because they don’t do that. I’m way over‑simplifying here but you can think of the waves pairing up, two single‑electron waves going in opposite directions.”

“If they do that, the magnetism cancels.”

“Mm‑hm. Paired‑up configurations are almost always the energy‑preferred ones. An external magnetic field has trouble penetrating those structures. They push the field away so we classify them as diamagnetic. The gray elements in Susan’s chart are almost exclusively in paired‑up configurations, whether as pure elements or in compounds.”

“Okay, so what about all those paramagnetic elements?”

The angular portion of the lowest-energy spherical harmonic modes
Credit: Inigo.quilez, under CCA SA 3.0 license

“Here’s where we get into atom structure. An atom’s electron cloud is described by spherical harmonic modes we call orbitals, with different energy levels and different amounts of angular momentum — more complex shapes have more momentum. Any orbital hosting an unpaired charge has uncanceled angular momentum. Two kinds of angular momentum, actually — orbital momentum and spin momentum.”

“Wait, how can a wave spin?”

“Hard to visualize, right? Experiments show that an electron carries a dipolar magnetic field just like a spinning charge nubbin would. That’s the part that Feynman couldn’t explain without math. A charge wave with spin and orbital angular momentum is charge in motion; it generates a magnetic field just like current through a wire does. The math makes good predictions but it’s not something that everyday experience prepares us for. Anyway, the green and yellow‑orange‑ish elements feature unpaired electrons in high‑momentum orbitals buried deep in the atom’s charge cloud.”

“So what?”

“So when an external magnetic field comes along, the atom’s unpaired electrons join the party. They orient their fields parallel to the external field, in effect allowing it to penetrate. That qualifies the atom as paramagnetic. More unpaired electrons means stronger interaction, which is why iron goes beyond paramagnetic to ferromagnetic.”

“How does iron have so many?”

“Iron’s halfway across its row of ten transition metals—”

“I know where you’re going with this, Sy. It’ll help to say that these elements tend to lose their outer electrons. Scandium over on the left ionizes to Sc3+ and has zero d‑electrons. Then you add one electron in a d orbital for each move to the right.”

“Thanks, Susan. Count ’em off, Vinnie. Five steps over to iron, five added d‑electrons, all unpaired. Gadolinium, down in the lanthanides, beats that with seven half‑filled f‑orbitals. That’s where the strength in rare earth magnets arises.”

“So unpaired electrons from iron flip alloyed silver paramagnetic?”

“Vinnie wins this pot.”

~ Rich Olcott

A No-Charge Transaction

On By rolcottIn Cosmology, Crazy Theories, Physics: Light and Relativity, UncategorizedLeave a comment

“I ain’t done yet, Sy. I got another reason for Dark Matter being made of faster‑then‑light tachyons.”

“I’m still listening, Vinnie.”

“Dark Matter gotta be electrically neutral, right, otherwise it’d do stuff with light and that doesn’t happen. I say tachyons gotta be neutral.”

“Why so?”

“Stands to reason. Suppose tachyons started off as charged particles. The electric force pushes and pulls on charges hugely stronger than gravity pulls—”

“1036 times stronger at any given distance.”

“Yeah, so right off the bat charged tachyons either pair up real quick or they fly away from the slower‑than‑light bradyon neighborhood leaving only neutral tachyons behind for us bradyon slowpokes to look at.”

“But we’ve got un‑neutral bradyon matter all around us — electrons trapped in Earth’s Van Allen Belt and Jupiter’s radiation belts, for example, and positive and negative plasma ions in the solar wind. Couldn’t your neutral tachyons get ionized?”

“Probably not much. Remember, tachyon particles whiz past each other too fast to collect into a star and do fusion stuff so there’s nobody to generate tachyonic super‑high‑energy radiation that makes tachyon ions. No ionized winds either. If a neutral tachyon collides with even a high-energy bradyon, the tachyon carries so much kinetic energy that the bradyon takes the damage rather than ionize the tachyon. Dark Matter and neutral tachyons both don’t do electromagnetic stuff so Dark Matter’s made of tachyons.”

“Ingenious, but you missed something way back in your initial assumptions.”

“Which assumption? Show me.”

“You assumed that tachyon mass works the same way that bradyon mass does. The math says it doesn’t.” <grabbing scratch paper for scribbling> “Whoa, don’t panic, just two simple equations. The first relates an object’s total energy E to its rest mass m and its momentum p and lightspeed c.”

E² = (mc²)² + (pc)²

“I recognize the mc² part, that’s from Einstein’s Equation, but what’s the second piece and why square everything again?”

“The keyword is rest mass.”

“Geez, it’s frames again?”

“Mm‑hm. The (mc²)² term is about mass‑energy strictly within the object’s own inertial frame where its momentum is zero. Einstein’s famous E=mc² covers that special case. The (pc)² term is about the object’s kinetic energy relative to some other‑frame observer with relative momentum p. When kinetic energy is comparable to rest‑mass energy you’re in relativity territory and can’t just add the two together. The sum‑of‑squares form makes the arithmetic work when two observers compare notes. Can I go on?”

“I’m still waitin’ to hear about tachyons.”

“Almost there. If we start with that equation, expand momentum as mass times velocity and re‑arrange a little, you get this formula

E = mc² / √(1 – v²/c²)

The numerator is rest‑mass energy. The v²/c² measures relative kinetic energy. The Lorentz factor down in the denominator accounts for that. See, when velocity is zero the factor is 1.0 and you’ve got Einstein’s special case.”

“Give me a minute. … Okay. But when the velocity gets up to lightspeed the E number gets weird.”

“Which is why c is the upper threshold for bradyons. As the velocity relative to an observer approaches c, the Lorentz factor approaches zero, the fraction goes to infinity and so does the object’s energy that the observer measures.”

“Okay, here’s where the tachyons come in ’cause their v is bigger than c. … Wait, now the equation’s got the square root of a negative number. You can’t do that! What does that even mean?”

“It’s legal, when you’re careful, but interpretation gets tricky. A tachyon’s Lorentz factor contains √(–1) which makes it an imaginary number. However, we know that the calculated energy has to be a real number. That can only be true if the tachyon’s mass is also an imaginary number, because i/i=1.”

“What makes imaginary energy worse than imaginary mass?”

“Because energy’s always conserved. Real energy stays that way. Imaginary mass makes no sense in Newton’s physics but in quantum theory imaginary mass is simply unstable like a pencil balanced on its point. The least little jiggle and the tachyon shatters into real particles with real kinetic energy to burn. Tachyons disintegrating may have powered the Universe’s cosmic inflation right after the Big Bang — but they’re all gone now.”

“Another lovely theory shot down.”

~ Rich Olcott

Properties of Space

On By rolcottIn Cosmology, Physics: Electromagnetism, Physics: Waves, UncategorizedLeave a comment

Vinnie gives me the side‑eye. “Wait, Sy. Back there you said Maxwell got the speed of light from the properties of space. What does any of that even mean?”

“Do you remember Newton’s equation for the force of gravity between two objects?”

“Of course not. Lessee… the force’d be bigger when either one gets bigger, and it’d get smaller when the distance between ’em gets bigger and there’s some constant number to make the units right, right?”

“Close enough, it’s the distance squared. The equation’s F=Gm1m2/r². The G is the constant you mentioned. It does more than turn mass‑units times mass‑units divided by length‑units‑squared into force‑units. It says how many force‑units. For one pair of objects at a certain distance, turn the G‑dial up and you get more force. Make sense?”

“Yeah, that looks right.”

“The value of G sets the force‑distance scale for how two objects attract each other everywhere in the Universe. That value is a property of space. So is the fact that the value is the same in all directions.”

“Huh! Never thought of it like a scale factor. Space has other properties like that?”

“Certainly. Coulomb’s Law for the electrostatic force between two charged objects has the same basic structure, FE=–(q1q2/r²)/CE. In any units you like you replace the q‘s with object charge amounts and r with the distance between them. For each set of change‑ and distance‑units there’s a well‑researched value of CE to convert your charge and distance numbers into force‑units. Under the covers, though, CE is a scale factor that controls the range of the electrostatic force. It’s the same everywhere in the Universe and it’s completely independent of Newton’s gravity scale factor.”

“Hey, what about ‘like charges repel, opposites attract’?”

“That’s what the minus sign’s in there for. If the q‘s have the same charge, the force is negative, that’s repulsion; opposite charges make for positive, attractive force.”

“If there’s a CE for electric there’s gotta be a CM for magnetic.”

“Sort of. The electrostatic force doesn’t care about direction. Magnetism does care so the equation’s more complicated. You’re right, though, there is a similar universal scale factor we might as well call CM.”

<chuckle> “Electric, magnetic, I don’t suppose we could mix those two somehow for an electromagnetic scale factor?”

<grin> “Did you read ahead in the book? Yes we can, and Maxwell’s equations showed us how. If you multiply the two C‘s together, you get one over the square of the speed of light. Re‑arranging a little, c=√(1/CECM), so c, the electromagnetic scale factor for velocity, is based on those space properties. Einstein showed that no material object can have a velocity greater than c.”

“I’ll take your word for the arithmetic, but how does that combination make for a speed limit?”

“There’s an easy answer you’re not going to like — it’s a speed because the units come out meters per second.”

“That’s a cheat. I don’t like it at all and it doesn’t account for the limit part. Explain it with Physics, no fancy equations.”

“Tough assignment. Okay, typical waves have a displacement force, like wind or something pushing up on an ocean wave, that works against a restoring force, such as gravity pulling down. Electromagnetic waves are different. The electric component supplies the up force, but the magnetic component twists sideways instead of restoring down. The wave travels as a helix. The CE and CM properties determine how tightly it spirals through space. That’s lightspeed.”

“And the limit part?”

“Einstein maintained that anything that happens must follow the same rules for all observers no matter how each is moving. The only way that can be true is if space is subject to the Lorentz contraction √[1-(v/vmax)²] for some universal maximum speed vmax. Maxwell’s electromagnetism equations showed that vmax is c. Okay?”

“I suppose.”

~ Rich Olcott

  • * Vinnie hates equations even with regular letters, Greek letters make it worse. Hence my using CE and CM instead of the conventional ε0 and μ0 notation. Sue me.

Squaring The Circle

On By rolcottIn Cosmology, UncategorizedLeave a comment

Vinnie gives me the eye. “That crazy theory of yours is SO bogus, Sy, and there’s a coupla things you said we ain’t heard before.”

“What’s wrong with my Mach’s Principle of Time?”

“If the rest of the Universe is squirting one thing forward along Time, then everything’s squirting everything forward. No push‑back in the other direction. You might as well say that everything’s running away from the Big Bang.”

“That’s probably a better explanation. What are the couple of things?”

“One of them was, ‘geodesic,‘ as in ‘motion along a geodesic.‘ What’s a geodesic?”

“The shortest path between two points.”

“That’s a straight line, Mr Moire. First day in Geometry class.”

“True in Euclid’s era, Jeremy, but things have moved on since then. These days the phrase ‘shortest path’ defines ‘straight line’ rather than the other way around. Furthermore, the choice depends on how you define ‘shortest’. In Minkowski’s spacetime, for instance, do you mean ‘least distance’ or ‘least interval’?”

“How are those different?”

“The word ‘distance’ is a space‑only measurement. Minkowski plotted space in x,y,z terms just like Newton would have if he could’ve brought himself to use René Descartes’ cartesian coordinates. You know Euclid’s a²+b²=c² so you should have no problem calculating 3D distance as d=√(x²+y²+z²).”

“That makes sense. So what’s ‘interval’ about then?”

“Time has entered the picture. In Minkowski’s framework you handle two ‘events’ that may be at different locations and different times by using what he called the ‘interval,’ s. It measures the path between events as
s=√[(x²+y²+z²)–(ct)²]. Usually we avoid the square root sign and work with s².”

“That minus sign looks weird. Where’d it come from?”

“When Minkowski was designing his spacetime, he needed a time scale that could be combined with the x,y,z lengths but was perpendicular to each of them. Multiplying time by lightspeed c gave a length, but it wasn’t perpendicular. He could get that if he multiplied by i=√(–1) to get cti as a partner for x,y,z. Fortunately, that forced the minus sign into the sum‑of‑squares
(x²+y²+z²)–(ct)² formula.”

Vinnie’s getting impatient. “What is an actual geodesic, who cares about them, and what do these equations have to do with anything?”

“A geodesic is a path in spacetime. Light always travels along a geodesic. The modern version of Newton’s First Law says that any object not subject to an outside force travels along a geodesic. By definition the geodesic is the shortest path, but you can’t select which path from A to B is the shortest unless you can measure or calculate them. There’s math to tell us how to do that. Time’s a given in a Newtonian Universe, not a coordinate, so geodesics are distance‑only. We calculate d along paths that Euclid would recognize as straight lines. That’s why the First Law is usually stated in terms of straight lines.”

“So the lines can go all curvy?”

“Depends, Vinnie. When you’re piloting an over‑water flight, you fly a steady bearing, right?”

“Whenever ATC and the weather lets me. It’s the shortest route.”

“So according to your instruments you’re flying a straight line. But if someone were tracking you from the ISS they’d say you’re flying along a Great Circle, the intersection of Earth’s surface with some planar surface. You prefer Great Circles because they’re shortest‑distance routes. That makes them geodesics for travel on a planetary surface. Each Circle’s a curve when viewed from off the surface.”

“Back to that minus sign, Mr Moire. Why was it fortunate?”

“It’s at the heart of Relativity Theory. The expression links space and time in opposite senses. It’s why space compression always comes along with time dilation.”

“Oh, like at an Event Horizon. Wait, can’t that s²=(x²+y²+z²)–(ct)² arithmetic come out zero or even negative? What would those even mean?”

“The theory covers all three possibilities. If the sum is zero, then the distance between the two events exactly matches the time it would take light to travel between them. If the sum is positive the way I’ve written it then we say the geodesic is ‘spacelike’ because the distance exceeds light’s travel time. If it’s negative we’ve got a ‘timelike’ geodesic; A could signal B with time to spare.”

~ Rich Olcott

The Time Is Out of Joint

On By rolcottIn Cosmology, Crazy Theories, UncategorizedLeave a comment

Vinnie galumphs over to our table. “Hi, guys. Hey, Sy, I just read your Confluence post. I thought that we gave up on things happening simultaneous because of Einstein and relativity but I guess that wasn’t the reason.”

“Oh, things do happen simultaneously, no‑one claims they don’t, it’s just that it’s impossible for two widely‑separated observers to have evidence that two widely‑separated events happened simultaneously. That’s a very different proposition.”

“Ah, that makes me feel better. The ‘nothing is simultaneous‘ idea was making me itchy ’cause I know for sure that a good juggler lets go with one hand just as they’re catching with the other. How’s Einstein involved then?”

“Lightspeed’s a known constant. Knowing distance and lightspeed lets you calculate between‑event time, right? The key to simultaneity was understanding why lightspeed is a constant. We’d known lightspeed wasn’t infinite within the Solar System since Rømer’s time, but people doubted his number applied everywhere. Maxwell’s theory of electromagnetism derived lightspeed from the properties of space itself so it’s universal. Only in Newton’s Universe was it possible for two distant observers to agree that two also‑distant events were simultaneous.”

“Why was Newton’s Universe special?

“Space held still and didn’t bend. Astronomers A and B had a stable baseline between them. After measuring the baseline with light they could measure the angles each observed between the events. Some trigonometry let them send each other congratulatory messages on seeing a simultaneous pair of incidents. After Einstein’s work, they knew better.”

“It’s frames again, ain’t it?”

“Of course, Vinnie. A‘s frame is almost certainly moving relative to B‘s frame. Motion puts the Lorentz relativity factor into the game, making each astronomer’s clock run faster than the other’s. Worse, each astronomer sees that the other’s yardsticks are too short.”

Jeremy gives me a confused look.

“Space compression goes along with time dilation, Jeremy. Professor Hanneken will explain it all when your class gets to that unit. Bottom line, things can happen simultaneously in Einstein’s Universe, but no‑one can agree on which things.”

“Wait, if every frame has its own time‑rate, how can two spaceships rendezvous for an operation?”

“Good question, Jeremy. Einstein had an answer but complications hide under the covers. He suggested that A start a timer when sending a light pulse to a mirror at B. A waits for the reflection. B starts a timer when they see A‘s pulse. A measures the pulse’s round‑trip time. Each creates a clock that advances one tick for half of the round-trip time. B sets their clock back by one tick. That done, they agree to meet some number of ticks later.”

“Hmm… That should work, but you said there are complications.”

“There are always complications. For instance, suppose B is slingshotting around a black hole so that pulse and reflection travel different pathlengths. Or suppose one frame is rotating edge‑on to the other. In practice the ships would re‑sync repeatedly while approaching the rendezvous point.”

Vinnie erupts. “HAW! Successive approximation again!”

“Indeed. If we could extend the method to more than two participants we’d have a true Universal Coordinated Time.”

“Don’t we have that, Mr Moire? The Big Bang happened 14 billion years ago. Couldn’t we measure time from that?”

“Sort of. Last I looked the number was 13.787 plus‑or‑minus 20 million years. Too much slop for an instantaneous fleet‑level rendezvous like the final battle scene in StarTrek:Picard. But you’ve brought up an interesting question for a Crazy Theories seminar. One of Cosmology’s deepest unsolved questions is, ‘How does inertia work?’ Do you remember Newton’s First Law?”

<closes eyes> “In an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.“

“Right. In other words, every object resists change to its current steady motion along a geodesic. Why is that? There’s no coherent, well‑founded, well‑tested theory. Einstein liked Mach’s Principle, which says inertia exists because every object is attracted through space to all the mass in the Universe. Suppose there’s a Mach’s Principle for Time, saying that objects squirt up the Time axis because they’re repelled by all the mass in the Universe.”

Vinnie hoots, “Bo-o-o-ohh-GUS!”

~ Rich Olcott

Sussing Out The Unseeable

On By rolcottIn Astronomy: Techniques, Cosmology, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“Hello, Mr Moire.”

“Afternoon, Walt. Pizza time again?”

“No, too public. Poor craft to be seen too often in the same place. There’s a park bench by the lake.”

“I know the spot.”

“Fifteen minutes.”

“Twenty.”

“Afternoon, Walt. What are your people curious about this time?”

“Word is that astronomers uncovered a huge amount of matter they’d been searching for. We’re interested in concealment techniques, so we want to know how it was hidden and how was it found.”

“Forty percent of all baryonic matter—”

“Baryonic?”

“Made out of atoms. Baryons are multi-quark particles like protons and—”

“Leave the weeds and get back to the topic. Where was that 40% hiding?”

“In plain sight, all over the sky, in strands forming a network that connects galaxies and galaxy clusters. They’re calling it the Cosmic Web.”

“Something that big … how was hidden?”

“Some techniques I’m sure you’ll recognize. First, the material in the strands is diffuse — just an atom or two per cubic meter. An Earth laboratory would be proud to pump down a vacuum ten million times more dense.”

<taking notes> “Spread your forces so there’s no prime target for counter‑attack, mm‑hm. But if the material’s that thin, surely it doesn’t mass much.”

“Remember how big space is. These filaments span the widths of multiple galaxies. Do the math. A thread could be on the order of 100 million lightyears long by 1000 lightyears in diameter. A lightyear is 1016 meters. The thread has a volume of about 1062 cubic meters. At 10-26 kilogram per cubic meter that’s 1036 kilograms which is comparable to the mass of a small galaxy. That’s just one thread. Add them up and you get roughly half the baryons in the Universe, all hiding in the Web.”

“Concealment by dispersal, got it. What’s another technique?”

“Camouflage. No, not tiny uniforms in a woodland pattern. These atoms fade into the background because oncoming light waves pass right by them unless the wave has exactly the right wavelength for an absorption.”

“So how did astronomers detect these scattered and camouflaged atoms?”

“A couple of different ways. X‑rays, for one.”

“But these atoms are camouflaged against passing light. X‑rays are light waves.”

“X‑rays the atoms emit. Everybody thinks that space is cold, but those lonely atoms bounce around with a kinetic energy equivalent to million‑degree temperatures. When two of them collide some of that kinetic energy escapes as high‑frequency light, X‑ray range. Not a whole lot, because the atoms are sparse, but enough that European and Japanese space telescopes were able to tweeze it out of the background.”

“Use sensitive mics to pick up whispered convo in the opposing line.”

<pause> “Right, more or less. What do you know about refraction?”

“Mmm… Newton and his prism, splitting white light into different colors. I’ve no idea how that works.”

“The short answer is that the speed of light depends on its wavelength and the medium it’s traversing. In a perfect vacuum, light always goes at top speed just like Einstein said, but charged particles in its path slow it down.”

“Even those atoms in space that you said can’t absorb light?”

“Yup. It’s called virtual coupling; quantum’s involved. One inaccurate way to describe the interaction is that atoms occasionally absorb wrong‑wavelength photons but spit them right back out again after a brief delay. Short wavelengths see more of that effect than long wavelengths do. With me?”

<pause> “Go on.”

“Does the phrase ‘Fast Radio Burst’ sound familiar?”

“Of course, but probably not the way you mean.”

“Ah. Right. For this context, Fast Radio Bursts are isolated pulses of radio‑frequency light from incredibly bright extra-galactic sources we don’t understand. They’re all over the sky. A pulse lasts only a millisecond or so. What’s important here is that refraction skews each pulse’s wavelength profile as it travels through the intergalactic medium. Researchers analyze the distortions to detect and characterize Web filaments in the direction each pulse came from.”

“Intercept the oppo’s communications to the front.”

“That’s about the size of it.”

“Bye.”

“Don’t mention it.”

The Cosmic Web
Visualization: Frank Summers (STScI); Simulation: Martin White and Lars Hernquist, Harvard University

~ Rich Olcott

A Carefully Plotted Tale

On By rolcottIn Cosmology, Physics: Quantum Mechanics, UncategorizedLeave a comment

<chirp, chirp> “Moire here.”

“Hello, Mr Moire. Remember me?”

“Yes, I do, Walt. I hope your people were satisfied with what you brought them from our last meeting.”

“They were, which is why I’m calling. Buy you pizza at Eddie’s, fifteen minutes?”

“Make it twenty.”

We’re at the rear‑corner table, Walt facing both doors, naturally. “So, what’s the mysterious question this time?”

“Word on the street is that the CPT Law’s being violated. We want to know who’s involved, and what’s their connection with ChatGPT.”

Good thing I’ve just bit into my pizza so I can muffle my chuckle in my chewing. “What do you know about anti‑matter?”

“Inside‑out atoms — protons outside whizzing around electrons in the nucleus.”

“Common misconception. One proton has the mass of 1800 electrons. An atom built as you described would be unstable — the thing would fly apart. You’ve got anti‑matter’s charges arranged right but not the particles. Anti‑matter has negative anti‑protons in the nucleus and positrons, positive electrons, on the outside.”

<writing rapidly in his notebook> “You can do that? Just flip the sign on a particle?”

“No, positrons and such are respectable particles in their own right, distinct from their anti‑partners. Electric charge comes built into the identity. What’s important is, an anti‑atom behaves exactly like a normal atom does. Maxwell’s Equations and everything derived from them, including quantum mechanics, work equally well for either charge structure.”

“There’s a bit of Zen there — change but no‑change.”

“Nice. Physicists call that sort of thing a symmetry. In this case it’s charge symmetry, often written as C.”

“The C in CPT?”

“Exactly.”

“What about the P and T?”

“When someone says something is symmetrical, what do you think of first?”

“Right side’s a reflection of left side. Symmetrical faces look better but they’re usually less memorable.”

“Interesting choice of example. Anyway, reflection symmetry is important in common physical systems.”

“Classical Greek and Cambodian architecture; the Baroque aesthetic without the decorative frills.”

“I suppose so. Anyway, we call reflection symmetry Parity, or P for short.”

“And T?”

“Time.”

“Time’s not symmetrical. It’s always past‑to‑future.”

“Maybe, maybe not. In all our physical laws that deal with a small number of particles, you can replace t for time with –t and get the same results except for maybe a flipped sign. Newton’s Laws would run the Solar System in reverse just as well as they do forward.”

“But … Ah, ‘small number of particles,’ that’s your out. If your system has a large number of particles, you’re in chaos territory where randomness and entropy have to increase. Entropy increase is the arrow for one‑way time.”

“Good quote.”

“I’ve been in some interesting conversations. You’re not my only Physics source. So CPT is about Charge AND Parity AND Time symmetries. But you can’t simply add them together.”

“You multiply them. Technically, each of them is represented by a mathematical operator—”

“Step away from the technically.”

“Understood. This’ll be simpler. If a system’s atoms have positive nuclei, set C=1, otherwise set C=–1. If the system’s naturally‑driven motion is counterclockwise set P=1, otherwise P=–1. If time is increasing, set T=1, otherwise set T=–1. Okay?”

“Go on.”

“You can summarize any system’s CPT state by multiplying the prevailing symmetry values. The product will be either +1 or –1. The CPT Law says that in any universe where quantum mechanics and relativity work, one CPT state must hold universe‑wide.”

“Make it real for me.”

“You know the Right-hand Rule for electromagnetism?”

“Grab the wire with your right hand, thumb pointing along the current. Your fingers wrap in the direction of the spiraling magnetic field.”

“Perfect. Suppose C*P*T=+1 for this case. Now reverse the charge, making C=–1. What happens?”

“Ssss… The magnetic spin flips orientation. That’s a reflection operation so P=–1. The C*P*T calculation is (+1)*(–1)*(–1)=+1, no change.”

“The CPT Law in action. The CPT violation you’ve heard about is only observed in rare weak‑force‑mediated radioactive decays of a carefully prepared nucleus. That was a 1956 Nobel‑winning discovery, though the right person didn’t win it.”

“1956. Decades before A.I.”

“Yup, ChatGPT is off the hook. For that.”

“Bye.”

“Don’t mention it.”

~ Rich Olcott

  • Thanks to Caitlin, the hand model.

Why A Disk?

On By rolcottIn Astronomy: Stellar Science, Cosmology, UncategorizedLeave a comment

Late Summer is quiet time on campus and in my office. Too quiet. I head over to Cal’s coffee shop in search of company. “Morning, Cal.”

“Morning, Sy. Sure am glad to see you. There’s no‑one else around.”

“So I see. No scones in the rack?”

“Not enough traffic yet to justify firing up the oven on such a hot day. How about a biscotti instead?”

“If it’s only the one it’s a biscotto. Pizza Eddie’s very firm on that. Yeah, I’ll have one.”

“Always learning. By the way, a photo spread in one of my astronomy magazines got me thinking. How come there’s so much flat out there?”

“Huh? I know you’re not one of those flat‑Earthers.”

“Not the planets, I mean the way their orbits go all in the same plane. Same for most of the asteroids and the Kuiper belt, even. Our Milky Way galaxy’s basically flat, too, and so are a lot of the others. Black hole accretion disks are flat. You’d think if some baby star or galaxy was attracting stuff from everywhere to grow itself, the incoming would make a big globe. But it’s not, we get flatness. How come?”

“Bad aim and angular momentum.”

“What’s aim got to do with it?”

“Suppose there’s only two objects in the Universe and they’re closing in on each other. If they’re aimed dead‑center to each other, what happens?”

“CaaaRUNCH!!!”

“Right. Now what if the aim’s off so they don’t quite touch?”

“Oh, I know that one … it’ll come to me … yeah, Roche’s limit, it was in an article a few months ago. Whichever’s less dense will break up and all the pieces go like Saturn’s rings. Which are also flat, by the way.”

“In orbit around the survivor, mm‑hm. The pieces can’t fall straight down because they still have angular momentum.”

“I know about momentum like when you crash a car if you go too fast for your brakes. Heavier car or faster speed, you get a worse crash. How does angle fit into that — bigger angle, more angular momentum?”

“Not quite. In general, momentum is mass multiplied by speed. It’s a measure of the force required to stop something or at least slow it down. You’ve described linear momentum, where ‘speed’ is straight‑line distance per time. If you’re moving along a curve, ‘speed’ is arc‑length per time.”

“Arc‑length?”

“Distance around part of a circle. Arc‑length is angle in radians, multiplied by the circle’s radius. If you zip halfway around a big circle in the same time it took me to go halfway around a small circle, you’ve got more angular momentum than I do and it’d take more force to stop you. Make sense?”

“What if it’s not a circle? The planet orbits are all ellipses.”

“It’s still arc‑length except that you need calculus to figure it. That’s why Newton and Leibniz invented their methods. A falling something that misses a gravity center keeps falling but on an orbit. Whatever momentum it has acts as angular momentum relative to that center. There’s no falling any further in without banging into something else coming the other way and each object canceling the other’s momentum.”

“Or burning fuel if it’s a spaceship.”

“… Right. … So anyway, suppose you’ve got a star or something initially surrounded by a spherical cloud of space junk whirling around in all different orbits. What’s going to happen?”

“Lots of banging and momentum canceling until everything’s swirling more‑or‑less in the same direction and closer in than at come‑together time. But it’s still a ball.”

“Gravity’s not done. Think about northern debris. It’s attracted to the center, but it’s also attracted to the southern debris and vice-versa. They’ll meet midway and build a disk. The ball‑to‑disk collapse isn’t even opposed by angular momentum. Material at high latitudes, north and south, can lose gravitational potential energy by dropping straight in toward the equator and still be at the orbitally correct distance from the axis of rotation.”

“That’d work for stuff collecting around a planet, wouldn’t it?”

“It’d even work for stuff collecting around nothing, just a clump in a random density field. That may be how stars are born. Collapsing’s the hard part.”

~ Rich Olcott

Two’s Company, Three Is Perturbing

On By rolcottIn Mathematics, Physics: Newton and Gravity, Space Travel, UncategorizedLeave a comment

Vinnie does this thing when he’s near the end of his meal. He mashes his pizza crumbs and mozzarella dribbles into marbles he rolls around on his plate. Mostly on his plate. Eddie hates it when one escapes onto his floor. “Vinnie, you lose one more of those, you’ll be paying extra.”

“Aw, c’mon, Eddie, I’m your best customer.”

“Maybe, but there’ll be a surcharge for havin’ to mop extra around your table.”

Always the compromiser, I break in. “How about you put on less sauce, Eddie?”

Both give me looks you wouldn’t want.
  ”Lower the quality of my product??!?”
    ”Adjust perfection??!?”

“Looks like we’ve got a three‑body problem here.” Blank looks all around. “You two were just about to go at it until I put in my piece and suddenly you’re on the same side. Two‑way interaction predictable results, three‑way interaction hard to figure. Like when Newton calculated celestial orbits to confirm his Laws of Gravity and Motion. They worked fine for the Earth going around the Sun, not so good for the Moon going around the Earth. The Sun pulls on the Moon just enough to play hob with his two‑body Earth‑Moon predictions.”

“Newton again. So how did he solve it?”

“He didn’t, not exactly anyway.”

“Not smart enough?”

“No, Eddie, plenty smart. Later mathematicians have proven that the three‑body problem simply doesn’t have a general exact solution.”

“Ah-hah, Sy, I heard weaseling — general?”

“Alright, Vinnie, there are some stable special cases. Three bodies at relative rest in an equilateral triangle; certain straight‑line configurations; two biggies circling each other and a third, smaller one in a distant orbit around the other two’s center of gravity. There are other specials but none stable in the sense that they wouldn’t be disrupted by a wobbly gravity field from a nearby star or the host galaxy.”

A special-case solution
to the three-body problem
by MaxwellMolecule,
licensed under CC ASA 4.0

“So if NASA’s mission planners are looking at a four‑body Sun‑Jupiter‑Europa‑Juno situation, what’re they gonna do? ‘Give up’ ain’t an option.”

“Sure not. There’s a grand strategy with variations. The oldest variation goes back to before the Egyptian builders and everybody still uses it. Vinnie, when you fly a client to Tokyo, do you target a specific landing runway?”

“Naw, I aim for Japan, contact ATC Narita when I get close and they vector me in to wherever they want me to land.”

“How about you, Eddie? How do you get that exquisite balance in your flavoring?”

“Ain’t easy, Sy. Every batch of each herb is different — when it was picked, how it was stored, even the weather while it was growing. I start with an average mix which is usually close, then add a pinch of this and a little of that until it’s right.”

“For both of you, the critical word there was ‘close’. Call it in‑flight course adjustments, call it pinch‑and‑taste, everybody uses the ‘tweaking’ strategy. It’s a matter of skill and intuition, usually hard to generalize and even harder to teach in a systematic fashion. Engineers do it a lot, theoretical physicists work hard to avoid it.”

“What’ve they got that’s better?”

” ‘Better’ depends on your criteria. The method’s called ‘perturbation theory’ and strictly speaking, you can only use it for certain kinds of problems. Newton’s, for instance.”

“Good ol’ Newton.”

“Of course. Newton’s calculations almost matched Kepler’s planetary observations, but finagling the ‘not quite’ gave Newton headaches. More than 150 years passed before Laplace and others figured out how to treat a distant object as a perturbation of an ideal two‑body situation. It starts with calculating the system’s total energy, which wasn’t properly defined in Newton’s day. A perturbation factor p controls the third body’s contribution. The energy expression lets you calculate the orbits, but they’re the sum of terms containing powers of p. If p=0.1, p2=0.01, p3=0.001 and so on. If p isn’t zero but is still small enough, the p3 term and maybe even the p2 term are too small to bother with.”

“I’ll stick with pinch‑and‑taste.”

“Me and NASA’ll keep course‑correcting.”

~ Rich Olcott

Why Those Curtains Ripple

On By rolcottIn Astronomy: Planetary Science, Physics: Electromagnetism, UncategorizedLeave a comment

I’m in the scone line at Cal’s Coffee when suddenly there’s a too‑familiar poke at my back, a bit right of the spine and just below the shoulder blade. I don’t look around. “Morning, Cathleen.”

“Morning, Sy. Your niece Teena certainly likes auroras, doesn’t she?”

“She likes everything. She’s the embodiment of ‘unquenchable enthusiasm.’ At that age she’s allowed.”

“It’s a gift at any age. Some of the kids in my classes, they just can’t see the wonders no matter how I try. I show them aurora photos and they say, ‘Oh yes, red and green in the sky‘ and go back to their phone screens. Of course there’s no way to get them outside late at night at a location with minimal light pollution.”

“I feel your pain.”

“Thanks. By the way, your aurora write-ups have been all about Earth’s end of the magnetic show. When you you going to do the rest of the story?”

“How do you mean?”

“Magnetism on the Sun, how a CME works, that sort of thing.”

“As a physicist I know a lot about magnetism, but you’re going to have to educate me on the astronomy.”

Plane‑polarized Lorentz (electromagnetic) wave
 Electric (E) component is red
 Magnetic (B) component is blue
(Image by Loo Kang Wee and Fu-Kwun Hwang from Wikimedia Commons)
Licensed under CC ASA3.0 Unported

“Deal. You go first.”

<displaying an animation on Old Reliable> “We’ll have to flip between microscopic and macroscopic a couple times. Here’s the ultimate micro — a single charged particle bouncing up and down somewhere far away has generated this Lorentz‑force wave traveling all alone in the Universe. The force has two components, electric and magnetic, that travel together. Neither component does a thing until the wave encounters another charged particle.”

“An electron, right?”

“Could be but doesn’t have to be. All the electric component cares about is how much charge the particle’s carrying. The magnetic component cares about that and also about its speed and direction. Say the Lorentz wave is traveling east. The magnetic component reaches out perpendicular, to the north and south. If the particle’s headed in exactly the same direction, there’s no interaction. Any other direction, though, the particle’s forced to swerve perpendicular to both the field and the original travel. Its path twists up- or downward.”

A charged particle traversing a Lorentz wave

“But if the particle swerves, won’t it keep swerving?”

“Absolutely. The particle follows a helical path until the wave gives out or a stronger field comes along.”

“Wait. If a Lorentz wave redirects charge motion and moving charges generate Lorentz waves, then a swerved particle ought to mess up the original wave.”

“True. It’s complicated. You can simplify the problem by stepping back far enough that you don’t see individual particles any more and the whole assembly looks like a simple fluid. We’ve known for centuries how to do Physics with water and such. Newton invented hydrodynamics while battling the ghost of Descartes to prove that the Solar System’s motion was governed by gravity, not vortices in an interplanetary fluid. People had tried using Newton‑style hydrodynamics math to understand plasma phenomena but it didn’t work.”

<grinning> “I don’t imagine it would — all that twistiness would have thrown things for a loop.”

“Haha. Well, in the early 1940s Swedish physicist Hannes Alfven started developing ideas and techniques, extending hydrodynamics to cover systems containing charged particles. Their micro‑level electromagnetic interactions have macro‑level effects.”

“Like what?”

“Those aurora curtains up there. Alfven showed that in a magnetic field plasmas can self‑organize into what he called ‘double layers’, pairs of wide, thin sheets with positive particles on one side against negative particles in the other. Neither sheet is stable on its own but the paired‑up structure can persist. Better yet, plasma magnetic fields can support coherent waves like the ones making that curtain ripple.”

“Any plasma?”

“Sure.”

“Most of the astronomical objects I show my students are associated with plasmas — the stars themselves, of course, but also the planetary nebulae that survive nova explosions, the interstellar medium in galactic star‑forming regions, the Solar wind, CMEs…”

“Alfven said we can’t understand the Universe unless we understand magnetic fields and electric currents.”

~ Rich Olcott