Tag: Newton

A Play Beyond The Play

On By rolcottIn Cosmology, Gravitational astronomy, Uncategorized, Vera RubinLeave a comment

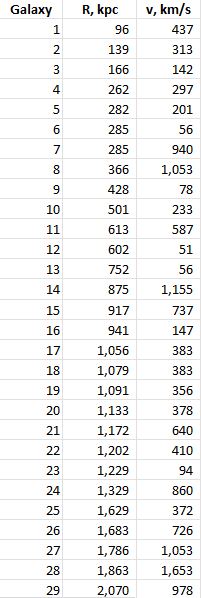
Vinnie takes a long thoughtful look at the image that had dashed his beautiful six‑universe idea. “Wait, Sy. I don’t like this picture”

“Because it messes up your invention?”

“No, because how can they know what that halo looks like? I mean, the whole thing with dark matter is that we can’t see it.”

“You’re right about that. Dark matter’s so transparent that even with five times more mass than normal matter, it doesn’t block CMB photons coming from 13.8 billion lightyears away. That still boggles my brain every once in a while. But dark matter’s gravitational effects — those we can see.”

“Yeah, I remember a long time ago we talked about Fritz Zwicky and Vera Rubin and how they told people about galaxies held together by too much gravity but nobody believed them.”

“Well, they did, after a while—”

“A long while, like a long while since those talks. Remind me what ‘too much gravity’ was about.”

“It was about conflicts between their observations and the prevailing theoretical models. Everyone thought that galaxies and galaxy clusters should operate pretty much like planetary orbits — your speed increases the closer you are to the center, up to Einstein’s speed limit. Newton’s Laws of Motion predict how fast you should move if you’re at a certain distance from a body with a certain mass. If you’re moving faster than that, you fly away.”

“Yeah, escape velocity. So the galaxies in Zwicky’s cluster didn’t follow Newton’s Laws?”

“They didn’t seem to. Galaxies that should have escaped were still in there. The only way he could explain the stability was to suppose the galaxies are only a small fraction of the cluster’s mass. Extra gravity from the extra mass must bind things together. Forty years later Rubin’s improved technology revealed that stars within galaxies had the same anomalous motion.”

“I’m guessing the ‘faster near the center’ rule didn’t hold, or else you wouldn’t be telling this story. Spun like a wheel, I bet.”

“When a wheel spins, every part of it rotates at the same angular speed, the same number of degrees per second, right?”

“Ahh, the bigger my circle the higher my airspeed so the rule would be ‘faster farther out’.”

“That’s the wheel rule, right, but Rubin’s data showed that stars within galaxies don’t obey that one either. She measured lots of stars in Andromeda and other galaxies. Their linear speeds, kilometers per second, are nearly identical from near the center all the way out. Even dust and gas clouds beyond the galactic starry edges also fit the ‘same linear speed everywhere’ rule. You’d lose the bet.”

“That just doesn’t feel right. How can just gravity make that happen?”

“It can if the right amount of dark matter’s distributed in the right‑shaped smeared‑out hollowed‑out spherical halo. The halo’s radial density profile looks about like this. Of course, profiles for different galaxies differ in spread‑outness and other details, but the models are pretty consistent.”

“Wait, if dark matter only does gravity like you said, why’s that hole in the middle? Why doesn’t everything just fall inward?”

“Dark matter has mass so it also has inertia, momentum and angular momentum, just as normal matter does. Suppose some of the dark matter has collected gravitationally into a blob and the blob is moving slower than escape velocity. If it’s flying straight at the center of gravity it’ll get there and stay there, more or less. But if the blob’s aimed in any other direction, it has angular momentum relative to the center. Momentum’s conserved for dark matter, too. The blob eventually goes into orbit and winds up as part of the shell.”

“Does Zwicky’s galaxy cluster have a halo, too?”

“Not in the same way. Each galaxy probably has its own halo but the galaxies are far apart relative to their size. The theoreticians have burned huge amounts of computer time simulating the chaos inside large ensembles of gravity‑driven blobs. I just read one paper about a 4‑billion‑particle calculation and mind you, a ‘particle’ in this study carried more than a million solar masses. Big halos host subhalos, with filaments of minihalos tying them together. What we can’t see is complicated, too.”

~ Rich Olcott

Hiding Under Many Guises

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized3 Comments

Vinnie lifts his pizza slice and pauses. “I dunno, Sy, this Pressure‑Volume part of enthalpy, how is it energy so you can just add or subtract it from the thermal and chemical kinds?”

“Fair question, Vinnie. It stumped scientists through the end of Napoleon’s day until Sadi Carnot bridged the gap by inventing thermodynamics.”

“Sounds like a big deal from the way you said that.”

“Oh, it was. But first let’s clear the ‘is it energy?’ question. How would Newton have calculated the work you did lifting that slice?”

“How much force I used times the distance it moved.”

“Putting units to that, it’d be force in newtons times distance in meters. A newton is one kilogram accelerated by one meter per second each second so your force‑distance work there is measured in kilograms times meters‑squared divided by seconds‑squared. With me?”

“Hold on — ‘per second each second’ turned into ‘per second‑squared.” <pause> “Okay, go on.”

“What’s Einstein’s famous equation?”

“Easy, E=mc².”

“Mm-hm. Putting units to that, c is in meters per second, so energy is kilograms times meters‑squared divided by seconds‑squared. Sound familiar?”

“Any time I’ve got that combination I’ve got energy?”

“Mostly. Here’s another example — a piston under pressure. Pressure is force per unit area. The piston’s area is in square meters so the force it feels is newtons per meter‑squared, times square meters, or just newtons. The piston travels some distance so you’ve got newtons times meters.”

“That’s force‑distance work units so it’s energy, too.”

“Right. Now break it down another way. When the piston travels that distance, the piston’s area sweeps through a volume measured in meters‑cubed, right?”

“You’re gonna say pressure times volume gives me the same units as energy?”

“Work it out. Here’s a paper napkin.”

“Dang, I hate equations … Hey, sure enough, it boils down to kilograms times meters‑squared divided by seconds‑squared again!”

“There you go. One more. The Ideal Gas Law is real simple equation —”

“Gaah, equations!”

“Bear with me, it’s just PV=nRT.”

“Is that the same PV so it’s energy again?”

“Sure is. The n measures the amount of some gas, could be in grams or whatever. The R, called the Gas Constant, is there to make the units come out right. T‘s the absolute temperature. Point is, this equation gives us the basis for enthalpy’s chemical+PV+thermal arithmetic.”

“And that’s where this Carnot guy comes in.”

“Carnot and a host of other physicists. Boyle, Gay‑Lussac, Avagadro and others contributed to Clapeyron’s gas law. Carnot’s 1824 book tied the gas narrative to the energetics narrative that Descartes, Leibniz, Newton and such had been working on. Carnot did it with an Einstein‑style thought experiment — an imaginary perfect engine.”

“Anything perfect is imaginary, I know that much. How’s it supposed to work?”

<sketching on another paper napkin> “Here’s the general idea. There’s a sealed cylinder in the middle containing a piston that can move vertically. Above the piston there’s what Carnot called ‘a working body,’ which could be anything that expands and contracts with temperature.”

“Steam, huh?”

“Could be, or alcohol vapor or a big lump of iron, whatever. Carnot’s argument was so general that the composition doesn’t matter. Below the piston there’s a mechanism to transfer power from or to the piston. Then we’ve got a heat source and a heat sink, each of which can be connected to the cylinder or not.”

“Looks straight‑forward.”

“These days, sure. Not in 1824. Carnot’s gadget operates in four phases. In generator mode the working body starts in a contracted state connected to the hot Th source. The body expands, yielding PV energy. In phase 2, the body continues to expand while it while it stays at Th. Phase 3, switch to the cold Tc heat sink. That cools the body so it contracts and absorbs PV energy. Phase 4 compresses the body to heat it back to Th, completing the cycle.”

“How did he keep the phases separate?”

“Only conceptually. In real life Phases 1 and 2 would occur simultaneously. Carnot’s crucial contribution was to treat them separately and yet demonstrate how they’re related. Unfortunately, he died of scarlet fever before Clapeyron and Clausius publicized and completed his work.”

~ Rich Olcott

Energy Is A Shape-shifter

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Another dinner, another pizza at Eddie’s place. Vinnie wanders over to my table. “Hi, Sy, got a minute?”

“Not doing anything other than eating, Vinnie. What’s on your mind other than the sound of my chewing?”

“At least you keep your mouth closed. No, it’s about this energy thing you’ve gotten back into. I read that enthalpy piece and it’s bothering me.”

“In what way?”

“Well, you said that something’s enthalpy is the energy total of ‘thermal plus Pressure‑Volume plus chemical energy,’ right? I’m trying to fit that together with the potential energy and kinetic energy we talked about a while ago. It’s not working.”

“Deep question for dinner time but worth the effort. Would it help if I told you that the ‘actual versus potential’ notion goes back to Aristotle, the ‘kinetic’ idea came from Newton’s enemy Leibniz, but ‘enthalpy’ wasn’t a word until the 20th century?”

“Not a bit.”

“Didn’t think it would. Here’s another way to look at it. The thinkers prior to the mid‑1700s all looked at lumpy matter — pendulums, rolling balls on a ramp, planets, missiles — either alone or floating in space or colliding with each other. You could in principle calculate kinetic and potential energy for each lump, but that wasn’t enough when the Industrial Revolution came along.”

“What more did they want?”

“Fuel was suddenly for more than cooking and heating the house. Before then, all you needed to know was whether the log pile was stocked better than it was last year. If not, you might have a few chilly early Spring days but you could get past that. Then the Revolution came along. Miners loved Watt’s coal‑fired water‑pump except if you bought one and ran out of coal then the mine flooded. The miners learned that some kinds of coal burned hotter than others. You didn’t need as much of the good kind for a day’s pumping. The demand for a coal‑rating system got the scientists interested, but those lumps of coal weren’t falling or colliding, they just sat there with their heat locked inside. The classical energy quantities didn’t seem to apply so it was time to invent a new kind of energy.”

“That’s how Conservation of Energy works? You just spread the definition out a little?”

“That’s the current status of dark energy, for instance. We know the galaxies are moving apart against gravity so dark energy’s in there to balance the books. We have no good idea why it exists or where it comes from, but we can calculate it. ‘Internal energy’ put the Victorian‑era physicists in the same pickle — ‘atom’ and ‘molecule’ were notions from Greek and Roman times but none of the Victorians seriously believed in them. The notion of chemical bond energy didn’t crop up until the twentieth century. Lacking a good theory, all the Victorians could do was measure and tabulate heat output from different chemical reactions, the data that went into handbooks like the CRC. Naturally they had to invent thermodynamics for doing the energy accountancy.”

“But if it’s just book-balancing, how do you know the energy is real?”

“Because all the different forms of energy convert to each other. Think of a rocket going up to meet the ISS. Some of the rocket fuel’s chemical energy goes into giving the craft gravitational potential energy just getting it up there. At the same time, most of the chemical energy becomes kinetic energy as the craft reaches the 27600 km/h speed it needs to orbit at that altitude.”

<grin> “All?”

“Okay, we haven’t figured out how to harness dark energy. Yet.”

“HAW! Wait, how does enthalpy’s ‘chemical+PV+thermal’ work when the pressure’s zero, like out in space?”

“Then no work was done against an atmosphere up there to make way for the volume. Suppose you suddenly transported a jug of fuel from Earth up to just outside of the ISS. Same amount of fuel, so same amount of chemical energy, right? Same temperature so same thermal component?”

“I suppose.”

“The volume that the jug had occupied on Earth, what happened to it?”

“Suddenly closed in, probably with a little thud.”

“The thud sound’s where the Earth‑side PV energy went. It all balances out.”

~ Rich Olcott

New (Old) Word: Frigorific!

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

A quiet morning at Cal’s Coffee. I’m sipping my morning mud when Susan Kim bustles to my table, mocha latte in hand. “There you are, Sy. I loved your posts in tribute to the well‑thumbed copy of the CRC Handbook on my desk.”

“Glad you enjoyed them.”

“Your Rumford stuff made it even better because I did a class report on him once so I caught your ‘frigorific‘ reference. What do you know about the background to that?”

“Not much. Didn’t sound like a real word when I ran across it.”

“Oh, it’s a real word but it has a technical meaning now that it didn’t in Newton’s time. Back then it was only about making something cold. These days we also use the word for a mixture that maintains a dependable cold temperature. Liquid water and ice, for instance, stays at 0°C as long as there’s still ice in the cold bath. I used to use an ammonium chloride/water frigorific when I needed something down around -15°C. Now of course I use a benchtop refrigerator.”

“Rumford would have liked that. What were the ‘frigorific rays‘ he got all excited about?”

“Long story but there’s a couple of fun twists. Background first. At the end of the 1700s there was a <grin> heated debate about heat. The phlogiston theory was dead by that time but people still liked the idea that heat was a material fluid. It addressed some chemical puzzles but heat transmission was still mysterious. Everyone knew that a hot object gives off heat by radiation, that the radiation travels in straight lines and that it’s reflected by metal mirrors.”

“Right, the Greeks are supposed to have used huge sun‑focusing mirrors to burn up attacking Roman ships.”

“Maybe. Anyhow, those properties connected heat with light. However, a pane of glass blocks radiated heat, at least until the glass gets hot. People argued this meant heat and light weren’t connected. About 1790 a group of physicists loosely associated with the Academy of Geneva dove into the fray. Rumford was in the group, along with Prévost, Saussure and his student Pictet. They had lots of fun with heat theories and experiments. One of Pictet’s experiments lit Rumford’s fire, so to speak.”

“Good one.”

<smile> “It’s a fairly simple setup that a high school science teacher could do. Pictet hung a concave metallic mirror facing down from the ceiling of a draft‑free room. He placed another concave metallic mirror at floor level immediately beneath it, facing upward. He probably used spherical mirrors which are easy to make, but they could have been elliptical or parabolic sections. Anyhow, he put a thermoscope at the upper mirror’s focal point and a hot object at the lower focal point. Sure enough, the upper focal point got hotter, just as you’d expect.”

“No great surprise, the Greeks would have expected that, too.”

“The surprise happened when he put a cold object in there. The thermoscope’s droplet moved in the cold direction.”

“Wait, like anti‑infrared?”

“That’s the effect. Wave‑theory supporter Rumford took that thought, called it ‘frigorific radiation‘ and ran with it. He constructed a whole thesis around cold waves and heat waves as symmetric partners. He maintained wave intensity, both kinds, increases with temperature difference. Our heat sources are hundreds or thousand of degrees hotter than we are but our cold sources are at most a few dozen degrees colder. By his theory that’s why cold wave phenomena are masked by heat waves.”

“Give me a minute. … Ah, got it. The very meaning of a focal point is that all waves end or start there. A cold object at the sending station emits much less infrared than the warm object did. The thermoscope bulb now gets less than it emits. With less input from below its net energy drops. It chills.”

“Nice, Sy. Now for the other twist. Rumford published his theory in 1805. Herschel had already identified infrared radiation in the Sun’s spectrum in 1800. Two strikes against Herschel, I guess — he was British and he was an astronomer. Continental physicists wouldn’t bother to read his stuff.”

~ Rich Olcott

Rumford’s Boring Story

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Okay, Mr Moire, my grandfather’s engineering handbook has Specific Heat tables because Specific Heat measures molecular wabbling. If he’s got them, though, why’s Enthalpy in the handbook, too?”

“Enthalpy’s not my favorite technical term, Jeremy. It’s wound up in a centuries‑old muddle. Nobody back then had a good, crisp notion of energy. Descartes, Leibniz, Newton and a host of German engineers and aristocratic French hobby physicists all recognized that something made motion happen but everyone had their own take on what that was and how to calculate its effects. They used a slew of terms like vis viva, ‘quantity of motion,’ ‘driving force,’ ‘quantity of work,’ a couple of different definitions of ‘momentum‘ — it was a mess. It didn’t help that a lot of the argument went on before Euler’s algebraic notations were widely adopted; technical arguments without math are cumbersome and can get vague and ambiguous. Lots of lovely theories but none of them worked all that well in the real world.”

“Isn’t that usually what happens? I always have problems in the labs.”

“You’re not alone. Centuries ago, Newton’s Laws of Motion and Gravity made good predictions for planets, not so good for artillery trajectories. Gunners always had to throw in correction factors because their missiles fell short. Massachusetts‑born Benjamin Thompson, himself an artilleryman, found part of the reason.”

“Should I know that name?”

“In later years he became Count Rumford. One of those people who get itchy if they’re not creating something. He was particularly interested in heat — how to trap it and how to make it go where you want.”

“Wait, he was an American but he was a Count? I thought that was illegal.”

“Oh, he left the States before they were the States. During the Revolution he organized a Royalist militia in New York and then lit out for Europe. The Bavarians made him a Count after he spent half‑a‑dozen years doing creative things like reorganizing their army, building public works and introducing potato farming. He concocted a nourishing soup for the poor and invented the soup line for serving it up. But all this time his mind was on a then‑central topic of Physics — what is heat?”

“That was the late 1700s? When everyone said heat was some sort of fluid they called ‘caloric‘?”

“Not everyone, and in fact there were competing theories about caloric — an early version of the particle‑versus‑wave controversy. For a while Rumford even supported the notion that ‘frigorific’ radiation transmitted cold the same way that caloric rays transmitted heat. Whatever, his important contributions were more practical and experimental than theoretical. His redesign of the common fireplace was such an improvement that it took first England and then Europe by storm. Long‑term, though, we remember him for a side observation that he didn’t think important enough to measure properly.”

“Something to do with heat, I’ll bet.”

“Of course. As a wave theory guy, Rumford stood firmly against the ‘caloric is a fluid‘ camp. ‘If heat is material,‘ he reasoned, ‘then a heat‑generating process must eventually run out of caloric.’ He challenged that notion by drilling out a cannon barrel while it was immersed in cold water. A couple of hours of steady grinding brought the water up to boiling. The heating was steady, too, and apparently ‘inexhaustible.’ Better yet, the initial barrel, the cleaned‑out barrel and the drilled‑out shavings all had the same specific heat so no heat had been extracted from anything. He concluded that heat is an aspect of motion, totally contradicting the leading caloric theories and what was left of phlogiston.”

<chuckle> “He was a revolutionary, after all. But what about ‘Enthalpy‘?”

“Here’s an example. Suppose you’ve got a puddle of gasoline, but its temperature is zero kelvins and somehow it’s compressed to zero volume. Add energy to those waggling molecules until the puddle’s at room temperature. Next, push enough atmosphere out of the way to let the puddle expand to its normal size. Pushing the atmosphere takes energy, too — the physicists call that ‘PV work‘ because it’s calculated as the pressure times the volume. The puddle’s enthalpy is its total energy content — thermal plus PV plus the chemical energy you get when it burns.”

~~ Rich Olcott

The Spaghettification Zone

On By rolcottIn Physics: Newton and Gravity, UncategorizedLeave a comment

Vinnie’s still wincing. “That neutron star pulling all the guy’s joints apart — yuckhh! So that’s spaghettification? I thought that was a black hole thing.”

“Yes and no, in that order. Spaghettification’s a tidal phenomenon associated with lopsided gravity fields, black holes or otherwise. You know what causes the tides, of course.”

“Sure, Sy. The Sun pulls up on the water underneath it.”

“That’s not quite it. The Sun’s direct‑line pull on a water molecule is less than a part per million of the Earth’s. What really happens is that the Sun broadly attracts water molecules north‑south east‑west all across the Sun‑side hemisphere. There’s a general movement towards the center of attraction where molecules pile up. The pile‑up’s what we call the tide.”

“What explains the high tide on the other side of the Earth? You can’t claim the Sun pushes it over there.”

“Of course not. It goes back to our lopsided taste of the Sun’s gravitational field. If it weren’t for the Sun’s pull, sea level would be a nice round circle where centrifugal force balances Earth’s gravity. The Sun’s gravity puts its thumb on the scale for the near side, like I said. It’s weaker on the other side, though — balance over there tilts toward the centrifugal force, makes for a far‑side bulge and midnight tides. We get lopsided forces from the moon’s gravity, too. That generates lunar tides. The solar and lunar cycles combine to produce the pattern of tides we experience. But tides can get much stronger. Ever hear of the Roche effect?”

“Can’t say as I have.”

“Imagine the Earth getting closer to the Sun but ignore the heat. What happens?”

Cygnus X-1 Illustration
Credit: NASA, CXC, Melissa Weiss (CXC)

“Sun‑side tides get higher and higher until … the Sun pulls the water away altogether!”

“That’s the idea. In the mid‑1800s Édouard Roche noticed the infinity buried in Newton’s F=GMm/r² equation. He realized that the forces get immense when the center‑to‑center distance, r, gets tiny. ‘Something’s got to give!’ he thought so he worked out the limits. The center‑to‑center force isn’t the critical one. The culprit is the tidal force which arises from the difference in the gravitational strength on either side of an object. When the force difference exceeds the forces holding the object together, it breaks up.”

“Only thing holding the ocean to Earth is gravity.”

“Exactly. Roche’s math applies strictly to objects where gravity’s the major force in play. Things like rubble‑pile asteroids like Bennu and Dimorphos or a black hole sipping the atmosphere off a neighboring blue supergiant star. We relate spaghettification to rubble piles but it can also compete with interatomic electronic forces which are a lot stronger.”

“You’re gonna get quantitative, right?”

“Of course, that’s how I operate.” <tapping on Old Reliable’s screen> “Okay, suppose Niven’s guy Shaffer is approaching some object from far away. I’ve set up tidal force calculations for some interesting cases. Turns out if you know or can estimate an object’s mass and size, you can calculate its density which is key to Roche’s distance where a rubble pile flies apart. You don’t need density for the other thresholds. Spagettification sets in when tidal force is enough to bend a molecule. That’s about 500 newtons per meter, give or take a factor of ten. I estimated the rip‑apart tidal force to be near the tensile strength of the ligaments that hold your bones together. Sound fair?”

“Fair but yucky.”

“Mm‑hm. So here’s the results.”

“What’s with the red numbers?”

“I knew you’d ask that first. Those locations are inside the central object so they make no sense physically. Funny how Niven picked the only object class where stretch and tear effects actually show up.”

“How come there’s blanks under whatever ‘Sgr A*’ is?”

“Astronomer‑ese for ‘Sagittarius A-star,’ the Milky Way’s super‑massive black hole. Can’t properly calculate its density because the volume’s ill‑defined even though we know the Event Horizon’s diameter. Anyhow, look at the huge difference between the Roche radii and the two thresholds that affect chemical bonds.”

“Hey, Niven’s story had Shaffer going down to like 13 miles, about 20 kilometers. He’d’ve been torn apart before he got there.”

“Roughly.”

~~ Rich Olcott

One Step After Another

On By rolcottIn Astronomy: Techniques, UncategorizedLeave a comment

Mid-afternoon, time for a coffee break. As I enter Cal’s shop, I see Cathleen and Kareem chuckling together behind a jumble of Cal’s distinctive graph‑lined paper napkins. “What’s the topic of conversation, guys?”

“Hi, Sy. Kareem and I are comparing ladders.”

I look around, don’t see anything that looks like construction equipment.

“Not that kind, Sy. What’s your definition of a ladder?”

“Getting down to definitions, eh, Kareem? Okay, it’s a framework with steps you can climb up towards something you can’t reach.”

“Well, there you go.”

“Not much help, Cathleen. What are you really bantering about?”

“Each of our fields of study has a framework with steps that let us measure something that’d be way out of reach without it.”

“You’ll appreciate this, Sy — our ladders even use different math. The steps on Cathleen’s ladder are mostly linear, mine are mostly exponential.”

“And they’re both finicky — you have to be really careful when using them.”

“And they’ve both recently had adjustments at the top end.”

“I can see the fun, I think. How about some specifics?”

They exchange a look, Kareem gestures ‘after you‘ and Cathleen opens. “Mine’s in astrometry, Sy, the precise recording of relative positions. Tycho Brahe’s numbers were good to a few dozen arcseconds—”

“Arcsecond?”

“1/60 of an arcminute which is 1/60 of a degree which is 1/360 of a full circle around the sky. Good enough in Newton’s day for him to explain planetary orbits, but we’ve come <ahem> a long way since then. The Gaia telescope mission can resolve certain objects down to a few microarcseconds but that’s only half the problem.”

“Let me guess — you have angles but you don’t have distances.”

“Bingo. Distance is astrometry’s biggest challenge.”

“Wait, Newton’s Law of Gravity includes r as the distance between objects. For that matter, Kepler’s Laws use r² and r³. Couldn’t you juggle them around to evaluate r?”

“Nope. Kepler did ratios, not absolute values. Newton’s Law has r² but you can rewrite it as F ² = GMm/r² = G(M/r)(m/r), G times the product of two mass‑to‑distance ratios. Newton’s G is our least‑accurate physical constant and we don’t have good handles on either of those numerators. Before space flight we just had mass ratios like M/m. We only discovered the Moon’s absolute mass when we orbited it with spacecraft of known mass. That’s the lowest rung on our mass ladder. Inside the Solar System we go step by step with orbit ratios. Outside the system everything’s measured relative to Solar mass.”

“I’m getting the ladder idea. So how do you distances?”

“Lowest rung is parallax, like binocular vision. You look at something from two different points a known distance apart. Measure the angle between the sight‑lines. Figure the triangles to get the something’s distance. The earliest example I know of was in the mid‑1700s when astrometers thousands of miles apart on Earth watched Venus cross the Sun’s disk. Each recorded the precise time they saw Venus touch the Sun’s disk. Given the time shift and the on‑Earth distance, some trigonometry gave them the Earth‑Venus distance. That put a scale to Newtonian orbital diagrams. Parallax across the width of Earth’s orbit yielded stellar distances out to thousands of lightyears with Hubble. We expect ten times better from Gaia.”

“That gets you maybe across the Milky Way. What about farther out?”

“Several ingenious variations on the parallax idea, but mostly standard candles.”

“Candles?”

“Suppose you measure the brightness of a candle that’s a known distance away and there’s an equally luminous candle some unknown distance away. Measured brightness falls as the square of the distance, so if the second candle appears half as bright it’s four times the distance and so on. Climbing the cosmic distance ladder is going from one kind of uniformly‑luminous candle to another kind farther away.”

“Such as?”

“We know how brightness relates to bright‑dim‑bright cycle time for several types of variable stars. That gets us out to 30 million lightyears or so. Type I‑a supernovas act as useful candles out to a billion lightyears. Beyond that we can use galaxy surface brightness. That’s where the recent argument started.”

~ Rich Olcott

  • Thanks to Ken Burke for mentioning tellurium‑128’s septillion‑year half‑life.

Mushy stuff

On By rolcottIn Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

“Amanda! Amanda! Amanda!”

“All right, everyone, settle down for our final Crazy Theorist. Jim, you’re up.”

“Thanks, Cathleen. To be honest I’m a little uncomfortable because what I’ve prepared looks like a follow-on to Newt’s idea but we didn’t plan it that way. This is about something I’ve been puzzling over. Like Newt said, black holes have mass, which is what everyone pays attention to, and charge, which is mostly unimportant, and spin. Spin’s what I’ve been pondering. We’ve all got this picture of a perfect black sphere, so how do we know it’s spinning?”

Voice from the back of the room — “Maybe it’s got lumps or something on it.”

“Nope. The No-hair Theorem says the event horizon is mathematically smooth, no distinguishing marks or tattoos. Question, Jeremy?”

“Yessir. Suppose an asteroid or something falls in. Time dilation makes it look like it’s going slower and slower as it gets close to the event horizon, right? Wouldn’t the stuck asteroid be a marker to track the black hole’s rotation?”

“Excellent question.” <Several of Jeremy’s groupies go, “Oooh.”> “Two things to pay attention to here. First, if we can see the asteroid, it’s not yet inside the horizon so it wouldn’t be a direct marker. Beyond that, the hole’s rotation drags nearby spacetime around with it in the ergosphere, that pumpkin‑shaped region surrounding the event horizon except at the rotational poles. As soon as the asteroid penetrates the ergosphere it gets dragged along. From our perspective the asteroid spirals in instead of dropping straight. What with time dilation, if the hole’s spinning fast enough we could even see multiple images of the same asteroid at different levels approaching the horizon.”

Jeremy and all his groupies go, “Oooh.”

“Anyhow, astronomical observation has given us lots of evidence that black holes do spin. I’ve been pondering what’s spinning in there. Most people seem to think that once an object crosses the event horizon it becomes quantum mush. There’d be this great mass of mush spinning like a ball. In fact, that was Schwarzchild’s model for his non-rotating black hole — a simple sphere of incompressible fluid that has the same density throughout, even at the central singularity.”

VBOR — “Boring!”

“Well yeah, but it might be correct, especially if spaghettification and the Firewall act to grind everything down to subatomic particles on the way in. But I got a different idea when I started thinking about what happened to those two black holes that LIGO heard collide in 2015. It just didn’t seem reasonable that both of those objects, each dozens of solar masses in size, would get mushed in the few seconds it took to collide. Question, Vinnie?”

“Yeah, nice talk so far. Hey, Sy and me, we talked a while ago about you can’t have a black hole inside another black hole, right, Sy?”

“That’s not quite what I said, Vinnie. What I proved was that after two black holes collide they can’t both still be black holes inside the big one. That’s different and I don’t think that’s where Jim’s going with this.”

“Right, Mr Moire. I’m not claiming that our two colliders retain their black hole identities. My crazy theory is that each one persists as a high‑density nubbin in an ocean of mush and the nubbins continue to orbit in there as gravity propels them towards the singularity.”

VBOR —”Orbit? Like they just keep that dance going after the collision?”

“Sure. What we can see of their collision is an interaction between the two event horizons and all the external structures. From the outside, we’d see a large part of each object’s mass eternally inbound, locked into the time dilation just above the joined horizon. From the infalling mass perspective, though, the nubbins are still far apart. They collide farther in and farther into the future. The event horizon collision is in their past, and each nubbin still has a lot of angular momentum to stir into the mush. Spin is stirred-up mush.”

Cathleen’s back at the mic. “Well, there you have it. Amanda’s male-pattern baldness theory, Newt’s hyper‑planetary gear, Kareem’s purple snowball or Jim’s mush. Who wins the Ceremonial Broom?”

The claque responds — “Amanda! Amanda! Amanda!”

~ Rich Olcott

A Virial Homework Problem

On By rolcottIn Astronomy: Techniques, Physics: Entropy and Thermodynamics, Uncategorized1 Comment

“Uh, Mr Moire? Would you mind if we used Old Reliable to do the calculations on this problem about the galaxy cluster’s Virial?”

Data extracted and re-scaled from Fig 2 of Smith (1936), The Mass of the Virgo Cluster

“Mm, only if you direct the computation, Jeremy. I want to be able to face Professor Hanneken with a clear conscience if your name ever comes up in the conversation. Where do we start?”

“With the data he printed here on the other side of the problem sheet. Old Reliable can scan it in, right?”

“Certainly. What are the columns?”

“The first one’s clear. The second column is the distance between the galaxy and the center of the cluster. Professor Hanneken said the published data was in degrees but he converted that to kiloparsecs to get past a complication of some sort. The third column is, umm, ‘the relative line‑of‑sight velocity.’ I understand the line‑of‑sight part, but the numbers don’t look relativistic.”

“You’re right, they’re much smaller than lightspeed’s 300,000 km/s. I’m sure the author was referring to each galaxy’s motion relative to the other ones. That’s what the Virial’s about, after all. I’ll bet John also subtracted the cluster’s average velocity from each of the measured values because we don’t care about how the galaxies move relative to us. Okay, we’ve scanned your data. What do we do next?”

“Chart it, please, in a scatter plot. That’s always the first thing I do.”

“Wise choice. Here you go. What do we learn from this?”

“On the whole it looks pretty flat. Both fast and slow speeds are spread across the whole cluster. If the whole cluster’s rotating we’d see faster galaxies near the center but we don’t. They’re all moving randomly so the Virial idea should apply, right?”

“Mm-hm. Does it bother you that we’re only looking at motion towards or away from us?”

“Uhh, I hadn’t thought about that. You’re right, galaxy movements across the sky would be way too slow for us to detect. I guess the slowest ones here could actually be moving as fast as the others but they’re going crosswise. How do we correct for that?”

“Won’t need much adjustment. The measured numbers probably skew low but the average should be correct within a factor of 2. What’s next?”

“Let’s do the kinetic energy piece T. That’d be the average of galaxy mass m times v²/2 for each galaxy. But we don’t know the masses. For that matter, the potential energy piece, V=G·M·m/R, also needs galaxy mass.”

“If you divide each piece by m you get specific energy, joules/kilogram of galaxy. That’s the same as (km/s)². Does that help?”

“Cool. So have Old Reliable calculate v²/2 for each galaxy, then take the average.”

“We get 208,448 J/kg, which is too many significant figures but never mind. Now what?”

“Twice T would be 416,896 which the Virial Theorem says equals the specific potential energy. That’d be Newton’s G times the cluster mass M divided by the average distance R. Wait, we don’t know M but we do know everything else so we can find M. And dividing that by the galaxy count would be average mass per galaxy. So take the average of all the R distances, times the 416,896 number, and divide that by G.”

“What units do you want G in?”

“Mmm… To cancel the units right we need J/kg times parsecs over … can we do solar masses? That’d be easier to think about than kilograms.”

“Old Reliable says G = 4.3×10-3 (J/kg)·pc/Mʘ. Also, the average R is … 890,751 parsecs. Calculating M=v²·R/G … says M is about 90 trillion solar masses. With 29 galaxies the average is around 3 trillion solar masses give or take a couple of factors of 2 or so.”

“But that’s a crazy number, Mr Moire. The Milky Way only has 100 billion stars.”

“Sometimes when the numbers are crazy, we’ve done something wrong. Sometimes the numbers tell us something. These numbers mutter ‘dark matter‘ but in the 1930s only Fritz Zwicky was listening.”

~~ Rich Olcott

  • Thanks again to Dr KaChun Yu for pointing out Sinclair Smith’s 1936 paper. Naturally, any errors in this post are my own.

Why Physics Is Complex

On By rolcottIn Mathematics, Physics: Light and Relativity, Physics: Quantum Mechanics, UncategorizedLeave a comment

“I guess I’m not surprised, Sy.”

“At what, Vinnie?”

“That quantum uses these imaginary numbers — sorry, you’d prefer we call them i‑numbers.”

“Makes no difference to me, Vinnie. Descartes’ pejorative term has been around for three centuries so that’s what the literature uses. It’s just that most people pick up the basic idea more quickly without the woo baggage that the real/imaginary nomenclature carries along. So, yes, it’s true that both i‑numbers and quantum mechanics appear mystical, but really quantum mechanics is the weird one. And relativity.”

“Wait, relativity too? That’s hard to imagine, HAW!”

“Were you in the room for Jim’s Open Mic session where he talked about Minkowski’s geometry?”

“Nope, missed that.”

“Ah, okay. Do you remember the formula for the diagonal of a rectangle?”

“That’d be the hypotenuse formula, c²=a²+b². Told you I was good at Geometry.”

“Let’s use ‘d‘ for distance, because we’re going to need ‘c‘ for the speed of light. While we’re at it, let’s replace your ‘a and ‘b‘ with ‘x‘ and ‘y,’ okay?”

“Sure, why not?”

<casting image onto office monitor> “So the formula for the body diagonal of this box is…”

“Umm … That blue line across the bottom’s still √(x²+y²) and it’s part of another right triangle. d‘s gotta be the square root of x²+y²+z².”

“Great. Now for a fourth dimension, time, so call it ‘t.’ Say we’re going for light’s path between A at one moment and B some time t later.”

“Easy. Square root of x²+y²+z²+t².”

“That’s almost a good answer.”

“Almost?”

“The x, y and z are distance but t is a duration. The units are different so you can’t just add the numbers together. It’d be like adding apples to bicycles.”

“Distance is time times speed, so we multiply time by lightspeed to make distance traveled. The formula’s x²+y²+z²+(ct)². Better?”

“In Euclid’s or Newton’s world that’d be just fine. Not so much in our Universe where Einstein’s General Relativity sets the rules. Einstein or Minkowski, no‑one knows which one, realized that time is fundamentally perpendicular to space so it works by i‑numbers. You need to multiply t by ic.”

“But i²=–1 so that makes the formula x²+y²+z²–(ct)².”

“Which is Minkowski’s ‘interval‘ between an event at A and another event at B. Can’t do relativity work without using intervals and complex numbers.”

“Well that’s nice but we started talking about quantum. Where do your i‑numbers come into play there?”

“It goes back to the wave equation— no, I know you hate equations. Visualize an ocean wave and think about describing its surface curvature.”

Adapted from “The Great Wave off Kanagawa”
by Katsushika Hokusai, in public domain

“Curvature?”

“How abruptly the slope changes. If the surface is flat the slope is zero everywhere and the curvature is zero. Up near the peak the slope changes drastically within a short distance and we say the surface is highly curved. With me?”

“So far.”

“Good. Now, visualize the wave moving past you at some convenient speed. Does it make sense that the slope change per unit time is proportional to the curvature?”

“The pointier the wave segment, the faster its slope has to change. Yeah, makes sense.”

“Which is what the classical wave equation says — ‘time‑change is proportional to space‑change’. The quantum wave equation is fundamental to QM and has exactly the same form, except there’s an i in the proportionality constant and that changes how the waves work.” <casting a video> “The equation’s general solution has a complex exponential factor eix. At any point its value is a single complex number with two components. From the x‑direction, the circle looks like a sine wave. From the i‑direction it also looks like a sine wave, but out of phase with the x‑wave, okay?”

A traveling wave packet.
Image by “Xcodexif” under CCS-A 4.0 license

“Out of phase?”

“When one wave peaks, the other’s at zero and vice‑versa. The point is, rotation’s built into the quantum waves because of that i‑component.” <another video> “Here’s a lovely example — that black dot emits a photon that twists and releases the electromagnetic field as it moves along.”

~ Rich Olcott