Category: Physics: Entropy and Thermodynamics

Deep Dive

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Sy, I’m trying to get my head wrapped around how the potential‑kinetic energy thing connects with your enthalpy thing.”

“Alright, Vinnie, what’s your cut so far?”

“It has to do with scale. Big things, like us and planets, we can see things moving and so we know they got kinetic energy. If they’re not moving steady in a straight line we know they’re swapping kinetic energy, give and take, with some kind of potential energy, probably gravity or electromagnetic. Gravity pulls things into a circle unless angular momentum gets in the way. How’m I doing so far?”

“I’d tweak that a little, but nothing to argue with. Keep at it.”

“Yeah, I know the moving is relative to whether we’re in the same reference frame and all that. Beside the point, gimme a break. So anyway, down to the quantum level. Here you say heat makes the molecules waggle so that’s kinetic energy. What’s potential energy like down there?”

<grabs another paper napkin> “Here’s a quick sketch of the major patterns.”

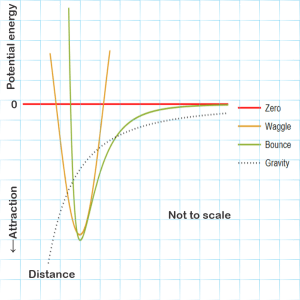
“Hmm. You give up potential energy when you fall and gravity’s graph goes down from zero to more negative forever, I guess, so gravity’s always attracting.”

“Pretty much, but at this level we don’t have to bother with gravity at all. It’s about a factor of 1038 weaker than electric interactions. Molecular motions are dominated by electromagnetic fields. Some are from a molecule’s other internal components, some from whatever’s around that brandishes a charge. We’ve got two basic patterns. One of them, I’m labeling it ‘Waggle,’ works like a pendulum, sweeping up and down that U‑shape around some minimum position, high kinetic energy where the potential energy’s lowest and vice‑versa. You know how water’s H‑O‑H molecules have that the V‑shape?”

“Yeah, me you and Eddie talked about that once.”

“Mm‑hm. Well, the V‑shape gives that molecule three different ways to waggle. One’s like breathing, both sides out then both sides in. If the hydrogens move too far from the oxygen, that stretches their chemical bonds and increases their potential energy so they turn around and go back. If they get too close, same thing. Bond strength is about the depth of the U. The poor hydrogens just stretch in and out eternally, swinging up and down that symmetric curve.”

“Awww.”

“That’s a chemist’s picture. The physics picture is cloudier. In the quantum version, over here’s a trio of fuzzy quarks whirling around each other to make a proton. Over there’s a slightly different fuzzy trio pirouetting as a neutron. Sixteen of those roiling about make up the oxygen nucleus plus two more for the hydrogens plus all their electrons — imagine a swarm of gnats. On the average the oxygen cloud and the two hydrogen clouds configure near the minimum of that U‑shaped potential curve but there’s a lot of drifting that looks like symmetrical breathing.”

“What about the other two waggles?”

“I knew you’d ask. One’s like the two sides of a teeterboard, oscillating in and out asymmetrically. The other’s a twist, one side coming toward you and then the other side. Each waggle has its own distinct set of resistance forces that define its own version of waggle curve. Each kind interacts with different wavelengths of infrared light which is how we even know about them. Waggle’s official name is ‘harmonic oscillator.’ More complicated molecules have lots of them.”

“What’s that ‘bounce’ curve about?”

“Officially that’s a Lennard-Jones potential, the simplest version of a whole family of curves for modeling how molecules bounce off each other. Little or no interaction at large distances, serious repulson if two clouds get too close, and a little stickiness at some sweet-spot distance. If it weren’t for the stickiness, the Ideal Gas Law would work even better than it does. So has your head wrapped better?”

“Sorta. From what I’ve seen, enthalpy’s PV part doesn’t apply in quantum. The heat capacity part comes from your waggles which is kinetic energy even if it’s clouds moving. Coming the other way, quantum potential energy becomes enthalpy’s chemical part with breaking and making chemical bonds. Did I bridge the gap?”

“Mostly, if you insist on avoiding equations.”

~ Rich Olcott

Up, Down And Between

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized1 Comment

Vinnie finishes his double‑pepperoni pizza. “Sy, these enthalpies got a pressure‑volume part and a temperature‑heat capacity part, but seems to me the most important part is the chemical energy.”

I’m still working on my slice (cheese and sausage). “That’s certainly true from a fuel engineering perspective, Vinnie. Here’s a clue. Check the values in this table for 0°C, also known as 273K.”

Link to Larger image

“Waitaminute! That line says the enthalpy’s exactly zero under the book‘s conditions. We talked about zeros a long time ago. All measurements have error. Nothing’s exactly zero unless it’s defined that way or it’s Absolute Zero temperature and we’ll never get there. Is this another definition thing?”

“More of a convenience thing. The altimeters in those planes you fly, do they display the distance to Earth’s center?”

“Nope, altitude above sea level, if they’re calibrated right.”

“But the other would work, too, say as a percentage of the average radius?”

“Not really. Earth’s fatter at the Equator than it is at the poles. You’d always have to correct for latitude. And the numbers would be clumsy, always some fraction of a percent of whatever the average is—”

“6371 kilometers.”

“Yeah, that. Try working with fractions of a part per thousand when you’re coming in through a thunderstorm. Give me kilometers or feet above sea level and I’m a lot happier.”

“But say you’re landing in Denver, 1.6 kilometers above sea level.”

“It’s a lot easier to subtract 1.6 from baseline altitude in kilometers than 0.00025 from 1.00something and getting the decimals right. Sea‑level calibrations are a lot easier to work with.”

“So now you know why the book shows zero enthalpy for water at 273K.”

“You’re saying there’s not really zero chemical energy in there, it’s just a convenient place to start counting?”

“That’s exactly what I’m saying. Chemical energy is just another form of potential energy. Zeroes on a potential scale are arbitrary. What’s important is the difference between initial and final states. Altitude’s about gravitational potential relative to the ground; chemists care about chemical potential relative to a specific reaction’s final products. Both concerns are about where you started and where you stop.”

“Gimme a chemical f’rinstance.”

<reading off of Old Reliable> “Reacting 1 gram of oxygen gas and 0.14 gram of hydrogen gas slowly in a catalytic fuel cell at 298K and atmospheric pressure produces one gram of liquid water and releases 18.1 kilojoules of energy. Exploding the same gas mix at the same pressure in a piston also yields 18.1 kilojoules once you cool everything back down to 298K. Different routes, same results.”

Meanwhile, Jeremy’s wandered over from his gelato stand. “Excuse me, Mr Moire. I read your Crazy Theory about how mammals like to keep their body temperature in the range near water’s minimum Specific Heat, um Heat Capacity, but now I’m confused.”

“What’s the confusion, Jeremy?”

“Well, what you told me before made sense, about increased temperature activates higher‑energy kinds of molecular waggling to absorb the heat. But that means that Heat Capacity always ought to increase with increasing temperature, right?”

“Good thinking. So your problem is…?

“Your graph shows that if water’s cold, warming it decreases its Heat Capacity. Do hotter water molecules waggle less?”

“No, it’s a context thing. Gas and liquid are different contexts. Each molecule in a gas is all by itself, most of the time, so its waggling is determined only by its internal bonding and mass configuration. Put that molecule into a liquid or solid, it’s subject to what its neighbors are doing. Water’s particularly good at intermolecular interactions. You know about the hexagonal structure locked into ice and snowflakes. When water ice melts but it’s still at low temperature, much of the hexagonal structure hangs around in a mushy state. A loose structure’s whole‑body quivering can absorb heat energy without exciting waggles in its constituent molecules. Raising the temperature disrupts that floppy structure. That’s most of the fall on the Heat Capacity curve.”

“Ah, then the Sensitivity decrease on the high‑temperature side has to do with blurry structure bits breaking down to tinier pieces that warm up more from less energy. Thanks, Mr Moire.”

“Don’t mention it.”

~~ Rich Olcott

Early Days in The Sunshine

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, Uncategorized1 Comment

“Wait, Sy. From what you just said about rocket fuel, its enthalpic energy content changes if I move it. On the ground it’s ‘chemical energy plus thermal plus Pressure times Volume.’ Up in space, though, the pressure part’s zero. So how come the CRC Handbook people decided it’s worthwhile to publish pages and pages of specific heat and enthalpy tables if it’s all ‘it depends’?”

“We know the dependencies, Vinnie. The numbers cover a wide temperature range but they’re all at atmospheric pressure. ‘Pressure times Volume‘ makes it easy to adjust for pressure change — just do that multiplication and add the result to the other terms. It’s trickier when the pressure varies between here and there but we’ve got math to handle that. The ‘thermal‘ part’s also not a big problem because if you something’s specific heat you know how its energy content changes with temperature change and vice‑versa.”

<checking a chart on his phone> “This says water’s specific heat number changes with temperature. They’re all about 1.0 but some are a little higher and some a little lower. Graph ’em out, looks like there’s a pattern there.”

<tapping on Old Reliable’s screen> “Good eye. High at the extreme temperatures, lower near — that’s interesting.”

Data from CRC handbook, 39th Ed, pp 2081-2082

“What’s that?”

“The range where the curve is flattest, 35 to 40°C. Sound familiar?”

“Yeah, my usual body temperature’s in there, toward the high side if I’ve got a fever. What’s that mean?”

“That’s so far out of my field all I’ve got is guesses. Hold on … there, I’ve added a line for 1/SH.”

“What’s that get you?”

“A different perspective. Specific Heat is the energy change when one gram of something changes temperature by one degree. This new line, I’ve called it Sensitivity, is how many degrees one unit of heat energy will warm the gram. Interesting that both curves flatten out in exactly the temperature range that mammals like us try to maintain. The question is, why do mammals prefer that range?”

“And your answer is?”

“A guess. Remember, I’m not a biologist or a biochemist and I haven’t studied how biomolecules interact with water.”

“I get that we should file this under Crazy Theories. Out with it.”

“Okay. Suppose it’s early days in mammalian evolution. You’re one of those early beasties. You’re not cold-blooded like a reptile, you’re equipped with a thermostat for your warm blood. Maybe you shiver if you’re cold, pant if you’re hot, doesn’t matter. What does matter is, your thermostat has a target temperature. Suppose your target’s on the graph’s coolish left side where water’s sensitivity rises rapidly. You’re sunning yourself on a flat rock, all parts of you getting the same calories per hour.”

“That’s on the sunward side. Shady side not so much.”

“Good point. I’ll get to that. On the sunward side you’re absorbing energy and getting warm, but the warmer you get the more your heat sensitivity rises. Near your target point your tissues warm up say 0.4 degree per unit of sunlight, but after some warming those tissues are heating by 0.6 degrees for the same energy input.”

“I recognize positive feedback when I see it, Sy. Every minute on that rock drives me further away from my target temperature. Whoa! But on the shady side I don’t have that problem.”

“That’s even messier. You’ve got a temperature disparity between the two sides and it’s increasing. Can your primitive circulatory system handle that? Suppose you’re smart enough to scurry out of the sunlight. You’ve still got a problem. There’s more to you than your skin. You’ve got muscles and those muscles have cells and those cells do biochemistry. Every chemical reaction inside you gives off at least a little heat for more positive feedback.”

“What if my thermostat’s set over there on the hot side?”

“You’d be happy in the daytime but you’d have a problem at night. For every degree you chill below comfortable, you need to generate a greater amount of energy to get back up to your target setting.”

“Smart of evolution to set my thermostat where water’s specific heat changes least with temperature.”

“That’s my guess.”

~~ Rich Olcott

Hiding Under Many Guises

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized3 Comments

Vinnie lifts his pizza slice and pauses. “I dunno, Sy, this Pressure‑Volume part of enthalpy, how is it energy so you can just add or subtract it from the thermal and chemical kinds?”

“Fair question, Vinnie. It stumped scientists through the end of Napoleon’s day until Sadi Carnot bridged the gap by inventing thermodynamics.”

“Sounds like a big deal from the way you said that.”

“Oh, it was. But first let’s clear the ‘is it energy?’ question. How would Newton have calculated the work you did lifting that slice?”

“How much force I used times the distance it moved.”

“Putting units to that, it’d be force in newtons times distance in meters. A newton is one kilogram accelerated by one meter per second each second so your force‑distance work there is measured in kilograms times meters‑squared divided by seconds‑squared. With me?”

“Hold on — ‘per second each second’ turned into ‘per second‑squared.” <pause> “Okay, go on.”

“What’s Einstein’s famous equation?”

“Easy, E=mc².”

“Mm-hm. Putting units to that, c is in meters per second, so energy is kilograms times meters‑squared divided by seconds‑squared. Sound familiar?”

“Any time I’ve got that combination I’ve got energy?”

“Mostly. Here’s another example — a piston under pressure. Pressure is force per unit area. The piston’s area is in square meters so the force it feels is newtons per meter‑squared, times square meters, or just newtons. The piston travels some distance so you’ve got newtons times meters.”

“That’s force‑distance work units so it’s energy, too.”

“Right. Now break it down another way. When the piston travels that distance, the piston’s area sweeps through a volume measured in meters‑cubed, right?”

“You’re gonna say pressure times volume gives me the same units as energy?”

“Work it out. Here’s a paper napkin.”

“Dang, I hate equations … Hey, sure enough, it boils down to kilograms times meters‑squared divided by seconds‑squared again!”

“There you go. One more. The Ideal Gas Law is real simple equation —”

“Gaah, equations!”

“Bear with me, it’s just PV=nRT.”

“Is that the same PV so it’s energy again?”

“Sure is. The n measures the amount of some gas, could be in grams or whatever. The R, called the Gas Constant, is there to make the units come out right. T‘s the absolute temperature. Point is, this equation gives us the basis for enthalpy’s chemical+PV+thermal arithmetic.”

“And that’s where this Carnot guy comes in.”

“Carnot and a host of other physicists. Boyle, Gay‑Lussac, Avagadro and others contributed to Clapeyron’s gas law. Carnot’s 1824 book tied the gas narrative to the energetics narrative that Descartes, Leibniz, Newton and such had been working on. Carnot did it with an Einstein‑style thought experiment — an imaginary perfect engine.”

“Anything perfect is imaginary, I know that much. How’s it supposed to work?”

<sketching on another paper napkin> “Here’s the general idea. There’s a sealed cylinder in the middle containing a piston that can move vertically. Above the piston there’s what Carnot called ‘a working body,’ which could be anything that expands and contracts with temperature.”

“Steam, huh?”

“Could be, or alcohol vapor or a big lump of iron, whatever. Carnot’s argument was so general that the composition doesn’t matter. Below the piston there’s a mechanism to transfer power from or to the piston. Then we’ve got a heat source and a heat sink, each of which can be connected to the cylinder or not.”

“Looks straight‑forward.”

“These days, sure. Not in 1824. Carnot’s gadget operates in four phases. In generator mode the working body starts in a contracted state connected to the hot Th source. The body expands, yielding PV energy. In phase 2, the body continues to expand while it while it stays at Th. Phase 3, switch to the cold Tc heat sink. That cools the body so it contracts and absorbs PV energy. Phase 4 compresses the body to heat it back to Th, completing the cycle.”

“How did he keep the phases separate?”

“Only conceptually. In real life Phases 1 and 2 would occur simultaneously. Carnot’s crucial contribution was to treat them separately and yet demonstrate how they’re related. Unfortunately, he died of scarlet fever before Clapeyron and Clausius publicized and completed his work.”

~ Rich Olcott

Energy Is A Shape-shifter

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Another dinner, another pizza at Eddie’s place. Vinnie wanders over to my table. “Hi, Sy, got a minute?”

“Not doing anything other than eating, Vinnie. What’s on your mind other than the sound of my chewing?”

“At least you keep your mouth closed. No, it’s about this energy thing you’ve gotten back into. I read that enthalpy piece and it’s bothering me.”

“In what way?”

“Well, you said that something’s enthalpy is the energy total of ‘thermal plus Pressure‑Volume plus chemical energy,’ right? I’m trying to fit that together with the potential energy and kinetic energy we talked about a while ago. It’s not working.”

“Deep question for dinner time but worth the effort. Would it help if I told you that the ‘actual versus potential’ notion goes back to Aristotle, the ‘kinetic’ idea came from Newton’s enemy Leibniz, but ‘enthalpy’ wasn’t a word until the 20th century?”

“Not a bit.”

“Didn’t think it would. Here’s another way to look at it. The thinkers prior to the mid‑1700s all looked at lumpy matter — pendulums, rolling balls on a ramp, planets, missiles — either alone or floating in space or colliding with each other. You could in principle calculate kinetic and potential energy for each lump, but that wasn’t enough when the Industrial Revolution came along.”

“What more did they want?”

“Fuel was suddenly for more than cooking and heating the house. Before then, all you needed to know was whether the log pile was stocked better than it was last year. If not, you might have a few chilly early Spring days but you could get past that. Then the Revolution came along. Miners loved Watt’s coal‑fired water‑pump except if you bought one and ran out of coal then the mine flooded. The miners learned that some kinds of coal burned hotter than others. You didn’t need as much of the good kind for a day’s pumping. The demand for a coal‑rating system got the scientists interested, but those lumps of coal weren’t falling or colliding, they just sat there with their heat locked inside. The classical energy quantities didn’t seem to apply so it was time to invent a new kind of energy.”

“That’s how Conservation of Energy works? You just spread the definition out a little?”

“That’s the current status of dark energy, for instance. We know the galaxies are moving apart against gravity so dark energy’s in there to balance the books. We have no good idea why it exists or where it comes from, but we can calculate it. ‘Internal energy’ put the Victorian‑era physicists in the same pickle — ‘atom’ and ‘molecule’ were notions from Greek and Roman times but none of the Victorians seriously believed in them. The notion of chemical bond energy didn’t crop up until the twentieth century. Lacking a good theory, all the Victorians could do was measure and tabulate heat output from different chemical reactions, the data that went into handbooks like the CRC. Naturally they had to invent thermodynamics for doing the energy accountancy.”

“But if it’s just book-balancing, how do you know the energy is real?”

“Because all the different forms of energy convert to each other. Think of a rocket going up to meet the ISS. Some of the rocket fuel’s chemical energy goes into giving the craft gravitational potential energy just getting it up there. At the same time, most of the chemical energy becomes kinetic energy as the craft reaches the 27600 km/h speed it needs to orbit at that altitude.”

<grin> “All?”

“Okay, we haven’t figured out how to harness dark energy. Yet.”

“HAW! Wait, how does enthalpy’s ‘chemical+PV+thermal’ work when the pressure’s zero, like out in space?”

“Then no work was done against an atmosphere up there to make way for the volume. Suppose you suddenly transported a jug of fuel from Earth up to just outside of the ISS. Same amount of fuel, so same amount of chemical energy, right? Same temperature so same thermal component?”

“I suppose.”

“The volume that the jug had occupied on Earth, what happened to it?”

“Suddenly closed in, probably with a little thud.”

“The thud sound’s where the Earth‑side PV energy went. It all balances out.”

~ Rich Olcott

New (Old) Word: Frigorific!

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

A quiet morning at Cal’s Coffee. I’m sipping my morning mud when Susan Kim bustles to my table, mocha latte in hand. “There you are, Sy. I loved your posts in tribute to the well‑thumbed copy of the CRC Handbook on my desk.”

“Glad you enjoyed them.”

“Your Rumford stuff made it even better because I did a class report on him once so I caught your ‘frigorific‘ reference. What do you know about the background to that?”

“Not much. Didn’t sound like a real word when I ran across it.”

“Oh, it’s a real word but it has a technical meaning now that it didn’t in Newton’s time. Back then it was only about making something cold. These days we also use the word for a mixture that maintains a dependable cold temperature. Liquid water and ice, for instance, stays at 0°C as long as there’s still ice in the cold bath. I used to use an ammonium chloride/water frigorific when I needed something down around -15°C. Now of course I use a benchtop refrigerator.”

“Rumford would have liked that. What were the ‘frigorific rays‘ he got all excited about?”

“Long story but there’s a couple of fun twists. Background first. At the end of the 1700s there was a <grin> heated debate about heat. The phlogiston theory was dead by that time but people still liked the idea that heat was a material fluid. It addressed some chemical puzzles but heat transmission was still mysterious. Everyone knew that a hot object gives off heat by radiation, that the radiation travels in straight lines and that it’s reflected by metal mirrors.”

“Right, the Greeks are supposed to have used huge sun‑focusing mirrors to burn up attacking Roman ships.”

“Maybe. Anyhow, those properties connected heat with light. However, a pane of glass blocks radiated heat, at least until the glass gets hot. People argued this meant heat and light weren’t connected. About 1790 a group of physicists loosely associated with the Academy of Geneva dove into the fray. Rumford was in the group, along with Prévost, Saussure and his student Pictet. They had lots of fun with heat theories and experiments. One of Pictet’s experiments lit Rumford’s fire, so to speak.”

“Good one.”

<smile> “It’s a fairly simple setup that a high school science teacher could do. Pictet hung a concave metallic mirror facing down from the ceiling of a draft‑free room. He placed another concave metallic mirror at floor level immediately beneath it, facing upward. He probably used spherical mirrors which are easy to make, but they could have been elliptical or parabolic sections. Anyhow, he put a thermoscope at the upper mirror’s focal point and a hot object at the lower focal point. Sure enough, the upper focal point got hotter, just as you’d expect.”

“No great surprise, the Greeks would have expected that, too.”

“The surprise happened when he put a cold object in there. The thermoscope’s droplet moved in the cold direction.”

“Wait, like anti‑infrared?”

“That’s the effect. Wave‑theory supporter Rumford took that thought, called it ‘frigorific radiation‘ and ran with it. He constructed a whole thesis around cold waves and heat waves as symmetric partners. He maintained wave intensity, both kinds, increases with temperature difference. Our heat sources are hundreds or thousand of degrees hotter than we are but our cold sources are at most a few dozen degrees colder. By his theory that’s why cold wave phenomena are masked by heat waves.”

“Give me a minute. … Ah, got it. The very meaning of a focal point is that all waves end or start there. A cold object at the sending station emits much less infrared than the warm object did. The thermoscope bulb now gets less than it emits. With less input from below its net energy drops. It chills.”

“Nice, Sy. Now for the other twist. Rumford published his theory in 1805. Herschel had already identified infrared radiation in the Sun’s spectrum in 1800. Two strikes against Herschel, I guess — he was British and he was an astronomer. Continental physicists wouldn’t bother to read his stuff.”

~ Rich Olcott

Rumford’s Boring Story

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Okay, Mr Moire, my grandfather’s engineering handbook has Specific Heat tables because Specific Heat measures molecular wabbling. If he’s got them, though, why’s Enthalpy in the handbook, too?”

“Enthalpy’s not my favorite technical term, Jeremy. It’s wound up in a centuries‑old muddle. Nobody back then had a good, crisp notion of energy. Descartes, Leibniz, Newton and a host of German engineers and aristocratic French hobby physicists all recognized that something made motion happen but everyone had their own take on what that was and how to calculate its effects. They used a slew of terms like vis viva, ‘quantity of motion,’ ‘driving force,’ ‘quantity of work,’ a couple of different definitions of ‘momentum‘ — it was a mess. It didn’t help that a lot of the argument went on before Euler’s algebraic notations were widely adopted; technical arguments without math are cumbersome and can get vague and ambiguous. Lots of lovely theories but none of them worked all that well in the real world.”

“Isn’t that usually what happens? I always have problems in the labs.”

“You’re not alone. Centuries ago, Newton’s Laws of Motion and Gravity made good predictions for planets, not so good for artillery trajectories. Gunners always had to throw in correction factors because their missiles fell short. Massachusetts‑born Benjamin Thompson, himself an artilleryman, found part of the reason.”

“Should I know that name?”

“In later years he became Count Rumford. One of those people who get itchy if they’re not creating something. He was particularly interested in heat — how to trap it and how to make it go where you want.”

“Wait, he was an American but he was a Count? I thought that was illegal.”

“Oh, he left the States before they were the States. During the Revolution he organized a Royalist militia in New York and then lit out for Europe. The Bavarians made him a Count after he spent half‑a‑dozen years doing creative things like reorganizing their army, building public works and introducing potato farming. He concocted a nourishing soup for the poor and invented the soup line for serving it up. But all this time his mind was on a then‑central topic of Physics — what is heat?”

“That was the late 1700s? When everyone said heat was some sort of fluid they called ‘caloric‘?”

“Not everyone, and in fact there were competing theories about caloric — an early version of the particle‑versus‑wave controversy. For a while Rumford even supported the notion that ‘frigorific’ radiation transmitted cold the same way that caloric rays transmitted heat. Whatever, his important contributions were more practical and experimental than theoretical. His redesign of the common fireplace was such an improvement that it took first England and then Europe by storm. Long‑term, though, we remember him for a side observation that he didn’t think important enough to measure properly.”

“Something to do with heat, I’ll bet.”

“Of course. As a wave theory guy, Rumford stood firmly against the ‘caloric is a fluid‘ camp. ‘If heat is material,‘ he reasoned, ‘then a heat‑generating process must eventually run out of caloric.’ He challenged that notion by drilling out a cannon barrel while it was immersed in cold water. A couple of hours of steady grinding brought the water up to boiling. The heating was steady, too, and apparently ‘inexhaustible.’ Better yet, the initial barrel, the cleaned‑out barrel and the drilled‑out shavings all had the same specific heat so no heat had been extracted from anything. He concluded that heat is an aspect of motion, totally contradicting the leading caloric theories and what was left of phlogiston.”

<chuckle> “He was a revolutionary, after all. But what about ‘Enthalpy‘?”

“Here’s an example. Suppose you’ve got a puddle of gasoline, but its temperature is zero kelvins and somehow it’s compressed to zero volume. Add energy to those waggling molecules until the puddle’s at room temperature. Next, push enough atmosphere out of the way to let the puddle expand to its normal size. Pushing the atmosphere takes energy, too — the physicists call that ‘PV work‘ because it’s calculated as the pressure times the volume. The puddle’s enthalpy is its total energy content — thermal plus PV plus the chemical energy you get when it burns.”

~~ Rich Olcott

It’s in The Book

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, Physics: Quantum Mechanics, UncategorizedLeave a comment

A young man’s knock, eager yet a bit hesitant. “Door’s open, Jeremy, c’mon in.”

“Hi, Mr Moire, I’ve got something to show you. It’s from my acheii, my grandfather. He said he didn’t need it any more now he’s retired so he gave it to me. What do you think?”

“Wow, the CRC Handbook of Chemistry And Physics, in the old format, not the 8½×11″ monster. An achievement award, too — my congratulations to your grandfather. Let’s see … over 3000 pages, and that real thin paper you can read through. It’s still got the math tables in front — they moved those to an Appendix by the time I bought my copy. Oooh yeah, lots of data in here, probably represents millions of grad student lab hours. Tech staff, too. And then their bosses spent time checking the work before publishing.”

“Acheii said I’d have to learn a lot before I could use it properly. I see lots of words in there I don’t recognize.” <opens book to a random page> “See, five- and six‑figure values for, what’re Specific Heat and Enthalpy?”

“Your grandfather’s absolutely correct. Much of the data’s extremely specialized. Most techs, including me, have a few personal‑favorite sections they use a lot, never touch the rest of the book. These particular pages, for instance, would be gold for a someone who designs or operates steam‑driven equipment.”

“But what do these numbers mean?”

“Specific Heat is the amount of heat energy you need to put into a certain mass of something in order to raise its temperature by a certain amount. In the early days the Brits, the Scots really, defined the British Thermal Unit as the amount of energy it took to raise the temperature of one pound of liquid water by one degree Fahrenheit. You’d calculate a fuel purchase according to how many BTUs you’d need. Science work these days is metric so these pages tabulate Specific Heat for a substance in joules per gram per °C. Tech in the field moves slow so BTUs are still popular inside the USA and outside the lab.”

“But these tables show different numbers for different temperatures and they’re all for water. Why water? Why isn’t the Specific Heat the same number for every temperature?”

“Water’s important because most power systems use steam or liquid water as the working fluid or coolant. Explaining why heat capacity varies with temperature was one of the triumphs of 19th‑century science. Turns out it’s all about how atomic motion but atoms were a controversial topic at the time. Ostwald, for instance—”

“Who?”

“Wilhelm Ostwald, one of science’s Big Names in the late 1800s. Chemistry back then was mostly about natural product analysis and seeing what reacted with what. Ostwald put his resources into studying chemical processes themselves, things like crystallization and catalysis. He’s regarded as the founder of Physical Chemistry. Even though he invented the mole he steadfastly maintained that atoms and molecules were nothing more than diffraction‑generated illusions. He liked a different theory but that one didn’t work out.”

“Too bad for him.”

“Oh, he won the first Nobel Prize in Chemistry so no problem. Anyway, back to Specific Heat. In terms of its molecules, how do you raise something’s temperature?”

“Um, temperature’s average kinetic energy, so I’d just make the molecules move faster.”

“Well said, except in the quantum world there’s another option. The molecules can’t just waggle any which way. There are rules. Different molecules do different waggles. Some kinds of motion take more energy to excite than others do. Rule 1 is that the high‑energy waggles don’t get to play until the low‑energy ones are engaged. Raising the temperature is a matter of activating more of the high‑energy waggles. Make sense?”

“Like electron shells in an atom, right? Filling the lowest‑energy shells first unless a photon supplies more energy?”

“Exactly, except we’re talking atoms moving within a molecule. Smaller energies, by a factor of 100 or more. My point is, the heat capacity of a substance depends on which waggles activate as the temperature rises. We didn’t understand heat capacity until we applied quantum thinking to the waggles.”

“What about ‘Enthalpy’ then?”

Crystal photo by JJ Harrison

~ Rich Olcott

Virial Yang And Yin

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“But Mr Moire, how does the Virial Equation even work?”

“Sometimes it doesn’t, Jeremy. There’s an ‘if’ buried deep in the derivation. It only works for a system in equilibrium. Sometimes people use the equation as a test for equilibrium.”

“Sorry, what does that mean?”

“Let’s take your problem galaxy cluster as an example. Suppose the galaxies are all alone in the Universe and far apart even by astronomical standards. Gravity’s going to pull them together. Galaxy i and galaxy j are separated by distance Rij. The potential energy in that interaction is Vij = G·mi·mj / Rij. The R‘s are very large numbers in this picture so the V attractions are very small. The Virial is the average of all the V’s so our starting Virial is nearly zero.”

“Nearly but not quite zero, I get that. Wait, if the potential energy starts near zero when things are far apart, and a falling‑in object gives up potential energy, then whatever potential energy it still has must go negative.”

“It does. The total energy doesn’t change when potential energy converts to kinetic energy so yes, we say potential energy decreases even though the negative number’s magnitude gets larger. It’d be less confusing if we measured potential energy going positive from an everything-all-together situation. However, it makes other things in Physics much simpler if we simply write (change in potential energy)+(change in kinetic energy)=0 so that’s the convention.”

“The distances do eventually get smaller, though.”

“Sure, and as the objects move closer they gain momentum and kinetic energy. Gaining momentum is gaining kinetic energy. You’re used to writing kinetic energy as T=m·v²/2, but momentum is p=m·v so it’s just as correct to write T=p²/2m. The two are different ways of expressing the same quantity. When a system is in equilibrium, individual objects may be gaining or losing potential energy, but the total potential energy across the system has reached its minimum. For a system held together by gravity or electrostatic forces, that’s when the Virial is twice the average kinetic energy. As an equation, V+2T=0.”

“So what you’re saying is, one galaxy might fall so far into the gravity well that its potential energy goes more negative than –2T. But if the cluster’s in equilibrium, galaxy‑galaxy interactions during the fall‑in process speed up other galaxies just enough to make up the difference. On the flip side, if a galaxy’s already in deep, other galaxies will give up a little T to pull it outward to a less negative V.”

“Well stated.”

“But why 2? Why not 3½ or some other number?”

“The 2 comes from the kinetic energy expression’s ½. The multiplier could change depending on how the potential energy varies with distance. For both gravity and electrostatic interactions the potential energy varies the same way and 2 is fine the way it is. In a system with a different rule, say Hooke’s Law for springs and rubber bands, the 2 gets multiplied by something other than unity.”

“All that’s nice and I see how the Virial Equation lets astronomers calculate cluster‑average masses or distances from velocity measurements. I suppose if you also have the masses and distances you can test whether or not a collection of galaxies is in equilibrium. What else can we do with it?”

“People analyze collections of stars the same way, but Professor Hanneken’s a physicist, not an astronomer. He wouldn’t have used class time on the Virial if it weren’t good for a broad list of phenomena in and outside of astronomy. Quantum mechanics, for instance. I’ll give you an important example — the Sun.”

“One star, all by itself? Pretty trivial to take its average.”

“Not averaging the Sun as an object, averaging its plasma contents — hydrogen nuclei and their electrons, buffeted by intense heat all the way down to the nuclear reactions that run near the Sun’s core. It’s gravitational potential energy versus kinetic energy all over again, but at the atomic level this time. The Virial Theorem still holds, even though turbulence and electromagnetic effects generate a complicated situation.”

“I’m glad he didn’t assign that as a homework problem.”

“The semester’s not over yet.”

~~ Rich Olcott

A Virial Homework Problem

On By rolcottIn Astronomy: Techniques, Physics: Entropy and Thermodynamics, Uncategorized1 Comment

“Uh, Mr Moire? Would you mind if we used Old Reliable to do the calculations on this problem about the galaxy cluster’s Virial?”

Data extracted and re-scaled from Fig 2 of Smith (1936), The Mass of the Virgo Cluster

“Mm, only if you direct the computation, Jeremy. I want to be able to face Professor Hanneken with a clear conscience if your name ever comes up in the conversation. Where do we start?”

“With the data he printed here on the other side of the problem sheet. Old Reliable can scan it in, right?”

“Certainly. What are the columns?”

“The first one’s clear. The second column is the distance between the galaxy and the center of the cluster. Professor Hanneken said the published data was in degrees but he converted that to kiloparsecs to get past a complication of some sort. The third column is, umm, ‘the relative line‑of‑sight velocity.’ I understand the line‑of‑sight part, but the numbers don’t look relativistic.”

“You’re right, they’re much smaller than lightspeed’s 300,000 km/s. I’m sure the author was referring to each galaxy’s motion relative to the other ones. That’s what the Virial’s about, after all. I’ll bet John also subtracted the cluster’s average velocity from each of the measured values because we don’t care about how the galaxies move relative to us. Okay, we’ve scanned your data. What do we do next?”

“Chart it, please, in a scatter plot. That’s always the first thing I do.”

“Wise choice. Here you go. What do we learn from this?”

“On the whole it looks pretty flat. Both fast and slow speeds are spread across the whole cluster. If the whole cluster’s rotating we’d see faster galaxies near the center but we don’t. They’re all moving randomly so the Virial idea should apply, right?”

“Mm-hm. Does it bother you that we’re only looking at motion towards or away from us?”

“Uhh, I hadn’t thought about that. You’re right, galaxy movements across the sky would be way too slow for us to detect. I guess the slowest ones here could actually be moving as fast as the others but they’re going crosswise. How do we correct for that?”

“Won’t need much adjustment. The measured numbers probably skew low but the average should be correct within a factor of 2. What’s next?”

“Let’s do the kinetic energy piece T. That’d be the average of galaxy mass m times v²/2 for each galaxy. But we don’t know the masses. For that matter, the potential energy piece, V=G·M·m/R, also needs galaxy mass.”

“If you divide each piece by m you get specific energy, joules/kilogram of galaxy. That’s the same as (km/s)². Does that help?”

“Cool. So have Old Reliable calculate v²/2 for each galaxy, then take the average.”

“We get 208,448 J/kg, which is too many significant figures but never mind. Now what?”

“Twice T would be 416,896 which the Virial Theorem says equals the specific potential energy. That’d be Newton’s G times the cluster mass M divided by the average distance R. Wait, we don’t know M but we do know everything else so we can find M. And dividing that by the galaxy count would be average mass per galaxy. So take the average of all the R distances, times the 416,896 number, and divide that by G.”

“What units do you want G in?”

“Mmm… To cancel the units right we need J/kg times parsecs over … can we do solar masses? That’d be easier to think about than kilograms.”

“Old Reliable says G = 4.3×10-3 (J/kg)·pc/Mʘ. Also, the average R is … 890,751 parsecs. Calculating M=v²·R/G … says M is about 90 trillion solar masses. With 29 galaxies the average is around 3 trillion solar masses give or take a couple of factors of 2 or so.”

“But that’s a crazy number, Mr Moire. The Milky Way only has 100 billion stars.”

“Sometimes when the numbers are crazy, we’ve done something wrong. Sometimes the numbers tell us something. These numbers mutter ‘dark matter‘ but in the 1930s only Fritz Zwicky was listening.”

~~ Rich Olcott

  • Thanks again to Dr KaChun Yu for pointing out Sinclair Smith’s 1936 paper. Naturally, any errors in this post are my own.