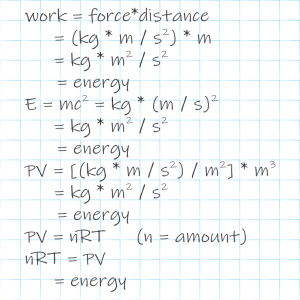Early Days in The Sunshine

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, Uncategorized1 Comment

“Wait, Sy. From what you just said about rocket fuel, its enthalpic energy content changes if I move it. On the ground it’s ‘chemical energy plus thermal plus Pressure times Volume.’ Up in space, though, the pressure part’s zero. So how come the CRC Handbook people decided it’s worthwhile to publish pages and pages of specific heat and enthalpy tables if it’s all ‘it depends’?”

“We know the dependencies, Vinnie. The numbers cover a wide temperature range but they’re all at atmospheric pressure. ‘Pressure times Volume‘ makes it easy to adjust for pressure change — just do that multiplication and add the result to the other terms. It’s trickier when the pressure varies between here and there but we’ve got math to handle that. The ‘thermal‘ part’s also not a big problem because if you something’s specific heat you know how its energy content changes with temperature change and vice‑versa.”

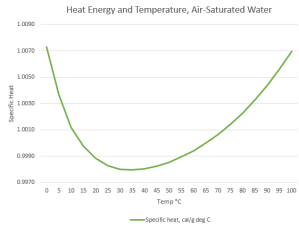
<checking a chart on his phone> “This says water’s specific heat number changes with temperature. They’re all about 1.0 but some are a little higher and some a little lower. Graph ’em out, looks like there’s a pattern there.”

<tapping on Old Reliable’s screen> “Good eye. High at the extreme temperatures, lower near — that’s interesting.”

Data from CRC handbook, 39th Ed, pp 2081-2082

“What’s that?”

“The range where the curve is flattest, 35 to 40°C. Sound familiar?”

“Yeah, my usual body temperature’s in there, toward the high side if I’ve got a fever. What’s that mean?”

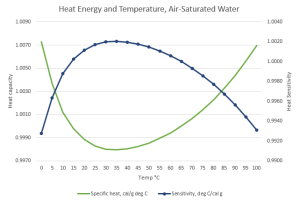
“That’s so far out of my field all I’ve got is guesses. Hold on … there, I’ve added a line for 1/SH.”

“What’s that get you?”

“A different perspective. Specific Heat is the energy change when one gram of something changes temperature by one degree. This new line, I’ve called it Sensitivity, is how many degrees one unit of heat energy will warm the gram. Interesting that both curves flatten out in exactly the temperature range that mammals like us try to maintain. The question is, why do mammals prefer that range?”

“And your answer is?”

“A guess. Remember, I’m not a biologist or a biochemist and I haven’t studied how biomolecules interact with water.”

“I get that we should file this under Crazy Theories. Out with it.”

“Okay. Suppose it’s early days in mammalian evolution. You’re one of those early beasties. You’re not cold-blooded like a reptile, you’re equipped with a thermostat for your warm blood. Maybe you shiver if you’re cold, pant if you’re hot, doesn’t matter. What does matter is, your thermostat has a target temperature. Suppose your target’s on the graph’s coolish left side where water’s sensitivity rises rapidly. You’re sunning yourself on a flat rock, all parts of you getting the same calories per hour.”

“That’s on the sunward side. Shady side not so much.”

“Good point. I’ll get to that. On the sunward side you’re absorbing energy and getting warm, but the warmer you get the more your heat sensitivity rises. Near your target point your tissues warm up say 0.4 degree per unit of sunlight, but after some warming those tissues are heating by 0.6 degrees for the same energy input.”

“I recognize positive feedback when I see it, Sy. Every minute on that rock drives me further away from my target temperature. Whoa! But on the shady side I don’t have that problem.”

“That’s even messier. You’ve got a temperature disparity between the two sides and it’s increasing. Can your primitive circulatory system handle that? Suppose you’re smart enough to scurry out of the sunlight. You’ve still got a problem. There’s more to you than your skin. You’ve got muscles and those muscles have cells and those cells do biochemistry. Every chemical reaction inside you gives off at least a little heat for more positive feedback.”

“What if my thermostat’s set over there on the hot side?”

“You’d be happy in the daytime but you’d have a problem at night. For every degree you chill below comfortable, you need to generate a greater amount of energy to get back up to your target setting.”

“Smart of evolution to set my thermostat where water’s specific heat changes least with temperature.”

“That’s my guess.”

~~ Rich Olcott

Hiding Under Many Guises

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized3 Comments

Vinnie lifts his pizza slice and pauses. “I dunno, Sy, this Pressure‑Volume part of enthalpy, how is it energy so you can just add or subtract it from the thermal and chemical kinds?”

“Fair question, Vinnie. It stumped scientists through the end of Napoleon’s day until Sadi Carnot bridged the gap by inventing thermodynamics.”

“Sounds like a big deal from the way you said that.”

“Oh, it was. But first let’s clear the ‘is it energy?’ question. How would Newton have calculated the work you did lifting that slice?”

“How much force I used times the distance it moved.”

“Putting units to that, it’d be force in newtons times distance in meters. A newton is one kilogram accelerated by one meter per second each second so your force‑distance work there is measured in kilograms times meters‑squared divided by seconds‑squared. With me?”

“Hold on — ‘per second each second’ turned into ‘per second‑squared.” <pause> “Okay, go on.”

“What’s Einstein’s famous equation?”

“Easy, E=mc².”

“Mm-hm. Putting units to that, c is in meters per second, so energy is kilograms times meters‑squared divided by seconds‑squared. Sound familiar?”

“Any time I’ve got that combination I’ve got energy?”

“Mostly. Here’s another example — a piston under pressure. Pressure is force per unit area. The piston’s area is in square meters so the force it feels is newtons per meter‑squared, times square meters, or just newtons. The piston travels some distance so you’ve got newtons times meters.”

“That’s force‑distance work units so it’s energy, too.”

“Right. Now break it down another way. When the piston travels that distance, the piston’s area sweeps through a volume measured in meters‑cubed, right?”

“You’re gonna say pressure times volume gives me the same units as energy?”

“Work it out. Here’s a paper napkin.”

“Dang, I hate equations … Hey, sure enough, it boils down to kilograms times meters‑squared divided by seconds‑squared again!”

“There you go. One more. The Ideal Gas Law is real simple equation —”

“Gaah, equations!”

“Bear with me, it’s just PV=nRT.”

“Is that the same PV so it’s energy again?”

“Sure is. The n measures the amount of some gas, could be in grams or whatever. The R, called the Gas Constant, is there to make the units come out right. T‘s the absolute temperature. Point is, this equation gives us the basis for enthalpy’s chemical+PV+thermal arithmetic.”

“And that’s where this Carnot guy comes in.”

“Carnot and a host of other physicists. Boyle, Gay‑Lussac, Avagadro and others contributed to Clapeyron’s gas law. Carnot’s 1824 book tied the gas narrative to the energetics narrative that Descartes, Leibniz, Newton and such had been working on. Carnot did it with an Einstein‑style thought experiment — an imaginary perfect engine.”

“Anything perfect is imaginary, I know that much. How’s it supposed to work?”

<sketching on another paper napkin> “Here’s the general idea. There’s a sealed cylinder in the middle containing a piston that can move vertically. Above the piston there’s what Carnot called ‘a working body,’ which could be anything that expands and contracts with temperature.”

“Steam, huh?”

“Could be, or alcohol vapor or a big lump of iron, whatever. Carnot’s argument was so general that the composition doesn’t matter. Below the piston there’s a mechanism to transfer power from or to the piston. Then we’ve got a heat source and a heat sink, each of which can be connected to the cylinder or not.”

“Looks straight‑forward.”

“These days, sure. Not in 1824. Carnot’s gadget operates in four phases. In generator mode the working body starts in a contracted state connected to the hot Th source. The body expands, yielding PV energy. In phase 2, the body continues to expand while it while it stays at Th. Phase 3, switch to the cold Tc heat sink. That cools the body so it contracts and absorbs PV energy. Phase 4 compresses the body to heat it back to Th, completing the cycle.”

“How did he keep the phases separate?”

“Only conceptually. In real life Phases 1 and 2 would occur simultaneously. Carnot’s crucial contribution was to treat them separately and yet demonstrate how they’re related. Unfortunately, he died of scarlet fever before Clapeyron and Clausius publicized and completed his work.”

~ Rich Olcott

Energy Is A Shape-shifter

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

Another dinner, another pizza at Eddie’s place. Vinnie wanders over to my table. “Hi, Sy, got a minute?”

“Not doing anything other than eating, Vinnie. What’s on your mind other than the sound of my chewing?”

“At least you keep your mouth closed. No, it’s about this energy thing you’ve gotten back into. I read that enthalpy piece and it’s bothering me.”

“In what way?”

“Well, you said that something’s enthalpy is the energy total of ‘thermal plus Pressure‑Volume plus chemical energy,’ right? I’m trying to fit that together with the potential energy and kinetic energy we talked about a while ago. It’s not working.”

“Deep question for dinner time but worth the effort. Would it help if I told you that the ‘actual versus potential’ notion goes back to Aristotle, the ‘kinetic’ idea came from Newton’s enemy Leibniz, but ‘enthalpy’ wasn’t a word until the 20th century?”

“Not a bit.”

“Didn’t think it would. Here’s another way to look at it. The thinkers prior to the mid‑1700s all looked at lumpy matter — pendulums, rolling balls on a ramp, planets, missiles — either alone or floating in space or colliding with each other. You could in principle calculate kinetic and potential energy for each lump, but that wasn’t enough when the Industrial Revolution came along.”

“What more did they want?”

“Fuel was suddenly for more than cooking and heating the house. Before then, all you needed to know was whether the log pile was stocked better than it was last year. If not, you might have a few chilly early Spring days but you could get past that. Then the Revolution came along. Miners loved Watt’s coal‑fired water‑pump except if you bought one and ran out of coal then the mine flooded. The miners learned that some kinds of coal burned hotter than others. You didn’t need as much of the good kind for a day’s pumping. The demand for a coal‑rating system got the scientists interested, but those lumps of coal weren’t falling or colliding, they just sat there with their heat locked inside. The classical energy quantities didn’t seem to apply so it was time to invent a new kind of energy.”

“That’s how Conservation of Energy works? You just spread the definition out a little?”

“That’s the current status of dark energy, for instance. We know the galaxies are moving apart against gravity so dark energy’s in there to balance the books. We have no good idea why it exists or where it comes from, but we can calculate it. ‘Internal energy’ put the Victorian‑era physicists in the same pickle — ‘atom’ and ‘molecule’ were notions from Greek and Roman times but none of the Victorians seriously believed in them. The notion of chemical bond energy didn’t crop up until the twentieth century. Lacking a good theory, all the Victorians could do was measure and tabulate heat output from different chemical reactions, the data that went into handbooks like the CRC. Naturally they had to invent thermodynamics for doing the energy accountancy.”

“But if it’s just book-balancing, how do you know the energy is real?”

“Because all the different forms of energy convert to each other. Think of a rocket going up to meet the ISS. Some of the rocket fuel’s chemical energy goes into giving the craft gravitational potential energy just getting it up there. At the same time, most of the chemical energy becomes kinetic energy as the craft reaches the 27600 km/h speed it needs to orbit at that altitude.”

<grin> “All?”

“Okay, we haven’t figured out how to harness dark energy. Yet.”

“HAW! Wait, how does enthalpy’s ‘chemical+PV+thermal’ work when the pressure’s zero, like out in space?”

“Then no work was done against an atmosphere up there to make way for the volume. Suppose you suddenly transported a jug of fuel from Earth up to just outside of the ISS. Same amount of fuel, so same amount of chemical energy, right? Same temperature so same thermal component?”

“I suppose.”

“The volume that the jug had occupied on Earth, what happened to it?”

“Suddenly closed in, probably with a little thud.”

“The thud sound’s where the Earth‑side PV energy went. It all balances out.”

~ Rich Olcott

12345 and 8 and 2025

On By rolcottIn General: Fun Stuff, Mathematics, Uncategorized1 Comment

Okay, I’ve got this thing about prime numbers. Some people get all woozy for holiday music as December marches along, but the turning of the year puts me into numeric mode. I’ve done year‑end posts about the special properties of the integer 2016 and integers made up of 3s and 7s. (Sheldon Cooper’s favorite, 73, is just part of an interesting crowd.)

I looked up “2025” in the On-line Encyclopedia of Integer Sequences (the OED of numbers). That number is involved in 1028 different series or families. Sequence A016754, the Central Octagonal Numbers, has some fun visuals. Draw a dot. Then draw eight dots symmetrically around it. You have nine dots. Nine is O2, the second Central Octagonal Number (an octagon enclosing a center, such a surprise). It’s ‘second‘ after O1=1, for that first dot. Now draw another octagon of dots around the core you started, but with two dots on each side. Those 16 dots plus the 9 inside make 25, so O3=25. An octagon with three dots on each side has 24 dots so O4 is 1+8+16+24=49 (see the figure). And so on. If you do the arithmetic, you’ll find that O22, the 22nd Central Octagonal Number, is 2025. Its visual has 22 rings (including the central dot), 168 dots in its outermost ring, for 2025 dots in all.

In case you’re wondering, there is a non-centered series of octagonal numbers that grow out of a dot placed at a vertex of a starter octagon. 2025 isn’t in that series. See the hexagon equivalent in my 2015 post.

Sadly, 2025 isn’t a prime year. Prime‑number years, 2003 and 2011 for example, can be evenly divided by no integer other themselves (and one, of course). 2017 was a prime year, but we won’t see another until 2027. Leap year numbers are divisible by 4 so they can’t ever be prime. That property disqualified 2020 and 2024. It’ll do the same for 2028 and 2032.

Two primes that are as close together as possible, separated only by a single (necessarily even) number, are called twins. There were no twin‑prime years in the 700s, the 900s or the 1500s. The thirteen prime years in the twenty‑first century include three sets of twins, 2027‑2029, 2081‑2083 and 2087‑2089.

If a number’s not prime, then it must be divisible by at least two factors other than itself and one. 2018 and 2019, for example, each have just two factors (2×1009 and 3×673, respectively). Numbers could have more factors, naturally — 2010 is 2×3×5×67 and 2030 is 2×5×7×29, four factors each.

A single factor could be used multiple times — 2024 is 2×2×2×11×23, also written as 23×11×23, for a total of 5 factors. We’re just entering a 6‑factor year (see below) but a formidable factor‑champion is on the horizon. Computer geeks may be particularly fond of the year 2048, known in the trade as 2k (not to be confused with Y2K). The number 2048 has eleven factors, more than any year number of last or this millennium. 2048 is 211, the result of eleven 2s multiplied together. Change just one of those 2s to a 3 and you have 3072 which is a long time from now.

So anyhow, I was poking at 2025, just seeing what was in there. The 5 at the tail‑end is a dead give‑away non‑prime‑wise because the only prime that ends in a 5 is … 5. Another useful trick – add up the digits. If the sum is divisible by 3, so is the number. If the sum is divisible by 9 so is the number. Easy to figure 2+0+2+5=9, so two easy ways to know that 2025‘s not prime.

By the time I got done breaking the number down into all six of its factors, look what a pretty pattern appeared:

Finally, 2025 appears 8 times in this post’s text. Happy New Year.

~~ Rich Olcott

The Trough And The Plateau

On By rolcottIn Astronomy: Planetary Science, Mathematics, UncategorizedLeave a comment

Particularly potent pepperoni on Pizza Eddie’s special tonight so I dash to the gelato stand. “Two dips of pistachio in a cup, please, Jeremy, and hurry. Hey, why the glum look?”

“The season’s moving so slowly, Mr Moire. I’m a desert kid, used to bright skies. I need sunlight! We’re getting just a few hours of cloudy daylight each day. It seems like we’re never gonna leave this pattern. Here’s your gelato.”

“Thanks. Sorry about the cloudiness, it’s the wintertime usual around here. But you’re right, we’re on a plateau.”

“Nosir, the Plateau’s the Four Corners area, on the other side of the Rockies, miles and miles away from here.”

<chuckle> “Not the Colorado Plateau, the darkness plateau. Or the daylight trough, if you prefer. Buck up, we’ll get a daylight plateau starting in a few months.” <unholstering Old Reliable> “Here’s a plot of daylight hours through the year at various northern latitudes. We’re in between the red and green curves. For folks south of the Equator that’d just turn upside‑down, of course. I added a star at today’s date in mid‑December, see. We’re just shy of the winter solstice; the daylight hours are approaching the minimum. You’re feeling stressed because these curves don’t change much day-to-day near minimum or maximum. In a couple of weeks the curve will bend upwards again. Come the Spring equinox, you’ll be shocked at how rapidly the days lengthen.”

“Yeah, my Mom says I’m too impatient. She says that a lot. Okay, above the Arctic Circle they’ve got months‑long night and then months‑long day, I’ve read about that. I hadn’t realized it was a one‑day thing at the Circle. Hey, look at the straight lines leading up to and away from there. Is that the Summer solstice? Those low‑latitude curves look like sine waves. Are they?”

“Summer solstice in the northern hemisphere, Winter solstice for the southerners. The curves are distorted sines. Ready for a surprise?”

<Looks around the nearly empty eatery.> “With business this slow I’m just sitting here so I’m bored. Surprise me, please.”

“Sure. One of the remarkable things about a sine wave is, when you graph its slopes you get another sine wave shifted back a quarter. Here, check it out.”

“Huh! When the sine wave’s mid-climb, the slope’s at its peak. When the sine wave’s peaking, the slope’s going through zero on the way down. And they do have exactly the same shape. I see where you’re going, Mr Miore. You’re gonna show me the slopes of the daylight graphs to see if they’re really sine waves.”

“You’re way ahead of me and Old Reliable, Jeremy.” <frantic tapping on OR’s screen> “There, point‑by‑point slopes for each of the graphs. Sorta sine‑ish near the Equator but look poleward.”

“The slopes get higher and flatter until the the Arctic Circle line suddenly drops down to flip its sign. Those verticals are the solstices, right?”

“Right. Notice that even at the Circle the between‑solstice slopes aren’t quite constant so the straight lines you eye‑balled aren’t quite that. North of the Circle the slopes go nuts because of the abrupt shifts between varying and constant sun.”

Link to larger image

“How do you get these curves, Mr Moire?”

“It’s a series of formulas. Dust off your high school trig. The Solar Declination Angle equation is about the Sun’s height above or below the horizon. It depends on Earth’s year length, its axial tilt and the relative date, t=T‑T0. For these charts I set T0 to the Spring equinox. If the height’s negative the Sun’s below the horizon, okay?”

“Sine function is opposite‑over‑hypotenuse and the height’s opposite alright or we’d burn up, yup.”

“The second formula gives the the Hour Angle between your longitude and whichever longitude has the Sun at its zenith.”

“Why would you want that?”

“Because it’s the heart of the duration formula. When you roll all three formulas together you get one big expression that gives daylight duration in terms of Earth’s constants, time of year and your location. That’s what I plotted.”

“How about the slope curves?”

“Calculus, Jeremy, d/dt of that combined duration function. It’s beyond my capabilities but Old Reliable’s up to it.”

~ Rich Olcott

New (Old) Word: Frigorific!

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

A quiet morning at Cal’s Coffee. I’m sipping my morning mud when Susan Kim bustles to my table, mocha latte in hand. “There you are, Sy. I loved your posts in tribute to the well‑thumbed copy of the CRC Handbook on my desk.”

“Glad you enjoyed them.”

“Your Rumford stuff made it even better because I did a class report on him once so I caught your ‘frigorific‘ reference. What do you know about the background to that?”

“Not much. Didn’t sound like a real word when I ran across it.”

“Oh, it’s a real word but it has a technical meaning now that it didn’t in Newton’s time. Back then it was only about making something cold. These days we also use the word for a mixture that maintains a dependable cold temperature. Liquid water and ice, for instance, stays at 0°C as long as there’s still ice in the cold bath. I used to use an ammonium chloride/water frigorific when I needed something down around -15°C. Now of course I use a benchtop refrigerator.”

“Rumford would have liked that. What were the ‘frigorific rays‘ he got all excited about?”

“Long story but there’s a couple of fun twists. Background first. At the end of the 1700s there was a <grin> heated debate about heat. The phlogiston theory was dead by that time but people still liked the idea that heat was a material fluid. It addressed some chemical puzzles but heat transmission was still mysterious. Everyone knew that a hot object gives off heat by radiation, that the radiation travels in straight lines and that it’s reflected by metal mirrors.”

“Right, the Greeks are supposed to have used huge sun‑focusing mirrors to burn up attacking Roman ships.”

“Maybe. Anyhow, those properties connected heat with light. However, a pane of glass blocks radiated heat, at least until the glass gets hot. People argued this meant heat and light weren’t connected. About 1790 a group of physicists loosely associated with the Academy of Geneva dove into the fray. Rumford was in the group, along with Prévost, Saussure and his student Pictet. They had lots of fun with heat theories and experiments. One of Pictet’s experiments lit Rumford’s fire, so to speak.”

“Good one.”

<smile> “It’s a fairly simple setup that a high school science teacher could do. Pictet hung a concave metallic mirror facing down from the ceiling of a draft‑free room. He placed another concave metallic mirror at floor level immediately beneath it, facing upward. He probably used spherical mirrors which are easy to make, but they could have been elliptical or parabolic sections. Anyhow, he put a thermoscope at the upper mirror’s focal point and a hot object at the lower focal point. Sure enough, the upper focal point got hotter, just as you’d expect.”

“No great surprise, the Greeks would have expected that, too.”

“The surprise happened when he put a cold object in there. The thermoscope’s droplet moved in the cold direction.”

“Wait, like anti‑infrared?”

“That’s the effect. Wave‑theory supporter Rumford took that thought, called it ‘frigorific radiation‘ and ran with it. He constructed a whole thesis around cold waves and heat waves as symmetric partners. He maintained wave intensity, both kinds, increases with temperature difference. Our heat sources are hundreds or thousand of degrees hotter than we are but our cold sources are at most a few dozen degrees colder. By his theory that’s why cold wave phenomena are masked by heat waves.”

“Give me a minute. … Ah, got it. The very meaning of a focal point is that all waves end or start there. A cold object at the sending station emits much less infrared than the warm object did. The thermoscope bulb now gets less than it emits. With less input from below its net energy drops. It chills.”

“Nice, Sy. Now for the other twist. Rumford published his theory in 1805. Herschel had already identified infrared radiation in the Sun’s spectrum in 1800. Two strikes against Herschel, I guess — he was British and he was an astronomer. Continental physicists wouldn’t bother to read his stuff.”

~ Rich Olcott

Rumford’s Boring Story

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Okay, Mr Moire, my grandfather’s engineering handbook has Specific Heat tables because Specific Heat measures molecular wabbling. If he’s got them, though, why’s Enthalpy in the handbook, too?”

“Enthalpy’s not my favorite technical term, Jeremy. It’s wound up in a centuries‑old muddle. Nobody back then had a good, crisp notion of energy. Descartes, Leibniz, Newton and a host of German engineers and aristocratic French hobby physicists all recognized that something made motion happen but everyone had their own take on what that was and how to calculate its effects. They used a slew of terms like vis viva, ‘quantity of motion,’ ‘driving force,’ ‘quantity of work,’ a couple of different definitions of ‘momentum‘ — it was a mess. It didn’t help that a lot of the argument went on before Euler’s algebraic notations were widely adopted; technical arguments without math are cumbersome and can get vague and ambiguous. Lots of lovely theories but none of them worked all that well in the real world.”

“Isn’t that usually what happens? I always have problems in the labs.”

“You’re not alone. Centuries ago, Newton’s Laws of Motion and Gravity made good predictions for planets, not so good for artillery trajectories. Gunners always had to throw in correction factors because their missiles fell short. Massachusetts‑born Benjamin Thompson, himself an artilleryman, found part of the reason.”

“Should I know that name?”

“In later years he became Count Rumford. One of those people who get itchy if they’re not creating something. He was particularly interested in heat — how to trap it and how to make it go where you want.”

“Wait, he was an American but he was a Count? I thought that was illegal.”

“Oh, he left the States before they were the States. During the Revolution he organized a Royalist militia in New York and then lit out for Europe. The Bavarians made him a Count after he spent half‑a‑dozen years doing creative things like reorganizing their army, building public works and introducing potato farming. He concocted a nourishing soup for the poor and invented the soup line for serving it up. But all this time his mind was on a then‑central topic of Physics — what is heat?”

“That was the late 1700s? When everyone said heat was some sort of fluid they called ‘caloric‘?”

“Not everyone, and in fact there were competing theories about caloric — an early version of the particle‑versus‑wave controversy. For a while Rumford even supported the notion that ‘frigorific’ radiation transmitted cold the same way that caloric rays transmitted heat. Whatever, his important contributions were more practical and experimental than theoretical. His redesign of the common fireplace was such an improvement that it took first England and then Europe by storm. Long‑term, though, we remember him for a side observation that he didn’t think important enough to measure properly.”

“Something to do with heat, I’ll bet.”

“Of course. As a wave theory guy, Rumford stood firmly against the ‘caloric is a fluid‘ camp. ‘If heat is material,‘ he reasoned, ‘then a heat‑generating process must eventually run out of caloric.’ He challenged that notion by drilling out a cannon barrel while it was immersed in cold water. A couple of hours of steady grinding brought the water up to boiling. The heating was steady, too, and apparently ‘inexhaustible.’ Better yet, the initial barrel, the cleaned‑out barrel and the drilled‑out shavings all had the same specific heat so no heat had been extracted from anything. He concluded that heat is an aspect of motion, totally contradicting the leading caloric theories and what was left of phlogiston.”

<chuckle> “He was a revolutionary, after all. But what about ‘Enthalpy‘?”

“Here’s an example. Suppose you’ve got a puddle of gasoline, but its temperature is zero kelvins and somehow it’s compressed to zero volume. Add energy to those waggling molecules until the puddle’s at room temperature. Next, push enough atmosphere out of the way to let the puddle expand to its normal size. Pushing the atmosphere takes energy, too — the physicists call that ‘PV work‘ because it’s calculated as the pressure times the volume. The puddle’s enthalpy is its total energy content — thermal plus PV plus the chemical energy you get when it burns.”

~~ Rich Olcott

It’s in The Book

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, Physics: Quantum Mechanics, UncategorizedLeave a comment

A young man’s knock, eager yet a bit hesitant. “Door’s open, Jeremy, c’mon in.”

“Hi, Mr Moire, I’ve got something to show you. It’s from my acheii, my grandfather. He said he didn’t need it any more now he’s retired so he gave it to me. What do you think?”

“Wow, the CRC Handbook of Chemistry And Physics, in the old format, not the 8½×11″ monster. An achievement award, too — my congratulations to your grandfather. Let’s see … over 3000 pages, and that real thin paper you can read through. It’s still got the math tables in front — they moved those to an Appendix by the time I bought my copy. Oooh yeah, lots of data in here, probably represents millions of grad student lab hours. Tech staff, too. And then their bosses spent time checking the work before publishing.”

“Acheii said I’d have to learn a lot before I could use it properly. I see lots of words in there I don’t recognize.” <opens book to a random page> “See, five- and six‑figure values for, what’re Specific Heat and Enthalpy?”

“Your grandfather’s absolutely correct. Much of the data’s extremely specialized. Most techs, including me, have a few personal‑favorite sections they use a lot, never touch the rest of the book. These particular pages, for instance, would be gold for a someone who designs or operates steam‑driven equipment.”

“But what do these numbers mean?”

“Specific Heat is the amount of heat energy you need to put into a certain mass of something in order to raise its temperature by a certain amount. In the early days the Brits, the Scots really, defined the British Thermal Unit as the amount of energy it took to raise the temperature of one pound of liquid water by one degree Fahrenheit. You’d calculate a fuel purchase according to how many BTUs you’d need. Science work these days is metric so these pages tabulate Specific Heat for a substance in joules per gram per °C. Tech in the field moves slow so BTUs are still popular inside the USA and outside the lab.”

“But these tables show different numbers for different temperatures and they’re all for water. Why water? Why isn’t the Specific Heat the same number for every temperature?”

“Water’s important because most power systems use steam or liquid water as the working fluid or coolant. Explaining why heat capacity varies with temperature was one of the triumphs of 19th‑century science. Turns out it’s all about how atomic motion but atoms were a controversial topic at the time. Ostwald, for instance—”

“Who?”

“Wilhelm Ostwald, one of science’s Big Names in the late 1800s. Chemistry back then was mostly about natural product analysis and seeing what reacted with what. Ostwald put his resources into studying chemical processes themselves, things like crystallization and catalysis. He’s regarded as the founder of Physical Chemistry. Even though he invented the mole he steadfastly maintained that atoms and molecules were nothing more than diffraction‑generated illusions. He liked a different theory but that one didn’t work out.”

“Too bad for him.”

“Oh, he won the first Nobel Prize in Chemistry so no problem. Anyway, back to Specific Heat. In terms of its molecules, how do you raise something’s temperature?”

“Um, temperature’s average kinetic energy, so I’d just make the molecules move faster.”

“Well said, except in the quantum world there’s another option. The molecules can’t just waggle any which way. There are rules. Different molecules do different waggles. Some kinds of motion take more energy to excite than others do. Rule 1 is that the high‑energy waggles don’t get to play until the low‑energy ones are engaged. Raising the temperature is a matter of activating more of the high‑energy waggles. Make sense?”

“Like electron shells in an atom, right? Filling the lowest‑energy shells first unless a photon supplies more energy?”

“Exactly, except we’re talking atoms moving within a molecule. Smaller energies, by a factor of 100 or more. My point is, the heat capacity of a substance depends on which waggles activate as the temperature rises. We didn’t understand heat capacity until we applied quantum thinking to the waggles.”

“What about ‘Enthalpy’ then?”

Crystal photo by JJ Harrison

~ Rich Olcott

Behold, a square?

On By rolcottIn General: Fun Stuff, Uncategorized1 Comment

It’s been a while since I heard that footstep in the hall outside my office. “Door’s open, Vinnie, c’mon in.”

“Hi, Sy. Brought you a thing.” <lays a card on my desk> “So the question is, how is this a square?”

“Is this another puzzle you got from Larry?”

“Yeah. He said you could ‘splain it.”

“Well, the idea’s clear — four right angles, four equal sides, sounds square-ish to me.”

“Yeah, but is the picture lying to us the way that other one did?”

“Fair question. Let’s see whether we can construct it with some real numbers. Both of those arcs seem to be parts of concentric circles so I’ll assume that.” <drawing on card> “The one that’s most of a circle has a radius I’ll call r.”

“You’re gonna do equations, ain’t you? You know I hate equations.”

“You asked the question. Bear with me, this won’t take long. Those two straight lines seem to run radially out from the almost‑circle’s center. I’ll call the angle between them a. By the way, if the lines are indeed radial then we’re guaranteed that all four of those ‘right angle’ markers are truthful. Any radius meets its circumference in a right angle, right?”

“Learned that in Geometry class.”

“I certainly hope so. Okay, the radius of the outer arc is 1 plus the radius of the inner arc so the length of the outer arc is the angle times that or a(1+r) —”

“Wait, where did that come from? You can’t just multiply the angle and radius together like that.”

“Sure you can. What’s the formula for a circle’s circumference?”

“2πr.”

“Which is an angle, 2π, times the radius.”

“How is 2π an angle? Should be 360°.”

“It’s like feet and meters ‑ same value, different units. Physicists like radians. 180° is π radians and the length of a semicircle is πr. Other arcs work the same way. It’s perfectly legal to multiply angle and radius if you express the angle in radians. So that outer arc length is a(1+r) and that’s 1 according to the diagram. Are you with me?”

“I suppose.”

“Now for the almost‑circle. Its angle is 2π minus that bit that got stretched out. Are we agreed that the arc length is (2π-a)r?”

“And that’s also 1.”

“Right. So we have two unknowns a and r, and two equations to settle them with: a(1+r)=1 and (2π-a)r=1. Simple high school algebra but I’ll spare you the pain and just ask Old Reliable for the result.”

“Thank you.”

“So there’s your answer. Yes, the keyhole figure can be truthful if the angle is 48.4° and the sticky‑out part is about 5½ times longer than the almost‑circle’s radius. Any other angle or radius and the diagram’s wrong. Happy?”

“Yeah.” <quiet moment> “Hey, I just figured out a different way. The latitude lines and longitude lines always cross at right angles, right?”

“Right.”

“So you could do a keyhole ‘square’ on the Earth, right? Circle the North Pole at some latitude, except take a detour straight south, then straight west for a while, then straight back north just in time to meet your part‑circle’s starting point. I’ve flown crazy routes a little like that but that’s always been point‑to‑point. How do you from‑scratch figure something like that so that all the sides are the same length?”

“Whoa, that’s a much harder problem. You’re flying over Earth’s surface so r is constant but now you’ve got two angular variables, latitude and longitude. The north‑south tracks are pretty straight‑forward — you’re good if one starts at the same latitude the other stops at. The tough part is how to split the 360° of longitude between the two east‑west tracks so that the southern arc is the same length as the northern one and they both match the north‑south distance which depends on the start‑stop latitudes. That’s not quadratic equations any more, we’re looking at transcendental equations involving trig functions. There may not be a closed‑form solution. To get those angles we’d need a load of computer time doing successive approximations toward a numerical solution. Surely keyhole‑square routes exist but they’re well‑hidden.”

“Regular squares’re much easier. Colorado or Wyoming’d be no problem.”

~~ Rich Olcott

Not Enough Monkeys

On By rolcottIn General: Fun Stuff, UncategorizedLeave a comment

“Morning, Sy. You see the news about the Infinite Monkey thing?”

“No, Cal, with everything else going on I seem to have missed that.”

“Understandable. I only heard about it from a ‘lighter side of the news’ piece on the radio. Something about disproving what everybody used to believe. You wrote about it a while ago, didn’t you?”

“Mm-hm. Did a lot of arithmetic for that one. The idea is that if you somehow managed to get an infinite number of monkeys banging away on typewriters, sooner or later one of them would produce the complete works of Shakespeare. The piece I did, gee, years ago, used Terry Pratchett’s idea of a library that contains all the books that have been written, all those that will be written, and all those that would have been written but the author thought better of it. I asked, how big is that library?”

“That’s gotta be a lot of books. Here’s your coffee.”

“Thanks. I guessed maybe a billion, maximum. The Library of Congress has only 30‑some million, last I looked, and that’s real books. Anyhow, I decided to compare that to the number of possible books, printed up using some configuration of 500 characters.”

“500? What else besides ‘a, b, c‘?”

“Upper case, lower case, blanks, punctuation, math symbols, alphabets from other languages, whatever. No pictographic systems like Japanese kanji and Chinese but you can’t have everything. I defined ‘possible book’ as 500 pages, 4000 characters per page so two million per book.”

“All my books are shorter than that and they don’t scramble alphabets from different languages.”

“Short books you could pad to 500 characters with blanks at the end. Some of the experimental fanfic I’ve seen is pretty creative. At any rate, I calculated 5002,000,000 = 105,397,940 different possible books. Limit the library to 250 pages and 100 characters in, say, Spanish with no math that’d be 1001,000,000 = 102,000,000 different possible books, which is still huge, right?”

“My calculator doesn’t do numbers up in the air like that. I’ll believe you, it’s a big number. So where are you going with this?”

“So even a billion‑book library would be swamped by the other 105,397,931 books in an all‑possible‑books library. My point in that old post was that the monkeys could indeed type up Shakespeare but you wouldn’t be able to find it in the welter of absolute nonsense books.”

He’s an Ape, not a monkey

“Looks good to me, so what’d these guys prove?”

“Dunno, haven’t seen their paper yet. Give me a minute with Old Reliable … Ah, here it is, ‘A numerical evaluation of the Finite Monkeys Theorem‘ by Woodcock and Falletta. Aand it’s not paywalled!” <reading> “Wait, finite — that’s different.”

“How’s it different? Arithmetic’s arithmetic, right?”

“Until you get into infinities. True infinity operates differently than ‘large beyond anything we can measure’. I highlighted the difference in a tech note I wrote a few years ago. How would you bet if someone suggested there’s an exact duplicate Earth existing somewhere else in the Universe?”

“That’s what that goofy ‘Everything Everywhere’ movie was all about, right? Multiverses?”

“Mmm, no, the bet’s about only in our Universe.”

“Knowing you, I’d stay out of the betting.”

“Wise choice. The right answer is ‘It depends’. I calculated that there could be 1.54×10154 possible Earths with exactly the same atom count that we have, just arranged differently, maybe swap one nickel atom with one iron atom inside a hematite rock. So 1.54×10154 chances for an identical copy of you. If the Universe is infinite, then you’re guaranteed to have not just one, but an infinite number of identical copies, each of whom thinks they’re the only you.”

“That’s comforting, somehow.”

“On the other hand, if the Universe is finite, then the planet creation process would have to run through something like 10150 creations before it had a good shot at re‑making you. Vanishingly small odds.”

“So what’s this got to do with finite monkeys?”

“Woodcock and Falletta maintain that there’s only a limited number of monkeys and they’re time‑constrained. Under those conditions, there’s vanishingly small odds for Shakespeare or even the word ‘bananas’.”

~ Rich Olcott