Tag: Cathleen

Mushy stuff

On By rolcottIn Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

“Amanda! Amanda! Amanda!”

“All right, everyone, settle down for our final Crazy Theorist. Jim, you’re up.”

“Thanks, Cathleen. To be honest I’m a little uncomfortable because what I’ve prepared looks like a follow-on to Newt’s idea but we didn’t plan it that way. This is about something I’ve been puzzling over. Like Newt said, black holes have mass, which is what everyone pays attention to, and charge, which is mostly unimportant, and spin. Spin’s what I’ve been pondering. We’ve all got this picture of a perfect black sphere, so how do we know it’s spinning?”

Voice from the back of the room — “Maybe it’s got lumps or something on it.”

“Nope. The No-hair Theorem says the event horizon is mathematically smooth, no distinguishing marks or tattoos. Question, Jeremy?”

“Yessir. Suppose an asteroid or something falls in. Time dilation makes it look like it’s going slower and slower as it gets close to the event horizon, right? Wouldn’t the stuck asteroid be a marker to track the black hole’s rotation?”

“Excellent question.” <Several of Jeremy’s groupies go, “Oooh.”> “Two things to pay attention to here. First, if we can see the asteroid, it’s not yet inside the horizon so it wouldn’t be a direct marker. Beyond that, the hole’s rotation drags nearby spacetime around with it in the ergosphere, that pumpkin‑shaped region surrounding the event horizon except at the rotational poles. As soon as the asteroid penetrates the ergosphere it gets dragged along. From our perspective the asteroid spirals in instead of dropping straight. What with time dilation, if the hole’s spinning fast enough we could even see multiple images of the same asteroid at different levels approaching the horizon.”

Jeremy and all his groupies go, “Oooh.”

“Anyhow, astronomical observation has given us lots of evidence that black holes do spin. I’ve been pondering what’s spinning in there. Most people seem to think that once an object crosses the event horizon it becomes quantum mush. There’d be this great mass of mush spinning like a ball. In fact, that was Schwarzchild’s model for his non-rotating black hole — a simple sphere of incompressible fluid that has the same density throughout, even at the central singularity.”

VBOR — “Boring!”

“Well yeah, but it might be correct, especially if spaghettification and the Firewall act to grind everything down to subatomic particles on the way in. But I got a different idea when I started thinking about what happened to those two black holes that LIGO heard collide in 2015. It just didn’t seem reasonable that both of those objects, each dozens of solar masses in size, would get mushed in the few seconds it took to collide. Question, Vinnie?”

“Yeah, nice talk so far. Hey, Sy and me, we talked a while ago about you can’t have a black hole inside another black hole, right, Sy?”

“That’s not quite what I said, Vinnie. What I proved was that after two black holes collide they can’t both still be black holes inside the big one. That’s different and I don’t think that’s where Jim’s going with this.”

“Right, Mr Moire. I’m not claiming that our two colliders retain their black hole identities. My crazy theory is that each one persists as a high‑density nubbin in an ocean of mush and the nubbins continue to orbit in there as gravity propels them towards the singularity.”

VBOR —”Orbit? Like they just keep that dance going after the collision?”

“Sure. What we can see of their collision is an interaction between the two event horizons and all the external structures. From the outside, we’d see a large part of each object’s mass eternally inbound, locked into the time dilation just above the joined horizon. From the infalling mass perspective, though, the nubbins are still far apart. They collide farther in and farther into the future. The event horizon collision is in their past, and each nubbin still has a lot of angular momentum to stir into the mush. Spin is stirred-up mush.”

Cathleen’s back at the mic. “Well, there you have it. Amanda’s male-pattern baldness theory, Newt’s hyper‑planetary gear, Kareem’s purple snowball or Jim’s mush. Who wins the Ceremonial Broom?”

The claque responds — “Amanda! Amanda! Amanda!”

~ Rich Olcott

A Big Purple Snowball

On By rolcottIn Astronomy: Planetary Science, Crazy Theories, UncategorizedLeave a comment

Cathleen’s back at the mic. “Okay, folks, now for the third speaker in tonight’s Crazy Theory seminar. Kareem, you have the floor.”

“Thanks, Cathleen. Some of you already know I do old‑rock geology. If a rock has a bone in it, I’m not interested. Paleontology to me is like reading this morning’s newspaper. So let me take you back to Precambrian times when Earth may have been purple.”

Kareem’s a quiet guy but he’s got the story‑teller’s gift, probably honed it at field expedition campfires, so we all settle back to listen.

“Four and a half billion years ago, Earth was bright orange. That’s not the color it reflected, that’s the color it glowed. You’ve all seen glass‑blowers at work, how the material gives off a bright orange light coming out of the flame or furnace, soft and ready to be formed. That’s what the planet’s surface was like after its Moon‑birthing collision with Theia. Collisions like that release so much heat that there’s no rocks, just layers of smooth molten glassy slag floating on fluid silicates and nickel‑iron like in a blast furnace. No atmosphere, all the volatiles have been boiled off into space. Got the picture?”

General nodding, especially from maybe‑an‑Art‑major who’s good at pictures.

“Time passes. Heat radiating away cools the world from the outside inward. Now the surface is a thin glassy cap, black like obsidian and basalt, mostly smooth. The cooling contracting cap fractures from the tension while the shrinking interior pulls inward, slow but not gentle. The black glassy surface becomes low craggy mountains and razor‑rubble, sharp enough to slice hiking boots to ribbons. There’s no erosive wind or water yet to round things off. Everything stays sharp‑edged.”

Voice from the back of the room — “Where’s our water from then?”

Juno photo of Jupiter’s clouds Credits: NASA/JPL‑Caltech/SwRI/MSSS/Gerald Eichstädt /Seán Doran © CC NC SA

“Good question. Could be buried water that never got the chance to escape past the cap, could be water ferried in on icy comets or worldlets. People argue about it and I’m not taking sides. The planet gets a new color after it cools enough to hold onto water molecules however they got there — but that water doesn’t stay on the surface. Raindrops hitting still‑hot rock hiss back into steamy clouds. If you were on the moon at the time you’d see a white‑and‑grey Earth like Jupiter’s curdled cloud-tops. Visualize a series of million‑year Hurricane Debbies, all over the world.”

He pauses to let that sink in.

“When things finally cool down enough to allow surface water there’s oceans, but they’re not blue. Millions of years of wind and water erosion have ground the sharp rubble to spiky dust. Most of the thrust‑raised mountains, too. Much of the dust is suspended or dissolved in the ocean turning it black. For a while. The dust is loaded with minerals, especially sulfides, very nutritious for a group of not‑quite bacteria called Archaea that eat sulfides using a molecule that’s powered by green light but reflects red and blue. When the Archaea take over, the oceans look magenta from the reflected red and blue.”

Maybe‑an‑Art‑major giggles.

“Next major event, we think, was the Huronian Glaciation, when most or all of the Earth was a solid white because it was covered with ice. Killed off most or the Archaea. When that melted, different parts of the ocean turned black from floating dead Archaea and and then milky turquoise from sulfur particles. Next stage was purple, from a different group of sulfur‑eating purple almost‑bacteria. Then we had snowball whiteness again, which gave green‑reflecting chlorophyll‑users a chance to take over, clear our the sulfur and leave the oceans blue.”

VBOR — “That’s your Crazy Theory?”

“No, that’s mostly mainstream. Question is, what terminated the deepfreezes? Lots of ideas out there — solar dimming and brightening, different combinations of CO2 and methane from volcanoes or bacteria, even meteorites. Anyone remember Ian Malcom’s repeated line in the Jurassic Park movies?”

Everyone — “Life will find a way!”

“Right on. My crazy’s about the two almost‑bacteria. Suppose each kind managed to infiltrate their day’s Great Extinction glaciers. Suppose planet‑wide bacterial purple pigments absorbed sunlight’s energy, melting the ice. Karma, yes?”

~ Rich Olcott

A Great Big Mesh

On By rolcottIn Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

Cal has my coffee mug filled as soon as I step into his shop. “Get to the back room quick, Sy. Cathleen’s got another Crazy Theories seminar going back there.”

So I do. First thing I hear is Amanda finishing her turn at the mic. “And that’s why humans evolved male pattern baldness.”

A furor of “Amanda! Amanda! Amanda!” then Cathleen regains control. “Thank you, Amanda. Next up — Newt Barnes. What’s your Crazy Theory, Newt?”

“Crazy idea, not a theory, but I like it. Everybody’s heard of black holes, right?”

<general nodding>

“And we’ve all heard that nothing can leave a black hole, not even light.”

<more nodding>

“Well in fact that’s mostly not true. There’s so much confusion about black holes. We’ve known about a black hole’s event horizon and its internal mass since the 1920s. It took years for us to realize that the central mass could wrap a shiny accretion disk around itself, and an ergosphere, and maybe spit out jets. So, close outside the Event Horizon there’s a lot of light‑emitting structure, right?”

<A bit less nodding, but still.>

“Right. So I’ll skip in past a few controversial layers and get down to the famously black event horizon. Why’s it black?”

Voice from the back of the room — “Because photons can’t get out because escape velocity’s faster than lightspeed.”

“That’s the answer I expected, but it’s also one of the confusing parts. You’re right, the horizon marks the level where outward‑bound massy particles can’t escape. The escape velocity equation depends on trading off kinetic and gravitational potential energy. Any particle with mass would have to convert an impossible amount of kinetic energy into gravitational potential energy to get through the barrier. But zero‑mass particles, photons and such, are pure kinetic energy. They aren’t bound by a gravitational potential so escape velocity trade‑offs simply don’t apply. There’s a deeper reason photons also can’t get out.”

VBOR — “So what’s trapping them?”

“Time. It traps photons and any kind of information. The other thing about the Event Horizon is, it’s the level where spacetime is so bent around that the time‑coordinate is just on the verge of pointing inward. Once you’re inside that boundary the cause‑and‑effect arrow of time is against you. Whatever direction you point your flashlight, its beam will emerge in your future and that’s away from the horizon. Trying to send a signal outside would be like sending it into your past, which you can’t do. Nothing gets away from a black hole except…”

“Except?”

“Roger Penrose found a loophole and I may have found another one. There’s something that Wheeler called the No-Hair Theorem. It says that the Event Horizon hides everything inside it except for its mass, electric charge and angular momentum.”

“How do those get out?”

“They don’t get out so much as serve as backdrop for all the drama in the rest of the structure. If you know the mass, for instance, you can calculate its temperature and the Horizon’s diameter and a collection of other properties.”

Cathleen senses a teachable moment and breaks in. “Talk about charge and spin, Newt.”

“I was going there, Cathleen. Kerr and company’s equations take account of both of those. Turns out the attractive forces between opposite charges are so much stronger than gravity that it’s hard for an object in space to build up a significant amount of either kind of charge without getting neutralized almost immediately. Kind of ironic that the Coulomb force, far stronger than gravity, generates net energy contributions that are much smaller than the gravity‑based ones. Spin, though, that’s where the loopholes are. Penrose figured out how particles from the accretion disk could dip into the black hole’s spinning ergosphere, steal some of its energy, and stream up to power the jets.”

VBOR — “What’s your loophole then?”

“Speed contrast between layers. The black hole mass is spinning at a great rate, dragging nearby spacetime and the ergosphere and the accretion disk around with it. But the layers go slower as you move outward. Station a turbine generator like an idler gear between any two layers and you’re pulling power from the black hole’s spin.”

Silence … then, “Amanda! Amanda! Amanda!”

~ Rich Olcott

A.I. and The Ouroboros Effect

On By rolcottIn General: Serious Stuff, UncategorizedLeave a comment

The Acme Building Science and Pizza Society is meeting again around the big table near the kitchen in Eddie’s Pizza Place. It’s my deal so I set the next topic. “Artificial Intelligence.” There’s some muttering but play starts.

Cal has first honors. “Not my favorite thing. I hadda change my name ’cause of A.I., f’crying out loud.”

Eddie antes up a chip. “But Cal, your astronomy magazines are loaded with new discoveries that some A.I. made rummaging through godzillabytes of big telescope data. Train an A.I. on a few thousand normal galaxies and then let it chase through the godzillabytes. It says ‘Here’s a weird one‘ and the human team gets to publish papers about a square galaxy or something.”

Susan chips in. “What about all the people who’ve been saved from cancer because an A.I. found bad cells while screening histology images?”

Kareem folds. “Not much A.I. in Geology yet. Our biggest Big Data project these days is whole‑Earth tomography. That uses pretty much all the computer time we can get funds for. A.I.’s Large Language Models soak up all the research money.”

Vinnie raises by a chip. “I use autopilot a lot when I’m flying, but that’s up in the air, Great Circle point‑to‑point and no worries about pedestrian traffic. Autopilot in a car? Not for me, thanks — too many variables and I’ve seen too many crazy situations you couldn’t predict. Black ice in the winter, roadwork and bicyclists the rest of the year — I want to be able to steer and brake when I need to.”

Susan grins. “Are you a stick‑shift purist, Vinnie?”

“Naw, automatic transmissions are okay these days and besides my car uses electric motors and doesn’t even have a transmission. Lots of torque at low revs and that’s the way I like it. What about you, Cathleen? Got any A.I. war stories?”

Cathleen calls Vinnie’s raise. “A few. One thing I’ve learned — chatbots have a limited working memory. I once asked a bot to list Jupiter’s 35 biggest moons in decreasing order of size. It got the first 24 in the right order, then some more moons out of order and two of them were moons of Saturn. So ‘trust but verify‘ like the man said. Sy, you do a lot of writing. What’s your experience?”

I call Cathleen’s raise. “Mixed. I’m a generalist so I have to read a lot of papers or at least be aware of them. Summarizer bots do a decent job on some reports but miss badly when it comes to tying together material that’s not already well organized. Probably comes from that working memory limitation you noticed, Cathleen. The other problem I’ve seen doesn’t apply so much to technical work but it’s a killer for essays and fiction that have anything to do with interactions between people.”

“I’ve seen that, too. No soul.”

“Soul’s the word I’ve been looking for, Kareem. The bots are good at picking up styles and ‘who said what‘ surface material, but they fail completely at emotional subtext, the ‘why‘ that’s the actual thread of a conversation. Subtext is why we read good novels. From what I’ve been seeing recently, it’s not going to get any better.”

“Nothing does, I’m starting to think.”

“C’mon, Cal, your coffee’s improved since the city put in better water pipes. On the other hand, you owe the pot a bet.”

“Sorry. I’m still in, okay?” <sound of chips clinking> “So why’s A.I. not gonna get better? I keep reading how different ones passed tougher tests.”

“Well, that’s the thing. If you’re reading about it online, the bots are, too. What they read goes into their training database. Those impressive test scores may just be the result of inadvertent cheating — but the software’s so opaque that its developers simply don’t know whether or not that’s true. Just another case of the Ouroboros Effect.”

Eddie and Susan meet Cal’s bet, then Vinnie goes all‑in and shows his three queens. “Ouroboros, Sy?”

“The Norse World Snake that eats its tail. Bogus A.I.‑generated output used as A.I. input yields worse output. That’s a loss, not a gain. Unlike here where my four kings take the pot.”

“Geez, Sy, again?”

~~ Rich Olcott

The Ultimate Pinhole Camera

On By rolcottIn Astronomy: Techniques, Physics: Black Holes and Relativity, UncategorizedLeave a comment

Neither Kareem nor I are much for starting conversations. We’re more the responder type so the poker hands we dealt went pretty quickly. Cathleen had a topic, though. “Speaking of black holes and polarized radio waves, I just read a paper claiming to have developed a 3‑dimensional movie of an event wider than Mercury’s orbit, all from the flickering of a single pixel.”

Eddie bets big, for him. Ten chips. “That’s a lot to ask from just a dot. And what’s polarization got to do with it?”

Cal folds but pipes up anyway. “What was the event?”

“You know Sagittarius A*, the supermassive black hole in the middle of our galaxy?”

“Yeah, one of those orange‑ring pictures.”

“Mm‑hm. Based on radio‑wave emissions from its accretion disk. That image came from a 2‑day Event Horizon Telescope study in 2017. Well, four days after that data was taken, the Chandra satellite observatory saw an X‑ray flare from the same region. The ALMA radio telescope team immediately checked the location. ALMA has excellent signal‑to‑noise and time‑resolution capabilities but it’s only one observatory, not world‑wide like the EHT. The EHT can resolve objects a hundred thousand times closer together than ALMA’s limit. But the team did a lot with what they had.”

Vinnie tends to bet big, maybe because he’s always skeptical. Fifteen chips. “You said ‘claiming‘ like there’s doubt. People don’t trust the data?”

“In science there’s always doubt. In this case, no‑one doubts the data — ALMA’s been providing good observations for over a decade. The doubt’s in the completely new AI‑driven data reduction technique the team used. Is what they did valid? Could their results have been affected by a ‘hallucination’ bug?”

Vinnie doesn’t let go. “What did they do, what have people been doing, and what’s hallucination?”

Susan reluctantly shoves fifteen chips into the pot. “Hallucination is an AI making up stuff. I just encountered that in a paper I’m reviewing. There’s a long paragraph that starts off okay but midway it goes off on a tangent quoting numbers that aren’t in the data. I don’t believe the submitting authors even read what they sent in.”

Kareem drops out of the betting but stays in the conversation. “For a lot of science, curve‑fitting’s a standard practice. You optimize a model’s parameters against measured data. X‑ray crystallography, for example. The atoms in a good crystal are arranged in a regular lattice, right? We send a narrow beam of X‑rays at the crystal and record the intensity reflected at hundreds of angles by the atoms in different lattice planes. Inside the computer we build a parameterized model of the crystal where the parameters are the x‑, y‑ and z‑coordinates of each atom. We have computer routines that convert a given set of configuration parameters into predicted reflection intensity at each observation angle. Curve‑fitting programs cycle through the routines, adjusting parameters until the predictions match the experimental data. The final parameter values give us the atomic structure of the crystal.”

“There’s a lot of that in astrophysics and cosmology, too. This new AI technique stands that strategy on its head. The researchers started with well‑understood physics outside of the event horizon — hot rotating accretion disk, strong magnetic field mostly perpendicular to that, spacetime distortion thanks to General Relativity — and built 50,000 in‑computer examples of what that would look like from a distance.”

“Why so many?”

“The examples had to cover one or two supposed flares of different sizes and brightness at different points in their orbits, plus noise from the accretion disk’s radiation, all from a range of viewpoint angles. Mind you, each example’s only output was a single signal intensity and polarization angle (that’s two dimensions) for that specific set of disk and flare configuration parameters. The team used the example suite to train an AI specialized for assembling 2‑dimensional visual data into a 3‑dimensional model. The AI identified significant patterns in those 50,000 simulated signals. Then the team confronted the trained AI with 100 minutes of real single‑pixel data. It generated this…”

Click through to video, from Levis, et al.

“Curve‑fitting but we don’t know the curves!”

“True, Sy, but the AI does.”

“Maybe.”

~ Rich Olcott

A Non-political Polarizing Topic

On By rolcottIn Astronomy: Techniques, Physics: Black Holes and Relativity, Physics: Waves, UncategorizedLeave a comment

Vinnie gets the deck next, but first thing he does is plop a sheet of paper onto the table. “Topic is black holes, of course. Everybody’s seen this, right?”

“Sure, it’s the new view of the Milky Way’s super-massive black hole with the extra lines. So deal already.”

“Hold your horses, Cal.” <Vinnie starts dealing.> “I’m looking for explanations. Where’d those lines come from? They swirl across the accretion disk like so much rope, right? Why aren’t they just going straight in orderly‑like? The whole thing just don’t make sense to me.”

Susan bets a few chips. “I saw a similar pop‑sci article, Vinnie. It said the lines trace out polarization in the light waves the Event Horizon Telescope captured. Okay, radio waves — same thing just longer wavelength. Polarized radio waves. I’ve measured concentrations of sugar and amino acid solutions by how much the liquid rotates polarized light, but the light first went through a polarizing filter. How does a black hole make polarized waves?”

Kareem matches Susan’s bet. “Mm‑hm. We use polarized light passing through thin sections of the rocks we sample to characterize the minerals in them. But like Susan says, we don’t make polarized light, we use a filter to subtract out the polarization we don’t want. You’re the physicist, Sy, how does the black hole do the filtering?”

Plane‑polarized electromagnetic wave
 Electric (E) field is red
 Magnetic (B) field is blue
(Image by Loo Kang Wee and Fu-Kwun Hwang from Wikimedia Commons)

My hand’s good so I match the current ante. “It doesn’t. There’s no filtering, the light just comes out that way. I’d better start with the fundamentals.” <displaying Old Reliable> “Does this look familiar, Vinnie?”

“Yeah, Sy, you’ve used it a lot. That blue dot in the back’s an electron, call it Alice, bobbing straight up and down. That’s the polarization it’s puttin’ on the waves. The red lines are the force that another electron, call it Bob, feels at whatever distance away. Negative‑negative is repelling that so Bob goes down where the red line goes up but you get the basic idea.”

“The blue lines are important here.”

“I’m still hazy on those. They twist things, right?”

“That’s one way to put it. Hendrik Lorentz put it better when he wrote that Bob in this situation experiences one force with two components. There’s the red‑line charge‑dependent component, plus the blue‑line component that depends on the charge and Bob’s motion relative to Alice. If the two are moving in parallel—”

“The same frame, then. I knew frames would get into this somehow.”

“It’s hard to avoid frames when motion’s the subject. Anyway, if the two electrons are moving in parallel, the blue‑line component has zero effect. If the two are moving in different directions, the blue‑line component rotates Bob’s motion perpendicular to Alice’s red‑line polarization plane. How much rotation depends on the angle between the two headings — it’s a maximum when Bob’s moving perpendicular to Alice’s motion.”

“Wait, if this is about relative motion, then Bob thinks Alice is twisting, too. If she thinks he’s being rotated down, then he thinks she’s being rotated up, right? Action‑reaction?”

“Absolutely, Vinnie. Now let’s add Carl to the cast.”

“Carl?”

Alice and Bob’s electromagnetic interaction
begets motion that generates new polarized light.

“Distant observer at right angles to Alice’s polarization plane. From Carl’s point of view both electrons are just tracking vertically. Charges in motion generate lightwaves so Carl sees light polarized in that plane.”

Cathleen’s getting impatient, makes her bet with a rattle of chips. “What’s all this got to do with the lines in the EHT image?”

“The hole’s magnetic field herds charged particles into rotating circular columns. Faraday would say each column centers on a line of force. Alice and a lot of other charged particles race around some column. Bob and a lot of other particles vibrate along the column and emit polarized light which shows up as bright lines in the EHT image.”

“But why are the columns twisted?”

“Orbit speed in the accretion disk increases toward its center. I’d bet that’s what distorts the columns. Also, I’ve got four kings.”

“That takes this pot, Sy.”

~~ Rich Olcott

New Volcano, Old Crater

On By rolcottIn Astronomy: Planetary Science, UncategorizedLeave a comment

Now Eddie’s dealing the cards and the topic choice. “So I saw something on TV about a new volcano on Mars. You astronomy guys have been saying Mars is a dead planet, so what’s with a new volcano? Pot’s open.”

Vinnie’s got nothing, throws down his hand. So does Susan, but Kareem antes a few chips. “I doubt there’s a new volcano, it’s probably an old one that we just realized is there. We find a new old caldera on Earth almost every year. Sy, I’ll bet your tablet knows about it.”

I match Kareem’s bet and fire up Old Reliable. A quick search gets me to the news item. “You’re right, Kareem, it’s a new find of an old volcano. This article’s a puff‑piece but the subject’s in your bailiwick, Cathleen.”

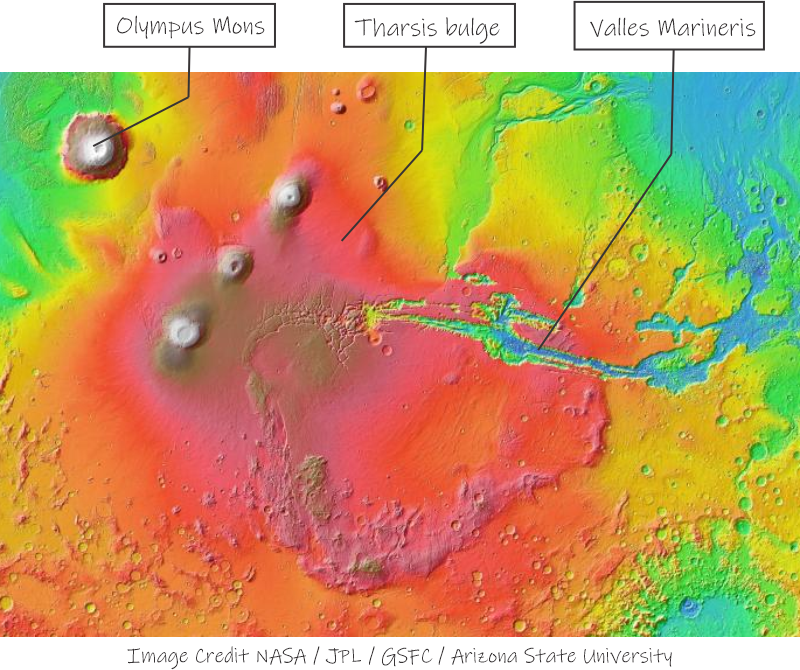
Cathleen puts in her bet and pulls out her tablet. “You’re right, Kareem. It’s a volcano we all saw but no‑one recognized until this two‑person team did. Here’s a wide‑angle view of Mars to get you oriented. North is up top, east is to the right just like usual.”

“Gaah. Looks like a wound!”

“We’ll get to that. The colors code for elevation, purple for lowlands up through the rainbow to red, brown and white. Y’all know about Olympus Mons, the 22‑kilometer tallest volcano in the Solar System, and there’s Valles Marineris, at 4000 kilometers the longest canyon. The Tharsis bulge is red‑to‑pink because it’s higher than most all the rest of the planet’s surface. Do you see the hidden volcano?”

“It’s hard to tell the volcanos from the meteor craters.”

“Understandable. Let me switch to a closer view of the canyon’s western end. This one’s in visible light, no color‑coding games. The middle one of the three Tharsis volcanos is to the left, no ginormous meteor craters in the view. Noctis labyrinthus, ‘the Labyrinth of Night.’ is that badlands region left of center. Lots of crazy canyons that go helter‑skelter.”

“That’s more Mars‑ish, but it’s still unhealthy‑looking.”

“It is a bit rumpled. Do you see the volcano?”

“Mmm, no.”

“This should help. It’s a close-up using the elevation colors to improve contrast.”

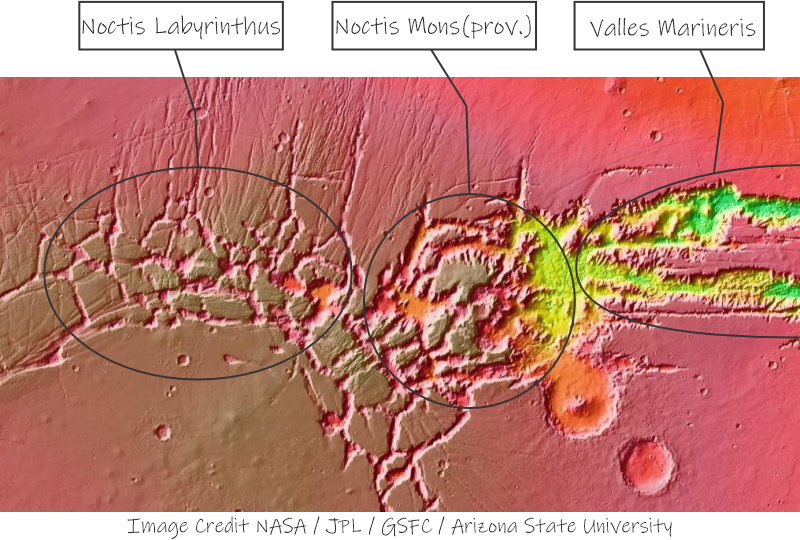
“Wow, the area inside that circle sure does look like it’s organized around its center, not higgledy-piggledy like what’s west of it. That brown image had something peaky right about there. What’s ‘prov’?”

“Good eye, Susan. The ‘prov’ means ‘provisional‘ because names aren’t real until the International Astronomical Union blesses them. The peak is nine kilometers high, almost half the height of Olympus Mons. The concentric array of canyons and mesas around it certainly make it look like a collapsed and eroded volcano. But IAU demands more evidence than just ‘look like.’ Using detailed spectroscopic data from two different Mars orbiters, the team found evidence of hydrated minerals plus structural indications that their proposed volcano either punched through a glacier or flowed onto one. Better yet, the mesas all tilt away from the peak, and the minerals are what you’d expect from water reacting with fresh lava.”

“Did they use the word ‘ultramafic‘?”

“I don’t think so, Kareem, just ‘mafic‘.”

“From underground but not deep down, then.”

“I suppose.”

Cal bets. “You said we’d get back to wounds. What was that about?”

“Well, just look at all that mess related to the Tharsis bulge — higher than all its surroundings, massive volcanos nearby, the Noctis badlands, Valles Marineris that doesn’t look water‑carved but has that delta at its eastern end. Why is all of that clustered in just one part of the planet? Marsologists have dozens of hypotheses. My own favorite centers on Hellas basin. It’s the third largest meteor strike in the Solar System and just happens to be almost exactly on the opposite side of Mars.”

Eddie looks a bit gobsmacked. “A wallop like that would carry a lot of momentum. Kareem, can a planet’s interior just pass that along in a straight line?”

“Could be, depending. If it’s solid or high‑viscosity, I guess so. If it’s low‑viscosity you’d get a doughnut‑shaped circulatory pattern inside that’d turn the energy into heat and vulcanism. How long was Mars cooling before the hit?”

“We don’t know.”

Cal’s pair of jacks apologetically takes the pot.

~~ Rich Olcott

Sounds, Harsh And Informative

On By rolcottIn Astronomy: Techniques, Chemistry, Physics: Waves, UncategorizedLeave a comment

Vinnie’s frowning. “Wait, Sy. I get how molecules bumping into each other can carry a sound wave across space if the frequency’s low enough and that can maybe account for galaxies having spiral arms. So what’s that got to do with the Sonication Project?”

Now Jeremy’s frowning. “What’s sonication got to do with Astronomy? One of my girl friends uses sonication in Biology lab when she’s studying metabolism in plant cells.”

“Whoa! Sonification, not sonication — they could have called it soundify‑cation but sonification‘s classier. ‘Sonication‘ uses high‑intensity ultrasound to jiggle a sample so roughly that cell walls can’t take the stress. They break open and spill the cell’s internal soup out where your friend’s probes can get to it. Tammy, the chemist down the hall from my lab, uses sonication, too.”

“Whoa, Susan, wouldn’t sonication break up molecules?”

“Depends on the frequency and intensity, Vinnie. Sonication can mess up big floppy proteins and DNA, but chemists who play with little peptides and such don’t care. Tammy does solid‑state chemistry. She’s looking for superconductors and she actually does want to break things. The field’s hot category these days is complex copper oxides doped with other metals. You synthesize those compositions by sintering a mix of oxide powders. To maximize contact for a good reaction you need really fine‑grained powders. Sonication does a great job of shattering brittle oxide grains down to bits just a few‑score atoms wide. But Tammy’s technique is even more elegant than that.”

“Elegant sneezes from the powder?”

Susan wallops my shoulder. “No, Sy, the powders are so small they’d be a lung hazard and some of them are toxic. Everything’s done behind respiratory protection.” <Susan doesn’t joke about lab safety.> “There’s evidence that some of these materials are only superconductive if they have the right kind of layered structure. Turns out that if Tammy has her sonicator setup just right when she preps a sample for sintering, the sound wave peaks and valleys inside the machine make the shattered particles settle out in interesting layers.”

“Like Chladni figures.”

“Oh, you know about them.”

“Yeah, I wrote about them a few years ago. Waves do surprising things.”

The Bullet Cluster (1E 0657-56)
Sonification Credit: NASA/CXC/SAO/K.Arcand,
SYSTEM Sounds (M. Russo, A. Santaguida), based on X-Ray image by NASA/CXC/CfA/M.Markevitch,
Optical and lensing map: NASA/STScI, Magellan/U.Arizona/D.Clowe,
Lensing map: ESO WFI

Vinnie’s getting impatient. “So what’s sonification then?”

Tinkly music bursts from Cathleen’s tablet. “This one’s listenable, Susan, and it’s a nice demonstration of what sonification’s about and how arbitrary it can be. You start with complicated multi‑dimensional data and use some process to turn it into audible signals. The process algorithm can use any sound characteristics you like — loudness, pitch, timbre, whatever. This example started with the famous Bullet Cluster image that most people accept as the first direct confirmation of dark matter. All the white‑ish thingies are galaxies except for the ones with pointy artifacts — those are stars. The pink haze is X‑ray light from the same region. The blue haze comes from a point‑by‑point assessment of how badly the galaxy images have been distorted by gravitational lensing — that’s an estimate of the dark matter mass between us and that region of sky. Got all that?”

“And that vertical line is like a scan going across the picture?”

“It’s not like a scan, it is a scan. Imagine a collection of tiny multi‑spectral cameras arranged along a carrier bar. As the bar travels across the picture, each camera emits three signals proportional to the amount of white, pink and blue light it sees. If you look close, just to the right of the line, you’ll see moving white, red and blue line‑charts of the respective signals.”

“That’s fine, but what’s with the sound effects?”

“The Project’s sonification processing generated hiss and rumble sounds whose loudness is proportional to the red and blue signals. Each white‑ish peak became a ping whose pitch indicates position along that bar.”

“Why go to all that trouble?”

“The sounds encode the picture for vision‑challenged people. Beyond that, the Project participants hope that with the right algorithms, their music will reveal things the pictures don’t.”

“They should avoid screamy sounds.”

~~ Rich Olcott

Galaxies Sing In A Low Register

On By rolcottIn Astronomy, Physics: Waves, UncategorizedLeave a comment

Jeremy gets a far‑away look. ”It’s gotta be freakin’ noisy inside the Sun.” just as our resident astronomer steps into Cal’s Coffee.

“Wouldn’t bet that, Jeremy. Depends on where you are in the Sun and on how you define noise.”

Vinnie booms, quietly. ”We just defined it, Cathleen. Atoms or molecules bumping each other in compression waves. Oh, wait, that’s ‘sound,’ you said ‘noise.’ Is that different?”

Susan slurps the last of her chocolate latte. ”Depends on your mood, I guess. All noise is sound, but some sound can be signal. Some people don’t like my slurping so for them it’s noise but Cal hears it as an order for another which makes him happy.”

“Comin’ up, Susan. Hey, Cathleen, maybe you can slap down Sy. He said spiral galaxies have something to do with sound which don’t make sense. Set him straight, okay?”

“Sy, have you all settled that sound isn’t limited to what humans hear?”

“Sure. Everybody’s agreed that infrasound and ultrasound are sound, and that Bishop Berkeley’s fallen tree made a sound even though nobody heard it. That’s probably what got Jeremy thinking about sound inside the Sun.” Jeremy nods.

“Then Vinnie’s definition is too limited and Sy’s statement is correct. Probably.”

That gets a reaction from everyone, though mine is a smile. ”Let ’em have it, Cathleen.”

“Okay. Let’s take Jeremy’s idea first and then we’ll get to galaxies.” <fetches her tablet from her purse and a display on her tablet> “Here’s a diagram of the Sun I did for class. If you restrict ‘sound‘ to mean only coherent waves borne by atoms and molecules, there’s no sound in the innermost three zones. The only motion, if Sy grants I can call it that, is photons and subnuclear particles randomly swapping between adjacent nuclei that are basically locked into position by the pressure. Not much actual atomic motion until you’re up in the Convection Zone where rising turbulence is the whole game. Even there most of the particles are ions and electrons rather than neutral atoms. Loud? You might say so but it’d be a continuous random crackle‑buzz, not anything your ears would recognize. Sound waves as such don’t happen until you reach the atmospheric layers. Up there, oh yes, Jeremy, it’s loud.”

Geologist Kareem is a quiet guy, normally just sits and listens to our chatter, but Cathleen’s edging onto his turf. ”How about seismic waves? If there’s a big flare or CME up top, won’t that send vibrations all the way through?”

“Good point, Kareem. Yes, the Sun has p and s waves just like Earth does, but they travel no deeper than the Convection Zone. A different variety we may not have, g waves, would involve the core. Unfortunately, theory says g waves are so weak that the Convection Zone’s chaos swamps them. Anyway, the Sun’s s, p and g waves wouldn’t contribute to what Jeremy would hear because their frequencies are measured in hours or days. Can I get to galaxies now?”

“Please do.”

A Hubble view of NGC 5457, the Pinwheel Galaxy. Credit: NASA, ESA.

“Thanks.” <another display on her tablet> “Here’s a classic spiral galaxy. Gorgeous, huh? The obvious question is, is it winding in or spraying out? The evidence says ‘No‘ to both. The stars are neither pulled into a whirlpool nor flung out from a central star‑spawner. By and large, the stars or clusters of them are in perfectly good Newtonian orbits around the galactic center of gravity. So why are they collected into those arms? Here’s a clue — most of the blue stars are in the arms.”

“What’s special about blue stars?”

“In general, blue stars are large, hot and young. Our Sun is yellow, about halfway through a 10‑million‑year lifetime. The blue guys burn through their fuel and go nova in a tenth of that time. Blue stars out there tell us that the arms serve as stellar nurseries. It’s not stars gathering into arms, it’s galaxy‑wide rotating waves of gas birthing stars there. There’s argument about whether the wave rotation is intrinsic or whether there’s feedback as each wave is pulled along by star formation at the leading edge and pushed by novae at the trailing edge. Sy’s point, though, is that an arm‑dwelling old red star would experience the spinning gas density pattern as a basso profundo sound wave with a frequency even lower than the million‑year range. Right, Sy?”

“As always, Cathleen.”

~~ Rich Olcott

  • More thanks to Alex.

A Spherical Bandstand

On By rolcottIn Astronomy: Planetary Science, Mathematics, Mathematics: Spherical Harmonics, UncategorizedLeave a comment
Radial harmonics Rn = Ln e-nr

“Whoa, Sy, something’s not right. Your zonal harmonics — I can see how latitudes go from pole to pole and that’s all there are. Your sectorial harmonic longitudes start over when they get to 360°, fine. But this chart you showed us says that the radius basically disappears crazy close to zero. The radius should keep going forever, just like x, y and z do.”

“Ah, I see the confusion, Susan. The coordinate system and the harmonic systems and the waves are three different things, um, groups of things. You can think of a coordinate system as a multilevel stage where chords of harmonic musicians can interact to play a composition of wave signals. The spherical system has latitude and longitude levels for the brass and woodwind players, plus one in back for the linear percussion section. Whichever direction the brass and woodwinds point, that’s where the signals go out, but it’s the percussion that determines how far they get. Sure, radius lines extend to infinity but except for R0 radial harmonics damp out pretty quickly.”

“Signals… Like Kaski’s team interpreted Juno‘s orbital twitches as a signal about Jupiter’s gravitational unevenness. Good thing Juno got close enough to be inside the active range for those radial harmonics. How’d they figure that?”

“They probably didn’t, Cathleen, because radial harmonics don’t fit easily into real situations. First problem is scale — what units do you measure r in? There’s an easy answer if the system you’re working with is a solid ball, not so easy if it’s blurry like a protein blob or galaxy cluster.”

“What makes a ball easy?”

“Its rigid surface that doesn’t move so it’s always a node. Useful radial harmonics must have a node there, another node at zero and an integer number of nodes between. Better yet, with the ball’s radius as a natural length unit the r coordinate runs linearly between zero at the center and 1.0 at the surface. Simplifies computation and analysis. In contrast, blurries usually don’t have convenient natural radial units so we scrabble around for derived metrics like optical depth or mixing length. If we’re forced into doing that, though, we probably have worse challenges.”

“Like what?”

“Most real-world spherical systems aren’t the same all the way through. Jupiter, for instance, has separate layers of stratosphere, troposphere, several chemically distinct cloud‑phases, down to helium raining on layers of hydrogen in liquid, maybe slushy or even solid form. Each layer has its own suite of physical properties that put kinks into a radial harmonic’s smooth curve. Same problem with the Sun.”

“How about my atoms? The whole Periodic Table is based on atoms having a shell structure. What about the energy level diagrams for atomic spectra? They show shells.”

“Well, they do and they don’t, Susan. Around the turn of the last Century, Lyman, Balmer, Paschen, Brackett and Pfund—”

“Sounds like a law firm.”

“<ironically> Ha, ha. No, they were experimental physicists who gave the theoreticians an important puzzle. Over a 40‑year period first Balmer and then the others, one series at a time, measured the wavelengths of dozens of lines in hydrogen’s spectrum. ’Okay, smarties, explain those!‘ So the theoreticians invented quantum mechanics. The first shot did a pretty good job for hydrogen. It explained the lines as transitions between discrete states with different energy levels. It then explained the energy levels in terms of charge being concentrated at different distances from the nucleus. That’s where the shell idea came from. Unfortunately, the theory ran into problems for atoms with more than one electron.”

“Give us a second… Ah, I get why. If one electron avoids a node, another one dives in there and that radius isn’t a node any more.”

“Got it in one, Cathleen. Although I prefer to think of electrons as charge clouds rather than particles. Anyhow, when an atom has multiple charge concentrations their behavior is correlated. That opens the door to a flood of transitions between states that simply aren’t options for a single‑electron system. That’s why the visible spectrum of helium, with just one additional electron, has three times more lines than hydrogen does.”

“So do we walk away from spherical harmonics for atoms?”

“Oh, no, Susan, your familiar latitude and longitude harmonics fit well into the quantum framework. These days, though, we mostly use combinations of radial fade‑aways like my Sn00 example.”

~~ Rich Olcott