Tag: Inertial frame

Constant’s Companion

On By rolcottIn CosmologyLeave a comment

“It’s like Mark Twain said, Jeremy — ‘History may not repeat itself, but it rhymes.‘ Newton identified gravity as a force; Einstein proposed the Cosmological Constant. Newton worked the data to develop his Law of Gravity; Friedmann worked Einstein’s theory to devise his model of an exponentially expanding Universe. Newton was uncomfortable with gravity’s ability to act at a distance; Einstein called the Cosmological Constant ‘his greatest blunder.’ The parallels go on.”

“Why didn’t Einstein like the Constant if it explains how the Universe is expanding?”

“It wasn’t supposed to. Expanding Universes weren’t in fashion a century ago when Einstein wrote that paper. At the time everyone including Einstein thought we live in a steady state universe. His first cut at a General Relativity field equation implied a contracting universe so he added a constant term to balance out the contraction even though it made the dynamics look unstable — the Constant had to have just the right value for stability. A decade later Hubble’s data pointed to expansion and Friedman’s equations showed how that can happen.”

“I guess Einstein was embarrassed about that, huh, Mr Moire?”

“Well, he’d thought all along that the Constant was mathematically inelegant. Besides, the Constant isn’t just a number or a term in an equation, it’s supposed to represent a real process in operation. Like Newton’s problem with gravity, Einstein couldn’t identify a mechanism to power the Constant.”

“Power it to do what?”

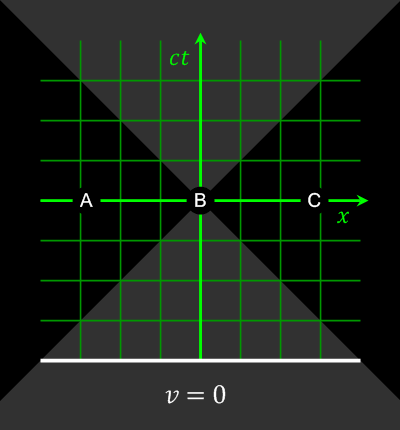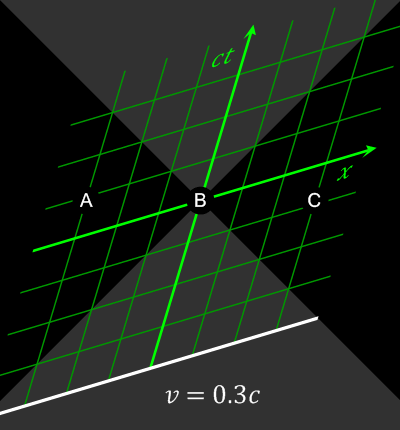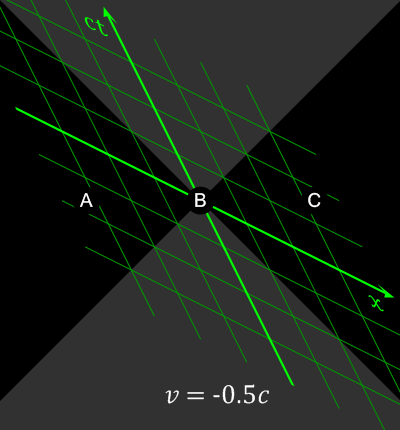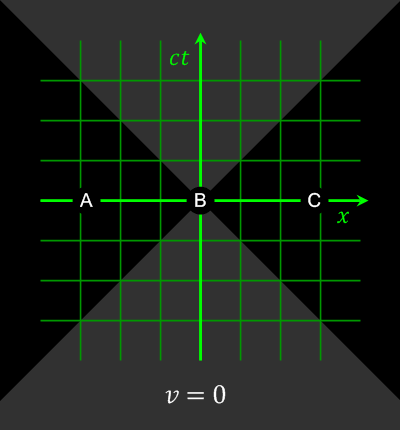
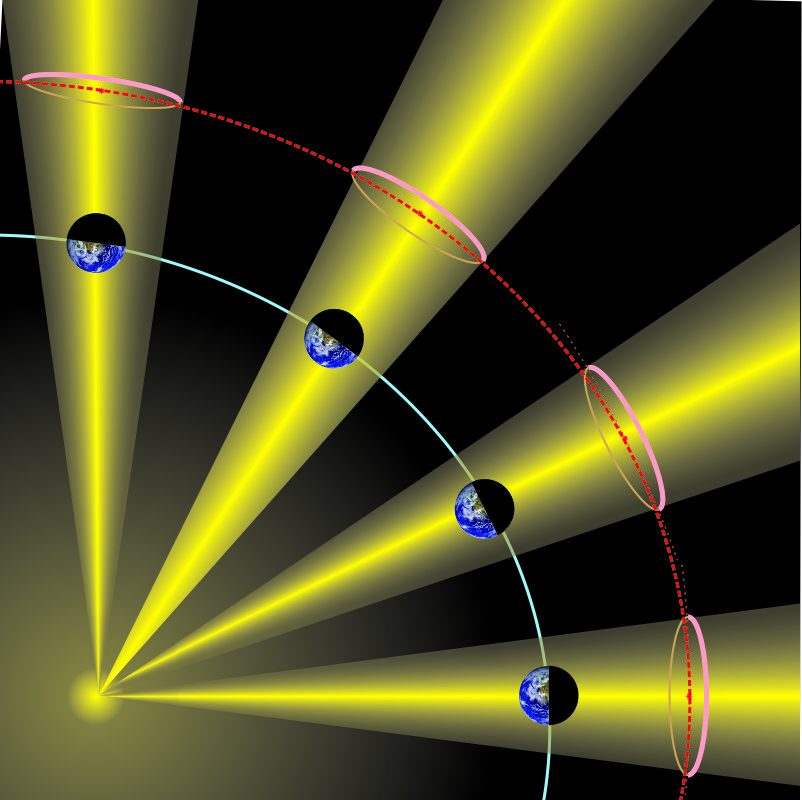
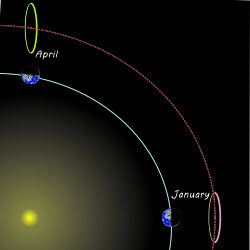
“Think about universal constants, like the speed of light or the electron charge. Doesn’t matter where you are or how fast you’re traveling in which inertial frame, they’ve got the same values. If the Constant is indeed a constant, it contributes equally to cosmological dynamics from every position in space, whether inside a star or millions of lightyears from any galaxy. Every point must exert the same outward force in every direction or there’d be swirling. And it multiplies — every instant of general expansion makes new points in between the old points and they’ll exert the same force, too.”

“That’s what makes it exponential, right?”

“Good insight. It’s a pretty weak force per unit volume, weaker than gravity. We know that because galaxies and galaxy cluster structures maintain integrity even as they’re drifting apart from each other. Even so, a smidgeon of force from each unit volume in space adds up to a lot of force. Multiply force by distance traveled — that’s a huge amount of energy spent against gravity. The big puzzle is, what’s the energy source? Most of the astrophysics community nominates dark energy to power the Cosmological Constant but that’s not much help.”

“As Dr Prather says in class, Mr Moire, ‘You sound tentative. Please expound.‘ Why wouldn’t dark energy be the power source?”

“In Physics we use the word ‘energy‘ with a very specific meaning. Yes, it gets heavy use with sloppy meanings in everything from show business to crystal therapy, but in hard science nearly every serious research program since the 18th Century has entailed quantitative energy accounting. The First Law of Thermodynamics is conservation of energy. Whenever we see something heating up, a chemical reaction running or a force being applied along a distance, physicists automatically think about the energy being expended and where that energy is coming from. Energy’s got to balance out. But the Constant breaks that rule — we have no idea what process provides that energy. Calling the source ‘dark energy‘ just gives it a name without explaining it.”

“Isn’t the missing energy source evidence against Friedmann’s and Einstein’s equations?”

“That’s a tempting option and initially a lot of researchers took it. Unfortunately, it seems that dark energy is a thing. Or maybe a lot of little things. Several different lines of evidence say that the Constant constitutes twice as much mass‑energy as all normal and dark matter combined. Worse yet, as the Universe expands that share will increase.”

“Wait, will the dark energy invade normal matter and break us up?”

“People argue about that. Normal matter’s held together by electromagnetic forces which are 1038 times stronger than gravity, far stronger yet than dark energy. Dark matter’s gravity helps to hold galaxies together, but who knows what holds dark matter together?”

~~ ROlcott

Time Is Where You Find It

On By rolcottIn Cosmology, Physics: Light and Relativity, UncategorizedLeave a comment

A familiar footstep in the hall outside my office, “C’mon in, Vinnie, the door’s open.”

“Got a few minutes, Sy?”

More than just “a minute.” This sounds serious so I push my keyboard aside. “Sure, what’s up?”

“I’ve been thinking about different things, putting ’em together different ways. I came up with something, sorta, that I wanted to run past you before I brought it to one of Cathleen’s ‘Crazy Theories‘ parties.”

“Why, Vinnie, you’re being downright diffident. Spill it.”

“Well, it’s all fuzzy. First part goes way back to years ago when you wrote that there’s zero time between when a photon gets created and when it gets used up. But that means that create and use-up are simultaneous and that goes against Einstein’s ‘No simultaneity‘ thing which I wonder if you couldn’t get around it using time tick signals to sync up two space clocks.”

“That’s quite a mix and I see why you say it’s fuzzy. Would you be surprised if I used the word ‘frame‘ while clarifying it?”

“I’ve known you long enough it wouldn’t surprise me. Go ahead.”

“Let’s start with the synchronization idea. You’re not the first to come up with that suggestion. It can work, but only if the two clocks are flying in formation, exactly parallel course and speed.”

“Hah, that goes back to our first talk with the frame thing. You’re saying the clocks have to share the same frame like me and that other pilot.”

“Exactly. If the ships are zooming along in different inertial frames, each will measure time dilation in the other. How much depends on their relative velocities.”

“Wait, that was another conversation. We were pretending we’re in two spaceships like we’re talking about here and your clock ran slower than mine and my clock ran slower than yours which is weird. You explained it with equations but I’ve never been good with equations. You got a diagram?”

“Better than that, I’ve got a video. It flips back and forth between inertial frames for Enterprise and Voyager. We’ll pretend that they sync their clocks at the point where their tracks cross. I drew the Enterprise timeline vertical because Enterprise doesn’t move in space relative to Enterprise. The white dots are the pings it sends out every second. Meanwhile, Voyager is on a different course with its own timeline so its inertial frame is rotated relative to Enterprise‘s. The gray dots on Voyager‘s track show when that ship receives the Enterprise pings. On the Voyager timeline the pings arrive farther apart than they are on the Enterprise timeline so Voyager perceives that Enterprise is falling farther and farther behind.”

“Gimme a sec … so Voyager says Enterprise‘s timer is going slow, huh?”

“That’s it exactly. Now look at the rotated frame. The pink dots show when Voyager sends out its pings. The gray dots on Enterprise‘s track show when the pings arrive.”

“And Enterprise thinks that Voyager‘s clock is slow, just backwards of the other crew. OK, I see you can’t use sync pulses to match up clocks, but it’s still weird.”

“Which is where Lorentz and Minkowski and Einstein come into the picture. Their basic position was that physical events are real and there should be a way to measure them that doesn’t depend on an observer’s frame of reference. Minkowski’s ‘interval‘ metric qualifies. After converting time and location measurements to intervals, both crews would measure identical spacetime separations. Unfortunately, that wouldn’t help with clock synchronization because spacetime mixes time with space.”

“How about the photons?”

“Ah, that’s a misquotation. I didn’t say the time is zero, I said ‘proper time‘ and that’s different. An object’s proper time is measured by its clock in its inertial frame while traveling time t and distance d between two events. Anyone could measure t and d in their inertial frame. Minkowski’s interval is defined as s=√[(ct)²‑d²]. Proper time is s/c. Intuitively I think of s/c as light’s travel time after it’s done traversing distance d. In space, photons always travel at lightspeed so their interval and proper time are always zero.”

“Photon create and use-up aren’t simultaneous then.”

“Only to photons.”

~~ Rich Olcott

Now And Then And There

On By rolcottIn Cosmology, James Webb Space Telescope, Physics: Light and Relativity, UncategorizedLeave a comment

Still at our table in Al’s otherwise empty coffee shop. We’re leading up to how Physics scrambled ‘Now‘ when a bell dings behind the counter. Al dashes over there. Meanwhile, Cathleen scribbles on a paper napkin with her colored pencils. She adds two red lines just as Al comes back with a plate of scones. “Here, Sy, if you’re going to talk Minkowski space this might be useful.”

“Hah, you’re right, Cathleen, this is perfect. Thanks, Al, I’ll have a strawberry one. Mmm, I love ’em fresh like this. OK, guys, take a look at Cathleen’s graphy artwork.”

“So? It’s the tile floor here.”

“Not even close, Mr Feder. Check the labels. The up‑and‑down label is ‘Time’ with later as higher. The diagram covers the period we’ve been sitting here. ‘Now‘ moves up, ‘Here’ goes side‑to‑side. ‘Table‘ and ‘Oven‘, different points in space, are two parallel lines. They’re lines because they both exist during this time period. They’re vertical because neither one moves from its relative spatial position. Okay?”

“Go on, Moire.”
  ”Makes sense to me, Sy.”

“Good. ‘Bell‘ marks an event, a specific point in spacetime. In this case it’s the moment when we here at the table heard the bell. I said ‘spacetime‘ because we’re treating space and time as a combined thing. Okay?”

“Go on, Moire.”
  ”Makes sense to me, Sy.”

“So then Al went to the oven and came back to the table. He traveled a distance, took some time to do that. Distance divided by time equals velocity. ‘Table‘ has zero velocity and its line is vertical. Al’s line would tilt down more if he went faster, okay?”

“Mmmm, got it, Sy.”
  ”Cute how you draw the come-back label backwards, lady. Go on, Moire.”

“I do my best, Mr Feder.”

“Fine, you’ve got the basic ideas. Now imagine all around us there’s graph paper like this — except there’s no paper and it’s a 4‑dimensional grid to account for motion in three spatial dimensions while time proceeds. Al left and returned to the same space point so his spacetime interval is just the time difference. If two events differ in time AND place there’s special arithmetic for calculating the interval.”

“So where’s that get us, Moire?”

“It got 18th and 19th Century Physics very far, indeed. Newton and everyone after him made great progress using math based on a nice stable rectangular space grid crossed with an orderly time line. Then Lorentz and Poincaré and Einstein came along.”

“Who’s Poincaré?”

“The foremost mathematician of nineteenth Century France. A mine safety engineer most days and a wide‑ranging thinker the rest of the time — did bleeding‑edge work in many branches of physics and math, even invented a few branches of his own. He put Lorentz’s relativity work on a firm mathematical footing, set the spacetime and gravity stage for Minkowsky and Einstein. All that and a long list of academic and governmental appointments but somehow he found the time to have four kids.”

Simultaneity Animation by “Acdx”
licensed under Creative Commons Attribution-Share Alike 4.0 International.

“A ball of fire, huh? So what’d he do to Newton’s jungle gym?”

“Turned its steel rod framework into jello. Remember how Cathleen’s Minkowski diagram connected slope with velocity? Einstein showed how Lorentz’s relativity factor sets a speed limit for our Universe. On the diagram, that’d be a minimum slope. Going vertical is okay, that’s standing still in space. Going horizontal isn’t, because that’d be instantaneous travel. This animation tells the ‘Now‘ story better than words can.”

“Whah?”
  ”Whah?”

“We’re looking down on three space travelers and three events. Speeds below lightspeed are within the gray hourglass shape. The white line perpendicular to each traveler’s time line is their personal ‘Now‘. The travelers go at different velocities relative to us so their slopes and ‘Now‘ lines are different. From our point of view, time goes straight up. One traveler is sitting still relative to us so its timeline is marked ‘v=0‘ and parallels ours. We and the v=0 traveler see events A, B and C happening simultaneously. The other travelers don’t agree. ‘Simultaneous‘ is an illusion.”

~~ Rich Olcott

Hyperbolic plane image by Murdock Grewar,
licensed under Creative Commons Attribution-Share Alike 4.0 International.

E Pluribus

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Space Travel, UncategorizedLeave a comment

Mr Feder’s a determined fault‑finder. “That gold on James Webb Space Telescope‘s mirror — it’s gonna make all its pictures look funny, yellow‑like instead of whatever the real colors are.”

Cathleen bristles a little. “We astronomers have built our science on recognizing. accounting for and overcoming instrument limitations. Hubble, for instance, went up with a mirror that had been misground so its resolution was a factor of 10 worse than it was supposed to be. It took three years for NASA to install corrective optics. In the meantime we devised a whole catalog of math and computer techniques for pulling usable data out of the mess. Anyway, JWST‘s not designed to make pretty pictures.”

“I thought it was gonna replace Hubble. If it can’t take pictures, what’re we putting it up there for?”

“It’s a successor, not a replacement. JWST is designed to answer a completely different set of questions from the ones that Hubble has been used for. I’m sure we’ll keep using Hubble for as long as it continues to operate. By the way, the Hubble pictures you’ve seen aren’t what Hubble took.”

“Bunk! I’ve seen Hubble shots of the Moon and they look just like what I see through my binocs. Same colors and everything.”

“Not much color in the Moon, Mr Feder. Just different grays except for during a lunar eclipse.”

“That’s true, Al, but the resemblance is no accident. All major telescopes including Hubble, gray‑scale is all they do. Professional and amateur scientists help out by combining and coloring those gray‑scale images.”

“Wait, how do they combine images? Back in the film days I’d forget to wind forward after taking a picture and the double exposures were always a mess.”

“Film and digital are very different technologies, Mr Feder. The sensors in your camera’s film were microscopic silver halide crystals embedded in the coating. Each photon that reached a crystal transformed one silver ion to elemental silver and darkened the image there just a bit. More photons in a particular area, more darkening. There’s no reset, so when you clicked twice on a frame the new darkening supplemented what was already there. Those silver atoms and their location on the film encoded the photos you took.”

<with a sneer> “Wooo — encoded! What’d the processing labs do, count the atoms?”

“In an analog sort of way. Your lab made positive prints by shining light through your negatives onto photosensitive paper that worked the same way as the film. Shadow from the negative’s dark silver atoms prevented silver ion darkening in the corresponding part of the paper. What was bright in the original scene came out bright in the print. And vice‑versa.”

“But I was taking color photos.”

“Same analog scheme but with fancier chemistry. Your color film had three photosensitive layers. Each layer was designed to record a different set of wavelengths, red, green or blue. Blue photons would darken the blue‑sensitive layer and so on. From then on the encoding and decoding logic worked the same, color by separate color. Your eyes combine the colors. JWST‘s cameras don’t do any of that.”

“I guess not, it being a million miles away from processing labs.”

“Right, we can only work with numbers that can be transmitted back to Earth. Modern telescopes use digital sensors, dense grids of transistor‑size devices that literally count the photons that strike them. Graph how many photons hit each part of the grid during an interval and you’ve got a picture. Better yet, you can do arithmetic on the counts. That opens up a world of analytical and pictorial opportunities that were tedious or impossible with photographic data.” <opens laptop, taps keys> “Here’s a lovely example I recently received from NASA’s Astronomy Picture of the Day service. Gorgeous, hm?”

“Symbiotic R Aquarii” — Image Credit: Optical (red, blue): NASA/ESA/STScI;
X-ray (purple): NASA/CXC/SAO/R. Montez et al.;
Processing: Judy Schmidt (CC BY-NC-SA)

“Wow.”
 ”Wow.”
  ”Wow.”

“Image arithmetic in action. That’s two stars in weird orbits around each other. Ms Schmidt combined two Hubble images with one from Chandra, a separate telescope looking at a different part of the spectrum. Old‑style astrophotography couldn’t do that.”

~~ Rich Olcott

Which Way Is Up?

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

“OK, Moire, the Attitude Control System’s reaction wheels swing James Webb Space Telescope through whatever angle changes it wants, but how does ACS know what direction JWST‘s at to begin with? Does it go searching through that million‑star catalog to find something that matches?”

“Hardly, Mr Feder, that’d be way too much work for a shipboard computer. No, ACS consults the orientations maintained by a set of gyroscopes that are mounted on JWST‘s framework. Each one points along an unvarying bearing relative to the Universe, no matter how the satellite’s situated.”

“Gyroscopes? Like the one I had as a kid? Winding the string around the axle was a pain and then however hard I pulled the string I couldn’t keep one going for more than half a minute. It always wobbled anyway. Bad choice.”

“Not the JWST choice, NASA mostly doesn’t do toys. Actually, the gyroscope you remember has a long and honorable history. Gimbals have been known and used in one form or another for centuries. A few researchers mounted a rotor inside a gimbal set for various purposes in the mid‑1800s, but it was Léon Foucault who named his gadget a gyroscope when he used one for a public demonstration of the Earth’s rotation. People used to go to lectures like we go to a show. Science was popular in those days.”

“Wait — Foucault? The pendulum guy?”
 ”Wait — Foucault? The knife‑edge test guy?”

“Our science museum used to have a big pendulum. I loved to watch it knock down those domino thingies one by one as it turned around its circle. Then they took it out to make room for another dinosaur or something.”

“Yup. A museum’s most precious resource is floorspace. That weight swinging on a long wire takes up a lot of square feet. Foucault’s pendulum was another of his Earth‑rotation demonstrations, just a year after the gyroscope show. Yeah, Al, same guy — Foucault invented that technique you use to check your telescope mirrors. He pioneered a lot of Physics. He showed that the absorption spectrum of a gas when a light shines through it matches the spectrum it emits when you heat it up. His lightspeed measurement came within one percent of our currently accepted value. ”

Astronomer Cathleen shakes her head. “Imagine, 200 years after Kepler and Newton, yet people in Foucault’s day still needed convincing that the Earth is a globe floating in space. A century and a half later some still do. <sigh> Funny, isn’t it, how Foucault was working at the same time on two such different phenomena.”

“Not so different, Cathleen. Both demonstrate the same underlying principle — inertia relates to the Universe and doesn’t care about local conditions. Foucault was really working on inertia. He made use of two different inertial effects for his demonstrations. By the way, Mr Feder, the pendulum doesn’t turn. The Earth turns beneath the pendulum to bring those domino thingies into target position.”

“That’s hard to believe.”

“Could be why his demonstrations used two different phenomena. Given 19th Century technology, those were probably his best options.”

“If only he’d had lasers, huh?”

“One kind of modern gyroscope is laser‑based. Uses photons going around a ring. Actually, photons or pulses of them going around the same ring in opposite directions. When the ring itself rotates, the photons or pulses going against the rotation encounter the Start point sooner than their opposites do. Time the difference and you can figure the rotation rate. Unfortunately, Foucault didn’t have lasers or the exquisite timing devices we have today. But that’s not the kind of gyroscope JWST carries, anyway.”

“OK, I’ll bite. What does it use?”

“The slickest one yet, Al. If you carefully tap the rim of a good wine glass it’ll vibrate like the red line here. The dotted blue circle’s the glass at rest. Under the right conditions inertia holds the planes of vibration steady even if the glass itself rotates. People have figured out how to use that principle to build extremely accurate. reliable and low‑maintenance gyroscopes for measuring and stabilizing rotations. JWST carries a set.”

“Nothing to lubricate, eh?”

Portrait of Léon Foucault from Wikimedia under Creative Commons Attribution 3.0 Unported license.

~~ Rich Olcott

Turn This Way to Turn That Way

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Newton and Gravity, Space Travel, UncategorizedLeave a comment

“I don’t understand, Sy. I get that James Webb Space Telescope uses its reaction wheels like a ship uses a rudder to change direction by pushing against something outside. Except the rudder pushes against water but the reaction wheels push against … what, the Universe?”

“Maybe probably, Al. We simply don’t know how inertia works. Newton just took inertia as a given. His Laws of Motion say that things remain at rest or persist in linear motion unless acted upon by some force. He didn’t say why. Einstein’s General Relativity starts from his Equivalence Principle — gravitational inertia is identical to mechanical inertia. That’s held up to painstaking experimental tests, but why it works is still an open question. Einstein liked Mach’s explanation, that we experience these inertias because matter interacts somehow with the rest of the Universe. He didn’t speculate how that interaction works because he didn’t like Action At A Distance. The quantum field theory people say that everything’s part of the universal field structure, which sounds cool but doesn’t help much. String theory … ’nuff said.”

“Hey, Moire, what’s all that got to do with the reaction wheel thing? JWST can push against one all it wants but it won’t go anywhere ’cause the wheel’s inside it. What’s magic about the wheels?”

“JWST doesn’t want to go anywhere else, Mr Feder. We’re happy with it being in its proper orbit, but it needs to be able to point to different angles. Reaction wheels and gyroscopes are all about angular momentum, not about the linear kind that’s involved with moving from place to place.”

“HAH! JWST is moving place to place, in that orbit! Ain’t it got linear momentum then?”

Newton’s Principia, Proposition II, Theorem II

“In a limited way, pun intended. Angular momentum is linear momentum plus a radial constraint. This goes back to Newton and his Principia book. I’ve got a copy of his basic arc‑splitting diagram here in Old Reliable. The ABCDEF line is a section of some curve around point S. He treated it as a succession of short line segments ABc, BCd, CDe and so on. If JWST is at point B, for instance, Newton would say that it’s traveling with a certain linear momentum along the BCd line. However, it’s constrained to move along the arc so it winds up at D instead d. To account for the constraint Newton invented centripetal force to pull along the Sd line. He then mentally made the steps smaller and smaller until the sequence of short lines matched the curve. At the limit, a sequence of little bits of linear momentum becomes angular momentum. By the way, this step‑reduction process is at the heart of calculus. Anyway, JWST uses its reaction wheels to swing itself around, not to propel itself.”

“And we’re back to my original question, Sy. What makes that swinging happen?”

“Oh, you mean the mechanical reality. Easy, Al. Like I said, three pairs of motorized wheels are mounted on JWST‘s frame near the center of mass. Their axles are at mutual right angles. Change a wheel’s angular momentum, you get an equal opposing change to the satellite’s. Suppose the Attitude Control System wants the satellite to swing to starboard. That’d be clockwise viewed from the cold side. ACS must tell a port/starboard motor to spin its wheel faster counterclockwise. If it’s already spinning clockwise, the command would be to put on the brakes, right? Either way, JWST swings clockwise. With the forward/aft motors and the hot‑side/cold‑side motors, the ACS is equipped to get to any orientation. See how that works?”

“Hang on.” <handwaving ensues> “Yeah, I guess so.”

“Hey, Moire. What if the wheel’s already spinning at top speed in the direction the ACS wants more of?”

“Ah, that calls for a momentum dump. JWST‘s equipped with eight small rocket engines called thrusters. They convert angular momentum back to linear momentum in rocket exhaust. Suppose we need a further turn to starboard but a port/starboard wheel is nearing threshold spin rate. ACS puts the brakes on that wheel, which by itself would turn the satellite to port. However, ACS simultaneously activates selected thrusters to oppose the portward slew. Cute, huh?”

~~ Rich Olcott

Attitude Adjustment

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Space Travel, UncategorizedLeave a comment

Mr Feder has a snarky grin on his face and a far‑away look in his eye. “Got another one. James Webb Space Telescope flies in this big circle crosswise to the Sun‑Earth line, right? But the Earth doesn’t stand still, it goes around the Sun, right? The circle keeps JWST the same distance from the Sun in maybe January, but it’ll fly towards the Sun three months later and get flung out of position.” <grabs a paper napkin> “Lemme show you. Like this and … like this.”

“Sorry, Mr Feder, that’s not how either JWST or L2 works. The satellite’s on a 6-month orbit around L2 — spiraling, not flinging. Your thinking would be correct for a solid gyroscope but it doesn’t apply to how JWST keeps station around L2. Show him, Sy.”

“Gimme a sec with Old Reliable, Cathleen.” <tapping> “OK, here’s an animation over a few months. What happens to JWST goes back to why L2 is a special point. The five Lagrange points are all about balance. Near L2 JWST will feel gravitational pulls towards the Sun and the Earth, but their combined attraction is opposed by the centrifugal force acting to move the satellite further out. L2 is where the three balance out radially. But JWST and anything else near the extended Sun‑Earth line are affected by an additional blended force pointing toward the line itself. If you’re close to it, sideways gravitational forces from the Sun and the Earth combine to attract you back towards the line where the sideways forces balance out. Doesn’t matter whether you’re north or south, spinward or widdershins, you’ll be drawn back to the line.”

Al’s on refill patrol, eavesdropping a little of course. He gets to our table, puts down the coffee pot and pulls up a chair. “You’re talking about the JWST. Can someone answer a question for me?”

“We can try.”
 ”What’s the question?”
  Mr Feder, not being the guy asking the question, pooches out his lower lip.

“OK, how do they get it to point in the right direction and stay there? My little backyard telescope gives me fits just centering on some star. That’s while the tripod’s standing on good, solid Earth. JWST‘s out there standing on nothing.”

“JWST‘s Attitude Control System has a whole set of functions to do that. It monitors JWST‘s current orientation. It accepts targeting orders for where to point the scope. It computes scope and satellite rotations to get from here to there. Then it revises as necessary in case the first‑draft rotations would swing JWST‘s cold side into the sunlight. It picks a convenient guide star from its million‑star catalog. Finally, ACS commands its attitude control motors to swing everything into the new position. Every few milliseconds it checks the guide star’s image in a separate sensor and issues tweak commands to keep the scope in proper orientation.”

“I get the sequence, Sy, but it doesn’t answer the how. They can’t use rockets for all that maneuvering or they’d run out of fuel real fast.”

“Not to mention cluttering up the view field with exhaust gases.”

“Good point, Cathleen. You’re right, Al, they don’t use rockets, they use reaction wheels, mostly.”

“Uh-oh, didn’t broken reaction wheels kill Kepler and a few other missions?”

“That sounds familiar, Mr Feder. What’s a reaction wheel, Sy, and don’t they put JWST in jeopardy?”

 Gyroscope, image by Lucas Vieira

“A reaction wheel is a massive doughnut that can spin at high speed, like a classical gyroscope but not on gimbals.”

“Hey, Moire, what’s a gimbal?”

“It’s a rotating frame with two pivots for something else that rotates. Two or three gimbals at mutual right angles let what’s inside orient independent of what’s outside. The difference between a classical gyroscope and a reaction wheel is that the gyroscope’s pivots rotate freely but the reaction wheel’s axis is fixed to a structure. Operationally, the difference is that you use a gyroscope’s angular inertia to detect change of orientation but you push against a reaction wheel’s angular inertia to create a change of orientation.”

“What about the jeopardy?”

“Kepler‘s failing wheels used metal bearings. JWST‘s are hardened ceramic.”

<whew>

~~ Rich Olcott

Hyperbolas But Not Hyperbole

On By rolcottIn Astronomy: Techniques, Physics: Light and Relativity, Uncategorized2 Comments

“Minus? Where did that come from?”

<Gentle reader — If that question looks unfamiliar, please read the preceding post before this one.>

Jim’s still at the Open Mic. “A clever application of hyperbolic geometry.” Now several of Jeremy’s groupies are looking upset. “OK, I’ll step back a bit. Jeremy, suppose your telescope captures a side view of a 1000‑meter spaceship but it’s moving at 99% of lightspeed relative to you. The Lorentz factor for that velocity is 7.09. What will its length look like to you?”

“Lorentz contracts lengths so the ship’s kilometer appears to be shorter by that 7.09 factor so from here it’d look about … 140 meters long.”

“Nice, How about the clocks on that spaceship?”

“I’d see their seconds appear to lengthen by that same 7.09 factor.”

“So if I multiplied the space contraction by the time dilation to get a spacetime hypervolume—”

“You’d get what you would have gotten with the spaceship standing still. The contraction and dilation factors cancel out.”

“How about if the spaceship went even faster, say 99.999% of lightspeed?”

“The Lorentz factor gets bigger but the arithmetic for contraction and dilation still cancels. The hypervolume you defined is always gonna be just the product of the ship’s rest length and rest clock rate.”

His groupies go “Oooo.”

One of the groupies pipes up. “Wait, the product of x and y is a constant — that’s a hyperbola!”

“Bingo. Do you remember any other equations associated with hyperbolas?”

“Umm… Yes, x2–y2 equals a constant. That’s the same shape as the other one, of course, just rotated down so it cuts the x-axis vertically.”

Jeremy goes “Oooo.”

Jim draws hyperbolas and a circle on the whiteboard. That sets thoughts popping out all through the crowd. Maybe‑an‑Art‑major blurts into the general rumble. “Oh, ‘plus‘ locks x and y inside the constant so you get a circle boundary, but ‘minus‘ lets x get as big as it wants so long as y lags behind!”

Another conversation – “Wait, can xy=constant and x2–y2=constant both be right?”
  ”Sure, they’re different constants. Both equations are true where the red and blue lines cross.”

A physics student gets quizzical. “Jim, was this Minkowski’s idea, or Einstein’s?”

“That’s a darned good question, Paul. Minkowski was sole author of the paper that introduced spacetime and defined the interval, but he published it a year after Einstein’s 1905 Special Relativity paper highlighted the Lorentz transformations. I haven’t researched the history, but my money would be on Einstein intuitively connecting constant hypervolumes to hyperbolic geometry. He’d probably check his ideas with his mentor Minkowski, who was on the same trail but graciously framed his detailed write‑up to be in support of Einstein’s work.”

One of the astronomy students sniffs. “Wait, different observers see the same s2=(ct)2–d2 interval between two events? I suppose there’s algebra to prove that.”

“There is.”

“That’s all very nice in a geometric sort of way, but what does s2 mean and why should we care whether or not it’s constant?”

“Fair questions, Vera. Mmm … you probably care that intervals set limits on what astronomers see. Here’s a Minkowski map of the Universe. We’re in the center because naturally. Time runs upwards, space runs outwards and if you can imagine that as a hypersphere, go for it. Light can’t get to us from the gray areas. The red lines, they’re really a hypercone, mark where s2=0.”

From the back of the room — “A zero interval?”

“Sure. A zero interval means that the distance between two events exactly equals lightspeed times light’s travel time between those events. Which means if you’re surfing a lightwave between two events, you’re on an interval with zero measure. Let’s label Vera’s telescope session tonight as event A and her target event is B. If the A–B interval’s ct difference is greater then its d difference then she can see B — if the event is in our past but not beyond the Cosmic Microwave Background. But if a Dominion fleet battle is approaching us through subspace from that black dot, we’ll have no possible warning before they’re on us.”

Everyone goes “Oooo.”

~~ Rich Olcott

Thinking in Spacetime

On By rolcottIn Cosmology, Mathematics: Dimensions, UncategorizedLeave a comment

The Open Mic session in Al’s coffee shop is still going string. The crowd’s still muttering after Jeremy stuck a pin in Big Mike’s “coincidence” balloon when Jim steps up. Jim’s an Astrophysics post‑doc now so we quiet down expectantly. “Nice try, Mike. Here’s another mind expander to play with. <stepping over to the whiteboard> Folks, I give you … a hypotenuse. ‘That’s just a line,’ you say. Ah, yes, but it’s part of some right triangles like … these. Say three different observers are surveying the line from different locations. Alice finds her distance to point A is 300 meters and her distance to point B is 400. Applying Pythagoras’ Theorem, she figures the A–B distance as 500 meters. We good so far?”

A couple of Jeremy’s groupies look doubtful. Maybe‑an‑Art‑Major shyly raises a hand. “The formula they taught us is a2+b2=c2. And aren’t the x and y supposed to go horizontal and vertical?”

“Whoa, nice questions and important points. In a minute I’m going to use c for the speed of light. It’s confusing to use the same letter for two different purposes. Also, we have to pay them extra for double duty. Anyhow, I’m using d for distance here instead of c, OK? To your next point — Alice, Bob and Carl each have their own horizontal and vertical orientations, but the A–B line doesn’t care who’s looking at it. One of our fundamental principles is that the laws of Physics don’t depend on the observer’s frame of reference. In this situation that means that all three observers should measure the same length. The Pythagorean formula works for all of them, so long as we’re working on a flat plane and no-one’s doing relativistic stuff, OK?”

Tentative nods from the audience.

“Right, so much for flat pictures. Let’s up our game by a dimension. Here’s that same A–B line but it’s in a 3D box. <Maybe‑an‑Art‑Major snorts at Jim’s amateur attempt at perspective.> Fortunately, the Pythagoras formula extends quite nicely to three dimensions. It was fun figuring out why.”

Jeremy yells out. “What about time? Time’s a dimension.”

“For sure, but time’s not a length. You can’t add measurements unless they all have the same units.”

“You could fix that by multiplying time by c. Kilometers per second, times seconds, is a length.” His groupies go “Oooo.”

“Thanks for the bridge to spacetime where we have four coordinates — x, y, z and ct. That makes a big difference because now A and B each have both a where and a when — traveling between them is traveling in space and time. Computationally there’s two paths to follow from here. One is to stick with Pythagoras. Think of a 4D hypercube with our A–B line running between opposite vertices. We’re used to calculating area as x×y and volume as x×y×z so no surprise, the hypercube’s hypervolume is x×y×z×(ct). The square of the A–B line’s length would be b2=(ct)2+d2. Pythagoras would be happy with all of that but Einstein wasn’t. That’s where Alice and Bob and Carl come in again.”

“What do they have to do with it?”

“Carl’s sitting steady here on good green Earth, red‑shifted Alice is flying away at high speed and blue‑shifted Bob is flashing toward us. Because of Lorentz contractions and dilations, they all measure different A–B lengths and durations. Each observer would report a different value for b2. That violates the invariance principle. We need a ruggedized metric able to stand up to that sort of punishment. Einstein’s math professor Hermann Minkowski came up with a good one. First, a little nomenclature. Minkowski was OK with using the word ‘point‘ for a location in xyz space but he used ‘event‘ when time was one of the coordinates.”

“Makes sense, I put events on my calendar.”

“Good strategy. Minkowski’s next step quantified the separation between two events by defining a new metric he called the ‘interval.’ Its formula is very similar to Pythagoras’ formula, with one small change: s2=(ct)2–d2. Alice, Bob and Carl see different distances but they all see the same interval.”

“Minus? Where did that come from?”

~~ Rich Olcott

Speed Limit

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Wait, Sy, there’s something funny about that Lorentz factor. I’m riding my satellite and you’re in your spaceship to Mars and we compare notes and get different times and lengths and masses and all so we have to use the Lorentz factor to correct numbers between us. Which velocity do we use, yours or mine?”

“Good question, Vinnie. We use the difference between our two frames. We can subtract either velocity from the other one and replace v with that number. Strictly speaking, we’d subtract velocity components perpendicular to the vector between us. If I were to try to land on your satellite I’d have to expend fuel and energy to change my frame’s velocity to yours. When we matched frames the velocity difference would be zero, the Lorentz factor would be 1.0 and I’d see your solar array as a perfect 10×10‑meter square. Our clocks would tick in sync, too.”

“OK, now there’s another thing. That Lorentz formula compares our subtracted speeds to lightspeed c. What do we subtract to get c?”

“Deep question. That’s one of Einstein’s big insights. Suppose from my Mars‑bound spaceship I send out one light pulse toward Mars and another one in the reverse direction, and you’re watching from your satellite. No matter how fast my ship is traveling, Einstein said that you’d see both pulses, forward and backward, traveling at the same speed, c.”

“Wait, shouldn’t that be that your speed gets added to one pulse and subtracted from the other one?”

“Ejected mass works that way, but light has no mass. It measures its speed relative to space itself. What you subtract from c is zero. Everywhere.”

“OK, that’s deep. <pause> But another ‘nother thing—”

“For a guy who doesn’t like equations, you’re really getting into this one.”

“Yeah, as I get up to speed it grows on me. HAW!”

“Nice one, you got me. What’s the ‘nother thing?”

“I remembered how velocity is speed and direction but we’ve been mixing them together. If my satellite’s headed east and your spaceship’s headed west, one of us is minus to the other, right? We’re gonna figure opposite v‑numbers. How’s that work out?”

“You’re right. Makes no difference to the Lorentz factor because the square of a negative difference is the same as the square of its positive twin. You bring up an important point, though — the factor applies to both of us. From my frame, your clock is running slow. From your frame, mine’s the slow one. Einstein’s logic says we’re both right.”

“So we both show the same wrong time, no problem.”

“Nope, you see my clock running slow relative to your clock. I see exactly the reverse. But it gets worse. How about getting your pizza before you order it?”

“Eddie’s good, he ain’t that good. How do you propose to make that happen?”

“Well, I don’t, but follow me here. <working numbers on Old Reliable> Suppose we’re both in spaceships. I’m loafing along at 0.75c relative to Eddie’s pizza place on Earth and your ship is doing 3c. Also, suppose that we can transmit messages and mass much faster than lightspeed.”

“Like those Star Trek transporters and subspace radios.”

“Right. OK, at noon on my personal clock you tell me you’ve ordered pizza so I get one, too. Eddie slaps both our pizzas into his transporter 10 minutes later. The math works out that according to my clock you get your pizza 8.9 minutes before you put in your order. You like that?”

“Gimme a sec … nah, I don’t think so. If I read that formula right with v1 being you and v2 being me, if you run that formula for what I’d see with my velocity on the bottom, that’s a square root of a minus which can’t be right.”

“Yup, the calculation gives an imaginary number, 4.4i minutes, whatever that means. So between us we have two results that are just nonsense — I see effect before cause and you see a ridiculous time. To avoid that sort of thing, Einstein set his speed limit for light, gravity and information.”

“I’m willing to keep under it if you are.”

“Deal.”

~~ Rich Olcott