Tag: Jeremy

Squaring The Circle

On By rolcottIn Cosmology, UncategorizedLeave a comment

Vinnie gives me the eye. “That crazy theory of yours is SO bogus, Sy, and there’s a coupla things you said we ain’t heard before.”

“What’s wrong with my Mach’s Principle of Time?”

“If the rest of the Universe is squirting one thing forward along Time, then everything’s squirting everything forward. No push‑back in the other direction. You might as well say that everything’s running away from the Big Bang.”

“That’s probably a better explanation. What are the couple of things?”

“One of them was, ‘geodesic,‘ as in ‘motion along a geodesic.‘ What’s a geodesic?”

“The shortest path between two points.”

“That’s a straight line, Mr Moire. First day in Geometry class.”

“True in Euclid’s era, Jeremy, but things have moved on since then. These days the phrase ‘shortest path’ defines ‘straight line’ rather than the other way around. Furthermore, the choice depends on how you define ‘shortest’. In Minkowski’s spacetime, for instance, do you mean ‘least distance’ or ‘least interval’?”

“How are those different?”

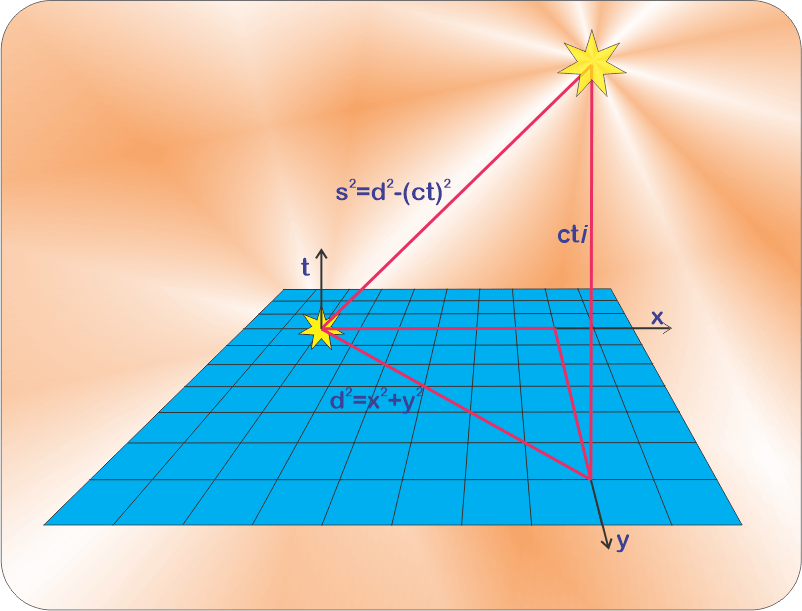
“The word ‘distance’ is a space‑only measurement. Minkowski plotted space in x,y,z terms just like Newton would have if he could’ve brought himself to use René Descartes’ cartesian coordinates. You know Euclid’s a²+b²=c² so you should have no problem calculating 3D distance as d=√(x²+y²+z²).”

“That makes sense. So what’s ‘interval’ about then?”

“Time has entered the picture. In Minkowski’s framework you handle two ‘events’ that may be at different locations and different times by using what he called the ‘interval,’ s. It measures the path between events as
s=√[(x²+y²+z²)–(ct)²]. Usually we avoid the square root sign and work with s².”

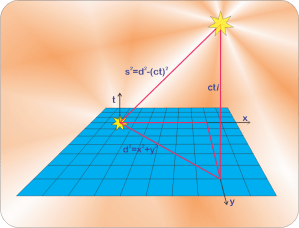
“That minus sign looks weird. Where’d it come from?”

“When Minkowski was designing his spacetime, he needed a time scale that could be combined with the x,y,z lengths but was perpendicular to each of them. Multiplying time by lightspeed c gave a length, but it wasn’t perpendicular. He could get that if he multiplied by i=√(–1) to get cti as a partner for x,y,z. Fortunately, that forced the minus sign into the sum‑of‑squares
(x²+y²+z²)–(ct)² formula.”

Vinnie’s getting impatient. “What is an actual geodesic, who cares about them, and what do these equations have to do with anything?”

“A geodesic is a path in spacetime. Light always travels along a geodesic. The modern version of Newton’s First Law says that any object not subject to an outside force travels along a geodesic. By definition the geodesic is the shortest path, but you can’t select which path from A to B is the shortest unless you can measure or calculate them. There’s math to tell us how to do that. Time’s a given in a Newtonian Universe, not a coordinate, so geodesics are distance‑only. We calculate d along paths that Euclid would recognize as straight lines. That’s why the First Law is usually stated in terms of straight lines.”

“So the lines can go all curvy?”

“Depends, Vinnie. When you’re piloting an over‑water flight, you fly a steady bearing, right?”

“Whenever ATC and the weather lets me. It’s the shortest route.”

“So according to your instruments you’re flying a straight line. But if someone were tracking you from the ISS they’d say you’re flying along a Great Circle, the intersection of Earth’s surface with some planar surface. You prefer Great Circles because they’re shortest‑distance routes. That makes them geodesics for travel on a planetary surface. Each Circle’s a curve when viewed from off the surface.”

“Back to that minus sign, Mr Moire. Why was it fortunate?”

“It’s at the heart of Relativity Theory. The expression links space and time in opposite senses. It’s why space compression always comes along with time dilation.”

“Oh, like at an Event Horizon. Wait, can’t that s²=(x²+y²+z²)–(ct)² arithmetic come out zero or even negative? What would those even mean?”

“The theory covers all three possibilities. If the sum is zero, then the distance between the two events exactly matches the time it would take light to travel between them. If the sum is positive the way I’ve written it then we say the geodesic is ‘spacelike’ because the distance exceeds light’s travel time. If it’s negative we’ve got a ‘timelike’ geodesic; A could signal B with time to spare.”

~ Rich Olcott

The Time Is Out of Joint

On By rolcottIn Cosmology, Crazy Theories, UncategorizedLeave a comment

Vinnie galumphs over to our table. “Hi, guys. Hey, Sy, I just read your Confluence post. I thought that we gave up on things happening simultaneous because of Einstein and relativity but I guess that wasn’t the reason.”

“Oh, things do happen simultaneously, no‑one claims they don’t, it’s just that it’s impossible for two widely‑separated observers to have evidence that two widely‑separated events happened simultaneously. That’s a very different proposition.”

“Ah, that makes me feel better. The ‘nothing is simultaneous‘ idea was making me itchy ’cause I know for sure that a good juggler lets go with one hand just as they’re catching with the other. How’s Einstein involved then?”

“Lightspeed’s a known constant. Knowing distance and lightspeed lets you calculate between‑event time, right? The key to simultaneity was understanding why lightspeed is a constant. We’d known lightspeed wasn’t infinite within the Solar System since Rømer’s time, but people doubted his number applied everywhere. Maxwell’s theory of electromagnetism derived lightspeed from the properties of space itself so it’s universal. Only in Newton’s Universe was it possible for two distant observers to agree that two also‑distant events were simultaneous.”

“Why was Newton’s Universe special?

“Space held still and didn’t bend. Astronomers A and B had a stable baseline between them. After measuring the baseline with light they could measure the angles each observed between the events. Some trigonometry let them send each other congratulatory messages on seeing a simultaneous pair of incidents. After Einstein’s work, they knew better.”

“It’s frames again, ain’t it?”

“Of course, Vinnie. A‘s frame is almost certainly moving relative to B‘s frame. Motion puts the Lorentz relativity factor into the game, making each astronomer’s clock run faster than the other’s. Worse, each astronomer sees that the other’s yardsticks are too short.”

Jeremy gives me a confused look.

“Space compression goes along with time dilation, Jeremy. Professor Hanneken will explain it all when your class gets to that unit. Bottom line, things can happen simultaneously in Einstein’s Universe, but no‑one can agree on which things.”

“Wait, if every frame has its own time‑rate, how can two spaceships rendezvous for an operation?”

“Good question, Jeremy. Einstein had an answer but complications hide under the covers. He suggested that A start a timer when sending a light pulse to a mirror at B. A waits for the reflection. B starts a timer when they see A‘s pulse. A measures the pulse’s round‑trip time. Each creates a clock that advances one tick for half of the round-trip time. B sets their clock back by one tick. That done, they agree to meet some number of ticks later.”

“Hmm… That should work, but you said there are complications.”

“There are always complications. For instance, suppose B is slingshotting around a black hole so that pulse and reflection travel different pathlengths. Or suppose one frame is rotating edge‑on to the other. In practice the ships would re‑sync repeatedly while approaching the rendezvous point.”

Vinnie erupts. “HAW! Successive approximation again!”

“Indeed. If we could extend the method to more than two participants we’d have a true Universal Coordinated Time.”

“Don’t we have that, Mr Moire? The Big Bang happened 14 billion years ago. Couldn’t we measure time from that?”

“Sort of. Last I looked the number was 13.787 plus‑or‑minus 20 million years. Too much slop for an instantaneous fleet‑level rendezvous like the final battle scene in StarTrek:Picard. But you’ve brought up an interesting question for a Crazy Theories seminar. One of Cosmology’s deepest unsolved questions is, ‘How does inertia work?’ Do you remember Newton’s First Law?”

<closes eyes> “In an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.“

“Right. In other words, every object resists change to its current steady motion along a geodesic. Why is that? There’s no coherent, well‑founded, well‑tested theory. Einstein liked Mach’s Principle, which says inertia exists because every object is attracted through space to all the mass in the Universe. Suppose there’s a Mach’s Principle for Time, saying that objects squirt up the Time axis because they’re repelled by all the mass in the Universe.”

Vinnie hoots, “Bo-o-o-ohh-GUS!”

~ Rich Olcott

Hillerman, Pratchett And Narrativium

On By rolcottIn Astronomy, General: Fun Stuff, UncategorizedLeave a comment

No-one else in the place so Jeremy’s been eavesdropping on my conversation with Cal. “Lieutenant Leaphorn says there are no coincidences.”

“Oh, you’ve read Tony Hillerman’s mystery stories then?”

“Of course, Mr Moire. It’s fun getting a sympathetic outsider’s view of what my family and Elders have taught me. He writes Leaphorn as a very wise man.”

“With some interesting quirks for a professional crime solver. He doesn’t trust clues, yet he does trust apparent coincidences enough to follow up on them.”

“It does the job for him, though.”

“Mm‑hm, but that’s in stories. Have you read any of Terry Pratchett’s Discworld books?”

“What are they about?”

From Terry Pratchett’s book
Carpe Jugulum

“Pretty much everything, but through a lens of laughter and anger. Rather like Jonathan Swift. Pratchett was one of England’s most popular authors, wrote more than 40 novels in his too‑brief life. He identified narrativium as the most powerful force in the human universe. Just as the nuclear strong force holds the atomic nucleus together using gluons and mesons, narrativium holds stories together using coincidences and tropes.”

“Doesn’t sound powerful.”

“Good stories, ones that we’d say have legs, absolutely must have internal logic that gets us from one element to the next. Without that narrative flow they just fall apart; no‑one cares enough to remember them. As a writer myself, I’ve often wrestled with a story structure that refused to click together — sparse narrativium — or went in the wrong direction — wayward narrativium.”

“You said ‘the human universe’ like that’s different from the Universe around us.”

“The story universe is a multiverse made of words, pictures and numbers, crafted by humans to explain why one event follows another. The events could be in the objective world made of atoms or within the story world itself. Legal systems, history, science, they’re all pure narrativium. So is money, mostly. We don’t know of anything else in the Universe that builds stories like we do.”

“How about apes?”

“An open question, especially for orangutans. One of Pratchett’s important characters is The Librarian, a university staff member who had accidentally been changed from human to orangutan. He refuses to be restored because he prefers his new form. Which gives you a taste of Pratchett’s humor and his high regard for orangutans. But let’s get back to Leaphorn and coincidences.”

“Regaining control over your narrativium, huh?”

“Guilty as charged. Leaphorn’s standpoint is that there are no coincidences because the world runs on patterns, that events necessarily connect one to the next. When he finds the pattern, he solves the mystery.”

“Very Diné. Our Way is to look for and restore harmony and balance.”

“Mm‑hm. But remember, Leaphorn is only a character in Hillerman’s narrativium‑driven stories. The atom‑world may not fit that model. A coincidence for you may not be a coincidence for someone else, depending. Those two concurrent June novas, for example. For most of the Universe they’re not concurrent.”

“I hope this doesn’t involve relativistic clocks. Professor Hanneken hasn’t gotten us to Einstein’s theories yet.”

Adapted from images by
IAU and Sky & Telescope magazine
(Roger Sinnott & Rick Fienberg)
CC BY 3.0

“No relativity; this is straight geometry. Rømer could have handled it 350 years ago.” <brief tapping on Old Reliable’s screen> “Here’s a quick sketch and the numbers are random. The two novas are connected by the blue arc as we’d see them in the sky if we were in Earth’s southern hemisphere. We live in the yellow solar system, 400 lightyears from each of them so we see both events simultaneously, 400 years after they happened. We call that a coincidence and Cal’s skywatcher buddies go nuts. Suppose there are astronomers on the white and black systems.”

<grins> “Those four colors aren’t random, Mr Moire.”

<grins back> “Caught me, Jeremy. Anyway, the white system’s astronomers see Vela’s nova 200 years after they see the one in Lupus. The astronomers in the black system record just the reverse sequence. Neither community even thinks of the two as a pair. No coincidence for them, no role for narrativium.”

~ Rich Olcott

  • This is the 531st post in an unbroken decade‑long weekly series that I originally thought might keep going for 6 months. <whew!>

Confluence

On By rolcottIn Astronomy, Astronomy: Multi-messenger, General: Fun Stuff, UncategorizedLeave a comment

“My usual cup of — Whoa! Jeremy, surprised to see you behind the counter here. Where’s Cal?”

“Hi, Mr Moire. Cal just got three new astronomy magazines in the same delivery so he’s over there bingeing. He said if I can handle the pizza place gelato stand he can trust me with his coffee and scones. I’m just happy to get another job ’cause things are extra tough back on the rez these days. Here’s your coffee, which flavor scone can I get for you?”

“Thanks, Jeremy. Smooth upsell. I’ll take a strawberry one. … Morning, Cal. Having fun?”

“Morning, Sy. Yeah, lotsa pretty pictures to look at. Funny coincidence, all three magazines have lists of coincidences. This one says February 23, 1987 we got a neutrino spike from supernova SN 1987A right after we saw its light. The coincidence told us that neutrinos fly almost fast as light so the neutrino’s mass gotta be pretty small. 1987’s also the year the Star Tours Disney park attractions opened for the Star Wars fans. The very same year Gene Roddenberry and the Paramount studio released the first episodes of Star Trek: The Next Generation. How about that?”

“Pretty good year.”

“Mm‑hm. Didja know here in 2025 we’ve got that Mercury‑Venus‑Jupiter-Saturn‑Uranus‑Neptune straight‑line arrangement up in the sky and sometimes the Moon lines up with it?”

“I’ve read about it.”

“Not only that, but right at the September equinox, Neptune’s gonna be in opposition. That means our rotation axis will be broadside to the Sun just as Neptune will be exactly behind us. It’ll be as close to us as it can get and it’s face‑on to the Sun so it’s gonna be at its brightest. Cool, huh?”

“Good time for Hubble Space Telescope to take another look at it.”

“Those oughta be awesome images. Here’s another coincidence — Virgo’s the September sign, mostly, and its brightest star is Spica. All the zodiac constellations are in the ecliptic plane where all the planet orbits are. Planets can get in the way between us and Spica. The last planet to do that was Venus in 1783. The next planet to do that will be Venus again, in 2197.”

“That’ll be a long wait. You’ve read off things we see from Earth. How about interesting coincidences out in the Universe?”

“Covered in this other magazine’s list. Hah, they mention 1987, too, no surprise. Ummm, in 2017 the Fermi satellite’s GRB instrument registered a gamma‑ray burst at the same time that LIGO caught a gravitational wave from the same direction. With both light and gravity in the picture they say it was two neutron stars colliding.”

“Another exercise in multi-messenger astronomy. Very cool.”

“Ummm … Galaxy NGC 3690 shot off two supernovas just a few months apart last year. Wait, that name’s familiar … Got it, it’s half of Arp 299. 299’s a pair of colliding galaxies so there’s a lot of gas and dust and stuff floating around to set off stars that are in the brink. If I remember right, we’ve seen about eight supers there since 2018.”

“Hmm, many events with a common cause. Makes sense.”

“Oh, it’s a nice idea, alright, but explain V462 Lupi and V572 Velorum. Just a couple months ago, two novas less than 2 weeks apart in two different constellations 20 degrees apart in the sky. Bright enough you could see ’em both with good eyes if you were below the Equator and knew where to look and looked in the first week of June. My skywatcher internet buddies down there went nuts.”

“How far are those events from us?”

“The magazine doesn’t say. Probably the astronomers are still working on it. Could be ten thousand lightyears, but I’d bet they’re a lot closer than that.”

“On average, visible stars are about 900 lightyears away. Twenty degrees would put them about 300 lightyears apart. They’re separated by a slew of stars that haven’t blown up. One or both could be farther away than that, naturally. Whatever, it’s hard to figure a coordinating cause for such a distant co‑occurrence. Sometimes a coincidence is just a coincidence.”

Adapted from images by
IAU and Sky & Telescope magazine
(Roger Sinnott & Rick Fienberg)
CC BY 3.0

~ Rich Olcott

Up, Down And Between

On By rolcottIn Physics: Entropy and Thermodynamics, Uncategorized1 Comment

Vinnie finishes his double‑pepperoni pizza. “Sy, these enthalpies got a pressure‑volume part and a temperature‑heat capacity part, but seems to me the most important part is the chemical energy.”

I’m still working on my slice (cheese and sausage). “That’s certainly true from a fuel engineering perspective, Vinnie. Here’s a clue. Check the values in this table for 0°C, also known as 273K.”

Link to Larger image

“Waitaminute! That line says the enthalpy’s exactly zero under the book‘s conditions. We talked about zeros a long time ago. All measurements have error. Nothing’s exactly zero unless it’s defined that way or it’s Absolute Zero temperature and we’ll never get there. Is this another definition thing?”

“More of a convenience thing. The altimeters in those planes you fly, do they display the distance to Earth’s center?”

“Nope, altitude above sea level, if they’re calibrated right.”

“But the other would work, too, say as a percentage of the average radius?”

“Not really. Earth’s fatter at the Equator than it is at the poles. You’d always have to correct for latitude. And the numbers would be clumsy, always some fraction of a percent of whatever the average is—”

“6371 kilometers.”

“Yeah, that. Try working with fractions of a part per thousand when you’re coming in through a thunderstorm. Give me kilometers or feet above sea level and I’m a lot happier.”

“But say you’re landing in Denver, 1.6 kilometers above sea level.”

“It’s a lot easier to subtract 1.6 from baseline altitude in kilometers than 0.00025 from 1.00something and getting the decimals right. Sea‑level calibrations are a lot easier to work with.”

“So now you know why the book shows zero enthalpy for water at 273K.”

“You’re saying there’s not really zero chemical energy in there, it’s just a convenient place to start counting?”

“That’s exactly what I’m saying. Chemical energy is just another form of potential energy. Zeroes on a potential scale are arbitrary. What’s important is the difference between initial and final states. Altitude’s about gravitational potential relative to the ground; chemists care about chemical potential relative to a specific reaction’s final products. Both concerns are about where you started and where you stop.”

“Gimme a chemical f’rinstance.”

<reading off of Old Reliable> “Reacting 1 gram of oxygen gas and 0.14 gram of hydrogen gas slowly in a catalytic fuel cell at 298K and atmospheric pressure produces one gram of liquid water and releases 18.1 kilojoules of energy. Exploding the same gas mix at the same pressure in a piston also yields 18.1 kilojoules once you cool everything back down to 298K. Different routes, same results.”

Meanwhile, Jeremy’s wandered over from his gelato stand. “Excuse me, Mr Moire. I read your Crazy Theory about how mammals like to keep their body temperature in the range near water’s minimum Specific Heat, um Heat Capacity, but now I’m confused.”

“What’s the confusion, Jeremy?”

“Well, what you told me before made sense, about increased temperature activates higher‑energy kinds of molecular waggling to absorb the heat. But that means that Heat Capacity always ought to increase with increasing temperature, right?”

“Good thinking. So your problem is…?

“Your graph shows that if water’s cold, warming it decreases its Heat Capacity. Do hotter water molecules waggle less?”

“No, it’s a context thing. Gas and liquid are different contexts. Each molecule in a gas is all by itself, most of the time, so its waggling is determined only by its internal bonding and mass configuration. Put that molecule into a liquid or solid, it’s subject to what its neighbors are doing. Water’s particularly good at intermolecular interactions. You know about the hexagonal structure locked into ice and snowflakes. When water ice melts but it’s still at low temperature, much of the hexagonal structure hangs around in a mushy state. A loose structure’s whole‑body quivering can absorb heat energy without exciting waggles in its constituent molecules. Raising the temperature disrupts that floppy structure. That’s most of the fall on the Heat Capacity curve.”

“Ah, then the Sensitivity decrease on the high‑temperature side has to do with blurry structure bits breaking down to tinier pieces that warm up more from less energy. Thanks, Mr Moire.”

“Don’t mention it.”

~~ Rich Olcott

The Trough And The Plateau

On By rolcottIn Astronomy: Planetary Science, Mathematics, UncategorizedLeave a comment

Particularly potent pepperoni on Pizza Eddie’s special tonight so I dash to the gelato stand. “Two dips of pistachio in a cup, please, Jeremy, and hurry. Hey, why the glum look?”

“The season’s moving so slowly, Mr Moire. I’m a desert kid, used to bright skies. I need sunlight! We’re getting just a few hours of cloudy daylight each day. It seems like we’re never gonna leave this pattern. Here’s your gelato.”

“Thanks. Sorry about the cloudiness, it’s the wintertime usual around here. But you’re right, we’re on a plateau.”

“Nosir, the Plateau’s the Four Corners area, on the other side of the Rockies, miles and miles away from here.”

<chuckle> “Not the Colorado Plateau, the darkness plateau. Or the daylight trough, if you prefer. Buck up, we’ll get a daylight plateau starting in a few months.” <unholstering Old Reliable> “Here’s a plot of daylight hours through the year at various northern latitudes. We’re in between the red and green curves. For folks south of the Equator that’d just turn upside‑down, of course. I added a star at today’s date in mid‑December, see. We’re just shy of the winter solstice; the daylight hours are approaching the minimum. You’re feeling stressed because these curves don’t change much day-to-day near minimum or maximum. In a couple of weeks the curve will bend upwards again. Come the Spring equinox, you’ll be shocked at how rapidly the days lengthen.”

“Yeah, my Mom says I’m too impatient. She says that a lot. Okay, above the Arctic Circle they’ve got months‑long night and then months‑long day, I’ve read about that. I hadn’t realized it was a one‑day thing at the Circle. Hey, look at the straight lines leading up to and away from there. Is that the Summer solstice? Those low‑latitude curves look like sine waves. Are they?”

“Summer solstice in the northern hemisphere, Winter solstice for the southerners. The curves are distorted sines. Ready for a surprise?”

<Looks around the nearly empty eatery.> “With business this slow I’m just sitting here so I’m bored. Surprise me, please.”

“Sure. One of the remarkable things about a sine wave is, when you graph its slopes you get another sine wave shifted back a quarter. Here, check it out.”

“Huh! When the sine wave’s mid-climb, the slope’s at its peak. When the sine wave’s peaking, the slope’s going through zero on the way down. And they do have exactly the same shape. I see where you’re going, Mr Miore. You’re gonna show me the slopes of the daylight graphs to see if they’re really sine waves.”

“You’re way ahead of me and Old Reliable, Jeremy.” <frantic tapping on OR’s screen> “There, point‑by‑point slopes for each of the graphs. Sorta sine‑ish near the Equator but look poleward.”

“The slopes get higher and flatter until the the Arctic Circle line suddenly drops down to flip its sign. Those verticals are the solstices, right?”

“Right. Notice that even at the Circle the between‑solstice slopes aren’t quite constant so the straight lines you eye‑balled aren’t quite that. North of the Circle the slopes go nuts because of the abrupt shifts between varying and constant sun.”

Link to larger image

“How do you get these curves, Mr Moire?”

“It’s a series of formulas. Dust off your high school trig. The Solar Declination Angle equation is about the Sun’s height above or below the horizon. It depends on Earth’s year length, its axial tilt and the relative date, t=T‑T0. For these charts I set T0 to the Spring equinox. If the height’s negative the Sun’s below the horizon, okay?”

“Sine function is opposite‑over‑hypotenuse and the height’s opposite alright or we’d burn up, yup.”

“The second formula gives the the Hour Angle between your longitude and whichever longitude has the Sun at its zenith.”

“Why would you want that?”

“Because it’s the heart of the duration formula. When you roll all three formulas together you get one big expression that gives daylight duration in terms of Earth’s constants, time of year and your location. That’s what I plotted.”

“How about the slope curves?”

“Calculus, Jeremy, d/dt of that combined duration function. It’s beyond my capabilities but Old Reliable’s up to it.”

~ Rich Olcott

Rumford’s Boring Story

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Okay, Mr Moire, my grandfather’s engineering handbook has Specific Heat tables because Specific Heat measures molecular wabbling. If he’s got them, though, why’s Enthalpy in the handbook, too?”

“Enthalpy’s not my favorite technical term, Jeremy. It’s wound up in a centuries‑old muddle. Nobody back then had a good, crisp notion of energy. Descartes, Leibniz, Newton and a host of German engineers and aristocratic French hobby physicists all recognized that something made motion happen but everyone had their own take on what that was and how to calculate its effects. They used a slew of terms like vis viva, ‘quantity of motion,’ ‘driving force,’ ‘quantity of work,’ a couple of different definitions of ‘momentum‘ — it was a mess. It didn’t help that a lot of the argument went on before Euler’s algebraic notations were widely adopted; technical arguments without math are cumbersome and can get vague and ambiguous. Lots of lovely theories but none of them worked all that well in the real world.”

“Isn’t that usually what happens? I always have problems in the labs.”

“You’re not alone. Centuries ago, Newton’s Laws of Motion and Gravity made good predictions for planets, not so good for artillery trajectories. Gunners always had to throw in correction factors because their missiles fell short. Massachusetts‑born Benjamin Thompson, himself an artilleryman, found part of the reason.”

“Should I know that name?”

“In later years he became Count Rumford. One of those people who get itchy if they’re not creating something. He was particularly interested in heat — how to trap it and how to make it go where you want.”

“Wait, he was an American but he was a Count? I thought that was illegal.”

“Oh, he left the States before they were the States. During the Revolution he organized a Royalist militia in New York and then lit out for Europe. The Bavarians made him a Count after he spent half‑a‑dozen years doing creative things like reorganizing their army, building public works and introducing potato farming. He concocted a nourishing soup for the poor and invented the soup line for serving it up. But all this time his mind was on a then‑central topic of Physics — what is heat?”

“That was the late 1700s? When everyone said heat was some sort of fluid they called ‘caloric‘?”

“Not everyone, and in fact there were competing theories about caloric — an early version of the particle‑versus‑wave controversy. For a while Rumford even supported the notion that ‘frigorific’ radiation transmitted cold the same way that caloric rays transmitted heat. Whatever, his important contributions were more practical and experimental than theoretical. His redesign of the common fireplace was such an improvement that it took first England and then Europe by storm. Long‑term, though, we remember him for a side observation that he didn’t think important enough to measure properly.”

“Something to do with heat, I’ll bet.”

“Of course. As a wave theory guy, Rumford stood firmly against the ‘caloric is a fluid‘ camp. ‘If heat is material,‘ he reasoned, ‘then a heat‑generating process must eventually run out of caloric.’ He challenged that notion by drilling out a cannon barrel while it was immersed in cold water. A couple of hours of steady grinding brought the water up to boiling. The heating was steady, too, and apparently ‘inexhaustible.’ Better yet, the initial barrel, the cleaned‑out barrel and the drilled‑out shavings all had the same specific heat so no heat had been extracted from anything. He concluded that heat is an aspect of motion, totally contradicting the leading caloric theories and what was left of phlogiston.”

<chuckle> “He was a revolutionary, after all. But what about ‘Enthalpy‘?”

“Here’s an example. Suppose you’ve got a puddle of gasoline, but its temperature is zero kelvins and somehow it’s compressed to zero volume. Add energy to those waggling molecules until the puddle’s at room temperature. Next, push enough atmosphere out of the way to let the puddle expand to its normal size. Pushing the atmosphere takes energy, too — the physicists call that ‘PV work‘ because it’s calculated as the pressure times the volume. The puddle’s enthalpy is its total energy content — thermal plus PV plus the chemical energy you get when it burns.”

~~ Rich Olcott

It’s in The Book

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, Physics: Quantum Mechanics, UncategorizedLeave a comment

A young man’s knock, eager yet a bit hesitant. “Door’s open, Jeremy, c’mon in.”

“Hi, Mr Moire, I’ve got something to show you. It’s from my acheii, my grandfather. He said he didn’t need it any more now he’s retired so he gave it to me. What do you think?”

“Wow, the CRC Handbook of Chemistry And Physics, in the old format, not the 8½×11″ monster. An achievement award, too — my congratulations to your grandfather. Let’s see … over 3000 pages, and that real thin paper you can read through. It’s still got the math tables in front — they moved those to an Appendix by the time I bought my copy. Oooh yeah, lots of data in here, probably represents millions of grad student lab hours. Tech staff, too. And then their bosses spent time checking the work before publishing.”

“Acheii said I’d have to learn a lot before I could use it properly. I see lots of words in there I don’t recognize.” <opens book to a random page> “See, five- and six‑figure values for, what’re Specific Heat and Enthalpy?”

“Your grandfather’s absolutely correct. Much of the data’s extremely specialized. Most techs, including me, have a few personal‑favorite sections they use a lot, never touch the rest of the book. These particular pages, for instance, would be gold for a someone who designs or operates steam‑driven equipment.”

“But what do these numbers mean?”

“Specific Heat is the amount of heat energy you need to put into a certain mass of something in order to raise its temperature by a certain amount. In the early days the Brits, the Scots really, defined the British Thermal Unit as the amount of energy it took to raise the temperature of one pound of liquid water by one degree Fahrenheit. You’d calculate a fuel purchase according to how many BTUs you’d need. Science work these days is metric so these pages tabulate Specific Heat for a substance in joules per gram per °C. Tech in the field moves slow so BTUs are still popular inside the USA and outside the lab.”

“But these tables show different numbers for different temperatures and they’re all for water. Why water? Why isn’t the Specific Heat the same number for every temperature?”

“Water’s important because most power systems use steam or liquid water as the working fluid or coolant. Explaining why heat capacity varies with temperature was one of the triumphs of 19th‑century science. Turns out it’s all about how atomic motion but atoms were a controversial topic at the time. Ostwald, for instance—”

“Who?”

“Wilhelm Ostwald, one of science’s Big Names in the late 1800s. Chemistry back then was mostly about natural product analysis and seeing what reacted with what. Ostwald put his resources into studying chemical processes themselves, things like crystallization and catalysis. He’s regarded as the founder of Physical Chemistry. Even though he invented the mole he steadfastly maintained that atoms and molecules were nothing more than diffraction‑generated illusions. He liked a different theory but that one didn’t work out.”

“Too bad for him.”

“Oh, he won the first Nobel Prize in Chemistry so no problem. Anyway, back to Specific Heat. In terms of its molecules, how do you raise something’s temperature?”

“Um, temperature’s average kinetic energy, so I’d just make the molecules move faster.”

“Well said, except in the quantum world there’s another option. The molecules can’t just waggle any which way. There are rules. Different molecules do different waggles. Some kinds of motion take more energy to excite than others do. Rule 1 is that the high‑energy waggles don’t get to play until the low‑energy ones are engaged. Raising the temperature is a matter of activating more of the high‑energy waggles. Make sense?”

“Like electron shells in an atom, right? Filling the lowest‑energy shells first unless a photon supplies more energy?”

“Exactly, except we’re talking atoms moving within a molecule. Smaller energies, by a factor of 100 or more. My point is, the heat capacity of a substance depends on which waggles activate as the temperature rises. We didn’t understand heat capacity until we applied quantum thinking to the waggles.”

“What about ‘Enthalpy’ then?”

Crystal photo by JJ Harrison

~ Rich Olcott

Mushy stuff

On By rolcottIn Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

“Amanda! Amanda! Amanda!”

“All right, everyone, settle down for our final Crazy Theorist. Jim, you’re up.”

“Thanks, Cathleen. To be honest I’m a little uncomfortable because what I’ve prepared looks like a follow-on to Newt’s idea but we didn’t plan it that way. This is about something I’ve been puzzling over. Like Newt said, black holes have mass, which is what everyone pays attention to, and charge, which is mostly unimportant, and spin. Spin’s what I’ve been pondering. We’ve all got this picture of a perfect black sphere, so how do we know it’s spinning?”

Voice from the back of the room — “Maybe it’s got lumps or something on it.”

“Nope. The No-hair Theorem says the event horizon is mathematically smooth, no distinguishing marks or tattoos. Question, Jeremy?”

“Yessir. Suppose an asteroid or something falls in. Time dilation makes it look like it’s going slower and slower as it gets close to the event horizon, right? Wouldn’t the stuck asteroid be a marker to track the black hole’s rotation?”

“Excellent question.” <Several of Jeremy’s groupies go, “Oooh.”> “Two things to pay attention to here. First, if we can see the asteroid, it’s not yet inside the horizon so it wouldn’t be a direct marker. Beyond that, the hole’s rotation drags nearby spacetime around with it in the ergosphere, that pumpkin‑shaped region surrounding the event horizon except at the rotational poles. As soon as the asteroid penetrates the ergosphere it gets dragged along. From our perspective the asteroid spirals in instead of dropping straight. What with time dilation, if the hole’s spinning fast enough we could even see multiple images of the same asteroid at different levels approaching the horizon.”

Jeremy and all his groupies go, “Oooh.”

“Anyhow, astronomical observation has given us lots of evidence that black holes do spin. I’ve been pondering what’s spinning in there. Most people seem to think that once an object crosses the event horizon it becomes quantum mush. There’d be this great mass of mush spinning like a ball. In fact, that was Schwarzchild’s model for his non-rotating black hole — a simple sphere of incompressible fluid that has the same density throughout, even at the central singularity.”

VBOR — “Boring!”

“Well yeah, but it might be correct, especially if spaghettification and the Firewall act to grind everything down to subatomic particles on the way in. But I got a different idea when I started thinking about what happened to those two black holes that LIGO heard collide in 2015. It just didn’t seem reasonable that both of those objects, each dozens of solar masses in size, would get mushed in the few seconds it took to collide. Question, Vinnie?”

“Yeah, nice talk so far. Hey, Sy and me, we talked a while ago about you can’t have a black hole inside another black hole, right, Sy?”

“That’s not quite what I said, Vinnie. What I proved was that after two black holes collide they can’t both still be black holes inside the big one. That’s different and I don’t think that’s where Jim’s going with this.”

“Right, Mr Moire. I’m not claiming that our two colliders retain their black hole identities. My crazy theory is that each one persists as a high‑density nubbin in an ocean of mush and the nubbins continue to orbit in there as gravity propels them towards the singularity.”

VBOR —”Orbit? Like they just keep that dance going after the collision?”

“Sure. What we can see of their collision is an interaction between the two event horizons and all the external structures. From the outside, we’d see a large part of each object’s mass eternally inbound, locked into the time dilation just above the joined horizon. From the infalling mass perspective, though, the nubbins are still far apart. They collide farther in and farther into the future. The event horizon collision is in their past, and each nubbin still has a lot of angular momentum to stir into the mush. Spin is stirred-up mush.”

Cathleen’s back at the mic. “Well, there you have it. Amanda’s male-pattern baldness theory, Newt’s hyper‑planetary gear, Kareem’s purple snowball or Jim’s mush. Who wins the Ceremonial Broom?”

The claque responds — “Amanda! Amanda! Amanda!”

~ Rich Olcott

Virial Yang And Yin

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“But Mr Moire, how does the Virial Equation even work?”

“Sometimes it doesn’t, Jeremy. There’s an ‘if’ buried deep in the derivation. It only works for a system in equilibrium. Sometimes people use the equation as a test for equilibrium.”

“Sorry, what does that mean?”

“Let’s take your problem galaxy cluster as an example. Suppose the galaxies are all alone in the Universe and far apart even by astronomical standards. Gravity’s going to pull them together. Galaxy i and galaxy j are separated by distance Rij. The potential energy in that interaction is Vij = G·mi·mj / Rij. The R‘s are very large numbers in this picture so the V attractions are very small. The Virial is the average of all the V’s so our starting Virial is nearly zero.”

“Nearly but not quite zero, I get that. Wait, if the potential energy starts near zero when things are far apart, and a falling‑in object gives up potential energy, then whatever potential energy it still has must go negative.”

“It does. The total energy doesn’t change when potential energy converts to kinetic energy so yes, we say potential energy decreases even though the negative number’s magnitude gets larger. It’d be less confusing if we measured potential energy going positive from an everything-all-together situation. However, it makes other things in Physics much simpler if we simply write (change in potential energy)+(change in kinetic energy)=0 so that’s the convention.”

“The distances do eventually get smaller, though.”

“Sure, and as the objects move closer they gain momentum and kinetic energy. Gaining momentum is gaining kinetic energy. You’re used to writing kinetic energy as T=m·v²/2, but momentum is p=m·v so it’s just as correct to write T=p²/2m. The two are different ways of expressing the same quantity. When a system is in equilibrium, individual objects may be gaining or losing potential energy, but the total potential energy across the system has reached its minimum. For a system held together by gravity or electrostatic forces, that’s when the Virial is twice the average kinetic energy. As an equation, V+2T=0.”

“So what you’re saying is, one galaxy might fall so far into the gravity well that its potential energy goes more negative than –2T. But if the cluster’s in equilibrium, galaxy‑galaxy interactions during the fall‑in process speed up other galaxies just enough to make up the difference. On the flip side, if a galaxy’s already in deep, other galaxies will give up a little T to pull it outward to a less negative V.”

“Well stated.”

“But why 2? Why not 3½ or some other number?”

“The 2 comes from the kinetic energy expression’s ½. The multiplier could change depending on how the potential energy varies with distance. For both gravity and electrostatic interactions the potential energy varies the same way and 2 is fine the way it is. In a system with a different rule, say Hooke’s Law for springs and rubber bands, the 2 gets multiplied by something other than unity.”

“All that’s nice and I see how the Virial Equation lets astronomers calculate cluster‑average masses or distances from velocity measurements. I suppose if you also have the masses and distances you can test whether or not a collection of galaxies is in equilibrium. What else can we do with it?”

“People analyze collections of stars the same way, but Professor Hanneken’s a physicist, not an astronomer. He wouldn’t have used class time on the Virial if it weren’t good for a broad list of phenomena in and outside of astronomy. Quantum mechanics, for instance. I’ll give you an important example — the Sun.”

“One star, all by itself? Pretty trivial to take its average.”

“Not averaging the Sun as an object, averaging its plasma contents — hydrogen nuclei and their electrons, buffeted by intense heat all the way down to the nuclear reactions that run near the Sun’s core. It’s gravitational potential energy versus kinetic energy all over again, but at the atomic level this time. The Virial Theorem still holds, even though turbulence and electromagnetic effects generate a complicated situation.”

“I’m glad he didn’t assign that as a homework problem.”

“The semester’s not over yet.”

~~ Rich Olcott