Tag: Lorentz factor

Does Tomorrow Exist?

On By rolcottIn Cosmology, General: Fun Stuff, UncategorizedLeave a comment

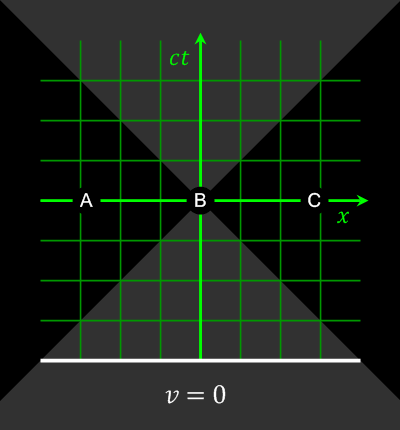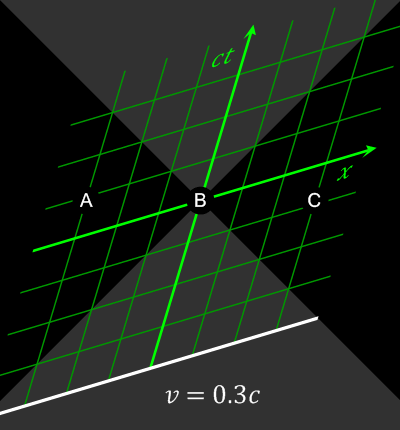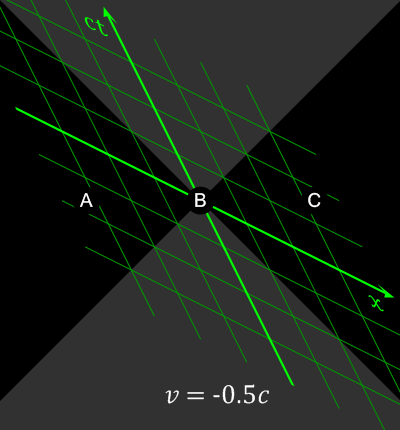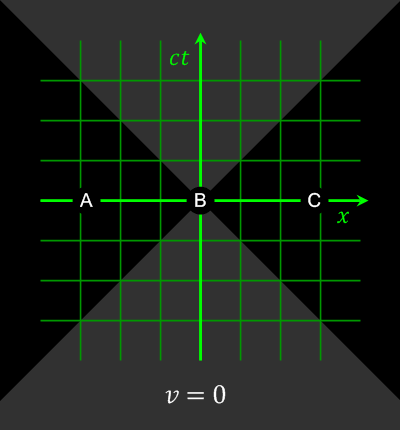
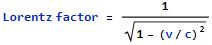Power’s back on. The elevator lets us out on the second floor where we proceed into Eddie’s Pizza Place. We order, find a table, and Cathleen cocks an eyebrow. “So, Anne, you’re a time‑traveler?”

“Lots of dimensions, actually. Time, space, probability… Once I accidentally jumped into a Universe where the speed of light was a lot slower. I was floating near a planet in a small system whose sun flared up but it took a long, long time for the flash to reflect off the planet behind me. Funny, I felt stiffer than usual. It was a lot harder to move my arms. I avoid cruising dimensions like that one.”

<The other eyebrow goes up> “Wait, what’s the speed of light got to do with dimensions? And why would it affect moving your arms?”

My cue. “Physics has a long‑standing problem with the speed of light and a dozen or so other fundamental numbers like Newton’s gravitational constant and Einstein’s cosmological constant. We can measure them but we can’t explain why they have the values they do. Okay, the speed of light depends on electric and magnetic force constants, but we can’t explain those, either — the rabbit hole just gets deeper. In practice, our Laws of Physics are a set of equations with blanks for plugging in the measured values. People have suggested that there’s a plethora of alternate universes with the same laws of physics we have but whose fundamental constants can vary from ours. Apparently Anne traveled along a dimension that connects universes with differing values of lightspeed.”

“I suppose. … But the arm‑moving part?”

“An effect of Special Relativity. Newton’s Second Law a=F/m says that an object’s acceleration equals the applied force per unit mass. That works fine in every‑day life but not when the object’s velocity gets close to lightspeed.” <jotting on a paper napkin> “I don’t see Vinnie nearby so here’s the relativistic equation: a=(F/m)×√[1–(v/c)²]. The v/c ratio compares object velocity to lightspeed. The Lorentz factor, that square root, is less than 1.0 for velocities less than lightspeed. This formula says a given amount of force per unit mass produces less acceleration than Newton would expect. How much less depends on how fast you’re already going. In fact, the acceleration boost approaches zero when v approaches c. With me?”

“If your factor’s exactly zero, then even an infinite force couldn’t accelerate you, right? But what’s all that got to do with my arm?”

“Zero acceleration, mm‑hm. Suppose your arm’s rest mass and muscle force per unit mass are the same in the slow‑light universe as they are in ours. The Lorentz factor’s different. Lightspeed in our Universe is 3×108 m/s. Suppose you wave your arm at 10 m/s. Your Lorentz factor here is √[1–(10/3×108)²] which is so close to unity we couldn’t measure the difference. Now suppose ‘over there’ the lightspeed is 20 m/s and you try the same wave. The Lorentz formula works out to √[1–(10/20)²] or about 85%. That wave would cost you about 15% more effort.”

<Both eyebrows down> “Have you tried going forward in time?”

“Sure, but I can’t get very far. It’s like I’ve got an anchor ‘here.’ I can move back ‘here’ from the past, no problem, but when I try to move forward from ‘here’ even a day or so … It’s hard to describe but as I go everything feels fuzzier and then I get queasy and have to stop. Do you have an explanation for that, Sy?”

“Well, an explanation but I can’t tell you it’s correct. Einstein thought it conflicts with Relativity, other people disagree. According to the growing block theory of time, the past and present are set and unchanging but the future doesn’t exist until we get there. Your description sounds like a build on that theory, like maybe the big structures extend a bit beyond us but their quantum details are still chaotic until time catches up with them. There are a few reports of lab experiments that would be consistent with something like that but it’s early days in the research.”

“As the saying goes, ‘Time will tell,’ right, Sy?”

“Mm-hm, lo que será, será.“

~ Rich Olcott

A No-Charge Transaction

On By rolcottIn Cosmology, Crazy Theories, Physics: Light and Relativity, UncategorizedLeave a comment

“I ain’t done yet, Sy. I got another reason for Dark Matter being made of faster‑then‑light tachyons.”

“I’m still listening, Vinnie.”

“Dark Matter gotta be electrically neutral, right, otherwise it’d do stuff with light and that doesn’t happen. I say tachyons gotta be neutral.”

“Why so?”

“Stands to reason. Suppose tachyons started off as charged particles. The electric force pushes and pulls on charges hugely stronger than gravity pulls—”

“1036 times stronger at any given distance.”

“Yeah, so right off the bat charged tachyons either pair up real quick or they fly away from the slower‑than‑light bradyon neighborhood leaving only neutral tachyons behind for us bradyon slowpokes to look at.”

“But we’ve got un‑neutral bradyon matter all around us — electrons trapped in Earth’s Van Allen Belt and Jupiter’s radiation belts, for example, and positive and negative plasma ions in the solar wind. Couldn’t your neutral tachyons get ionized?”

“Probably not much. Remember, tachyon particles whiz past each other too fast to collect into a star and do fusion stuff so there’s nobody to generate tachyonic super‑high‑energy radiation that makes tachyon ions. No ionized winds either. If a neutral tachyon collides with even a high-energy bradyon, the tachyon carries so much kinetic energy that the bradyon takes the damage rather than ionize the tachyon. Dark Matter and neutral tachyons both don’t do electromagnetic stuff so Dark Matter’s made of tachyons.”

“Ingenious, but you missed something way back in your initial assumptions.”

“Which assumption? Show me.”

“You assumed that tachyon mass works the same way that bradyon mass does. The math says it doesn’t.” <grabbing scratch paper for scribbling> “Whoa, don’t panic, just two simple equations. The first relates an object’s total energy E to its rest mass m and its momentum p and lightspeed c.”

E² = (mc²)² + (pc)²

“I recognize the mc² part, that’s from Einstein’s Equation, but what’s the second piece and why square everything again?”

“The keyword is rest mass.”

“Geez, it’s frames again?”

“Mm‑hm. The (mc²)² term is about mass‑energy strictly within the object’s own inertial frame where its momentum is zero. Einstein’s famous E=mc² covers that special case. The (pc)² term is about the object’s kinetic energy relative to some other‑frame observer with relative momentum p. When kinetic energy is comparable to rest‑mass energy you’re in relativity territory and can’t just add the two together. The sum‑of‑squares form makes the arithmetic work when two observers compare notes. Can I go on?”

“I’m still waitin’ to hear about tachyons.”

“Almost there. If we start with that equation, expand momentum as mass times velocity and re‑arrange a little, you get this formula

E = mc² / √(1 – v²/c²)

The numerator is rest‑mass energy. The v²/c² measures relative kinetic energy. The Lorentz factor down in the denominator accounts for that. See, when velocity is zero the factor is 1.0 and you’ve got Einstein’s special case.”

“Give me a minute. … Okay. But when the velocity gets up to lightspeed the E number gets weird.”

“Which is why c is the upper threshold for bradyons. As the velocity relative to an observer approaches c, the Lorentz factor approaches zero, the fraction goes to infinity and so does the object’s energy that the observer measures.”

“Okay, here’s where the tachyons come in ’cause their v is bigger than c. … Wait, now the equation’s got the square root of a negative number. You can’t do that! What does that even mean?”

“It’s legal, when you’re careful, but interpretation gets tricky. A tachyon’s Lorentz factor contains √(–1) which makes it an imaginary number. However, we know that the calculated energy has to be a real number. That can only be true if the tachyon’s mass is also an imaginary number, because i/i=1.”

“What makes imaginary energy worse than imaginary mass?”

“Because energy’s always conserved. Real energy stays that way. Imaginary mass makes no sense in Newton’s physics but in quantum theory imaginary mass is simply unstable like a pencil balanced on its point. The least little jiggle and the tachyon shatters into real particles with real kinetic energy to burn. Tachyons disintegrating may have powered the Universe’s cosmic inflation right after the Big Bang — but they’re all gone now.”

“Another lovely theory shot down.”

~ Rich Olcott

The Time Is Out of Joint

On By rolcottIn Cosmology, Crazy Theories, UncategorizedLeave a comment

Vinnie galumphs over to our table. “Hi, guys. Hey, Sy, I just read your Confluence post. I thought that we gave up on things happening simultaneous because of Einstein and relativity but I guess that wasn’t the reason.”

“Oh, things do happen simultaneously, no‑one claims they don’t, it’s just that it’s impossible for two widely‑separated observers to have evidence that two widely‑separated events happened simultaneously. That’s a very different proposition.”

“Ah, that makes me feel better. The ‘nothing is simultaneous‘ idea was making me itchy ’cause I know for sure that a good juggler lets go with one hand just as they’re catching with the other. How’s Einstein involved then?”

“Lightspeed’s a known constant. Knowing distance and lightspeed lets you calculate between‑event time, right? The key to simultaneity was understanding why lightspeed is a constant. We’d known lightspeed wasn’t infinite within the Solar System since Rømer’s time, but people doubted his number applied everywhere. Maxwell’s theory of electromagnetism derived lightspeed from the properties of space itself so it’s universal. Only in Newton’s Universe was it possible for two distant observers to agree that two also‑distant events were simultaneous.”

“Why was Newton’s Universe special?

“Space held still and didn’t bend. Astronomers A and B had a stable baseline between them. After measuring the baseline with light they could measure the angles each observed between the events. Some trigonometry let them send each other congratulatory messages on seeing a simultaneous pair of incidents. After Einstein’s work, they knew better.”

“It’s frames again, ain’t it?”

“Of course, Vinnie. A‘s frame is almost certainly moving relative to B‘s frame. Motion puts the Lorentz relativity factor into the game, making each astronomer’s clock run faster than the other’s. Worse, each astronomer sees that the other’s yardsticks are too short.”

Jeremy gives me a confused look.

“Space compression goes along with time dilation, Jeremy. Professor Hanneken will explain it all when your class gets to that unit. Bottom line, things can happen simultaneously in Einstein’s Universe, but no‑one can agree on which things.”

“Wait, if every frame has its own time‑rate, how can two spaceships rendezvous for an operation?”

“Good question, Jeremy. Einstein had an answer but complications hide under the covers. He suggested that A start a timer when sending a light pulse to a mirror at B. A waits for the reflection. B starts a timer when they see A‘s pulse. A measures the pulse’s round‑trip time. Each creates a clock that advances one tick for half of the round-trip time. B sets their clock back by one tick. That done, they agree to meet some number of ticks later.”

“Hmm… That should work, but you said there are complications.”

“There are always complications. For instance, suppose B is slingshotting around a black hole so that pulse and reflection travel different pathlengths. Or suppose one frame is rotating edge‑on to the other. In practice the ships would re‑sync repeatedly while approaching the rendezvous point.”

Vinnie erupts. “HAW! Successive approximation again!”

“Indeed. If we could extend the method to more than two participants we’d have a true Universal Coordinated Time.”

“Don’t we have that, Mr Moire? The Big Bang happened 14 billion years ago. Couldn’t we measure time from that?”

“Sort of. Last I looked the number was 13.787 plus‑or‑minus 20 million years. Too much slop for an instantaneous fleet‑level rendezvous like the final battle scene in StarTrek:Picard. But you’ve brought up an interesting question for a Crazy Theories seminar. One of Cosmology’s deepest unsolved questions is, ‘How does inertia work?’ Do you remember Newton’s First Law?”

<closes eyes> “In an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.“

“Right. In other words, every object resists change to its current steady motion along a geodesic. Why is that? There’s no coherent, well‑founded, well‑tested theory. Einstein liked Mach’s Principle, which says inertia exists because every object is attracted through space to all the mass in the Universe. Suppose there’s a Mach’s Principle for Time, saying that objects squirt up the Time axis because they’re repelled by all the mass in the Universe.”

Vinnie hoots, “Bo-o-o-ohh-GUS!”

~ Rich Olcott

Cause, Effect And Time

On By rolcottIn Physics: Black Holes and Relativity, Uncategorized5 Comments

We’re still at Vinnie’s table by the door of Al’s coffee shop. “Long as we’re talking about black holes, Sy, I read in one of my astronomy magazines that an Event Horizon traps information the same way it traps light. I understand how gravity makes escape velocity for photons go beyond lightspeed, but how does that trap information?”

“Well, to start with, Al, you understand wrong. The whole idea of escape velocity applies to massive objects like rockets that feel the force of gravity. Going up they trade kinetic energy for potential energy; given enough kinetic energy they escape. Photons have zero mass — the only way gravity influences them is by bending the spacetime they fly through.”

“Does the bending also affect information or is that something else?”

Minkowski’s spacetime diagram…

“Fair question, but it’ll take some background to answer it. Good thing I’ve got Old Reliable and my graphics files along. Let’s start with this one. Vinnie’s seen a lot of spacetime graphs like this, Al, but I don’t think you have. Time runs upward, distance runs sideward, okay? Naming a specific time and location specifies an event, just like a calendar entry. Draw a line between two events; the slope is the speed you have to go to get from one to the other.”

“Just the distance, you’re not worrying about direction?”

“Good question. You’re thinking space is 3D and this picture shows only one space dimension. Einstein’s spacetime equations take account of all four dimensions mixing together, which is one reason they’re so hard to solve except in special cases. For where we’re going, distance will be enough, okay?”

“Not gonna argue.”

… compartmentalized by Einstein’s speed limit …

“Now we roll in Einstein’s speed limit. Relativity says that nothing can go faster than light. On a Minkowski diagram like this we draw the lightspeed slope at a 45″ angle. Any physical motion has a slope more vertical than that.”

“Huh?”

“See, Al, you’re going one second per second along time, right? If you’re not making much progress distance‑wise, you don’t do much on Sy’s sideways axis. You move mostly up.”

“Exactly, Vinnie. The bottom and top sections are called ‘timelike‘ because, well, they’re mostly like time.”

“Are the other two sections spacelike?”

“Absolutely. You can’t get from ‘Here & Now‘ to the ‘Too far to see‘ event without going faster than light. Einstein said that’s a no‑no. Suppose that event’s a nova, ‘Now‘ but far away. Astronomers will have to just wait until the nova’s light reaches them at ‘Here‘ but at a later ‘Now.’ Okay, Vinnie, here’s a graphic you haven’t seen yet.”

… and re-interpreted in terms of causality.

“Looks pretty much the same, except for that arrow. What’s cause and effect got to do with time?”

“I don’t want to get into the metaphysical weeds here. There’s a gazillion theories about time — the Universe is expanding and that drives time; entropy always increases and that drives time; time is an emergent property of the underlying structure of the Universe, whatever that means. From an atomic, molecular, mechanical physics point of view, time is the result of causes driving effects. Causes always come first. Your finger bleeds after you cut it, not before. Cause‑effect runs along the time axis. Einstein showed us that cause‑effect can’t travel any faster than lightspeed.”

“That’s a new one. How’d he figure that?”

“Objects move objects to make things happen. They can’t move faster than lightspeed because of the relativity factor.”

“What if the objects are already touching?”

“Your hand and that cup are both made of atoms and it’s really their electric fields that touch. Shifting fields are limited by lightspeed, too.”

“So you’re saying that cause-effect is timelike.”

“Got it in one. Einstein would say causality is not only timelike, but exactly along the time axis. That’s one big reason he was so uncomfortable about action at a distance — a cause ‘Here‘ having an effect ‘There‘ with zero time elapsed would be a horizontal line, pure spacelike, on Minkowski’s graph. Einstein invented the principle of entanglement as a counterexample, thinking it impossible. He’d probably be shocked and distressed to see that today we have experimental proof of entanglement.”

~~ Rich Olcott

Now And Then And There

On By rolcottIn Cosmology, James Webb Space Telescope, Physics: Light and Relativity, UncategorizedLeave a comment

Still at our table in Al’s otherwise empty coffee shop. We’re leading up to how Physics scrambled ‘Now‘ when a bell dings behind the counter. Al dashes over there. Meanwhile, Cathleen scribbles on a paper napkin with her colored pencils. She adds two red lines just as Al comes back with a plate of scones. “Here, Sy, if you’re going to talk Minkowski space this might be useful.”

“Hah, you’re right, Cathleen, this is perfect. Thanks, Al, I’ll have a strawberry one. Mmm, I love ’em fresh like this. OK, guys, take a look at Cathleen’s graphy artwork.”

“So? It’s the tile floor here.”

“Not even close, Mr Feder. Check the labels. The up‑and‑down label is ‘Time’ with later as higher. The diagram covers the period we’ve been sitting here. ‘Now‘ moves up, ‘Here’ goes side‑to‑side. ‘Table‘ and ‘Oven‘, different points in space, are two parallel lines. They’re lines because they both exist during this time period. They’re vertical because neither one moves from its relative spatial position. Okay?”

“Go on, Moire.”
  ”Makes sense to me, Sy.”

“Good. ‘Bell‘ marks an event, a specific point in spacetime. In this case it’s the moment when we here at the table heard the bell. I said ‘spacetime‘ because we’re treating space and time as a combined thing. Okay?”

“Go on, Moire.”
  ”Makes sense to me, Sy.”

“So then Al went to the oven and came back to the table. He traveled a distance, took some time to do that. Distance divided by time equals velocity. ‘Table‘ has zero velocity and its line is vertical. Al’s line would tilt down more if he went faster, okay?”

“Mmmm, got it, Sy.”
  ”Cute how you draw the come-back label backwards, lady. Go on, Moire.”

“I do my best, Mr Feder.”

“Fine, you’ve got the basic ideas. Now imagine all around us there’s graph paper like this — except there’s no paper and it’s a 4‑dimensional grid to account for motion in three spatial dimensions while time proceeds. Al left and returned to the same space point so his spacetime interval is just the time difference. If two events differ in time AND place there’s special arithmetic for calculating the interval.”

“So where’s that get us, Moire?”

“It got 18th and 19th Century Physics very far, indeed. Newton and everyone after him made great progress using math based on a nice stable rectangular space grid crossed with an orderly time line. Then Lorentz and Poincaré and Einstein came along.”

“Who’s Poincaré?”

“The foremost mathematician of nineteenth Century France. A mine safety engineer most days and a wide‑ranging thinker the rest of the time — did bleeding‑edge work in many branches of physics and math, even invented a few branches of his own. He put Lorentz’s relativity work on a firm mathematical footing, set the spacetime and gravity stage for Minkowsky and Einstein. All that and a long list of academic and governmental appointments but somehow he found the time to have four kids.”

Simultaneity Animation by “Acdx”
licensed under Creative Commons Attribution-Share Alike 4.0 International.

“A ball of fire, huh? So what’d he do to Newton’s jungle gym?”

“Turned its steel rod framework into jello. Remember how Cathleen’s Minkowski diagram connected slope with velocity? Einstein showed how Lorentz’s relativity factor sets a speed limit for our Universe. On the diagram, that’d be a minimum slope. Going vertical is okay, that’s standing still in space. Going horizontal isn’t, because that’d be instantaneous travel. This animation tells the ‘Now‘ story better than words can.”

“Whah?”
  ”Whah?”

“We’re looking down on three space travelers and three events. Speeds below lightspeed are within the gray hourglass shape. The white line perpendicular to each traveler’s time line is their personal ‘Now‘. The travelers go at different velocities relative to us so their slopes and ‘Now‘ lines are different. From our point of view, time goes straight up. One traveler is sitting still relative to us so its timeline is marked ‘v=0‘ and parallels ours. We and the v=0 traveler see events A, B and C happening simultaneously. The other travelers don’t agree. ‘Simultaneous‘ is an illusion.”

~~ Rich Olcott

Hyperbolic plane image by Murdock Grewar,
licensed under Creative Commons Attribution-Share Alike 4.0 International.

Speed Limit

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Wait, Sy, there’s something funny about that Lorentz factor. I’m riding my satellite and you’re in your spaceship to Mars and we compare notes and get different times and lengths and masses and all so we have to use the Lorentz factor to correct numbers between us. Which velocity do we use, yours or mine?”

“Good question, Vinnie. We use the difference between our two frames. We can subtract either velocity from the other one and replace v with that number. Strictly speaking, we’d subtract velocity components perpendicular to the vector between us. If I were to try to land on your satellite I’d have to expend fuel and energy to change my frame’s velocity to yours. When we matched frames the velocity difference would be zero, the Lorentz factor would be 1.0 and I’d see your solar array as a perfect 10×10‑meter square. Our clocks would tick in sync, too.”

“OK, now there’s another thing. That Lorentz formula compares our subtracted speeds to lightspeed c. What do we subtract to get c?”

“Deep question. That’s one of Einstein’s big insights. Suppose from my Mars‑bound spaceship I send out one light pulse toward Mars and another one in the reverse direction, and you’re watching from your satellite. No matter how fast my ship is traveling, Einstein said that you’d see both pulses, forward and backward, traveling at the same speed, c.”

“Wait, shouldn’t that be that your speed gets added to one pulse and subtracted from the other one?”

“Ejected mass works that way, but light has no mass. It measures its speed relative to space itself. What you subtract from c is zero. Everywhere.”

“OK, that’s deep. <pause> But another ‘nother thing—”

“For a guy who doesn’t like equations, you’re really getting into this one.”

“Yeah, as I get up to speed it grows on me. HAW!”

“Nice one, you got me. What’s the ‘nother thing?”

“I remembered how velocity is speed and direction but we’ve been mixing them together. If my satellite’s headed east and your spaceship’s headed west, one of us is minus to the other, right? We’re gonna figure opposite v‑numbers. How’s that work out?”

“You’re right. Makes no difference to the Lorentz factor because the square of a negative difference is the same as the square of its positive twin. You bring up an important point, though — the factor applies to both of us. From my frame, your clock is running slow. From your frame, mine’s the slow one. Einstein’s logic says we’re both right.”

“So we both show the same wrong time, no problem.”

“Nope, you see my clock running slow relative to your clock. I see exactly the reverse. But it gets worse. How about getting your pizza before you order it?”

“Eddie’s good, he ain’t that good. How do you propose to make that happen?”

“Well, I don’t, but follow me here. <working numbers on Old Reliable> Suppose we’re both in spaceships. I’m loafing along at 0.75c relative to Eddie’s pizza place on Earth and your ship is doing 3c. Also, suppose that we can transmit messages and mass much faster than lightspeed.”

“Like those Star Trek transporters and subspace radios.”

“Right. OK, at noon on my personal clock you tell me you’ve ordered pizza so I get one, too. Eddie slaps both our pizzas into his transporter 10 minutes later. The math works out that according to my clock you get your pizza 8.9 minutes before you put in your order. You like that?”

“Gimme a sec … nah, I don’t think so. If I read that formula right with v1 being you and v2 being me, if you run that formula for what I’d see with my velocity on the bottom, that’s a square root of a minus which can’t be right.”

“Yup, the calculation gives an imaginary number, 4.4i minutes, whatever that means. So between us we have two results that are just nonsense — I see effect before cause and you see a ridiculous time. To avoid that sort of thing, Einstein set his speed limit for light, gravity and information.”

“I’m willing to keep under it if you are.”

“Deal.”

~~ Rich Olcott

The Relativity Factor

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Sy, it’s nice that Einstein agreed with Rayleigh’s wave theory stuff but why’d you even drag him in? I thought the faster‑than‑light thing was settled.”

“Vinnie, faster‑than‑light wasn’t even an issue until Einstein came along. Science had known lightspeed was fast but not infinite since Rømer measured it in Newton’s day. ‘Pretty fast,’ they said, but Newtonian mechanics is perfectly happy with any speed you like. Then along came Einstein.”

“Speed cop, was he?”

“Funny, Vinnie. No, Einstein showed that the Universe enforces the lightspeed limit. It’s central to how the Universe works. Come to think of it, the crucial equation had been around for two decades, but it took Einstein to recognize its significance.”

“Ah, geez, equations again.”

“Just this one and it’s simple. It’s all about comparing v for velocity which is how fast something’s going, to c the speed of light. Nothing mystical about the arithmetic — if you’re going half the speed of light, the factor works out to 1.16. Ninety‑nine percent of c gives you 7.09. Tack on another 9 and you’re up to 22.37 and so on.”

“You got those numbers memorized?”

“Mm-hm, they come in handy sometimes.”

“Handy how? What earthly use is it? Nothing around here goes near that fast.”

“Do you like your GPS? It’d be useless if the Lorentz factor weren’t included in the calculations. The satellites that send us their sync signals have an orbit about 84 000 kilometers wide. They run that circle once a sidereal day, just shy of 86 400 seconds. That works out to 3 kilometers per second and a Lorentz factor of 1.000 005.”

“Yeah, so? That’s pretty close to 1.0.”

“It’s off by 5 parts per million. Five parts per million of Earth’s 25 000-mile circumference is an eighth of a mile. Would you be happy if your GPS directed you to somewhere a block away from your address?”

“Depends on why I’m going there, but I get your point. So where else does this factor come into play?”

“Practically anywhere that involves a precision measurement of length or duration. It’s at the core of Einstein’s Special Relativity work. He thought about observing a distant moving object. It’s carrying a clock and a ruler pointed along the direction of motion. The observer would see ticks of the clock get further apart by the Lorentz factor, that’s time dilation. Meanwhile, they’d see the ruler shrink by the factor’s inverse, that’s space compression.”

“What’s this ‘distant observer‘ business?”

“It’s less to do with distance than with inertial frames. If you’re riding one inertial frame with a GPS satellite, you and your clock stay nicely synchronized with the satellite’s signals. You’d measure its 1×1‑meter solar array as a perfect square. Suppose I’m riding a spaceship that’s coasting to Mars. I measure everything relative to my own inertial frame which is different from yours. With my telescope I’d measure your satellite’s solar array as a rectangle, not a square. The side perpendicular to the satellite’s orbit would register the expected 1 meter high, but the side pointing along the orbit would be shorter, 1 meter divided by the Lorentz factor for our velocity difference. Also, our clocks would drift apart by that Lorentz factor.”

“Wait, Sy, there’s something funny about that equation.”

“Oh? What’s funny?”

“What if somebody’s speed gets to c? That’d make the bottom part zero. They didn’t let us do that in school.”

“And they shouldn’t — the answer is infinity. Einstein spotted the same issue but to him it was a feature, not a bug. Take mass, for instance. When they meet Einstein’s famous E=mc² equation most people think of the nuclear energy coming from a stationary lump of uranium. Newton’s F=ma defined mass in terms of a body’s inertia — the greater the mass, the more force needed to achieve a certain amount of acceleration. Einstein recognized that his equation’s ‘E‘ should include energy of motion, the ½mv² kind. He had to adjust ‘m‘ to keep F=ma working properly. The adjustment was to replace inertial mass with ‘relativistic mass,’ calculated as inertial mass times the Lorentz factor. It’d take infinite force to accelerate any relativistic mass up to c. That’s why lightspeed’s the speed limit.”

~~ Rich Olcott