Tag: Momentum

It’s All About The Coupling

On By rolcottIn UncategorizedLeave a comment

The game‘s over but there’s still pizza on the table so Eddie picks up the conversation. “So if gadolinoleum has even more unpaired electrons than iron, how come it’s not ferromagnetic like iron is?”

Vinnie’s tidying up the chips he just won. “I bet I know part of it, Eddie. Sy and me, we talked about magnetic domains some years ago. If I remember right, each iron atom in a chunk is a tiny little magnet, which I guess is the fault of its five unpaired electrons, but usually the atom magnets are pointing in all different directions so they all average out and the whole chunk doesn’t have a field. If you stroke the chunk with a magnet, that collects the little magnets into domains and the whole thing gets magnetic. How come gadomonium” <winks at Eddie, Eddie winks back> “doesn’t play the domain game, Susan?”

“It’s gadolinium, boys, please. As to the why, part’s at the atom level and part’s higher up. My lab neighbor Tammy schooled me on rare earth magnetism just last week. She does high‑temperature solid state chemistry with lanthanide‑containing materials. Anyway, she says it’s all about coupling.”

“I hope she told you more than that.”

The angular portion of the lowest-energy spherical harmonic modes
Credit: Inigo.quilez, under CCA SA 3.0 license

“She did. Say you’ve got a single gadolinium atom floating in space. Its environment is spherically symmetrical, no special direction to organize the wave‑orbitals hosting unpaired charges. Now turn on a magnetic field to tell the atom which way is up, call that the z‑axis. The atom’s wave‑orbital with zero angular momentum orients along z. Six more wave‑orbitals with non‑zero angular momentum spin one way or the other at various angles to the z‑axis. Those charges in motion build the atom’s personal magnetic field.”

“But we’re on Earth, not in space.”

“Bear with me. First, as a chemist I must say that most of the transition and lanthanide elements happily lose two electrons so in general we’re dealing with ions. Before you ask, Vinnie, that goes even for metals where the ions float in an electron sea. When Tammy said ‘coupling’ she was talking about how strongly one ion feels the neighboring fields. Iron and other ferromagnetic materials have a strong coupling, much stronger than the paramagnetics do.”

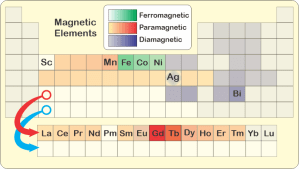
“Why’s the ferro- coupling so much stronger?”

“Two effects. You can read both of them right off the Periodic Table. Physical size, for one. Each row down in the table represents one electronic shell which takes up space. The atom or ion in any row is bigger than the ones above it. Yes, the heavy elements have more nuclear charge to pull electronic charge close, but shielding from their completed lower shells lets the outer charge cloud expand. Tammy told me that gadolinium’s ions are about 20% wider than iron’s.”

“Makes sense — you make the ions get further apart, they won’t connect so good. What’s the other effect?”

“It’s about how each orbital distributes its charge. There are tradeoffs between shell number, angular momentum and distance from the nucleus. Unpaired charge concentration in gadolinium’s high‑momentum 4f‑orbitals on the average stays inside of all its 3‑shell waves. The outermost charge shelters the unpaired waves inside it. That weakens magnetic coupling with unpaired charge in neighboring ions. Bottom line — gadolinium and its cousins are paramagnetic because they’re bigger and less sensitive than ferromagnetic iron is.”

“Then how come rare earth supermagnets the Chinese make are better than the cheapie ironic kinds we can make here?”

“The key is getting the right atoms into the right places in a crystalline solid. Neodymium magnets, for instance, have clusters of iron atoms around each lanthanide. The cluster arrangement aligns everyone’s z‑axes letting the unpaired charges gang up big‑time. You find materials like that mostly by luck and persistence. Tammy’s best samples are multi‑element oxides that arrange themselves in planar layers. Pick a component just 1% off the ideal size or cook your mixture with the wrong temperature sequence and the structure has completely different properties. Chinese scientists worked decades to perfect their recipes. USA chose to starve research in that area.”

~ Rich Olcott

Flipping An Edge Case

On By rolcottIn Chemistry, Physics: Quantum Mechanics, UncategorizedLeave a comment

“Why’s the Ag box look weird in your chart, Susan?”

“That’s silver, Eddie. It’s an edge case. The pure metal’s diamagnetic. If you alloy silver with even a small amount of iron, the mixture is paramagnetic. How that works isn’t my field. Sy, it’s your turn to bet and explain.”

I match Eddie’s bet (the hand’s not over). “It’s magnetism and angular momentum and how atoms work, and there are parts I can’t explain. Even Feynman couldn’t explain some of it. Vinnie, what do you remember about electromagnetic waves?”

“Electric part pushes electrons up and down, magnetic part twists ’em sideways.”

“Good enough, but as Newton said, action begets reaction. Two centuries ago, Ørsted discovered that electrons moving along a wire create a magnetic field. Moving charges always do that. The effect doesn’t even depend on wires — auroras, fusion reactor and solar plasmas display all sorts of magnetic phenomena.”

“You said it’s about how atoms work.”

“Yes, I did. Atoms don’t follow Newton’s rules because electrons aren’t bouncing balls like those school‑book pictures show. An electron’s only a particle when it hits something and stops; otherwise it’s a wave. The moving wave carries charge so it generates a magnetic field proportional to the wave’s momentum. With me?”

“Keep going.”

“That picture’s fine for a wave traveling through space, but in an atom all the charge waves circle the nucleus. Linear momentum in open space becomes angular momentum around the core. If every wave in an atom went in the same direction it’d look like an electron donut generating a good strong dipolar magnetic field coming up through the hole.”

“You said ‘if’.”

“Yes, because they don’t do that. I’m way over‑simplifying here but you can think of the waves pairing up, two single‑electron waves going in opposite directions.”

“If they do that, the magnetism cancels.”

“Mm‑hm. Paired‑up configurations are almost always the energy‑preferred ones. An external magnetic field has trouble penetrating those structures. They push the field away so we classify them as diamagnetic. The gray elements in Susan’s chart are almost exclusively in paired‑up configurations, whether as pure elements or in compounds.”

“Okay, so what about all those paramagnetic elements?”

The angular portion of the lowest-energy spherical harmonic modes
Credit: Inigo.quilez, under CCA SA 3.0 license

“Here’s where we get into atom structure. An atom’s electron cloud is described by spherical harmonic modes we call orbitals, with different energy levels and different amounts of angular momentum — more complex shapes have more momentum. Any orbital hosting an unpaired charge has uncanceled angular momentum. Two kinds of angular momentum, actually — orbital momentum and spin momentum.”

“Wait, how can a wave spin?”

“Hard to visualize, right? Experiments show that an electron carries a dipolar magnetic field just like a spinning charge nubbin would. That’s the part that Feynman couldn’t explain without math. A charge wave with spin and orbital angular momentum is charge in motion; it generates a magnetic field just like current through a wire does. The math makes good predictions but it’s not something that everyday experience prepares us for. Anyway, the green and yellow‑orange‑ish elements feature unpaired electrons in high‑momentum orbitals buried deep in the atom’s charge cloud.”

“So what?”

“So when an external magnetic field comes along, the atom’s unpaired electrons join the party. They orient their fields parallel to the external field, in effect allowing it to penetrate. That qualifies the atom as paramagnetic. More unpaired electrons means stronger interaction, which is why iron goes beyond paramagnetic to ferromagnetic.”

“How does iron have so many?”

“Iron’s halfway across its row of ten transition metals—”

“I know where you’re going with this, Sy. It’ll help to say that these elements tend to lose their outer electrons. Scandium over on the left ionizes to Sc3+ and has zero d‑electrons. Then you add one electron in a d orbital for each move to the right.”

“Thanks, Susan. Count ’em off, Vinnie. Five steps over to iron, five added d‑electrons, all unpaired. Gadolinium, down in the lanthanides, beats that with seven half‑filled f‑orbitals. That’s where the strength in rare earth magnets arises.”

“So unpaired electrons from iron flip alloyed silver paramagnetic?”

“Vinnie wins this pot.”

~ Rich Olcott

A Cosmological Horse Race

On By rolcottIn Astronomy: Multi-messenger, Cosmology, Physics: Einstein, Physics: Electromagnetism, UncategorizedLeave a comment

A crisp Fall day, perfect for a brisk walk around the park. I see why the geese are huddled at the center of the lake — Mr Feder, not their best friend, is on patrol again. Then he spots me. “Hey, Moire, I gotta question!”

“Of course you do, Mr Feder. What is it?”

“Some guy on TV said Einstein proved gravity goes at the speed of light and if the Sun suddenly went away it’d take eight minutes before we went flying off into space. Did Einstein really say that? Why’d he say that? Was the TV guy right? And what would us flying across space feel like?”

“I’ll say this, Mr Feder, you’re true to form. Let’s see… Einstein didn’t quite prove it, the TV fellow was right, and we’d notice being cold and in the dark well before we’d notice we’d left orbit. As to why, that’s a longer story. Walk along with me.”

“Okay, but not too fast. What’s not quite about Einstein’s proving?”

“Physicists like proofs that use dependable mathematical methods to get from experimentally-tested principles, like conservation of energy, to some result they can trust. We’ve been that way since Galileo used experiments to overturn Aristotle’s pure‑thought methodology. When Einstein linked gravity to light the linkage was more like poetry. Beautiful poetry, though.”

“What’s so beautiful about something like that?”

“All the rhymes, Mr Feder, all the rhymes. Both gravity and light get less intense with the square of the distance. Gravity and light have the same kinds of symmetries—”

“What the heck does that mean?”

“If an object or system has symmetry, you can execute certain operations on it yet make no apparent difference. Rotate a square by 90° and it looks just the same. Gravity and light both have spherical symmetry. At a given distance from a source, the field intensity’s the same no matter what direction you are from the source. Because of other symmetries they both obey conservation of momentum and conservation of energy. In the late 1890s researchers found Lorentz symmetry in Maxwell’s equations governing light’s behavior.”

“You’re gonna have to explain that Lorentz thing.”

“Lorentz symmetry has to do with phenomena an observer sees near an object when their speed relative to the object approaches some threshold. Einstein’s Special Relativity theory predicted that gravity would also have Lorentz symmetry. Observations showed he was right.”

“So they both do Lorentz stuff. That makes them the same?”

“Oh, no, completely different physics but they share the same underlying structure. Maxwell’s equations say that light’s threshold is lightspeed.”

“Gravity does lightspeed, too, I suppose.”

“There were arguments about that. Einstein said beauty demands that both use the same threshold. Other people said, ‘Prove it.’ The strongest argument in his favor at the time was rough, indirect, complicated, and had to do with fine details of Earth’s orbit around the Sun. Half a century later pulsar timing data gave us an improved measurement, still indirect and complicated. This one showed gravity’s threshold to be with 0.2% of lightspeed.”

“Anything direct like I could understand it?”

“How about a straight‑up horse race? In 2017, the LIGO facility picked up a gravitational signal that came in at the same time that optical and gamma ray observatories recorded pulses from the same source, a colliding pair of neutron stars in a galaxy 130 million lightyears away. A long track, right?”

“Waves, not horses, but how far apart were the signals?”

“Close enough that the measured speed of gravity is within 10–15 of the speed of light.”

“A photo-finish.”

“Nice pun, Mr Feder. We’re about 8½ light-minutes away from the Sun so we’re also 8½ gravity-minutes from the Sun. As the TV announcer said, if the Sun were to suddenly dematerialize then Earth would lose the Sun’s orbital attraction 8½ minutes later. We as individuals wouldn’t go floating off into space, though. Earth’s gravity would still hold us close as the whole darkened, cooling planet leaves orbit and heads outward.”

“I like it better staying close to home.”

~ Rich Olcott

A No-Charge Transaction

On By rolcottIn Cosmology, Crazy Theories, Physics: Light and Relativity, UncategorizedLeave a comment

“I ain’t done yet, Sy. I got another reason for Dark Matter being made of faster‑then‑light tachyons.”

“I’m still listening, Vinnie.”

“Dark Matter gotta be electrically neutral, right, otherwise it’d do stuff with light and that doesn’t happen. I say tachyons gotta be neutral.”

“Why so?”

“Stands to reason. Suppose tachyons started off as charged particles. The electric force pushes and pulls on charges hugely stronger than gravity pulls—”

“1036 times stronger at any given distance.”

“Yeah, so right off the bat charged tachyons either pair up real quick or they fly away from the slower‑than‑light bradyon neighborhood leaving only neutral tachyons behind for us bradyon slowpokes to look at.”

“But we’ve got un‑neutral bradyon matter all around us — electrons trapped in Earth’s Van Allen Belt and Jupiter’s radiation belts, for example, and positive and negative plasma ions in the solar wind. Couldn’t your neutral tachyons get ionized?”

“Probably not much. Remember, tachyon particles whiz past each other too fast to collect into a star and do fusion stuff so there’s nobody to generate tachyonic super‑high‑energy radiation that makes tachyon ions. No ionized winds either. If a neutral tachyon collides with even a high-energy bradyon, the tachyon carries so much kinetic energy that the bradyon takes the damage rather than ionize the tachyon. Dark Matter and neutral tachyons both don’t do electromagnetic stuff so Dark Matter’s made of tachyons.”

“Ingenious, but you missed something way back in your initial assumptions.”

“Which assumption? Show me.”

“You assumed that tachyon mass works the same way that bradyon mass does. The math says it doesn’t.” <grabbing scratch paper for scribbling> “Whoa, don’t panic, just two simple equations. The first relates an object’s total energy E to its rest mass m and its momentum p and lightspeed c.”

E² = (mc²)² + (pc)²

“I recognize the mc² part, that’s from Einstein’s Equation, but what’s the second piece and why square everything again?”

“The keyword is rest mass.”

“Geez, it’s frames again?”

“Mm‑hm. The (mc²)² term is about mass‑energy strictly within the object’s own inertial frame where its momentum is zero. Einstein’s famous E=mc² covers that special case. The (pc)² term is about the object’s kinetic energy relative to some other‑frame observer with relative momentum p. When kinetic energy is comparable to rest‑mass energy you’re in relativity territory and can’t just add the two together. The sum‑of‑squares form makes the arithmetic work when two observers compare notes. Can I go on?”

“I’m still waitin’ to hear about tachyons.”

“Almost there. If we start with that equation, expand momentum as mass times velocity and re‑arrange a little, you get this formula

E = mc² / √(1 – v²/c²)

The numerator is rest‑mass energy. The v²/c² measures relative kinetic energy. The Lorentz factor down in the denominator accounts for that. See, when velocity is zero the factor is 1.0 and you’ve got Einstein’s special case.”

“Give me a minute. … Okay. But when the velocity gets up to lightspeed the E number gets weird.”

“Which is why c is the upper threshold for bradyons. As the velocity relative to an observer approaches c, the Lorentz factor approaches zero, the fraction goes to infinity and so does the object’s energy that the observer measures.”

“Okay, here’s where the tachyons come in ’cause their v is bigger than c. … Wait, now the equation’s got the square root of a negative number. You can’t do that! What does that even mean?”

“It’s legal, when you’re careful, but interpretation gets tricky. A tachyon’s Lorentz factor contains √(–1) which makes it an imaginary number. However, we know that the calculated energy has to be a real number. That can only be true if the tachyon’s mass is also an imaginary number, because i/i=1.”

“What makes imaginary energy worse than imaginary mass?”

“Because energy’s always conserved. Real energy stays that way. Imaginary mass makes no sense in Newton’s physics but in quantum theory imaginary mass is simply unstable like a pencil balanced on its point. The least little jiggle and the tachyon shatters into real particles with real kinetic energy to burn. Tachyons disintegrating may have powered the Universe’s cosmic inflation right after the Big Bang — but they’re all gone now.”

“Another lovely theory shot down.”

~ Rich Olcott

Why A Disk?

On By rolcottIn Astronomy: Stellar Science, Cosmology, UncategorizedLeave a comment

Late Summer is quiet time on campus and in my office. Too quiet. I head over to Cal’s coffee shop in search of company. “Morning, Cal.”

“Morning, Sy. Sure am glad to see you. There’s no‑one else around.”

“So I see. No scones in the rack?”

“Not enough traffic yet to justify firing up the oven on such a hot day. How about a biscotti instead?”

“If it’s only the one it’s a biscotto. Pizza Eddie’s very firm on that. Yeah, I’ll have one.”

“Always learning. By the way, a photo spread in one of my astronomy magazines got me thinking. How come there’s so much flat out there?”

“Huh? I know you’re not one of those flat‑Earthers.”

“Not the planets, I mean the way their orbits go all in the same plane. Same for most of the asteroids and the Kuiper belt, even. Our Milky Way galaxy’s basically flat, too, and so are a lot of the others. Black hole accretion disks are flat. You’d think if some baby star or galaxy was attracting stuff from everywhere to grow itself, the incoming would make a big globe. But it’s not, we get flatness. How come?”

“Bad aim and angular momentum.”

“What’s aim got to do with it?”

“Suppose there’s only two objects in the Universe and they’re closing in on each other. If they’re aimed dead‑center to each other, what happens?”

“CaaaRUNCH!!!”

“Right. Now what if the aim’s off so they don’t quite touch?”

“Oh, I know that one … it’ll come to me … yeah, Roche’s limit, it was in an article a few months ago. Whichever’s less dense will break up and all the pieces go like Saturn’s rings. Which are also flat, by the way.”

“In orbit around the survivor, mm‑hm. The pieces can’t fall straight down because they still have angular momentum.”

“I know about momentum like when you crash a car if you go too fast for your brakes. Heavier car or faster speed, you get a worse crash. How does angle fit into that — bigger angle, more angular momentum?”

“Not quite. In general, momentum is mass multiplied by speed. It’s a measure of the force required to stop something or at least slow it down. You’ve described linear momentum, where ‘speed’ is straight‑line distance per time. If you’re moving along a curve, ‘speed’ is arc‑length per time.”

“Arc‑length?”

“Distance around part of a circle. Arc‑length is angle in radians, multiplied by the circle’s radius. If you zip halfway around a big circle in the same time it took me to go halfway around a small circle, you’ve got more angular momentum than I do and it’d take more force to stop you. Make sense?”

“What if it’s not a circle? The planet orbits are all ellipses.”

“It’s still arc‑length except that you need calculus to figure it. That’s why Newton and Leibniz invented their methods. A falling something that misses a gravity center keeps falling but on an orbit. Whatever momentum it has acts as angular momentum relative to that center. There’s no falling any further in without banging into something else coming the other way and each object canceling the other’s momentum.”

“Or burning fuel if it’s a spaceship.”

“… Right. … So anyway, suppose you’ve got a star or something initially surrounded by a spherical cloud of space junk whirling around in all different orbits. What’s going to happen?”

“Lots of banging and momentum canceling until everything’s swirling more‑or‑less in the same direction and closer in than at come‑together time. But it’s still a ball.”

“Gravity’s not done. Think about northern debris. It’s attracted to the center, but it’s also attracted to the southern debris and vice-versa. They’ll meet midway and build a disk. The ball‑to‑disk collapse isn’t even opposed by angular momentum. Material at high latitudes, north and south, can lose gravitational potential energy by dropping straight in toward the equator and still be at the orbitally correct distance from the axis of rotation.”

“That’d work for stuff collecting around a planet, wouldn’t it?”

“It’d even work for stuff collecting around nothing, just a clump in a random density field. That may be how stars are born. Collapsing’s the hard part.”

~ Rich Olcott

The Beaming Beacon

On By rolcottIn Astronomy: Techniques, Physics: Black Holes and Relativity, Physics: Light and Relativity, UncategorizedLeave a comment

“So, Vinnie, that first article’s bogus. Blobs in M87’s supermassive black hole’s jet don’t travel faster than light. Your second article — is it also about M87*?”

M87* image – Credit EHT Collaboration

“Yeah, Cathleen. It’s got this picture which a while ago Sy explained looks like a wrung‑out towel because that’s the way the thing’s magnetic field forces electrons to line up and give off polarized light.”

“As always, Vinnie, your memory impresses.”

“Thanks, I work at it. Anyhow, this one‑paragraph article says they figured out from the picture that everything’s spinning around as fast as it’s possible to spin. How fast is that, and how’d they get the spin speed if they only used one frequency so redshift/blueshift doesn’t apply?”

Cathleen’s been poking at her tablet. “HAH! Found the real paper behind your pop‑sci article, Vinnie. Give me a minute…” <pause, with mumbling> “Wow, not much there in the disk. They estimate even at the crowded innermost orbit, they call it ISCO, the density’s about 10-14 kg/m3 which would be one nanopascal of pressure. Most labs consider that ultrahigh vacuum. They get angular momentum from something called ‘Doppler beaming’, which I’m not familiar with.” <passes tablet to me> “Your turn, Sy.”

“ISCO’s the Innermost Stable Circular Orbit. ISCO’s radius depends on the black hole’s mass and spin.” <pause, with mumbling> “Doppler beaming’s a velocity‑dependent brightness shift from outbound to inbound sides of ISCO. They connected brightness range within the images to ISCO velocity, multiplied that by ISCO radius and the black hole’s mass to get the disk’s angular momentum, J. The lightspeed rotation angular momentum Jmax comes from theory. The paper puts a number to M87*’s J/Jmax.“

“My article says it’s near 100%.”

“That’s not what the paper says, Vinnie. ‘…our value of 0.8 would appear to be a lower limit,’ in other words, something above 80% but definitely not 100%. Like I said, pop‑sci journalism. So what’s Doppler beaming, Sy?”

“Classical Doppler shifts happen when a wave source moves relative to us. Motion toward us crams successive wave peaks into decreasing distance. Motion away increases wavelength. The same principle applies to light waves, sound waves, even ocean waves.”

“Blueshifting.”

“Mm‑hm. By contrast, beaming is about how a source’s motion affects the photon count we receive per second. Imagine a beacon steadily sending us photons as it whips at near‑lightspeed around M87*. When the beacon screams towards us its motion crams more photons into one of our seconds than when it dashes away.”

“More blueshifting.”

“Not quite. Photon‑count compression sort‑of resembles the blueshifting process but wavelength isn’t relevant. It combines with the other part of beaming, Special Relativity space compression, which concentrates a moving beacon’s photons in the direction of motion. It’s like focusing a fancy flashlight, narrowing the beam to concentrate it. The faster the beacon travels in our direction, the greater proportion of its photons are sent towards us.”

Vinnie looks up and to the left. “If ISCO’s going near lightspeed, won’t the disk’s inertia drag on the black hole?”

“Sure, within limits. M87* and Sagittarius-A* both have magnetic fields; most black holes probably do. Accretion disk plasma must be frozen into the field. The whole structure would rotate like a spongy wheel with a fuzzy boundary. The lightspeed limit could cut in at the wheel’s rim, much farther out than the Event Horizon’s sphere.”

Count on Vinnie to jump on vagueness. “Spongy? Fuzzy?”

“Because nothing about a black hole’s extended architecture is rigid. It’s a messy mix of gravitational, electric and magnetic fields, all randomly agitated by transients from inbound chunks of matter and feeding outbursts from inside ISCO. The disk’s outer boundary is the raggedy region where the forces finally give way as centrifugal force works to fling particles out into the Universe. I don’t know how to calculate where the boundary is, but this image suggests it’s out about 10 times the Horizon’s radius. The question is, how does the boundary’s speed limit affect spin?” <tapping rapidly on Old Reliable’s screen>

“And the answer is…?”

“Disk particles driven close to lightspeed do push back. They lightly scramble those mushy fields but much too feebly to slow the central spin.”

~ Rich Olcott

Not Even A Sneeze in A Hurricane

On By rolcottIn General: Fun Stuff, Physics: Newton and Gravity, Space Travel, UncategorizedLeave a comment

Quite a commotion at the lakeshore this morning. I walk over to see what’s going on. Not surprised at who’s involved. “Come away from there, Mr Feder, you’re too close to their goslings.” Doesn’t work, of course, so I resort to stronger measures. “Hey, Mr Feder, any questions for me?”

That did the trick. “Hey, yeah, Moire, I got one. There’s this big problem with atomic power ’cause there’s leftovers when the fuel’s all used up and nobody wants it buried their back yard and I unnerstand that. How about we just load all that stuff into one of Musk’s Starships and send it off to burn up in the Sun? Or would that make the Sun blow up?”

“Second part first. Do you sneeze?”

“What kinda question is that? Of course I sneeze. Everyone sneezes.”

“Ever been in a hurricane?”

“Oohyeah. Sandy, back in 2012. Did a number on my place in Fort Lee. Took out my back fence, part of the roof, branches down all over the place—”

“Did you sneeze during the storm?”

“Who remembers that sort of thing?”

“If you had, would it have made any difference to how the winds blew?”

“Nah, penny‑ante compared to what else was going on. Besides, the storm eye went a couple hundred miles west of us.”

“Well, there you go. The Sun’s surface is covered by about a million granules, each about the size of Texas, and each releasing about 400 exawatts—”.

“Exawha?”

“Exawatt. One watt is one joule of energy per second. Exa– means 1018. So just one of those granules releases 400×1018 joules of energy per second. By my numbers that’s about 2300 times the total energy that Earth gets from the Sun. There’s a million more granules like that. Still think one of our rockets would make much difference with all that going on?”

“No difference anybody’d notice. But that just proves it’d be safe to send our nuclear trash straight to the Sun.”

“Safe, yes, but not practical.”

“When someone says ‘practical’ they’re about to do numbers, right?”

“Indeed. How much nuclear waste do you propose to ship to the Sun?”

“I dunno. How much we got?”

“I saw a 2022 estimate from the International Atomic Energy Agency that our world‑wide accumulation so far is over 265 000 tonnes, mostly spent fuel. Our heaviest heavy‑lift vehicle is the SpaceX Starship. Maximum announced payload to low‑Earth orbit is 400 tonnes for a one‑way trip. You ready to finance 662 launches?”

“Not right now, I’m a little short ’til next payday. How about we just launch the really dangerous stuff, like plutonium?”

“Much easier rocket‑wise, much harder economics‑wise.”

“Why do you say that?”

“Because most of the world’s nuclear power plants depend on MOX fuel, a mixture of plutonium and uranium oxides. Take away all the plutonium, you mess up a significant chunk of our carbon‑free‑mostly electricity production. But I haven’t gotten to the really bad news yet.”

“I’m always good for bad news. Give.”

“Even with the best of intentions, it’s an expensive challenge to shoot a rocket straight from Earth into the Sun.”

“Huh? It’d go down the gravity well just like dropping a ball.”

“Nope, not like dropping a ball. More like flinging it off to the side with a badly‑aimed trebuchet. Guess how fast the Earth moves around the Sun.”

“Dunno. I heard it’s a thousand miles an hour at the Equator.”

“That’s the planet’s rotation on its own axis. My question was how fast we go taking a year to do an orbit around the Sun. I’ll spare you the arithmetic — the planet speeds eastward at 30 kilometers per second. Any rocket taking off from Earth starts with that vector, and it’s at right angles to the Earth‑Sun line. You can’t hit the Sun without shedding all that lateral momentum. If you keep it, the rules of orbital mechanics force the ship to go faster and faster sideways as it drops down the well — you flat‑out miss the Sun. By the way, LEO delta‑v for SpaceX’s most advanced Starship is about 7 km/s, less than a fifth of the minimum necessary for an Earth‑to‑Sun lift.”

~ Rich Olcott

A Play Beyond The Play

On By rolcottIn Cosmology, Gravitational astronomy, Uncategorized, Vera RubinLeave a comment

Vinnie takes a long thoughtful look at the image that had dashed his beautiful six‑universe idea. “Wait, Sy. I don’t like this picture”

“Because it messes up your invention?”

“No, because how can they know what that halo looks like? I mean, the whole thing with dark matter is that we can’t see it.”

“You’re right about that. Dark matter’s so transparent that even with five times more mass than normal matter, it doesn’t block CMB photons coming from 13.8 billion lightyears away. That still boggles my brain every once in a while. But dark matter’s gravitational effects — those we can see.”

“Yeah, I remember a long time ago we talked about Fritz Zwicky and Vera Rubin and how they told people about galaxies held together by too much gravity but nobody believed them.”

“Well, they did, after a while—”

“A long while, like a long while since those talks. Remind me what ‘too much gravity’ was about.”

“It was about conflicts between their observations and the prevailing theoretical models. Everyone thought that galaxies and galaxy clusters should operate pretty much like planetary orbits — your speed increases the closer you are to the center, up to Einstein’s speed limit. Newton’s Laws of Motion predict how fast you should move if you’re at a certain distance from a body with a certain mass. If you’re moving faster than that, you fly away.”

“Yeah, escape velocity. So the galaxies in Zwicky’s cluster didn’t follow Newton’s Laws?”

“They didn’t seem to. Galaxies that should have escaped were still in there. The only way he could explain the stability was to suppose the galaxies are only a small fraction of the cluster’s mass. Extra gravity from the extra mass must bind things together. Forty years later Rubin’s improved technology revealed that stars within galaxies had the same anomalous motion.”

“I’m guessing the ‘faster near the center’ rule didn’t hold, or else you wouldn’t be telling this story. Spun like a wheel, I bet.”

“When a wheel spins, every part of it rotates at the same angular speed, the same number of degrees per second, right?”

“Ahh, the bigger my circle the higher my airspeed so the rule would be ‘faster farther out’.”

“That’s the wheel rule, right, but Rubin’s data showed that stars within galaxies don’t obey that one either. She measured lots of stars in Andromeda and other galaxies. Their linear speeds, kilometers per second, are nearly identical from near the center all the way out. Even dust and gas clouds beyond the galactic starry edges also fit the ‘same linear speed everywhere’ rule. You’d lose the bet.”

“That just doesn’t feel right. How can just gravity make that happen?”

“It can if the right amount of dark matter’s distributed in the right‑shaped smeared‑out hollowed‑out spherical halo. The halo’s radial density profile looks about like this. Of course, profiles for different galaxies differ in spread‑outness and other details, but the models are pretty consistent.”

“Wait, if dark matter only does gravity like you said, why’s that hole in the middle? Why doesn’t everything just fall inward?”

“Dark matter has mass so it also has inertia, momentum and angular momentum, just as normal matter does. Suppose some of the dark matter has collected gravitationally into a blob and the blob is moving slower than escape velocity. If it’s flying straight at the center of gravity it’ll get there and stay there, more or less. But if the blob’s aimed in any other direction, it has angular momentum relative to the center. Momentum’s conserved for dark matter, too. The blob eventually goes into orbit and winds up as part of the shell.”

“Does Zwicky’s galaxy cluster have a halo, too?”

“Not in the same way. Each galaxy probably has its own halo but the galaxies are far apart relative to their size. The theoreticians have burned huge amounts of computer time simulating the chaos inside large ensembles of gravity‑driven blobs. I just read one paper about a 4‑billion‑particle calculation and mind you, a ‘particle’ in this study carried more than a million solar masses. Big halos host subhalos, with filaments of minihalos tying them together. What we can’t see is complicated, too.”

~ Rich Olcott

Deep Dive

On By rolcottIn Chemistry, Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Sy, I’m trying to get my head wrapped around how the potential‑kinetic energy thing connects with your enthalpy thing.”

“Alright, Vinnie, what’s your cut so far?”

“It has to do with scale. Big things, like us and planets, we can see things moving and so we know they got kinetic energy. If they’re not moving steady in a straight line we know they’re swapping kinetic energy, give and take, with some kind of potential energy, probably gravity or electromagnetic. Gravity pulls things into a circle unless angular momentum gets in the way. How’m I doing so far?”

“I’d tweak that a little, but nothing to argue with. Keep at it.”

“Yeah, I know the moving is relative to whether we’re in the same reference frame and all that. Beside the point, gimme a break. So anyway, down to the quantum level. Here you say heat makes the molecules waggle so that’s kinetic energy. What’s potential energy like down there?”

<grabs another paper napkin> “Here’s a quick sketch of the major patterns.”

“Hmm. You give up potential energy when you fall and gravity’s graph goes down from zero to more negative forever, I guess, so gravity’s always attracting.”

“Pretty much, but at this level we don’t have to bother with gravity at all. It’s about a factor of 1038 weaker than electric interactions. Molecular motions are dominated by electromagnetic fields. Some are from a molecule’s other internal components, some from whatever’s around that brandishes a charge. We’ve got two basic patterns. One of them, I’m labeling it ‘Waggle,’ works like a pendulum, sweeping up and down that U‑shape around some minimum position, high kinetic energy where the potential energy’s lowest and vice‑versa. You know how water’s H‑O‑H molecules have that the V‑shape?”

“Yeah, me you and Eddie talked about that once.”

“Mm‑hm. Well, the V‑shape gives that molecule three different ways to waggle. One’s like breathing, both sides out then both sides in. If the hydrogens move too far from the oxygen, that stretches their chemical bonds and increases their potential energy so they turn around and go back. If they get too close, same thing. Bond strength is about the depth of the U. The poor hydrogens just stretch in and out eternally, swinging up and down that symmetric curve.”

“Awww.”

“That’s a chemist’s picture. The physics picture is cloudier. In the quantum version, over here’s a trio of fuzzy quarks whirling around each other to make a proton. Over there’s a slightly different fuzzy trio pirouetting as a neutron. Sixteen of those roiling about make up the oxygen nucleus plus two more for the hydrogens plus all their electrons — imagine a swarm of gnats. On the average the oxygen cloud and the two hydrogen clouds configure near the minimum of that U‑shaped potential curve but there’s a lot of drifting that looks like symmetrical breathing.”

“What about the other two waggles?”

“I knew you’d ask. One’s like the two sides of a teeterboard, oscillating in and out asymmetrically. The other’s a twist, one side coming toward you and then the other side. Each waggle has its own distinct set of resistance forces that define its own version of waggle curve. Each kind interacts with different wavelengths of infrared light which is how we even know about them. Waggle’s official name is ‘harmonic oscillator.’ More complicated molecules have lots of them.”

“What’s that ‘bounce’ curve about?”

“Officially that’s a Lennard-Jones potential, the simplest version of a whole family of curves for modeling how molecules bounce off each other. Little or no interaction at large distances, serious repulson if two clouds get too close, and a little stickiness at some sweet-spot distance. If it weren’t for the stickiness, the Ideal Gas Law would work even better than it does. So has your head wrapped better?”

“Sorta. From what I’ve seen, enthalpy’s PV part doesn’t apply in quantum. The heat capacity part comes from your waggles which is kinetic energy even if it’s clouds moving. Coming the other way, quantum potential energy becomes enthalpy’s chemical part with breaking and making chemical bonds. Did I bridge the gap?”

“Mostly, if you insist on avoiding equations.”

~ Rich Olcott

Rumford’s Boring Story

On By rolcottIn Physics: Entropy and Thermodynamics, UncategorizedLeave a comment

“Okay, Mr Moire, my grandfather’s engineering handbook has Specific Heat tables because Specific Heat measures molecular wabbling. If he’s got them, though, why’s Enthalpy in the handbook, too?”

“Enthalpy’s not my favorite technical term, Jeremy. It’s wound up in a centuries‑old muddle. Nobody back then had a good, crisp notion of energy. Descartes, Leibniz, Newton and a host of German engineers and aristocratic French hobby physicists all recognized that something made motion happen but everyone had their own take on what that was and how to calculate its effects. They used a slew of terms like vis viva, ‘quantity of motion,’ ‘driving force,’ ‘quantity of work,’ a couple of different definitions of ‘momentum‘ — it was a mess. It didn’t help that a lot of the argument went on before Euler’s algebraic notations were widely adopted; technical arguments without math are cumbersome and can get vague and ambiguous. Lots of lovely theories but none of them worked all that well in the real world.”

“Isn’t that usually what happens? I always have problems in the labs.”

“You’re not alone. Centuries ago, Newton’s Laws of Motion and Gravity made good predictions for planets, not so good for artillery trajectories. Gunners always had to throw in correction factors because their missiles fell short. Massachusetts‑born Benjamin Thompson, himself an artilleryman, found part of the reason.”

“Should I know that name?”

“In later years he became Count Rumford. One of those people who get itchy if they’re not creating something. He was particularly interested in heat — how to trap it and how to make it go where you want.”

“Wait, he was an American but he was a Count? I thought that was illegal.”

“Oh, he left the States before they were the States. During the Revolution he organized a Royalist militia in New York and then lit out for Europe. The Bavarians made him a Count after he spent half‑a‑dozen years doing creative things like reorganizing their army, building public works and introducing potato farming. He concocted a nourishing soup for the poor and invented the soup line for serving it up. But all this time his mind was on a then‑central topic of Physics — what is heat?”

“That was the late 1700s? When everyone said heat was some sort of fluid they called ‘caloric‘?”

“Not everyone, and in fact there were competing theories about caloric — an early version of the particle‑versus‑wave controversy. For a while Rumford even supported the notion that ‘frigorific’ radiation transmitted cold the same way that caloric rays transmitted heat. Whatever, his important contributions were more practical and experimental than theoretical. His redesign of the common fireplace was such an improvement that it took first England and then Europe by storm. Long‑term, though, we remember him for a side observation that he didn’t think important enough to measure properly.”

“Something to do with heat, I’ll bet.”

“Of course. As a wave theory guy, Rumford stood firmly against the ‘caloric is a fluid‘ camp. ‘If heat is material,‘ he reasoned, ‘then a heat‑generating process must eventually run out of caloric.’ He challenged that notion by drilling out a cannon barrel while it was immersed in cold water. A couple of hours of steady grinding brought the water up to boiling. The heating was steady, too, and apparently ‘inexhaustible.’ Better yet, the initial barrel, the cleaned‑out barrel and the drilled‑out shavings all had the same specific heat so no heat had been extracted from anything. He concluded that heat is an aspect of motion, totally contradicting the leading caloric theories and what was left of phlogiston.”

<chuckle> “He was a revolutionary, after all. But what about ‘Enthalpy‘?”

“Here’s an example. Suppose you’ve got a puddle of gasoline, but its temperature is zero kelvins and somehow it’s compressed to zero volume. Add energy to those waggling molecules until the puddle’s at room temperature. Next, push enough atmosphere out of the way to let the puddle expand to its normal size. Pushing the atmosphere takes energy, too — the physicists call that ‘PV work‘ because it’s calculated as the pressure times the volume. The puddle’s enthalpy is its total energy content — thermal plus PV plus the chemical energy you get when it burns.”

~~ Rich Olcott