Tag: Newton

Carefully Considered Indirection

On By rolcottIn Space Travel, UncategorizedLeave a comment

“C’mon, Vinnie, you’re definitely doing Sy stuff. I ask you a question about how come rockets can get to the Moon easier than partway and you go round the barn with ballistics and cruisers. Stop dodging.”

“Now, Al, Vinnie’s just giving you background, right. Vinnie?”

“Right, Sy, though I gotta admit a lot of our talks have gone that way. So what’s your answer?”

“Nice try, Vinnie. You’re doing fine, so keep at it.”

“Okay. <deep breath> It has to do with vectors, Al, combination of amount and direction, like if you’re going 3 miles north that’s a vector. You good with that?”

“If you say so.”

“I do. Then you can combine vectors, like if you’re going 3 miles north and at the same time 4 miles east you’ve gone 5 miles northeast.”

“That’s a 3-4-5 right triangle, even I know that one. But that 5 miles northeast is a vector, too, right?”

“You got the idea. Now think about fueling a rocket going up to meet the ISS.”

“Sy said it’s 250 miles up, so we need enough fuel to punch that far against Earth’s gravity.”

“Not even close. If the rocket just went straight up, it’d come straight down again. You need some sideways momentum, enough so when you fall you miss the Earth.”

“Miss the Earth? Get outta here!”

“No, really. Hey, Sy, you tell him.”

“Vinnie’s right, Al. That insight goes back to Newton. He proposed a thought experiment about building a powerful cannon to fire horizontally from a very tall mountain. <sketching on paper napkin> A ball shot with a normal load of powder might hit the adjacent valley. Shoot with more and more powder, balls would fly farther and farther before hitting the Earth. Eventually you fire with a charge so powerful the ball flies far enough that its fall continues all around the planet. Unless the cannon blows up or the ball shatters.”

“That’s my point, Al. See, Newton’s cannon balls started out going flat, not up. To get up and into orbit you need up and sideways velocity, like on the diagonal. You gotta calculate fuel to do both at the same time.”

“So what’s that got to do with easier to get to the Moon than into orbit?”

“‘S got everything to do with that. Not easier, though, just if you aim right the vectors make it simpler and cheaper to carry cargo to the Moon than into Earth orbit.”

“So you just head straight for the Moon without going into orbit!”

“Not quite that simple, but you got the general idea. Remember when I brought that kid’s top in here and me and Sy talked about centrifugal force?”

“Do I? And I made you clean up all those spit-wads.”

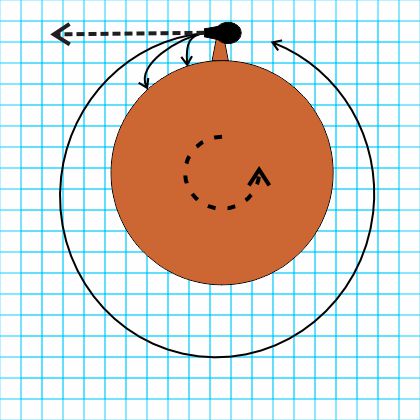
“Yeah, well, suppose that cannon’s at the Equator <adding dotted lines to Sy’s diagram> and aimed with the Earth’s spin and suppose we load in enough powder for the ball to go straight horizontal, which is what it’d do with just centrifugal force.”

“If I’m standing by the cannon it’d look like the ball’s going sideways.”

“Yup. Basically, you get the up‑ness for free. We’re not talking about escape velocity here, that’s different. We’re talking about the start of a Hohmann orbit.”

“Who’s Hohmann?”

“German engineer. When he was a kid he read sci‑fi like the rest of us and that got him into the amateur rocketry scene. Got to be a leader in the German amateur rocket club, published a couple of leading‑edge rocket science books in the 1920s but dropped out of the field when the Nazis started rolling and he figured they’d build rocket weapons. Anyhow, he invented this orbit that starts off tangent to a circle around one planet or something, follows an ellipse to end tangent to a circle around something else. Smooth transitions at both ends, cheapest way you can get from here to there. Kinks in the routing cost you fuel and cargo capacity to turn. Guy shoulda patented it.”

“Wait, an orbit’s a mathematical abstraction, not a thing.”

“Patent Office says it’s a business method, Sy. Check out PAS-22, for example.”

“Incredible.”

~ Rich Olcott

  • Thanks to Ken, who asked another question.

The Cold Equation

On By rolcottIn Space Travel, Uncategorized2 Comments

Afternoon break time. I’m enjoying one of Al’s strawberry scones when he plops one of his astronomy magazines on Vinnie’s table. “Vinnie, you bein’ a pilot and all, could you ‘splain some numbers which I don’t understand? It’s this statistics table for super‑heavy lifter rockets. I think it says that some of them can carry more cargo to the Moon than if they only go partway there. That’s nuts, right?”

Vehicle Payload to LEO GSO Payload TLI Payload
Energia 100 20 32
Falcon Heavy 64 27 28
NASA’s SLS 1b 105 42
SpaceX Starship 100
Yenisei 103 26 28
Yenisei Don 140 30 33
LEO=Low Earth Orbit, GSO = Geosynchronous Orbit, TLI=Trans Lunar Injection
Payloads in metric tons (megagrams)

“Lemme think … LEO is anywhere up to about 2000 kilometers. GSO is about 36000 kilometers out, so it makes sense that with the same amount of fuel and stuff you can’t lift as much out there. TLI … that’s not to the Moon, that’s to a point where you can switch from orbiting the Earth to orbiting the Moon so, yeah, that’s gonna be way farther out, like a couple hundred thousand kilometers or more depending.”

“Depending on what?”

“Oh, lots of things — fuel, orbit, design philosophy—”

“Now wait, you been taking Sy lessons. Philosophy?”

“No, really. There’s two basic ways to do space travel, either you’re ballistic or you’re cruising. All the spacecraft blast‑offs you’ve seen are ballistic. Use up most of your fuel to get a good running start and then basically coast the rest of the way to your target. Ballistic means you gotta aim careful from the get‑go. That’s the difference between ballistic and cruise missiles. Cruisers keep burning fuel and accelerating. That lets ’em change directions whenever.”

“Cruisers are better, right, so you can point at different asteroids? I read about that weird orbit they had to send the Lucy mission on.”

“Actually, Lucy used the ballistic‑and‑coast model. NASA spent a bucketful of computer time calculating exactly where to point and when to lift off so Lucy could visit all those asteroids.”

“Why not just use a cruise strategy and skip around?”

“Cruisers are just fine once you’re up between planets. NASA’s Dawn mission to the Vesta and Ceres asteroids used a cruise drive — but only after the craft rode a boostered Delta‑II ballistic up to low Earth orbit. Nine boosters worth of ballistic. The problem is you’re caught in a double bind. You need to burn fuel to get the payload off the planet, but you need to burn fuel to get the fuel off, too. ‘S called diminishing returns. Hey, Sy, what’s that guy’s name?”

“Which guy?”

“The rocket equation guy, the Russian.”

“Ah. Tsiolkovsky. Lived in a log cabin but wrote a lot about space travel. Everything from rocket theory to airlocks and space stations. What about him?”

“I’m tellin’ Al about rockets. Tsiol… That guy’s equation says if you know how much you need to change velocity and you know your payload mass, you can figure how much fuel you need to burn to do that.”

“With some conditions, Vinnie. There’s a multiplier in there you have to calibrate for fuel, engine design. even whether you’re traveling through water or vacuum or different atmospheres. Then, the equation doesn’t figure in gravity. Oh, and it only works with straight‑line velocity change. If you want to change direction you need to use calculus to figure the—”

“Hey, I just realized why they use boosters!”

“Why’s that, Al?”

“The gravity thing. Gravity’s strongest near the Earth, right? Once the beast gets high enough, you’re not fighting as much gravity. You don’t need the extra power.”

“True, but that’s not the whole picture. The ISS orbit’s about 250 miles up, which puts it about 4250 miles from the planet’s center. Newton’s Law of Gravity says the field all the way up there is still about 88% of what’s at the surface. The real reason is that a booster’s basically a fuel tank. Once you’ve burned the fuel you don’t need the tank and that’s a lot of weight to carry for nothing.”

“Right, tank and engine don’t count as payload so dump ’em.”

“Seems cold‑hearted, though.”

~~ Rich Olcott

Chocolate, Mint And Notation

On By rolcottIn Mathematics, UncategorizedLeave a comment

“But calculus, Mr Moire. Why do they insist we learn calculus? You said that Newton and Leibniz started it but why did they do it?”

“Scoop me a double-dip chocolate-mint gelato, Jeremy, and I’ll tell you about an infamous quarrel. You named Newton first. I expect most Europeans would name Leibniz first.”

“Here’s your gelato. What does geography have to do with it?”

“Thanks. Mmm, love this combination. Part of the geography thing is international history, part of it is personality and part of it is convenience. England and continental Europe have a history of rivalry in everything from the arts to trade to outright warfare. Each naturally tends to favor its own residents and institutions. Some people say that the British Royal Society was founded to compete with the French philosophical clubs. Maybe England’s king appointed Newton as the society’s President to upgrade the rivalry. Dicey choice. From what I’ve read, Newton’s didn’t hate everybody, he just didn’t like anybody. But somehow he ran that group effectively despite his tendency to go full‑tilt against anyone who disagreed with his views.”

“Leibniz did the same thing on the European side?”

“No, quite the opposite. There was no pre‑existing group for him to head up and he didn’t start one. Instead, he served as a sort of Information Central while working as diplomat and counselor for a series of rulers of various countries. He carried on a lively correspondence with pretty much everyone doing science or philosophy. He kept the world up to date and in the process inserted his own ideas and proposals into the conversation. Unlike Newton, Leibniz was a friendly soul, constantly looking for compromise. Their separate calculus notations are a great example.”

“Huh? Didn’t everyone use the same letters and stuff?”

“The letters, yeah mostly, but the stuff part was a long time coming. What’s calculus about?”

“All I’ve seen so far is proofs and recipes for integrating different function types. Nothing about what it’s about.”

Newton approximates arc ABCDEF.

<sigh> “That’s because you’re being taught by a mathematician. Calculus is about change and how to handle it mathematically. That was a hot topic back in the 1600s and it’s still central to Physics. Newton’s momentum‑acceleration‑force perspective led him to visualize things flowing with time. His Laws of Motion made it easy to calculate straight‑line flows but what to do about curves? His solution was to break the curve into tiny segments he called fluxions. He considered each fluxion to be a microscopic straight line that existed for an infinitesimal time interval. A fluxion’s length was its time interval multiplied by the velocity along it. His algebraic shorthand for ‘per time‘ was to put a dot over whatever letter he was using for distance. Velocity along x was ẋ. Acceleration is velocity change per time so he wrote that with a double dot like ẍ. His version of calculus amounted to summing fluxion lengths across the total travel time.”

“But that only does time stuff. What about how, say, potential energy adds up across a distance?”

“Excellent question. Newton’s notation wasn’t up to that challenge, but Leibniz developed something better.”

“He copied what Newton was doing and generalized it somehow.”

“Uh, no. Newton claimed Leibniz had done that but Leibniz swore he’d been working entirely independently. Two lines of evidence. First, Newton was notoriously secretive about his work. He held onto his planetary orbit calculations for years before Halley convinced him to publish. Second, Leibniz and other European thinkers came to the problem with a different strategy. Descartes invented Cartesian coordinates a half‑century before. That invention naturally led the Europeans to plot anything against anything. Newton’s fluxions combined tiny amounts of distance and time; Leibniz and company split the two dimensions, one increment along each component. Leibniz tried out a dozen different notations for the increment. After much discussion he finally settled on a simple d. The increment along x is dx, but x could be anything quantitative. dy/dx quantifies y‘s change with x.”

“Ah, the increments are the differentials we see in class. But those all come from limit processes.”

“Leibniz’ d symbol and its powerful multi‑dimensional extensions carry that implication. More poetry.”

~~ Rich Olcott

Making Things Simpler

On By rolcottIn Mathematics, UncategorizedLeave a comment

“How about a pumpkin spice gelato, Mr Moire?”

“I don’t think so, Jeremy. I’m a traditionalist. A double‑dip of pistachio, please.”

“Coming right up, sir. By the way, I’ve been thinking about the Math poetry you find in the circular and hyperbolic functions. How about what you’d call Physics poetry?”

“Sure. Starting small, Physics has symmetries for rhymes. If you can pivot an experiment or system through some angle and get the same result, that’s rotational symmetry. If you can flip it right‑to‑left that’s parity symmetry. I think of a symmetry as like putting the same sound at the end of each line in rhymed verse. Physicists have identified dozens of symmetries, some extremely abstract and some fundamental to how we understand the Universe. Our quantum theory for electrons in atoms is based on the symmetries of a sphere. Without those symmetries we wouldn’t be able to use Schrodinger’s equation to understand how atoms work.”

“Symmetries as rhymes … okaaayy. What else?”

“You mentioned the importance of word choice in poetry. For the Physics equivalent I’d point to notation. You’ve heard about the battle between Newton and Leibniz about who invented calculus. In the long run the algebraic techniques that Leibniz developed prevailed over Newton’s geometric ones because Leibniz’ way of writing math was far simpler to read, write and manipulate — better word choice. Trying to read Newton’s Principia is painful, in large part because Euler hadn’t yet invented the streamlined algebraic syntax we use today. Newton’s work could have gone faster and deeper if he’d been able to communicate with Euler‑style equations instead of full sentences.”

“Oiler‑style?”

“Leonhard Euler, though it’s pronounced like ‘oiler‘. Europe’s foremost mathematician of the 18th Century. Much better at math than he was at engineering or court politics — both the Russian and Austrian royal courts supported him but they decided the best place for him was the classroom and his study. But while he was in there he worked like a fiend. There was a period when he produced more mathematics literature than all the rest of Europe. Descartes outright rejected numbers involving √‑1, labeled them ‘imaginary.’ Euler considered √‑1 a constant like any other, gave it the letter i and proceeded to build entire branches of math based upon it. Poor guy’s vision started failing in his early 30s — I’ve often wondered whether he developed efficient notational conventions as a defense so he could see more meaning at a glance.”

“He invented all those weird squiggles in Math and Physics books that aren’t even Roman or Greek letters?”

“Nowhere near all of them, but some important ones he did and he pointed the way for other innovators to follow. A good symbol has a well‑defined meaning, but it carries a load of associations just like words do. They lurk in the back of your mind when you see it. π makes you think of circles and repetitive function like sine waves, right? There’s a fancy capital‑R for ‘the set of all real numbers‘ and a fancy capital‑Z for ‘the set of all integers.’ The first set is infinitely larger than the second one. Each symbol carries implications abut what kind of logic is valid nearby and what to be suspicious of. Depends on context, of course. Little‑c could be either speed‑of‑light or a triangle’s hypotenuse so defining and using notation properly is important. Once you know a symbol’s precise meaning, reading an equation is much like reading a poem whose author used exactly the right words.”

“Those implications help squeeze a lot of meaning into not much space. That’s the compactness I like in a good poem.”

“It’s been said that a good notation can drive as much progress in Physics as a good experiment. I’m not sure that’s true but it certainly helps. Much of my Physics thinking is symbol manipulation. Give me precise and powerful symbols and I can reach precise and powerful conclusions. Einstein turned Physics upside down when he wrote the thirteen symbols his General Relativity Field Equation use. In his incredibly compact notation that string of symbols summarizes sixteen interconnected equations relating mass‑energy’s distribution to distorted spacetime and vice‑versa. Beautiful.”

“Beautiful, maybe, but cryptic.”

~~ Rich Olcott

DARTing to A Conclusion

On By rolcottIn Astronomy, Space Travel, Uncategorized2 Comments

The park’s trees are in brilliant Fall colors, the geese in the lake dabble about as I walk past but then, “Hey Moire, I gotta question!”

“Good morning, Mr Feder. What can I do for you?”

“NASA’s DART mission to crash into Diddy’s mos’ asteroid—”

“The asteroid’s name is Didymos, Mr Feder, and DART was programmed to crash into its moon Dimorphos, not into the asteroid itself.”

“Whatever. How’d they know it was gonna hit the sunny side so we could see it? If it hits in the dark, nobody knows what happened. They sent that rocket up nearly a year ago, right? How’d they time that launch just right? Besides, I thought we had Newton’s Laws of Motion and Gravity to figure orbits and forces. Why this big‑dollar experiment to see if a rocket shot would move the thing? Will it hit us?”

“You’re in good form today, Mr Feder.” <unholstering Old Reliable> “Let me pull some facts for you. Ah, Didymos’ distance from the Sun ranges between 1.01 and 2.27 astronomical units. Earth’s at 1.00 AU or 93 million miles, which means that the asteroid’s orbit is 930 000 miles farther out than ours, four times our distance to the Moon. That’s just orbits; Earth is practically always somewhere else than directly under Didymos’ point of closest approach. Mm… also, DART flew outward from Earth’s orbit so if the impact has any effect on the Didymos‑Dimorphos system it’ll be to push things even farther away from the Sun and us. No, I’m not scared, are you?”

“Who me? I’m from Jersey; scare is normal so we just shrug it off. So why the experiment? Newton’s not good enough?”

“Newton’s just fine, but collisions are more complicated than people think. Well, people who’ve never played pool.”

“That’s our national sport in Jersey.”

“Oh, right, so you already know about one variable we can’t be sure of. When the incoming vector doesn’t go through the target’s center of mass it exerts torque on the target.”

“We call that ‘puttin’ English on it.'”

“Same thing. If the collision is off‑center some of the incoming projectile’s linear momentum becomes angular momentum in the target object. On a pool table a simple Newtonian model can’t account for frictional torque between spinning balls and the table. The balls don’t go where the model predicts. There’s negligible friction in space, you know, but spin from an off‑center impact would still waste linear momentum and reduce the effect of DART’s impact. But there’s another, bigger variable that we didn’t think much about before we actually touched down on a couple of asteroids.”

“And that is…?”

“Texture. We’re used to thinking of an asteroid as just a solid lump of rock. It was a surprise when Ryugu and Bennu turned out to be loose collections of rocks, pebbles and dust all held together by stickiness and not much gravity. You hit that and surface things just scatter. There’s little effect on the rest of the mass. Until we do the experiment on a particular object we just don’t know whether we’d be able to steer it away from an Earth‑bound orbit.”

“Okay, but what about the sunny‑side thing?”

“Time for more facts.” <tapping on Old Reliable> “Basically, you’re asking what are the odds the moonlet is in eclipse when DART arrives on the scene. Suppose its orbit is in the plane of the ecliptic. Says here Dimorphos’ orbital radius is 1190 meters, which means its orbit is basically a circle 3740 meters long. The thing is approximately a cylinder 200 meters long and 150 meters in diameter. Say the cylinder is pointed along the direction of travel. It occupies (200m/3740m)=5% of its orbit, so there’s a 5% chance it’s dark, 95% chance it’s sunlit.”

“Not a bad bet.”

“The real odds are even better. The asteroid casts a shadow about 800 meters across. Says here the orbital plane is inclined 169° to the ecliptic so the moonlet cycles up and down. At that tilt and 1190 meters from Didymos, 200‑meter Dimorphos dodges the shadow almost completely. No eclipses. DART’s mission ends in sunlight.”

~~ Rich Olcott

  • Thanks to my brother Ken, who asked the question but more nicely.

Tilting at Black Holes

On By rolcottIn Physics: Black Holes and Relativity, Physics: Newton and Gravity, UncategorizedLeave a comment

“What’s the cause-effect-time thing got to do with black holes and information?”

“We’re getting there, Al. What happens to spacetime near a black hole?”

“Everybody knows that, Sy, spacetime gets stretched and squeezed until there’s infinite time dilation at the Event Horizon.”

“As usual, Vinnie, what everybody knows isn’t quite what is. Yes, Schwarzschild’s famous solution includes that Event Horizon infinity but it’s an artifact of his coordinate system. Al, you know about coordinate systems?”

“I’m a star-watcher, Sy. Sure, I know about latitude and longitude, declination and right ascension, all that stuff no problem.”

“Good. Well, Einstein wrote his General Relativity equations using generalized coordinates, like x,y,z but with no requirement that they be straight lines or at right angles. Schwarzschild solved the equations for a non‑rotating sphere so naturally he used spherical coordinates — radius, latitude and longitude. Since then other people have solved the equations for more complicated cases using more complicated coordinate systems. Their solutions don’t have that infinity.”

“No infinity?”

“Not that one, anyhow. The singularity at the hole’s geometric center is a real thing, not an artifact. So’s a general Event Horizon, but it’s not quite where Schwarzschild said it should be and it doesn’t have quite the properties that everybody thinks they know it has. It’s still weird, though.”

“How so?”

“First thing you have to understand is that when you get close to a black hole, you don’t feel any different. Except for the spaghettification, of course.”

“It’s frames again, ain’t it?”

“With black holes it’s always frames, Vinnie. If you’re living in a distorted space you won’t notice it. Whirl a meter‑long sword around, you’d always see it as a meter long. A distant observer would see you and everything around you as being distorted right along with your space. They’ll see that sword shrink and grow as it passes through different parts of the distortion.”

“Weird.”

“We’re just getting started, Al. Time’s involved, too. <grabbing a paper napkin and sketching> Here’s three axes, just like x,y,z except one’s time, the G one points along a gravity field, and the third one is perpendicular to the other two. By the way, Al, great idea, getting paper napkins printed like graph paper.”

“My location’s between the Physics and Astronomy buildings, Sy. Gotta consider my clientele. Besides, I got a deal on the shipment. What’s the twirly around that third axis?”

“It’s a reminder that there’s a couple of space dimensions that aren’t in the picture. Now suppose the red ball is a shuttlecraft on an exploration mission. The blue lines are its frame. The thick vertical red line shows it’s not moving because there’s no spatial extent along G. <another paper napkin, more sketching> This second drawing is the mothership’s view from a comfortable distance of the shuttlecraft near a black hole.”

“You’ve got the time axis tilted. What’s that about?”

“Spacetime being distorted by the black hole. You’ve heard Vinnie and me talk about time dilation and space compression like they’re two different phenomena. Thing is, they’re two sides of the same coin. On this graph that shows up as time tilted to mix in with the BH direction.”

“How about those twirly directions?”

“Vinnie, you had to ask. In the simple case where everything’s holding still and you’re not too close to the black hole, those two aren’t much affected. If the big guy’s spinning or if the Event Horizon spans a significant amount of your sky, all four dimensions get stressed. Let’s keep things simple, okay?”

“Fine. So the time axis is tilted, so what?”

“We in the distant mothership see the shuttlecraft moving along pure tilted time. The shuttlecraft doesn’t. The dotted red lines mark its measurements in its blue‑line personal frame. Shuttlecraft clocks run slower than the mothership’s. Worse, it’s falling toward the black hole.”

“Can’t it get away?”

“Al, it’s a shuttlecraft. It can just accelerate to the left.”

“If it’s not too close, Vinnie. The accelerative force it needs is the product of both masses, divided by the distance squared. Sound familiar?”

“That’s Newton’s Law of Gravity. This is how gravity works?”

“General Relativity cut its teeth on describing that tilt.”

~~ Rich Olcott

Holes in A Hole?

On By rolcottIn Physics: Black Holes and Relativity, UncategorizedLeave a comment

Mid-afternoon coffee break time so I head over to Al’s coffee shop. Vinnie’s at his usual table by the door, fiddling with some spilled coffee on the table top. I notice he’s pulled some of it into a ring around a central blob. He looks at it for a moment. His mental gears whirl then he looks up at me. “Hey Sy! Can you have a black hole inside another black hole?”

“That’s an interesting question. Quick answer is, ‘No.’ Longer answer is, ‘Sort of, maybe, but not the way you’re thinking.’ You good with that, Vinnie?”

“You know me better than that, Sy. Pull up a chair and give.”

I wave at Al, who brings me a mug of my usual black mud. “Thanks, Al. You heard Vinnie’s question?”

“Everyone on campus did, Sy. Why the wishy-washy?”

“Depends on your definition of black hole.”

Sky-watcher Al is quick with a response. “It’s a star that collapsed denser than a neutron star.”

Vinne knows me and black holes better than that. “It’s someplace where gravity’s so strong that nothing can get out, not even light.”

“Both right, as far as they go, but neither goes deep enough for Vinnie’s question.”

“You got a better one, I suppose?”

“I do, Vinnie. My definitition is that a black hole is a region of spacetime with such intense gravitation that it wraps an Event Horizon around itself. Al’s collapsed star is one way to create one, but that probably doesn’t account for the Event Horizons around supermassive black holes lurking in galactic cores. Your ‘nothing escapes‘ doesn’t say anything about conditions inside.”

“Thought we couldn’t know what happens inside.”

“Mostly correct, which is why your question is as problematical as you knew it was. Best I can do is lay out possibilities, okay? First possibility is that the outer black hole forms around a pre-existing inner one.”

“Can they do that?”

“In principle. What makes a black hole is having enough mass gathered in close proximity. Suppose you have a black hole floating our there in space, call it Fred, and a neutron star comes sidling by. If the two bodies approach closely enough, the total amount of mass could be large enough to generate a second Event Horizon shell enclosing both of them. How long that’d last is another matter.”

“The outer shell’d go away?”

“No chance of that. Once the shell’s created, the mass is in there and the star is doomed … unless the star’s closest approach matches Fred’s ISCO. That’s Innermost Stable Circular Orbit, about three times Fred’s Event Horizon’s half-diameter if Fred’s not rotating. Then the two bodies might go into orbit around their common center of gravity.”

“How’s rotation come into this?”

“If the mass is spinning, then you’ve got a Kerr black hole, frame-dragging and an ISCO each along and against the spin direction. Oh, wait, I forgot about tidal effects.”

“Like spaghettification, right.”

“Like that but it could be worse. Depending on how tightly neutronium holds itself together, which we don’t know, that close approach might be inside the Roche limit. Fred’s gravity gradient might simply shred the star to grow the black hole’s accretion disk.”

“Grim. You said there’s other possibilities?”

“Sorta like the first one, but suppose the total mass comes from two existing black holes, like the collision that LIGO picked up accidentally back in 2014. Suppose each one is aimed just outside the other’s ISCO. Roche fragmentation wouldn’t happen, I think, because each body’s contents are protected inside its own personal Event Horizon. Uhh … darn, that scheme won’t work and neither will the other one.”

“Why not?”
 ”Why not?”

“Because the diameter of an Event Horizon is proportional to the enclosed mass. The outer horizon’s diameter for the case with two black holes would be exactly the sum of the diameters of the embedded holes. If they’re at ISCO distances apart they’re can’t be close enough to form the outer horizon. For the same reason, I don’t think a neutron star could get close enough, either.”

“No hole in a hole, huh?”

“I’m afraid not.”

~~ Rich Olcott

  • Thanks to Alex and Xander, who asked the question.

In vacuo veritas?

On By rolcottIn Cosmology, UncategorizedLeave a comment

“Let’s see if my notes are complete, Mr Moire. We’re crossed off two possible Universe finales — falling into a Big Crunch or expanding forever while making new matter between the galaxies to keep itself in a steady state. Or the Universe might expand to some critical density and then stay there but we mostly ruled that out because a twitch would push it to either crunching or expanding forever. Einstein’s Cosmological Constant might or might not be dark energy but either way, Friedmann’s equation predicts that the Universe will expand exponentially. Is that all the ways we could end?”

“Of course not, Jeremy. The far distant future’s like anything we humans don’t know much about, we make lots of guesses. Vacuum energy, for instance.”

“Anything to do with getting my roommate off the couch when it’s their turn to do the floors?”

“Very funny, but no. The notion of ‘vacuum‘ has a history. Aristotle said it’s empty space and that’s nothing and you can’t talk about nothing, but of course that’s exactly what he was doing. It wasn’t until Newton’s day that we developed dependable technologies for producing and investigating ‘nothing.’ Turns out that a good vacuum’s hard to find and even outer space is a lot busier than you might think.”

“Yeah, Jim in the Physics lab says he’s working with Ultra‑High Vacuum, a millionth of a millionth of an atmosphere, and the molecules left in the apparatus still cause problems.”

“Wonder how many molecules that is. Time for Old Reliable. <muttering> Avagadro’s Number, 22.4 liters, 10-12 atmospheres … Wow, there’s nearly 30 billion molecules per liter in his rig, a couple hundred times more if he chills it. <scrolling> This Wikipedia article says the solar wind runs only ten thousand protons per liter; interstellar medium’s about a tenth of that. But all those are physical vacuums. Theoretical vacuums are completely empty except they’re sort‑of not.”

“How could they be empty but not? Is that a Schrödinger joke?”

“No, but it does point up how the word has acquired multiple technical meanings. Newton’s concept of a vacuum was basically equivalent to Aristotle’s — simply a space with no matter in it. Two centuries later, Maxwell pointed the way to electric and magnetic fields which meant we needed to define a new vacuum with no such fields. Einstein added his proviso about the speed of light in a vacuum but that was okay. Then along came quantum and strings and several new kinds of vacuum.”

“Why would we need new definitions? Nothing’s nothing, isn’t it?”

“Not necessarily in theory, and that’s the point. For instance, you might use a Maxwell‑inspired theory to think about how a certain charged object behaves in a certain electromagnetic field. You can’t isolate the field’s effects unless you can add it to a theoretical space containing no objects or electromagnetic fields. Make sense?”

“And that’s a Maxwell vacuum? Seems reasonable. Then what?”

“Quantum theories go in the other direction. They start by assuming that Maxwellian vacuums can’t exist, that space itself continually produces virtual particles from their associated fields.”

“Um, conservation of mass?”

“Valid question. This may feel like dodging, but there’s math and experiment to back it up. What’s really conserved, we think, is mass‑energy. Particles, anti‑particles and energy fluctuations averaging to zero over finite time intervals. A dab of energy concentrated to create a particle’s mass? No problem, because that particle will be annihilated and release its energy equivalent almost immediately. To replace the Maxwellian vacuum, quantum theorists co‑opted the word to refer to a system’s lowest possible quantum state or maybe the lowest possible set of states, depending on which kind of calculation is underway. The cosmology people picked up that notion and that’s when the doom‑saying started.”

“Awright, now we’re getting somewhere. What’s their vacuum like?”

“From what I’ve seen, a tall stack of ‘if‘s and hand‑waving. The idea is that our Universe may not be in the lowest possible quantum state and if so, sometime in the next 188 billion years we could suddenly drop from false to true vacuum, in which case everything goes haywire. I’m not convinced that the Universe even has a quantum state. Don’t panic.”

~~ Rich Olcott

Constant’s Companion

On By rolcottIn CosmologyLeave a comment

“It’s like Mark Twain said, Jeremy — ‘History may not repeat itself, but it rhymes.‘ Newton identified gravity as a force; Einstein proposed the Cosmological Constant. Newton worked the data to develop his Law of Gravity; Friedmann worked Einstein’s theory to devise his model of an exponentially expanding Universe. Newton was uncomfortable with gravity’s ability to act at a distance; Einstein called the Cosmological Constant ‘his greatest blunder.’ The parallels go on.”

“Why didn’t Einstein like the Constant if it explains how the Universe is expanding?”

“It wasn’t supposed to. Expanding Universes weren’t in fashion a century ago when Einstein wrote that paper. At the time everyone including Einstein thought we live in a steady state universe. His first cut at a General Relativity field equation implied a contracting universe so he added a constant term to balance out the contraction even though it made the dynamics look unstable — the Constant had to have just the right value for stability. A decade later Hubble’s data pointed to expansion and Friedman’s equations showed how that can happen.”

“I guess Einstein was embarrassed about that, huh, Mr Moire?”

“Well, he’d thought all along that the Constant was mathematically inelegant. Besides, the Constant isn’t just a number or a term in an equation, it’s supposed to represent a real process in operation. Like Newton’s problem with gravity, Einstein couldn’t identify a mechanism to power the Constant.”

“Power it to do what?”

“Think about universal constants, like the speed of light or the electron charge. Doesn’t matter where you are or how fast you’re traveling in which inertial frame, they’ve got the same values. If the Constant is indeed a constant, it contributes equally to cosmological dynamics from every position in space, whether inside a star or millions of lightyears from any galaxy. Every point must exert the same outward force in every direction or there’d be swirling. And it multiplies — every instant of general expansion makes new points in between the old points and they’ll exert the same force, too.”

“That’s what makes it exponential, right?”

“Good insight. It’s a pretty weak force per unit volume, weaker than gravity. We know that because galaxies and galaxy cluster structures maintain integrity even as they’re drifting apart from each other. Even so, a smidgeon of force from each unit volume in space adds up to a lot of force. Multiply force by distance traveled — that’s a huge amount of energy spent against gravity. The big puzzle is, what’s the energy source? Most of the astrophysics community nominates dark energy to power the Cosmological Constant but that’s not much help.”

“As Dr Prather says in class, Mr Moire, ‘You sound tentative. Please expound.‘ Why wouldn’t dark energy be the power source?”

“In Physics we use the word ‘energy‘ with a very specific meaning. Yes, it gets heavy use with sloppy meanings in everything from show business to crystal therapy, but in hard science nearly every serious research program since the 18th Century has entailed quantitative energy accounting. The First Law of Thermodynamics is conservation of energy. Whenever we see something heating up, a chemical reaction running or a force being applied along a distance, physicists automatically think about the energy being expended and where that energy is coming from. Energy’s got to balance out. But the Constant breaks that rule — we have no idea what process provides that energy. Calling the source ‘dark energy‘ just gives it a name without explaining it.”

“Isn’t the missing energy source evidence against Friedmann’s and Einstein’s equations?”

“That’s a tempting option and initially a lot of researchers took it. Unfortunately, it seems that dark energy is a thing. Or maybe a lot of little things. Several different lines of evidence say that the Constant constitutes twice as much mass‑energy as all normal and dark matter combined. Worse yet, as the Universe expands that share will increase.”

“Wait, will the dark energy invade normal matter and break us up?”

“People argue about that. Normal matter’s held together by electromagnetic forces which are 1038 times stronger than gravity, far stronger yet than dark energy. Dark matter’s gravity helps to hold galaxies together, but who knows what holds dark matter together?”

~~ ROlcott

Three Phases of Ever

On By rolcottIn Cosmology, UncategorizedLeave a comment

“So if the Universe isn’t in a steady state and it’s not heading for a Big Crunch, I guess it’s getting bigger forever, huh?”

“Careful, Jeremy, the Universe expansion could maybe reach a stopping point if it happened to hold exactly the right amount of mass‑energy. The expansion could just stop when forces balance out.”

“What forces, Mr Moire? There’s gravity pulling everything together so what’s pushing them apart?”

“That is an excellent question, one that we don’t yet have an answer for. We’re about where Newton was with gravity. There was a lot of observational evidence, he had a name for it and knew how to calculate its effects, but he didn’t know how it worked. That’s us with Einstein’s Cosmological Constant.”

“Observational evidence — we can actually see things accelerate?”

“Not any one object speeding up. Human lifetimes are too short to measure acceleration in galaxies a hundred thousand lightyears across. No, we use the same strategy that Hubble used — measure many galaxies at different distances from us and graph recession speed against distance. During the century since Hubble we’ve greatly improved our estimates of astronomical speeds and distances. Dividing the known speed of light into a galaxy’s measured distance tells us time since it emitted the photons we see. Our findings confirm Hubble’s general conclusion — on average, older photons come from galaxies that fly away faster. Hubble thought that the relation was linear but our fine‑tuned numbers show otherwise. The data says that after the first few seconds the Universe stretched at a steady rate for only the first ⅔ of its life. The stretch has been accelerating since then.”

“Why wasn’t it accelerating since the beginning? Did someone cut in the afterburner?”

“More like turned one off. The evidence and theory we have so far indicate the Universe has seen a succession of phases dominated by different processes. You’ve probably heard of inflation—”

“Have I? You should see what they want for a burger these days!”

“Not that sort of inflation, but I know how you feel. No, I’m referring to cosmic inflation, very early in the Big Bang sequence, when the Universe expanded by a factor of 1026 within a tiny fraction of a second. It was driven by enormously powerful radiation‑linked effects we don’t understand that finally ran out of steam and let lower‑energy processes take over.”

“How’d that happen?”

“We don’t know. The general principle is that one process so dominates what’s going on in a phase that nothing else matters, until for some reason it stops mattering and we’re in a new phase with a different dominant process. The early Universe was controlled by radiative processes until things cooled off enough for particles to form and persist. That changed the game. Gravity dominated the next 8 billion years. Particles clumped together, atoms then dust then solar systems into larger and larger structures with bigger spaces between them. About 5 billion years ago the game changed again.”

“So early on there weren’t even atoms, huh? Wow. What was the next game‑changer?”

“Thanks to Einstein and Friedmann’s work we’ve got at least a guess.”

“Friedmann?”

“Alexander Friedmann. He was a Russian physicist, used Einstein’s General Relativity results to derive three equations that together model the dynamics of the overall scale of the Universe using just a few estimates for current conditions. His equations give acceleration as the difference of two terms. The positive term is simply proportional to Einstein’s Constant. The negative term depends on both average mass density and pressure. Take a moment to think.”

“Umm… Positive is acceleration, negative is deceleration, density and pressure go down … If the negative term gets smaller than the positive one, acceleration increases, right?”

“It does, and we think the constant term has been increasingly dominant for 5 billion years. Something else to consider — the equation’s result is in terms of scale change divided by current scale. What’s it mean if that ratio’s a positive constant?”

“Change by a constant positive percentage … that’s exponential growth!”

“I thought you’d recognize it. Einstein’s Constant implies the scale of the Universe grows at an exponentially accelerating rate. We’re now in the Cosmological Constant phase.”

In Russian, Aleksandr Aleksandrowitsch Fridman

~~ Rich Olcott