The Not-so-dangerous Banana

On October 7, 2024November 30, 2025 By rolcottIn Astronomy: Techniques, Physics: Quantum Mechanics, UncategorizedLeave a comment

“Y’know, Cathleen, both our ladders boil down to time. Your Astronomy ladder connects objects at different times in the history of the Universe. My Geology ladder looks back into the Solar System’s history.”

“As an astronomer I normally think of parsecs or lightyear distances but you have a point, Kareem. Edwin Hubble linked astronomical space with time. Come to think of it, my cosmologist colleagues work almost exclusively in the time domain, like ‘T=0 plus a few lumptiseconds.’ Billions of years down to that teeny time interval — how does your time ladder compare?”

“Lumptiseconds out to a hundred trillion times the age of the Universe. I win.”

“C’mon, Kareem.”

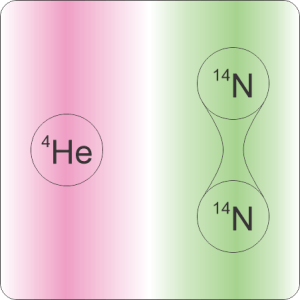
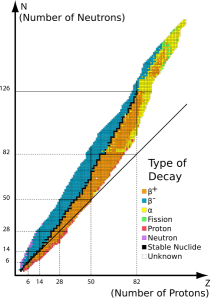
“No, really, Sy. My ladder uses isotopes. Every carbon atom has 6 protons in the nucleus, right? Carbon‑12 adds 6 neutrons and it’s stable but another isotope, carbon‑14, has 8 neutrons. It’s radioactive — spits out an electron and becomes stable nitrogen‑14 with 7 and 7. Really heavy isotopes like uranium‑238 spit out alpha particles.”

“Wait, if carbon‑14 spits out an electron doesn’t that make it a carbon ion?”

“Uh‑uh, Cathleen, the electron comes out of the nucleus, not the electron cloud. It’s got a hundred thousand times more energy than a chemical kick could give it. Sy could explain—”

“Nice try, Kareem, this is your geologic time story. Let’s stay with that.”

“If I must. So, the stable isotopes last forever, pretty much, but the radioactive ones are ticking bombs with random detonation times.”

“What’s doing the ticking? Surely there’s no springs or pendulums in there.”

“Quantum, Cathleen. Sy’s trying to stay out of this so I’ll give you my outsider answer. I picture every kind of subatomic particle constantly trying to leave every nucleus, butting their little heads bazillions of times a second against walls set up by the weak and strong nuclear forces. Nearly every try is a bounce‑back, but one success is enough to break the nucleus. Every isotope has its own personal set of parameters for each kind of particle — wall height, wall thickness, something like an internal temperature ruling how hard the particles hit the walls. The ticking is those head‑butts; the randomness comes from quantum’s goofy rules somehow. How’s that, Sy?”

“Good enough for jazz, Kareem. Carry on.”

“Right. So every kind of radioisotope is characterized by what kinds of particle it emits, how much energy each kind has after busting through a wall, and how often that happens in a given sample size. And the isotope’s chemistry, of course, which is the same as every other isotope that has the same number of protons. The general rule is that the stable isotopes have maybe a few more neutrons than protons but nearly every element has some unstable isotopes. The ones with too many neutrons, like carbon‑14, emit electrons as beta particles. They go up a square in the Periodic Table. Too few and they drop down by emitting a positron.”

“All those radioactive stand‑ins for normal atoms. Sounds ghastly. Why are we still here and not all burnt up?”

“First, when one of these atoms decays by itself it’s a lot of energy for that one atom, but the energy spreads out as heat across many atoms. Unless a bunch of atoms crumble at about the same time, there’s only a tiny bit of general heating. The major biological danger from radioactivity comes from spit‑out particles breaking protein or DNA molecules.”

“Mutated, not burnt.”

“Mm‑hm. Second, the radioactives are generally rare relative to their stable siblings. In many cases that’s because the bad guys, like aluminum‑26, have had time to decay to near‑zero. That banana you’re eating has about half a gram of potassium atoms but only 0.012% are unstable potassium‑40. Third, an isotope with a long half‑life doesn’t lose many atoms per unit time. A kilogram of tellurium‑128, for instance, loses 2000 atoms per year. The potassium‑40 in your banana has a half‑life of nearly 2 million years. Overall, it releases only about 1300 beta particles per second producing less than a nanowatt of heat‑you‑up power. Not to worry.”

“Two million years? How do you measure something that slow?”

~~ Rich Olcott

EROs Atop A Ladder

On September 30, 2024November 30, 2025 By rolcottIn Astronomy: Techniques, UncategorizedLeave a comment

“‘That’s where the argument started‘? That’s right up there with ‘Then the murders began.’ Cathleen Cliff‑hanger strikes again.”

<giggling> “Gotcha, Sy, just like always. Sorry, Kareem, we’ve had this thing since we were kids.”

“Don’t mind me, but do tell him what’s awry with the top of your galactic distance ladder.”

“I need to fill you in first about the ladder’s framework. We know the distances to special ‘standard candles’ scattered across the Universe, but there’s oodles of other objects that aren’t special that way. We can’t know their distances unless we can tie them to the candles somehow. Distance was Edwin Hubble’s big thing. Twenty years after Henrietta Swan Leavitt identified one kind of candle, Hubble studied the light from them. The farthest spectra were stretched more than the closest ones. Better yet, there was a strict relationship between the amount of stretch, we call it the z factor, and the candle’s distance. Turns out that everything at the intergalactic scale is getting farther from everything else. He didn’t call that expansion the Hubble Flow but we do. It comes to about 7% per billion lightyears distance. z connects candle spectrum, object spectrum and object distance. That lets us calibrate successive overlapping steps on the distance ladder, one candle type to the next one.”

“A constant growth rate — that’s exponential, by definition. Like compound interest. The higher it gets, it gets even higher faster.”

“Right, Kareem, except that in the past quarter-century we’ve realized that Hubble was an optimist. The latest data suggests the expansion he discovered is accelerating. We don’t know why but dark energy might have something to do with it. But that’s another story.”

“Cathleen, you said the distance ladder’s top rung had something to do with surface brightness. Surface of what?”

“Galaxies. Stars come at all levels of brightness. You can confirm that visually, at least if you’re in a good dark‑sky area. But a galaxy has billions of stars. When we assess brightness for a galaxy as a whole, the brightest stars make up for the dimmest ones. On the average it’ll look like a bunch of average stars. The idea is that the apparent brightness of some galaxy tells you roughly how many average stars it holds. In turn, that gives you a rough estimate of the galaxy’s mass — our final step up the mass ladder. Well, except for gravitational lensing, but that’s another story.”

“So what’s wrong with that candle?”

“We didn’t think anything was wrong until recently. Do you remember that spate of popular science news stories a year ago about giant galaxies near the beginning of time when they had no business to exist yet?”

“Yeah, there was a lot of noise about we’ll have to revise our theories about how the Universe evolved from the Big Bang, but the articles I saw didn’t have much detail. From what you’ve said so far, let me guess. These were new galaxy sightings, so probably from James Webb Space Telescope data. JWST is good at infra‑red so they must have been looking at severely stretched starlight—”

“z-factor near 8″

“— so near 13 billion lightyears old, but the ‘surface brightness’ standard candle led the researchers to claim their galaxies held some ridiculous number of stars for that era, at least according to current theory. How’d I do?”

“Good guess, Sy. That’s where things stood for almost a year until scientists did what scientists do. A different research group looking at even more data as part of a larger project came up with a simpler explanation. Using additional data from JWST and several other sources, the group concentrated on the most massive galaxies, starting with low‑z recent ones and working back to z=9. Along the way they found some EROs — Extremely Red Objects where a blast of infra‑red boosts their normal starlight brightness. The researchers attribute the blast to hot dust associated with a super‑massive black hole at each ERO’s center. The blast makes an ERO appear more massive than it really is. Guess what? The first report’s ‘ridiculously massive’ early galaxies were EROs. Can’t have them in that top rung.”

“Kareem, how about the rungs on your ladder?”

~~ Rich Olcott

One Step After Another

On September 23, 2024November 30, 2025 By rolcottIn Astronomy: Techniques, UncategorizedLeave a comment

Mid-afternoon, time for a coffee break. As I enter Cal’s shop, I see Cathleen and Kareem chuckling together behind a jumble of Cal’s distinctive graph‑lined paper napkins. “What’s the topic of conversation, guys?”

“Hi, Sy. Kareem and I are comparing ladders.”

I look around, don’t see anything that looks like construction equipment.

“Not that kind, Sy. What’s your definition of a ladder?”

“Getting down to definitions, eh, Kareem? Okay, it’s a framework with steps you can climb up towards something you can’t reach.”

“Well, there you go.”

“Not much help, Cathleen. What are you really bantering about?”

“Each of our fields of study has a framework with steps that let us measure something that’d be way out of reach without it.”

“You’ll appreciate this, Sy — our ladders even use different math. The steps on Cathleen’s ladder are mostly linear, mine are mostly exponential.”

“And they’re both finicky — you have to be really careful when using them.”

“And they’ve both recently had adjustments at the top end.”

“I can see the fun, I think. How about some specifics?”

They exchange a look, Kareem gestures ‘after you‘ and Cathleen opens. “Mine’s in astrometry, Sy, the precise recording of relative positions. Tycho Brahe’s numbers were good to a few dozen arcseconds—”

“Arcsecond?”

“¹/₆₀ of an arcminute which is ¹/₆₀ of a degree which is ¹/₃₆₀ of a full circle around the sky. Good enough in Newton’s day for him to explain planetary orbits, but we’ve come <ahem> a long way since then. The Gaia telescope mission can resolve certain objects down to a few microarcseconds but that’s only half the problem.”

“Let me guess — you have angles but you don’t have distances.”

“Bingo. Distance is astrometry’s biggest challenge.”

“Wait, Newton’s Law of Gravity includes r as the distance between objects. For that matter, Kepler’s Laws use r² and r³. Couldn’t you juggle them around to evaluate r?”

“Nope. Kepler did ratios, not absolute values. Newton’s Law has r² but you can rewrite it as F ² = GMm/r² = G(M/r)(m/r), G times the product of two mass‑to‑distance ratios. Newton’s G is our least‑accurate physical constant and we don’t have good handles on either of those numerators. Before space flight we just had mass ratios like M/m. We only discovered the Moon’s absolute mass when we orbited it with spacecraft of known mass. That’s the lowest rung on our mass ladder. Inside the Solar System we go step by step with orbit ratios. Outside the system everything’s measured relative to Solar mass.”

“I’m getting the ladder idea. So how do you distances?”

“Lowest rung is parallax, like binocular vision. You look at something from two different points a known distance apart. Measure the angle between the sight‑lines. Figure the triangles to get the something’s distance. The earliest example I know of was in the mid‑1700s when astrometers thousands of miles apart on Earth watched Venus cross the Sun’s disk. Each recorded the precise time they saw Venus touch the Sun’s disk. Given the time shift and the on‑Earth distance, some trigonometry gave them the Earth‑Venus distance. That put a scale to Newtonian orbital diagrams. Parallax across the width of Earth’s orbit yielded stellar distances out to thousands of lightyears with Hubble. We expect ten times better from Gaia.”

“That gets you maybe across the Milky Way. What about farther out?”

“Several ingenious variations on the parallax idea, but mostly standard candles.”

“Candles?”

“Suppose you measure the brightness of a candle that’s a known distance away and there’s an equally luminous candle some unknown distance away. Measured brightness falls as the square of the distance, so if the second candle appears half as bright it’s four times the distance and so on. Climbing the cosmic distance ladder is going from one kind of uniformly‑luminous candle to another kind farther away.”

“Such as?”

“We know how brightness relates to bright‑dim‑bright cycle time for several types of variable stars. That gets us out to 30 million lightyears or so. Type I‑a supernovas act as useful candles out to a billion lightyears. Beyond that we can use galaxy surface brightness. That’s where the recent argument started.”

~ Rich Olcott

Thanks to Ken Burke for mentioning tellurium‑128’s septillion‑year half‑life.

A Big Purple Snowball

On September 9, 2024November 30, 2025 By rolcottIn Astronomy: Planetary Science, Crazy Theories, UncategorizedLeave a comment

Cathleen’s back at the mic. “Okay, folks, now for the third speaker in tonight’s Crazy Theory seminar. Kareem, you have the floor.”

“Thanks, Cathleen. Some of you already know I do old‑rock geology. If a rock has a bone in it, I’m not interested. Paleontology to me is like reading this morning’s newspaper. So let me take you back to Precambrian times when Earth may have been purple.”

Kareem’s a quiet guy but he’s got the story‑teller’s gift, probably honed it at field expedition campfires, so we all settle back to listen.

“Four and a half billion years ago, Earth was bright orange. That’s not the color it reflected, that’s the color it glowed. You’ve all seen glass‑blowers at work, how the material gives off a bright orange light coming out of the flame or furnace, soft and ready to be formed. That’s what the planet’s surface was like after its Moon‑birthing collision with Theia. Collisions like that release so much heat that there’s no rocks, just layers of smooth molten glassy slag floating on fluid silicates and nickel‑iron like in a blast furnace. No atmosphere, all the volatiles have been boiled off into space. Got the picture?”

General nodding, especially from maybe‑an‑Art‑major who’s good at pictures.

“Time passes. Heat radiating away cools the world from the outside inward. Now the surface is a thin glassy cap, black like obsidian and basalt, mostly smooth. The cooling contracting cap fractures from the tension while the shrinking interior pulls inward, slow but not gentle. The black glassy surface becomes low craggy mountains and razor‑rubble, sharp enough to slice hiking boots to ribbons. There’s no erosive wind or water yet to round things off. Everything stays sharp‑edged.”

Voice from the back of the room — “Where’s our water from then?”

“Good question. Could be buried water that never got the chance to escape past the cap, could be water ferried in on icy comets or worldlets. People argue about it and I’m not taking sides. The planet gets a new color after it cools enough to hold onto water molecules however they got there — but that water doesn’t stay on the surface. Raindrops hitting still‑hot rock hiss back into steamy clouds. If you were on the moon at the time you’d see a white‑and‑grey Earth like Jupiter’s curdled cloud-tops. Visualize a series of million‑year Hurricane Debbies, all over the world.”

He pauses to let that sink in.

“When things finally cool down enough to allow surface water there’s oceans, but they’re not blue. Millions of years of wind and water erosion have ground the sharp rubble to spiky dust. Most of the thrust‑raised mountains, too. Much of the dust is suspended or dissolved in the ocean turning it black. For a while. The dust is loaded with minerals, especially sulfides, very nutritious for a group of not‑quite bacteria called Archaea that eat sulfides using a molecule that’s powered by green light but reflects red and blue. When the Archaea take over, the oceans look magenta from the reflected red and blue.”

Maybe‑an‑Art‑major giggles.

“Next major event, we think, was the Huronian Glaciation, when most or all of the Earth was a solid white because it was covered with ice. Killed off most or the Archaea. When that melted, different parts of the ocean turned black from floating dead Archaea and and then milky turquoise from sulfur particles. Next stage was purple, from a different group of sulfur‑eating purple almost‑bacteria. Then we had snowball whiteness again, which gave green‑reflecting chlorophyll‑users a chance to take over, clear our the sulfur and leave the oceans blue.”

VBOR — “That’s your Crazy Theory?”

“No, that’s mostly mainstream. Question is, what terminated the deepfreezes? Lots of ideas out there — solar dimming and brightening, different combinations of CO₂ and methane from volcanoes or bacteria, even meteorites. Anyone remember Ian Malcom’s repeated line in the Jurassic Park movies?”

Everyone — “Life will find a way!”

“Right on. My crazy’s about the two almost‑bacteria. Suppose each kind managed to infiltrate their day’s Great Extinction glaciers. Suppose planet‑wide bacterial purple pigments absorbed sunlight’s energy, melting the ice. Karma, yes?”

~ Rich Olcott

To Fly on Another World

On August 19, 2024November 27, 2025 By rolcottIn Astronomy: Planetary Science, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

“Uncle Sy, why is PV=nRT the Ideal Gas Equation? Is it because it’s so simple but makes sense anyway?”

“It is ideal that way, Teena, but it’s simply an equation about gases that are ideal. Except there aren’t any. Real gases come close but don’t always follow the rule.”

“Why not? Are they sneaky?”

“Your kind of question. We like to think of gas particles as tiny ping‑pong balls that just bounce off of each other like … ping‑pong balls. That’s mostly true most of the time for most kinds of gas. One exception has to do with stickiness. Water’s one of the worst cases because its H₂O molecules like to chain up. When two H₂Os collide, if they’re pointed in the right directions they share a hydrogen atom like a bridge and stick together. If that sort of stickiness happens a lot then the quantity measure n acts like it’s less than we’d expect. That makes the PV product smaller.”

“I bet that doesn’t happen much when the gas is really hot. Two particles might stick and then BANG! another particle hits ’em and breaks it up!”

“Good thinking and that’s true. But there’s another kind of exception that holds even at high temperatures. A well‑behaved gas is mostly empty space because the ping‑pong balls are far apart unless they’re actually colliding. But suppose you squeeze out nearly all of the empty space and then try to squeeze some more.”

“Oh! The pressure gets even bigger than the equation says it should because you can’t squeeze the particles any smaller than they are, right?”

“Exactly.”

“Well, if the equation has these problems, why do we even use it at all?”

“Because it’s good enough, enough of the time, and we know when not to use it. I’ll give you an example. One of my clients wanted to know air density at ground level on Saturn’s moon Titan and all the planets that have an atmosphere.” <showing Old Reliable’s screen> “I found the planet data I needed in NASA’s Planetary Science website, but I had to do my own calculation for Titan. The pressure’s not crazy high and the temperature’s chilly but not quite cold enough to liquify nitrogen so the situation’s in‑range for the Ideal Gas Equation.”

“What’s a Pa?”

“That’s the symbol for a pascal, the unit of pressure. kPa is kilopascals, just like kg is kilograms. Earth’s atmospheric pressure is about 100 kPa.”

“Reliable says Wikipedia says Titan’s air is mostly nitrogen like Earth’s air is. Titan’s just a moon so it has to be smaller than Earth so its gravity must be smaller, too. Why is its atmosphere so much denser?”

“The cold. Titan’s air is 200 kelvins colder than Earth’s average temperature. You’re right, an individual gas particle feels a smaller pull of gravity on Titan, but it doesn’t have much kinetic energy to push its neighbors away so they all crowd closer together.”

“Why in the world does your client want to know that density number?”

“Clients rarely give me reasons. I suspect this has to do with designing a Titan‑explorer aircraft.”

“Ooo! Wait, what does that have to do with air density?”

“It has to do with how hard the machine has to work to push itself up. It’ll probably have horizontally spinning blades that push the air downwards, like helicopters do. With a setup like that, the lift depends on the blade’s length, how fast it’s spinning, and how dense the air is. If the air is dense, like on Titan, the designers can get the lifting thrust they need with short blades or a slow spin. On Mars the density’s only 2% of Earth’s so Ingenuity‘s rotors were 4 feet across and spun about ten times faster than they’d have to on Earth.”

“What about on our helium‑oxygen Earth?”

“That’s pretty much the same calculation. Give me a sec.” <tapping on Old Reliable’s screen> “Gas density would be a tenth of Earth’s, but a HeO‑copter would have to work against full‑Earth gravity. Huge blades rotating at supersonic speeds. Probably not a practical possibility.”

“Aw.”

“Yeah.”

~ Rich Olcott

The Ideal Gas Game

On August 12, 2024November 27, 2025 By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Fundamentals, UncategorizedLeave a comment

“But Uncle Sy, you never did answer my real question!”

“What question was that, Teena?”

“About the helium planet. With oxygen. Oh, I guess I never did get around to asking that part of it. You side‑tracked us into how a helium‑oxygen atmosphere would be unstable unless it was really cold or the planet had more gravity than Earth so the helium wouldn’t fly away. But what I wanted to know was, what would it be like before the helium left? Like, could we fly a plane there?”

“Mmm, let’s get a leetle more specific. You asked about swapping all of Earth’s atmospheric nitrogen with helium. Was that one helium atom for each nitrogen molecule or each nitrogen atom?”

“What difference would that make?”

“Mass, to begin with. A helium atom weighs about ¹/₃ of a nitrogen atom, ¹/₇ of a nitrogen molecule. The atmospheric pressure we feel is the weight of all the air molecules above us. Swap out 80% of those molecules for something lighter, pressure goes down whether we swap helium for molecules or helium for atoms. We could calculate either one. But the change would be much harder to calculate for the atom‑for‑atom swap.”

“Why?”

“Mmm, have you gotten into equations yet in school?”

“You mean algebra, like 3x+7=8x+2? Yeah, they’re super‑easy.”

“This won’t even be as complicated as that. Here’s a famous Physics equation called The Ideal Gas Law — PV=nRT. Each letter stands for one quantity. Two adjacent quantities are multiplied together, okay? The pressure in a container is P, the container’s volume is V, T is the absolute temperature, and n is a measure of how much gas is in there.”

“You skipped R.”

“Yes, I did. It’s a constant number. Its job is to make all the units come out right. For instance, if the pressure’s in atmospheres, the volume’s in liters, n is in grams of helium and the temperature is in kelvins, then R is 0.021. Suppose you’re holding a balloon filled with helium and it’s at room temperature. What can you say about the gas?”

“Umm, all the nRT stuff doesn’t change so P times V, whatever it is, doesn’t change either.”

“If we let it fly upward until the pressure was only half what it is here…?”

“Then V would double. The balloon would get twice as big. Unless it burst, right?”

“You got the idea. Okay, now let’s fiddle with the right-hand side. Suppose we double the amount of helium.”

“P times V must get bigger but we don’t know which one.”

“Why not both?”

“Wooo… Each one could get some bigger… Oh, wait, I’m holding the balloon so the pressure’s not going to change so the balloon gets twice bigger.”

“Good thinking. One more thing and we can get back to your difference question. The Ideal Gas Law doesn’t care what kind of gas you’re working with. All the n quantity really cares about is how many particles are in the gas. A particle can be anything that moves about independently of anything else — helium atom or nitrogen molecule, doesn’t matter. If you change the definition of what n is measuring, all that happens is you have to adjust R so the units come out right. Then the equation works fine. Next step—”

“Wait, Uncle Sy, I want to think this atom‑or‑molecule thing through for myself. I’m gonna ignore R times T because both of them stay the same. So if we swap one atom of helium for one molecule of nitrogen, the number of particles doesn’t change and PV doesn’t change. But if we swap one atom of helium for each atom of nitrogen then n doubles and so does PV. But if we do that for the whole atmosphere then we can’t say that the pressure won’t change because the atmosphere could just expand and that’s the V but the pressures are all different as you go higher up anyway. Oh, wait, T changes, too, because it’s cold up there. It’s complicated, isn’t it?”

“It certainly is. Can we stick to just the simple atom‑for‑molecule swap?”

“Uh‑huh.”

~~ Rich Olcott

Thanks again, Xander, and happy birthday. Your question was deeper than I thought.

A Virial Homework Problem

On July 22, 2024November 28, 2025 By rolcottIn Astronomy: Techniques, Physics: Entropy and Thermodynamics, Uncategorized1 Comment

“Uh, Mr Moire? Would you mind if we used Old Reliable to do the calculations on this problem about the galaxy cluster’s Virial?”

Data extracted and re-scaled from Fig 2 of Smith (1936), The Mass of the Virgo Cluster

“Mm, only if you direct the computation, Jeremy. I want to be able to face Professor Hanneken with a clear conscience if your name ever comes up in the conversation. Where do we start?”

“With the data he printed here on the other side of the problem sheet. Old Reliable can scan it in, right?”

“Certainly. What are the columns?”

“The first one’s clear. The second column is the distance between the galaxy and the center of the cluster. Professor Hanneken said the published data was in degrees but he converted that to kiloparsecs to get past a complication of some sort. The third column is, umm, ‘the relative line‑of‑sight velocity.’ I understand the line‑of‑sight part, but the numbers don’t look relativistic.”

“You’re right, they’re much smaller than lightspeed’s 300,000 km/s. I’m sure the author was referring to each galaxy’s motion relative to the other ones. That’s what the Virial’s about, after all. I’ll bet John also subtracted the cluster’s average velocity from each of the measured values because we don’t care about how the galaxies move relative to us. Okay, we’ve scanned your data. What do we do next?”

“Chart it, please, in a scatter plot. That’s always the first thing I do.”

“Wise choice. Here you go. What do we learn from this?”

“On the whole it looks pretty flat. Both fast and slow speeds are spread across the whole cluster. If the whole cluster’s rotating we’d see faster galaxies near the center but we don’t. They’re all moving randomly so the Virial idea should apply, right?”

“Mm-hm. Does it bother you that we’re only looking at motion towards or away from us?”

“Uhh, I hadn’t thought about that. You’re right, galaxy movements across the sky would be way too slow for us to detect. I guess the slowest ones here could actually be moving as fast as the others but they’re going crosswise. How do we correct for that?”

“Won’t need much adjustment. The measured numbers probably skew low but the average should be correct within a factor of 2. What’s next?”

“Let’s do the kinetic energy piece T. That’d be the average of galaxy mass m times v²/2 for each galaxy. But we don’t know the masses. For that matter, the potential energy piece, V=G·M·m/R, also needs galaxy mass.”

“If you divide each piece by m you get specific energy, joules/kilogram of galaxy. That’s the same as (km/s)². Does that help?”

“Cool. So have Old Reliable calculate v²/2 for each galaxy, then take the average.”

“We get 208,448 J/kg, which is too many significant figures but never mind. Now what?”

“Twice T would be 416,896 which the Virial Theorem says equals the specific potential energy. That’d be Newton’s G times the cluster mass M divided by the average distance R. Wait, we don’t know M but we do know everything else so we can find M. And dividing that by the galaxy count would be average mass per galaxy. So take the average of all the R distances, times the 416,896 number, and divide that by G.”

“What units do you want G in?”

“Mmm… To cancel the units right we need J/kg times parsecs over … can we do solar masses? That’d be easier to think about than kilograms.”

“Old Reliable says G = 4.3×10^-3 (J/kg)·pc/M_ʘ. Also, the average R is … 890,751 parsecs. Calculating M=v²·R/G … says M is about 90 trillion solar masses. With 29 galaxies the average is around 3 trillion solar masses give or take a couple of factors of 2 or so.”

“But that’s a crazy number, Mr Moire. The Milky Way only has 100 billion stars.”

“Sometimes when the numbers are crazy, we’ve done something wrong. Sometimes the numbers tell us something. These numbers mutter ‘dark matter‘ but in the 1930s only Fritz Zwicky was listening.”

~~ Rich Olcott

Thanks again to Dr KaChun Yu for pointing out Sinclair Smith’s 1936 paper. Naturally, any errors in this post are my own.

A Fleeting Shadowed Sky

On July 8, 2024November 27, 2025 By rolcottIn Astronomy: Planetary Science, Chemistry, UncategorizedLeave a comment

“Hey, Uncle Sy, I’ve got a what‑if for you.”

“What’s that, Teena?”

“Suppose we switched Earth’s air molecules with helium. No, wait, except for the oxygen molecules. I know we need them.”

“First off, a helium-oxygen atmosphere wouldn’t last very long, not on the geological time scale. That’s an unstable situation.”

“Why, would the helium burn up like I’ve seen hydrogen do?”

“No, helium doesn’t burn. Helium atoms are smug. They’re happy with exactly the electrons they have. They don’t give, take or share electrons with oxygen or anything else. No, the issue is that helium’s so light.”

“What difference does that make?”

“The oxygen and helium won’t stay mixed together.”

“The air’s oxygen and nitrogen molecules are all mixed together. They told us that in Science class.”

“That’s correct. But oxygen and nitrogen molecules weigh nearly the same. It would take eight balloon‑fulls of helium to match the weight of one balloon‑full of oxygens. Suppose you had a bunch of equal‑weighted marbles, say red ones and blue ones. Pretend you pour them into a big bucket and stir them around like an atmosphere does. Which color would wind up on top?”

“Both, they’d stay mixed together.”

“Uh-huh. Now replace the blue marbles with marble‑sized ping‑pong balls and stir well.”

“The heavy marbles slide to the bottom. The light balls need to be somewhere so they get bullied up to the top.”

“Exactly. That’s what the oxygen molecules would do — sink down toward the ground and shove the helium atoms up to the top of the atmosphere. Funny thing though — the shoving happens faster than the sinking.”

“Why’s that?”

“It’s the mass thing again. At any given temperature, helium atoms in a gas zip around four times faster than oxygen molecules do. Anyway, the helium atoms that arrive up top won’t stay there.”

“Where else would they go?”

“Anywhere else, basically. Have you heard the phrase, ‘escape velocity‘?”

“It has something to do with rockets, doesn’t it?”

“Well, them, too. The general idea is that once you reach a certain threshold speed relative to a planet or something, you’re going too fast for its gravity to pull you back down. There’s a formula for calculating the speed. The fun thing is, the speed depends on the mass of what you’re escaping from and your distance from the object’s center, but it doesn’t depend on your own mass. It applies to everything from rockets to gas molecules.”

“And we were just talking about helium being zippy. Is it zippy enough to escape Earth?”

“Good thinking! That’s exactly where I was going. The answer is, ‘Maybe.’ It depends on temperature. Warm molecules are zippy, cold molecules not so much. At the same temperature, light molecules are zippier than heavy ones. There’s a chart that shows thresholds for different molecules escaping from different planets. Earth could hold onto its helium atoms, but only if our atmosphere were more than a hundred degrees colder than it is. Warm as we are, bye‑bye helium.”

“How long would that take?”

“That’s a complicated question with lots of ‘It depends’ in the answer. Probably the most important has to do with water.”

“I didn’t say anything about water, just helium and oxygen.”

“I know, but much of Earth’s weather is driven by water vaporizing or condensing or just carrying heat from place to place. Water‑powered hurricanes and even big thunderstorms stir up the atmosphere enough to swoosh helium up to bye‑bye territory. On the other hand, suppose our helium‑Earth is dry. The atmosphere’s layers would be mostly stable, light atoms would be slow to rise. We’d have a very odd‑looking sky.”

“No clouds.”

“Pretty much. But it wouldn’t be blue, either.”

“Would it be pink? I like pink.”

“Sorry, sweetie, it’d be dark dark blue, some lighter near the horizon. Light going past an atomic or molecular particle can scatter from its temporarily distorted electron cloud. Nitrogen and oxygen molecules distort more easily than helium atoms do. Earth skies are blue thanks to sunlight scattered by oxygen and nitrogen. Helium skies wouldn’t have much of that.”

~ Rich Olcott

Thanks again to Xander, who asked a really good helium question.

Cal’s Gallery

On May 20, 2024November 30, 2025 By rolcottIn Astronomy: Techniques, Physics: Black Holes and Relativity, UncategorizedLeave a comment

“Goodness, Cal, you’ve redone your interior decorations.”

“I got tired of looking at the blank wall opposite the cash register, Sy. Check out the gallery. Way at the end here’s the earliest one I’ve got, goes back to 2005.”

“Yeah, ray-marching each background pixel as it passed through the distorting gravity field. That was heavy-duty computer graphics back then.”

“Here’s another one from a year later. I like it better because you can pair up stars and stuff that show up on both sides of the Einstein ring.”

“This one’s famous, comin’ from the Interstellar movie. Funny, I can’t think of any black hole pictures before Interstellar that paid much attention to the accretion disk.”

“There certainly was a lot of that in the specialist literature, but you’re probably right for what leaked out to the pop‑sci press. Most of the published imagery was about how the gravity field distorts the figures behind it. That perpendicular handle was certainly a surprise.”

“This one’s famous, too. It shows what made the first good evidence that black holes are a thing, back in 1965. That ball to the right is a blue supergiant. See how its solar wind is feeding into X-1’s accretion disk? NASA’s picture is from 2017 so it’s not really historical or anything.”

“Now this one is historical, Cal. That image was released in 2019 from data collected in 2017.”

“I knew you’d recognize it, Sy. You’ve written about it enough.”

<sly grin> “Whaddya think of this one, Sy, the gravitational waves from those two black holes that LIGO told us about?”

“You knew I wouldn’t like it.”

“*The final waltz of two black holes*” – **click for video**
Credit: R. Hurt – Caltech / JPL

“It’s just another trampoline picture, right?”

“No, it’s worse than that. Gravitational waves travel at lightspeed. Massive objects like people and 30‑solar‑mass black holes can’t get up to a fraction of a percent of lightspeed without expending an enormous amount of energy. The waves travel outward much faster than objects can orbit each other, even up to the end. Those waves winding outward should be nearly straight.”

“Whoa, Cal, this one isn’t a poster, it’s a monitor screen.”

“I bought a new bigger flat‑screen for home so I brought the old small one here for videos. I like how this movie shows the complicated shape flattening out when you get above the disk. The Interstellar movie made everyone think the disk is some weird double‑handled ring but the handle’s aren’t really there.”

“Mm‑hm, very nice gravity‑lens demonstration. Notice how the ring’s bright in whichever side’s coming toward us whether we’re above or below it?”

“Circling over a black hole structure” — Click for video
Credit: NASA’s Goddard Space Flight Center/Jeremy Schnittman

“No, I hadn’t. Cool. How come?”

“It’s called relativistic Doppler beaming. Time distortion is significant in the close‑in parts of the ring. That affects how we see the flow. In the hole’s frame of reference the brightness and rotation speed are the same all around. In our frame the moving‑closer particles look brighter because they emit more photons per unit of our time. Another one of those unexpected phenomena where physicists say, ‘Of course!’ as soon as they see it but not before.”

~~ Rich Olcott

The Ultimate Pinhole Camera

On May 13, 2024November 30, 2025 By rolcottIn Astronomy: Techniques, Physics: Black Holes and Relativity, UncategorizedLeave a comment

Neither Kareem nor I are much for starting conversations. We’re more the responder type so the poker hands we dealt went pretty quickly. Cathleen had a topic, though. “Speaking of black holes and polarized radio waves, I just read a paper claiming to have developed a 3‑dimensional movie of an event wider than Mercury’s orbit, all from the flickering of a single pixel.”

Eddie bets big, for him. Ten chips. “That’s a lot to ask from just a dot. And what’s polarization got to do with it?”

Cal folds but pipes up anyway. “What was the event?”

“You know Sagittarius A*, the supermassive black hole in the middle of our galaxy?”

“Yeah, one of those orange‑ring pictures.”

“Mm‑hm. Based on radio‑wave emissions from its accretion disk. That image came from a 2‑day Event Horizon Telescope study in 2017. Well, four days after that data was taken, the Chandra satellite observatory saw an X‑ray flare from the same region. The ALMA radio telescope team immediately checked the location. ALMA has excellent signal‑to‑noise and time‑resolution capabilities but it’s only one observatory, not world‑wide like the EHT. The EHT can resolve objects a hundred thousand times closer together than ALMA’s limit. But the team did a lot with what they had.”

Vinnie tends to bet big, maybe because he’s always skeptical. Fifteen chips. “You said ‘claiming‘ like there’s doubt. People don’t trust the data?”

“In science there’s always doubt. In this case, no‑one doubts the data — ALMA’s been providing good observations for over a decade. The doubt’s in the completely new AI‑driven data reduction technique the team used. Is what they did valid? Could their results have been affected by a ‘hallucination’ bug?”

Vinnie doesn’t let go. “What did they do, what have people been doing, and what’s hallucination?”

Susan reluctantly shoves fifteen chips into the pot. “Hallucination is an AI making up stuff. I just encountered that in a paper I’m reviewing. There’s a long paragraph that starts off okay but midway it goes off on a tangent quoting numbers that aren’t in the data. I don’t believe the submitting authors even read what they sent in.”

Kareem drops out of the betting but stays in the conversation. “For a lot of science, curve‑fitting’s a standard practice. You optimize a model’s parameters against measured data. X‑ray crystallography, for example. The atoms in a good crystal are arranged in a regular lattice, right? We send a narrow beam of X‑rays at the crystal and record the intensity reflected at hundreds of angles by the atoms in different lattice planes. Inside the computer we build a parameterized model of the crystal where the parameters are the x‑, y‑ and z‑coordinates of each atom. We have computer routines that convert a given set of configuration parameters into predicted reflection intensity at each observation angle. Curve‑fitting programs cycle through the routines, adjusting parameters until the predictions match the experimental data. The final parameter values give us the atomic structure of the crystal.”

“There’s a lot of that in astrophysics and cosmology, too. This new AI technique stands that strategy on its head. The researchers started with well‑understood physics outside of the event horizon — hot rotating accretion disk, strong magnetic field mostly perpendicular to that, spacetime distortion thanks to General Relativity — and built 50,000 in‑computer examples of what that would look like from a distance.”

“Why so many?”

“The examples had to cover one or two supposed flares of different sizes and brightness at different points in their orbits, plus noise from the accretion disk’s radiation, all from a range of viewpoint angles. Mind you, each example’s only output was a single signal intensity and polarization angle (that’s two dimensions) for that specific set of disk and flare configuration parameters. The team used the example suite to train an AI specialized for assembling 2‑dimensional visual data into a 3‑dimensional model. The AI identified significant patterns in those 50,000 simulated signals. Then the team confronted the trained AI with 100 minutes of real single‑pixel data. It generated this…”

Click through to video, from Levis, *et al*.

“Curve‑fitting but we don’t know the curves!”

“True, Sy, but the AI does.”

“Maybe.”

~ Rich Olcott

Hard Science Ain't Hard

Category: Astronomy

The Not-so-dangerous Banana

EROs Atop A Ladder

One Step After Another

A Big Purple Snowball

To Fly on Another World

The Ideal Gas Game

A Virial Homework Problem

A Fleeting Shadowed Sky

Cal’s Gallery

The Ultimate Pinhole Camera