Category: Physics: Light and Relativity

Speed Limit

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

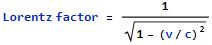
“Wait, Sy, there’s something funny about that Lorentz factor. I’m riding my satellite and you’re in your spaceship to Mars and we compare notes and get different times and lengths and masses and all so we have to use the Lorentz factor to correct numbers between us. Which velocity do we use, yours or mine?”

“Good question, Vinnie. We use the difference between our two frames. We can subtract either velocity from the other one and replace v with that number. Strictly speaking, we’d subtract velocity components perpendicular to the vector between us. If I were to try to land on your satellite I’d have to expend fuel and energy to change my frame’s velocity to yours. When we matched frames the velocity difference would be zero, the Lorentz factor would be 1.0 and I’d see your solar array as a perfect 10×10‑meter square. Our clocks would tick in sync, too.”

“OK, now there’s another thing. That Lorentz formula compares our subtracted speeds to lightspeed c. What do we subtract to get c?”

“Deep question. That’s one of Einstein’s big insights. Suppose from my Mars‑bound spaceship I send out one light pulse toward Mars and another one in the reverse direction, and you’re watching from your satellite. No matter how fast my ship is traveling, Einstein said that you’d see both pulses, forward and backward, traveling at the same speed, c.”

“Wait, shouldn’t that be that your speed gets added to one pulse and subtracted from the other one?”

“Ejected mass works that way, but light has no mass. It measures its speed relative to space itself. What you subtract from c is zero. Everywhere.”

“OK, that’s deep. <pause> But another ‘nother thing—”

“For a guy who doesn’t like equations, you’re really getting into this one.”

“Yeah, as I get up to speed it grows on me. HAW!”

“Nice one, you got me. What’s the ‘nother thing?”

“I remembered how velocity is speed and direction but we’ve been mixing them together. If my satellite’s headed east and your spaceship’s headed west, one of us is minus to the other, right? We’re gonna figure opposite v‑numbers. How’s that work out?”

“You’re right. Makes no difference to the Lorentz factor because the square of a negative difference is the same as the square of its positive twin. You bring up an important point, though — the factor applies to both of us. From my frame, your clock is running slow. From your frame, mine’s the slow one. Einstein’s logic says we’re both right.”

“So we both show the same wrong time, no problem.”

“Nope, you see my clock running slow relative to your clock. I see exactly the reverse. But it gets worse. How about getting your pizza before you order it?”

“Eddie’s good, he ain’t that good. How do you propose to make that happen?”

“Well, I don’t, but follow me here. <working numbers on Old Reliable> Suppose we’re both in spaceships. I’m loafing along at 0.75c relative to Eddie’s pizza place on Earth and your ship is doing 3c. Also, suppose that we can transmit messages and mass much faster than lightspeed.”

“Like those Star Trek transporters and subspace radios.”

“Right. OK, at noon on my personal clock you tell me you’ve ordered pizza so I get one, too. Eddie slaps both our pizzas into his transporter 10 minutes later. The math works out that according to my clock you get your pizza 8.9 minutes before you put in your order. You like that?”

“Gimme a sec … nah, I don’t think so. If I read that formula right with v1 being you and v2 being me, if you run that formula for what I’d see with my velocity on the bottom, that’s a square root of a minus which can’t be right.”

“Yup, the calculation gives an imaginary number, 4.4i minutes, whatever that means. So between us we have two results that are just nonsense — I see effect before cause and you see a ridiculous time. To avoid that sort of thing, Einstein set his speed limit for light, gravity and information.”

“I’m willing to keep under it if you are.”

“Deal.”

~~ Rich Olcott

The Relativity Factor

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Sy, it’s nice that Einstein agreed with Rayleigh’s wave theory stuff but why’d you even drag him in? I thought the faster‑than‑light thing was settled.”

“Vinnie, faster‑than‑light wasn’t even an issue until Einstein came along. Science had known lightspeed was fast but not infinite since Rømer measured it in Newton’s day. ‘Pretty fast,’ they said, but Newtonian mechanics is perfectly happy with any speed you like. Then along came Einstein.”

“Speed cop, was he?”

“Funny, Vinnie. No, Einstein showed that the Universe enforces the lightspeed limit. It’s central to how the Universe works. Come to think of it, the crucial equation had been around for two decades, but it took Einstein to recognize its significance.”

“Ah, geez, equations again.”

“Just this one and it’s simple. It’s all about comparing v for velocity which is how fast something’s going, to c the speed of light. Nothing mystical about the arithmetic — if you’re going half the speed of light, the factor works out to 1.16. Ninety‑nine percent of c gives you 7.09. Tack on another 9 and you’re up to 22.37 and so on.”

“You got those numbers memorized?”

“Mm-hm, they come in handy sometimes.”

“Handy how? What earthly use is it? Nothing around here goes near that fast.”

“Do you like your GPS? It’d be useless if the Lorentz factor weren’t included in the calculations. The satellites that send us their sync signals have an orbit about 84 000 kilometers wide. They run that circle once a sidereal day, just shy of 86 400 seconds. That works out to 3 kilometers per second and a Lorentz factor of 1.000 005.”

“Yeah, so? That’s pretty close to 1.0.”

“It’s off by 5 parts per million. Five parts per million of Earth’s 25 000-mile circumference is an eighth of a mile. Would you be happy if your GPS directed you to somewhere a block away from your address?”

“Depends on why I’m going there, but I get your point. So where else does this factor come into play?”

“Practically anywhere that involves a precision measurement of length or duration. It’s at the core of Einstein’s Special Relativity work. He thought about observing a distant moving object. It’s carrying a clock and a ruler pointed along the direction of motion. The observer would see ticks of the clock get further apart by the Lorentz factor, that’s time dilation. Meanwhile, they’d see the ruler shrink by the factor’s inverse, that’s space compression.”

“What’s this ‘distant observer‘ business?”

“It’s less to do with distance than with inertial frames. If you’re riding one inertial frame with a GPS satellite, you and your clock stay nicely synchronized with the satellite’s signals. You’d measure its 1×1‑meter solar array as a perfect square. Suppose I’m riding a spaceship that’s coasting to Mars. I measure everything relative to my own inertial frame which is different from yours. With my telescope I’d measure your satellite’s solar array as a rectangle, not a square. The side perpendicular to the satellite’s orbit would register the expected 1 meter high, but the side pointing along the orbit would be shorter, 1 meter divided by the Lorentz factor for our velocity difference. Also, our clocks would drift apart by that Lorentz factor.”

“Wait, Sy, there’s something funny about that equation.”

“Oh? What’s funny?”

“What if somebody’s speed gets to c? That’d make the bottom part zero. They didn’t let us do that in school.”

“And they shouldn’t — the answer is infinity. Einstein spotted the same issue but to him it was a feature, not a bug. Take mass, for instance. When they meet Einstein’s famous E=mc² equation most people think of the nuclear energy coming from a stationary lump of uranium. Newton’s F=ma defined mass in terms of a body’s inertia — the greater the mass, the more force needed to achieve a certain amount of acceleration. Einstein recognized that his equation’s ‘E‘ should include energy of motion, the ½mv² kind. He had to adjust ‘m‘ to keep F=ma working properly. The adjustment was to replace inertial mass with ‘relativistic mass,’ calculated as inertial mass times the Lorentz factor. It’d take infinite force to accelerate any relativistic mass up to c. That’s why lightspeed’s the speed limit.”

~~ Rich Olcott

Three-speed Transmission

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Have I got this straight, Sy? You’re saying that prisms throw rainbows because light goes slower through glass than in air and that bends the beam, but every frequency lightwave bends a different amount. Also you’re saying all the bending happens when speeds switch at the glass face, not inside the glass. Am I right so far?”

“Perfect, Vinnie, but you skipped an important detail.”

“Which one?”

“Snell’s ‘index of refraction‘, the ratio of wave speed in vacuum to wave speed in the medium. The higher the frequency, the higher the speed in the medium so the index decreases towards 1.0. The definition lets us calculate wave speed in the medium from that frequency’s refraction index. For most materials the index is usually greater than 1.0, meaning that the speed inside the material is usually slower than in space.”

“Still using those ‘most‘ and ‘usually‘ weasel‑words.”

“Guilty as charged, because we’ve finally gotten to the ‘multiple speeds of light‘ thing. Which means I need more precise wording. The wave speed we’ve been talking about so far applies to a specific part of the wave, say the peak or trough. Those are wave phases, so I’m going to call that speed the ‘phase speed‘, OK?”

“Fine with me.”

“Good, because the second speed is different. Among his many important contributions, Lord Rayleigh pointed out that you can’t have a pulse that’s one pure frequency. A single‑frequency wave never starts and never ends. Do you remember the time I combined waves to draw a camel?”

“You did, mostly, but there was funny stuff at his nose and butt.”

“Because I only included about a hundred component waves. It’d take many more to kill those boundary zig‑zags. Any finite wave has the same issue. Rayleigh said that an individual wave has a phase speed, but any ‘peculiarity,’ like a pulse rise or fall, could only be created by a group of waves. The peculiarity could travel at a different speed from the component waves, like a pair of scissors where the cutting point moves faster than either blade.”

“Sounds like carrier wave and sidebands on my ham radio. But if different frequencies have different speeds they’d get all out of sync with each other. How does a photon stay in one piece?”

“The vacuum is non-dispersive — the photon’s component waves all travel at the same speed and stay together. If a medium absorbs some frequency, that makes it dispersive and that changes things.”

“Ah, that’s why you hedged about transparency.”

“Exactly. Throw in a few absorbing atoms, like cobalt that absorbs red or gold that absorbs blue, and you get interesting effects from your sideband components interacting. Skipping some math, the bottom line is simple and cute. The group speed’s equation is just like the phase speed’s except there’s a positive or negative correction term in the denominator.”

“Sy, I don’t like equations, remember? I suppose f is frequency in your correction term but what’s slope?”

“That’s a measure of how rapidly the index changes as the frequency changes. For most frequencies and most media, the slope is very slightly negative because the index slowly descends towards 1.0 at high energies. The vg fraction’s denominator stays just less than nf so the group goes slightly faster than the phase. Near an absorption line, though, things get sloppy. Waves that are just a little off the absorber’s favorite frequency can still interact with it. That changes their speed and the ‘corrected’ refraction index.”

“Gimme a sec … guess I’m OK with the positive slopes but there’s that yellow part where the slope is negative. Wouldn’t that make the fraction’s bottom smaller and the group speed higher?”

“Certainly. In fact, under the right conditions the denominator can be less than 1.0. That pushes the group speed above c — faster than light in vacuum, even though the component waves all run slower than vacuum lightspeed. It’s only the between‑component out‑of‑syncness relationship that scissors along beyond c.”

“You said there’s a third speed?”

“Signals. In a dispersive medium those sideband waves get chaotic and can’t carry information. Wave theory and Einstein agree — chaos may be able to travel faster than light, but information can’t.”

~~ Rich Olcott

Chasing Rainbows

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“C’mon, Sy, Newton gets three cheers for tying numbers to the rainbow’s colors and all that, but what’s it got to do with that three speeds of light thing which is where we started this discussion?”

“Vinnie, they weren’t just numbers, they were angles. The puzzle was why each color was bent to a different degree when entering or leaving the prism. That was an inconvenient truth for Newton.”

“Inconvenient? There’s a loaded word.”

“Indeed. A little context — Newton was in a big brouhaha about whether light was particles or waves. Newton was a particle guy all the way, battling wave theory proponents like Euler and Descartes and their followers on the Continent. Even Hooke in London had a wave theory. Newton’s problem was that his beam deflections happened right at the prism’s air‑glass interfaces.”

“What difference does that … wait, you mean that there’s no bending inside the prism? Light inside still goes straight but in a different direction?”

“That’s it, exactly. The deflection angles are the same, whether the beam hits the prism near the short‑path tip or the long‑path base. No evidence of further deviation inside the prism unless it has bubbles — Newton had to discard or mask off some bad prisms. Explaining the no‑curvature behavior is difficult in a particle framework, easy in a wave framework.”

“Really? I don’t see why.”

Left: faster medium, right: slower medium
Credit: Ulflund, under Creative Commons 1.0

“Suppose light is particles, which by definition are local things affected only by local forces. The medium’s effects on a particle would happen in the bulk material rather than at the interface. The effect would accumulate as the particles travel further through the medium. The bend should be a curve. Unfortunately for Newton, that’s not what his observations showed.”

“OK, scratch particles. Why not scratch waves, too?”

“Waves have no problem with abrupt variation at an interface, They flip immediately to a new stable mode. For example. here’s an animation showing an abrupt speed change at the interface between a fast‑travel medium like air and a slow‑travel medium like glass or water. See how one end of each bar gets slowed down while the other end is still moving at speed? By the time the whole bar is inside, its path has slewed to the refraction angle.”

“Like a car sliding on ice when a rear wheel sticks for an moment, eh Sy?”

“That was not a fun ride, Vinnie.”

“I enjoyed it. Whatever, I get how going air‑to‑glass or vice‑versa can change a beam’s direction. But if everything’s going through the same angle, how do rainbows happen?”

“Everything doesn’t go through the same angle. Frequencies make a difference. Go back to the video and keep your eye on one bar as it sweeps up the interface. See how the sweep’s speed controls the deflection angle?”

“Yeah, if the sweep went slower the beam would get a chance to bend further. Faster sweeps would bend it less. But what could change the sweep speed?

“Two things. One, change the medium to one with a different transmission speed. Two, change the wave itself so it has a different speed. According to Snell’s Law, the important parameter for a pair of media is their ratio of fast‑speed divided by slow‑speed. If the fast medium is a vacuum that ratio is the slow medium’s index of refraction. The greater the index, the greater the bend.”

“Changing the medium doesn’t apply. I got one prism, it’s got one index, but I still get a whole rainbow.”

“Right, rainbows are about how one prism treats a bunch of waves with different time and space frequencies.”

“Space frequency?”

“If you measure a wave in meters it’s cycles per meter.”

“Wavelength upside down. Got it.”

“Whether you figure in frequencies or intervals, the wave speed works out the same.”

“Speed of light, finally.”

“Point is, when a wave goes through any medium, its time frequency doesn’t change but its space frequency does. Interaction with local charge shortens the wavelength. Short‑wavelength blue waves are held back more than long‑wavelength red ones. The different angles make your rainbow. The hold‑back is why refraction indices are usually greater than one.”

“Usually?”

~~ Rich Olcott

Through A Prism Brightly

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

Familiar footsteps outside my office. “C’mon in, Vinnie, the door’s open.”

“Hi, Sy, gotta minute?”

“Sure, Vinnie, business is slow. What’s up?”

“Business is slow for me, too. I was looking over some of your old posts—”

“That slow, eh?”

“You know it. Anyway, I’m hung up on that video where light’s got two different speeds.”

“Three, really.”

“That’s even worse. What’s the story?”

“Well, first thing, it depends on where the light is. If you’re out in the vacuum, far away from atoms, they’re all the same, c. Simple.”

“Matter messes things up, then.”

“Of course. Our familiar kind of matter, anyway, made of charges like quarks and electrons. Light’s whole job is to interact with charges. When it does, things happen.”

“Sure — photon bangs into a rock, it stops.”

“It’s not that simple. Remember the wave-particle craziness? Light’s a particle at either end of its trip but in between it’s a wave. The wave could reflect off the rock or diffract around it. Interstellar infra-red astronomy depends upon IR scooting around dust particles so we can see the stars behind the dust clouds. What gets interesting is when the light encounters a mostly transparent medium.”

“I get suspicious when you emphasize ‘mostly.’ Mostly how?”

“Transparent means no absorption. The only thing that’s completely transparent is empty space. Anything made of normal matter can’t be completely transparent, because every kind of atom absorbs certain frequencies.”

“Glass is transparent.”

“To visible light, but even that depends on the glass. Ever notice how cheap drinking glasses have a greenish tint when you look down at the rim? Some light absorption, just not very much. Even pure silica glass is opaque beyond the near ultraviolet. … Okay, bear with me on this. Why do you suppose Newton made such a fuss about prisms?”

“Because he saw it made a rainbow in sunlight and thought that was pretty?”

“Nothing so mild. We’re talking Newton here. No, it had to do with one of his famous ‘I’m right and everyone else is wrong‘ battles. Aristotle said that sunlight is pure white‑color, and that objects emit various kinds of darkness to overcome the white and produce colors for us. That was academic gospel for 2000 years until Newton decided it was wrong. He went to war with Aristotle using prisms as his primary weapons.”

“So that’s why he invented them?”

“No, no, they’d been around for millennia, ever since humans discovered that prismatic quartz crystals in a beam of sunlight throw rainbows. Newton’s innovation was to use multiple prisms arrayed with lenses and mirrors. His most direct attack on Aristotle used two prisms. He aimed the beam coming out of the first prism onto a reversed second prism. Except for some red and violet fringes at the edges, the light coming out of the second prism matched the original sunlight beam. That proved colors are in the light, not in Aristotle’s darknesses.”

“Newton won. End of story.”

“Not by a long shot. Aristotle had the strength of tradition behind him. A lot of Continental academics and churchmen had built their careers around his works. Newton’s earlier battles had won him many enemies and some grudging respect but few effective allies. Worse, Newton published his experiments and observations in a treatise which he wrote in English instead of the conventional scholarly Latin. Typical Newtonian belligerence, probably. The French academicians reacted by simply rejecting his claims out of hand. It took a generational turnover before his thinking was widely accepted.”

“Where do speeds come into this?”

“Through another experiment in Newton’s Optics treatise. If he used a card with a hole in it to isolate, say, green light in the space between the two prisms, the light beam coming from the second prism was the matching green. No evidence of any other colors. That was an important observation on its own, but Newton’s real genius move was to measure the diffraction angles. Every color had its own angle. No matter the conditions, any particular light color was always bent by the same number of degrees. Newton had put numbers to colors. That laid the groundwork for all of spectroscopic science.”

“And that ties to speed how?”

~~ Rich Olcott

‘Twixt A Rock And A Vortex

On By rolcottIn Physics: Gaps, Physics: Light and Relativity, Physics: Newton and Gravity, UncategorizedLeave a comment

A chilly late December walk in the park and there’s Vinnie on a lakeside bench, staring at the geese and looking morose. “Hi, Vinnie, why so down on such a bright day?”

“Hi, Sy. I guess you ain’t heard. Frankie’s got the ‘rona.”

“Frankie??!? The guys got the constitution of an ox. I don’t think he’s ever been sick in his life.”

“Probably not. Remember when that bug going around last January had everyone coughing for a week? Passed him right by. This time’s different. Three days after he showed a fever, bang, he’s in the hospital.”

“Wow. How’s Emma?”

“She had it first — a week of headaches and coughing. She’s OK now but worried sick. Hospital won’t let her in to see him, of course, which is a good thing I suppose so she can stay home with the kids and their schoolwork.”

“Bummer. We knew it was coming but…”

“Yeah. Makes a difference when it’s someone you know. Hey, do me a favor — throw some science at me, get my mind off this for a while.”

“That’s a big assignment, considering. Let’s see … patient, pandemic … Ah! E pluribus unum and back again.”

“Come again?”

“One of the gaps that stand between Physics and being an exact science.”

“I thought Physics was exact.”

“Good to fifteen decimal places in a few special experiments, but hardly exact. There’s many a slip ‘twixt theory and practice. One of the slips is the gap between kinematic physics, about how separate objects interact, and continuum physics, where you’re looking at one big thing.”

“This is sounding like that Loschmidt guy again.”

“It’s related but bigger. Newton worked on both sides of this one. On the kinematics side there’s billiard balls and planets and such. Assuming no frictional energy loss, Newton’s Three Laws and his Law of Gravity let us calculate exact predictions for their future trajectories … unless you’ve got more than three objects in play. It’s mathematically impossible to write exact predictions for four or more objects unless they start in one of a few special configurations. Newton didn’t do atoms, no surprise, but his work led to Schrödinger’s equation for an exact description of single electron, single nucleus systems. Anything more complicated, all we can do is approximate.”

“Computers. They do a lot with computers.”

“True, but that’s still approximating. Time‑step by time‑step and you never know what might sneak in or out between steps.”

“What’s ‘continuum‘ about then? Q on Star trek?”

“Hardly, we’re talking predictability here. Q’s thing is unpredictability. A physics continuum is a solid or fluid with no relevant internal structure, just an unbroken mass from one edge to the other. Newton showed how to analyze a continuum’s smooth churning by considering the forces that act on an imaginary isolated packet of stuff at various points in there. He basically invented the idea of viscosity as a way to account for friction between a fluid and the walls of the pipe it’s flowing through.”

“Smooth churning, eh? I see a problem.”

“What’s that?”

“The eddies and whirlpools I see when I row — not smooth.”

“Good point. In fact, that’s the point I was getting to. We can use extensions of Newton’s technique to handle a single well‑behaved whirlpool, but in real life big whirlpools throw off smaller ones and they spawn eddies and mini‑vortices and so on, all the way down to atom level. That turns out to be another intractable calculation, just as impossible as the many‑body particle mechanics problem.”

“Ah‑hah! That’s the gap! Newton just did the simple stuff at both ends, stayed away from the middle where things get complicated.”

“Exactly. To his credit, though, he pointed the way for the rest of us.”

“So how can you handle the middle?”

“The same thing that quantum mechanics does — use statistics. That’s if the math expressions are average‑able which sometimes they’re not, and if statistical numbers are good enough for why you’re doing the calculation. Not good enough for weather prediction, for instance — climate is about averages but weather needs specifics.”

“Yeah, like it’s just started to snow which I wasn’t expecting. I’m heading home. See ya, Sy.”

“See ya, Vinnie. … Frankie. … Geez.“

~~ Rich Olcott

To Swerve And Project

On By rolcottIn Astronomy: Planetary Science, Physics: Light and Relativity, UncategorizedLeave a comment

A crisp Fall dawn, crisp fallen leaves under my feet as I jog the path by the park’s lake.

“Hey! Moire! How about these red sunrises and sunsets? Remind you of Mars?”

“Morning, Mr Feder. Not much, and definitely not dawn or dusk. Those tend more to blue, as a matter of fact.”

“Waitaminnit, Moire. I seen that Brad Pitt Martian movie, him driving hisself all alone across that big plain — the place is blood‑red.”

“Think a minute, Mr Feder. If he was all alone, who was running the cameras?”

“Uhhh, right. Movie. Yeah, they were really on Earth so they could director the lighting and all. But they said they’d scienced the … heck out of it.”

“Oh they did, better than most movies, but artistic license took over in a couple of places. People expect Mars to be red, not mostly clay colored like it really is, so the producers served up red.”

“Wait, I remember the conversation about Earth is blue because of the oceans and Mars is red because of its rusty atmosphere. So what’s with the sky colors?”

“Looking up at sunlight through an atmosphere is very different from looking down at the surface. It all has to do with how what’s in the atmosphere interacts with sunlight. Take Earth’s blue sky, for instance.”

“My favorite color.”

“Sure it is. OK, the Sun’s disk takes up much less than 1% of the sky but that’s enough to give us all our sunlight photons. A fraction of them run into something on the way down to Earth’s surface. What happens depends on how big the something is compared to the photon wavelength. Much larger things, maybe an airplane, completely block the photons and we get a shadow.”

“Obviously.”

“Yeah, but life’s more interesting for smaller somethings. For things like air molecules and dust particles that are much smaller than the the wavelength of visible light, the waves generally swerve around the particle. How much they swerve depends on the wavelength — extreme blue light bends about ten times more than extreme red light for the same scattering particle. So suppose there’s a kid a few miles away from us looking at the sky while we’re looking at it here. There’s a sunbeam with a rainbow‑load of photons headed for the kid, but there are dust particles in the way. Get the picture?”

“Sure, sure, get on with it.”

“So some of the light swerves. The red swerves a little but the blue light swerves ten times as much, enough that it heads straight for us. What color do we see when we look in that direction?”

“Blue, of course.”

“Blue everywhere in the lit‑up sky except when we look straight at the Sun.”

“What about these pretty red sunsets and the red skies over the wildfires?”

“Two different but related phenomena. Sunsets first. An incoming photon with just the right wavelength may simply be absorbed by a molecule. Doesn’t happen often, but there’s lots of molecules. Turns out that oxygen and ozone absorb blue light more strongly than red light. When we’re looking horizontally towards a sunset we’re looking through many more oxygen molecules than when we look vertically. We see the red part of a blue‑filtered version of that swerve rainbow.”

“And the fire skies?”

“The fires released huge amounts of fine smoke particles, just the right size for color‑scattering. Blue light swerves again and again until it’s either absorbed or shot out to space. Red light survives.”

Upper image – Golden Gate Bay under fiery skies, Sept 2020
Lower image – Sunset from Gusev Crater, Mars
Credit: NASA/JPL/Texas A&M/Cornell

“So what’s different about Mars?”

“Three things — Mars dust is different from Earth’s, its atmosphere is a lot thinner, and there’s practically no atmospheric water or oxygen. Rusty Mars dust is the size of smoke particles. With no rain or snow to settle out the dust, it stays aloft all the time. Rust is red because it absorbs blue light and reflects only the red part. With less diffused sunlight, Mars’ sky is basically the black of space overlaid with a red tint. Sunsets are blue‑ish because what blue light there is can travel further.”

“Earth skies are better.”

~~ Rich Olcott

A Far And Dusty Traveler

On By rolcottIn Astronomy: Techniques, Physics: Light and Relativity, UncategorizedLeave a comment

Cathleen takes the mic. “Quick coffee and scone break, folks, then Jim will continue our ‘IR, Spitzer And The Universe‘ symposium.” <pause> “OK, we’re back in business. Jim?”

“Thanks, Cathleen. Well, we’ve discussed finding astronomical molecules with infra-red. Now for a couple of other IR applications. First up — looking at things that are really far away. Everyone here knows that the Universe is expanding, right?”

<general murmur of assent, although the probably-an-Art-major looks startled>

“Great. Because of the expansion, light from a far-away object gets stretched out to longer wavelengths on its way to us. Say a sodium atom shot a brilliant yellow-gold 590-nanometer photon at us, but at the time the atom was 12.5 million lightyears away. By the time that wave reaches us it’s been broadened to 3540 nanometers, comfortably into the infra-red. Distant things are redder, sometimes too red to see with an optical telescope. The Spitzer Space Telescope‘s infra-red optics let us see those reddened photons. And then there’s dust.”

<voice from the crowd> “Dust?”

“Cosmic dust, pretty much all the normal matter that’s not clumped into stars and planets. Some of it is leftovers from early times in the Universe, but much of it is stellar wind. Stars continuously spew particles in their normal day-to-day operation. There’s a lot more of that when one explodes as a nova or supernova. Dust particles come in all sizes but most are smaller than the ones in tobacco smoke.”

<same voice> “If they’re so small, why do we care about them?”

“Two reasons. First, there’s a lot of them. Maybe only a thousand particles per cubic kilometer of space, but there’s a huge number of cubic kilometers in space and they add up. More important is what the dust particles are made of and where we found them. Close inspection of the dust is like doing astronomical archaeology, giving us clues about how stars and galaxies evolved.”

<Vinnie, skeptical as always> “So what’s infra-red got to do with dust?”

“Depends on what kind of astronomy you’re interested in. Dust reflects and emits IR light. Frequency patterns in the light can tell us what that dust made of. On the other hand there’s the way that dust doesn’t interact with infra-red.”

<several voices> “Wait, what?”

The Milky Way from Black Rock Desert NV
By Steve Jurvetson via Flickr, Wikimedia Commons, CC BY 2.0

“If Al’s gotten his video system working … ah, he has and it does. Look at this gorgeous shot of the Milky Way Galaxy. See all the dark areas? That’s dust blocking the visible light. The scattered stars in those areas are simply nearer to us than the clouds. We’d like to study what’s back beyond the clouds, especially near the galaxy’s core. That’s a really interesting region but the clouds block its visible light. Here’s the neat part — the clouds don’t block its infra-red light.”

<other voices> “Huh?” “Why wouldn’t they?”

“It’s the size of the waves versus the size of the particles. Take an extreme case — what’s the wavelength of Earth’s ocean tides?”

<Silence, so I speak up.> “Two high tides a day, so the wavelength is half the Earth’s circumference or about 12’500 miles.”

“Right. Now say you’re at the beach and you’re out there wading and the water’s calm. Would you notice the tide?”

“No, rise or fall would be too gentle to affect me.”

“Now let’s add a swell whose peak-to-peak wavelength is about human-height scale.”

“Whoa, I’d be dragged back and forth as each wave passes.”

“Just for grins, let’s replace that swell with waves the same height but only a millimeter apart. Oh, and you’re wearing SCUBA equipment.”

“Have mercy! Well, I should be able to stand in place because I wouldn’t even feel the peaks and troughs as separate waves, just a foamy massage. Thanks for the breathing assistance, though.”

“You’re welcome, and thanks for helping with the thought experiment. Most cosmic dust particles are less than 100 nanometers across. Infra-red wavelengths run 100 to 1000 times longer than that. Infra-red light from those cloud-hidden stars just curves around particles that can stop visible lightwaves cold. Spitzer Space Telescope and its IR-sensitive kin provide deeper and further views than visible light allows.”

~~ Rich Olcott

Above The Air, Below The Red

On By rolcottIn Astronomy: Multi-messenger, Astronomy: Techniques, Physics: Light and Relativity, UncategorizedLeave a comment

Vinnie and I walk into Al’s coffee shop just as he sets out a tray of scones. “Odd-looking topping on those, Al. What is it?”

“Dark cherry and dark chocolate, Sy. Something about looking infra-red. Cathleen special-ordered them for some Astronomy event she’s hosting in the back room. Carry this tray in there for me?”

Vinne grabs the tray and a scone. “Sure, Al. … Mmm, tasty. … Hi, Cathleen. Here’s your scones. What’s the event?”

“It’s a memorial symposium for the Spitzer Space Telescope, Vinnie. Spitzer‘s been an infra-red workhorse for almost 17 years and NASA formally retired it at the end of January.”

“What’s so special about infra-red? It’s just light, right? We got the Hubble for that.”

“A perfect cue for Jim’s talk. <to crowd> Grab a scone and settle down, everyone. Welcome to our symposium, ‘IR , Spitzer And The Universe.’ Our first presentation today is entitled ‘What’s So Special About Infra-red?‘ Jim, you’re on.”

“Thanks, Cathleen. This is an introductory talk, so I’ll keep it mostly non-technical. So, question for everybody — when you see ‘IR‘, what do you think of first?”

<shouts from the crowd> “Pizza warmer!” “Invisible light!” “Night-vision goggles!”

“Pretty much what I expected. All relevant, but IR’s much more than that. To begin with, many more colors than visible light. We can distinguish colors in the rainbow because each color’s lightwave has a different frequency. Everybody OK with that?”

<general mutter of assent>

“OK. Well, the frequency at the violet end of the visible spectrum is a bit less than double the frequency at the red end. In music when you double the frequency you go up an octave. The range of colors we see from red to violet is less than an octave, about like going from A-natural to F-sharp on the piano. The infra-red spectrum covers almost nine octaves. An 88-key piano doesn’t even do eight.”

<voice from the crowd, maybe an Art major> “Wow, if we could see infra-red think of all the colors there’d be!”

“But you’d need a whole collection of specialized eyes to see them. With light, every time you go down an octave you reduce the photon’s energy capacity by half. Visible light is visible because its photons have just enough energy to cause an electronic change in our retinas’ photoreceptor molecules. Five octaves higher than that, the photons have enough energy to knock electrons right out of a molecule like DNA. An octave lower than visible, almost nothing electronic.”

<Vinnie’s always-skeptical voice> “If there’s no connecting with electrons, how does electronic infra-red detection work?”

“Two ways. A few semiconductor configurations are sensitive to near- and mid-infra-red photons. The Spitzer‘s sensors are grids of those configurations. To handle really low-frequency IR you have to sense heat directly with bolometer techniques that track expansion and contraction.”

<another skeptical voice> “OK then, how does infra-red heating work?”

“Looks like a paradox, doesn’t it? Infra-red photons are too low-energy to make a quantum change in a molecule’s electronic arrangement, but we know that the only way photons can have an effect is by making quantum changes. So how come we feel infra-red’s heat? The key is, photons can interact with any kind of charged structure, not just electrons. If a molecule’s charges aren’t perfectly balanced a photon can vibrate or rotate part of a molecule or even the whole thing. That changes its kinetic energy because molecular motion is heat, right? Fortunately for the astronomers, gas vibrations and rotations are quantized, too. An isolated water molecule can only do stepwise changes in vibration and rotation.”

“Why’s that fortunate?”

“Because that’s how I do my research. Every kind of molecule has its own set of steps, its own set of frequencies where it can absorb light. The infra-red range lets us do for molecules what the visual range lets us do for atoms. By charting specific absorption bands we’ve located and identified interstellar clouds of water, formaldehyde and a host of other chemicals. I just recently saw a report of ‘helonium‘, a molecular ion containing helium and hydrogen, left over from when the Universe began. Infra-red is so cool.”

“No, it’s warm.”

Image suggested by Alex

~~ Rich Olcott

The Sight And Sound of Snow

On By rolcottIn Chemistry, Physics: Light and Relativity, UncategorizedLeave a comment

<ring> “Moire here.”

“Uncle Sy! Uncle Sy! It’s snowing! It’s snowing!”

“Yes, Teena, it started last night after you went to bed. But it’s real early now and I haven’t had breakfast yet. I’ll be over there in a little while and we can do snow stuff.”

“Yaaay! I’ll have breakfast, too. Mommie, can we have oatmeal with raisins?” <click>

<knock, knock> “Uncle Sy! You’re here! I wanna go sledding! Get my sled out, please?”

“G’morning, Sis. G’morning, Teena. Get your snowsuit and boots on, Sweetie. Want to come along, Sis? It’s a cold, dry snow, not much wind.”

“No, I’ll just stay warm and get the hot chocolate ready.”

“Bless you for that, Sis. OK, young’un, ready to go?”

“Ready! Pull me on the sled to the sledding hill, Uncle Sy!”

“Ooo, it’s so quiet. Why’s it always quiet when snow’s falling, Uncle Sy? Is the world holding its breath? And why is snow white? When I hold snow in my hand it melts and then it’s no-color.”

“Always the good questions. Actually, these two are related and they both have to do with the shape of snowflakes. Here, hold out your arm and let’s see if you can catch a few. No, don’t try to chase them, the breeze from your arm will blow them away. Just let them fall onto your arm. That’s right. Now look at them real close.”

“They’re all spiky, not flat and pretty like the ones in my picture book!”

“That’s because they grew fast in a really cold cloud and didn’t have time to develop evenly. You have to work slow to make something that’s really pretty.”

“But if they’re spiky like this they can’t lay down flat together and be cozy!”

“Ah, that’s the key. Fresh spiky snowflakes make fluffy snow, which is why skiers love it. See how the flakes puff into the air when I scuff my boot? Those tiny spikes break off easily and make it easy for a ski to glide over the surface. Your sled, too — you’ve grown so big I’d be hard-put to pull you over wet snow. That fluffiness is why <hushed voice> it’s so quiet now.”

“Shhh … <whispered> yeah … <back to full voice> Wait, how does fluffy make quiet?”

“Because sound waves … Have we talked about sound waves? I guess we haven’t. OK, clap your hands once.”

<CLAP!>

“Good. When your hands came together they pushed away the air molecules that were between them. Those molecules pushed on the next molecules and those pushed on the next ones on and on until they got to your ear and you heard the sound. Make sense?”

“Ye-aa-uh. Is the push-push-push the wave?”

“Exactly. OK, now imagine that a wave hits a wall or some packed-down icy snow. What will happen?”

“It’ll bounce off like my paddle-ball toy!”

“Smart girl. Now imagine that a wave hits fluffy snow.”

“Um … it’ll get all lost bouncing between all the spikes, right?”

“Perfect. That’s exactly what happens. Some of the wave is scattered by falling snowflakes and much of what’s left spreads into the snow on the ground. That doesn’t leave much sound energy for us to hear.”

“You said that snow’s white because of what snow does to sound, but look, it’s so bright I have to squint my eyes!”

“That’s not exactly what I said, I said they’re related. Hmm… ah! You know that ornament your Mommie has hanging in the kitchen window?”

“The fairy holding the glass jewel? Yeah, when the sunlight hits it there’s rainbows all over the room! I love that!”

A beam or white light passing through two prisms. The first produces a spectrum and the second remixes the colors to white.

“I do, too. White light like sunlight has all colors in it and that jewel splits the colors apart so you can see them. Well, suppose that jewel is surrounded by other jewels that can put the colors together again. Here’s a picture on my cellphone for a clue.”

“White goes to rainbow and back to white again … I’ll bet the snowflakes act like little jewels and bounce all the colors around but the light doesn’t get trapped and it comes out and we see the WHITE again! Right?”

“So right that we’re going home for hot chocolate.”

“Yaaay!”

~~ Rich Olcott

PS – A Deeper Look.