Category: Physics: Waves

Trombones And Echoes

On By rolcottIn Physics: Foundations of Measurement, Physics: Waves, UncategorizedLeave a comment

Vinnie’s fiddling with his Pizza Eddie’s pizza crumbs. “Hey, Sy, so we got the time standard switched over from that faked 1900 Sun to counting lightwave peaks in a laser beam. I understand why that’s more precise ’cause it’s a counting measure, and it’s repeatable and portable ’cause they can set up a time laser on Mars or wherever that uses the same identical kinds of atoms to do the frequency stuff. All this talk I hear about spacetime, I’m thinkin’ space is linked to time, right? So are they doing smart stuff like that for measuring space?”

“They did in 1960, Vinnie. Before that the meter was defined to be the distance between two carefully positioned scratches on a platinum-iridium bar that was lovingly preserved in a Paris basement vault. In 1960 they went to a new standard. Here, I’ll bring it up on Old Reliable. By the way, it’s spelled m-e-t-e-r stateside, but it’s the same thing.”

“Mmm… Something goofy there. Look at the number. You’ve been going on about how a counted standard is more precise than one that depends on ratios. How can you count 0.73 of a cycle?”

“You can’t, of course, but suppose you look at 100 meters. Then you’d be looking at an even 165,076,373 of them, OK?”

“Sorta, but now you’re counting 165 million peaks. That’s a lot to ask even a grad student to do, if you can trust him.”

“He won’t have to. Twenty-three years later they went to this better definition.”

“Wait, that depends on how accurate we can measure the speed of light. We get more accurate, the number changes. Doesn’t that get us into the ‘different king, different foot-size’ hassle?”

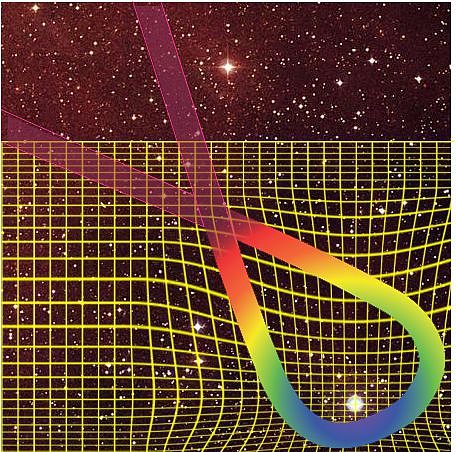
“Quite the contrary. It locks down the size of the unit. Suppose we develop technology that’s good to another half-dozen digits of precision. Then we just tack half-a-dozen zeroes onto that fraction’s denominator after its decimal point. Einstein said that the speed of light is the same everywhere in the Universe. Defining the meter in terms of lightspeed gives us the same kind of good-everywhere metric for space that the atomic clocks give us for time.”

“I suppose, but that doesn’t really get us past that crazy-high count problem.”

“Actually, we’ve got three different strategies for different length scales. For long distances we just use time-of-flight. Pick someplace far away and bounce a laser pulse off of it. Use an atomic clock to measure the round-trip time. Take half that, divide by the defined speed of light and you’ve got the distance in meters. Accuracy is limited only by the clock’s resolution and the pulse’s duration. The Moon’s about a quarter-million miles away which would be about 2½ seconds round-trip. We’ve put reflectors up there that astronomers can track to within a few millimeters.”

“Fine, but when distances get smaller you don’t have as many clock-ticks to work with. Then what do you do?”

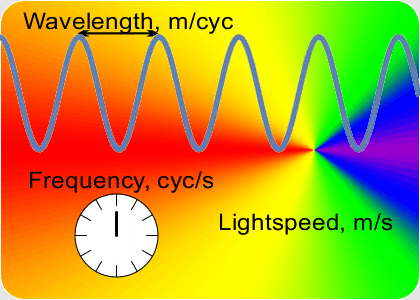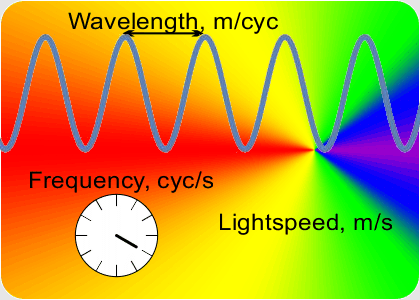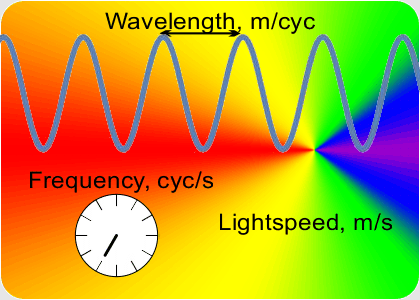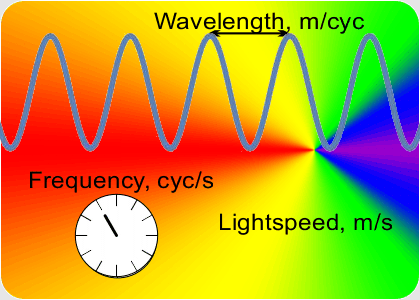
“You go to something that doesn’t depend on clock-ticks but is still connected to that constant speed of light. Here, this video on Old Reliable ought to give you a clue.”

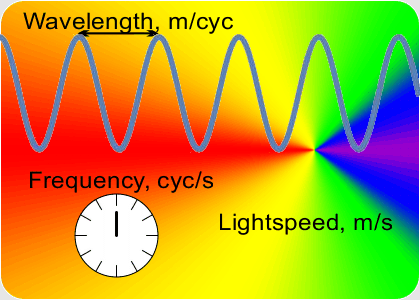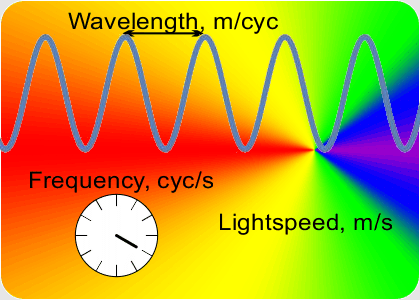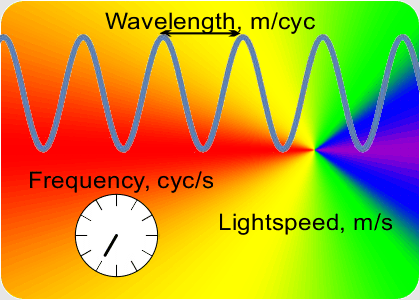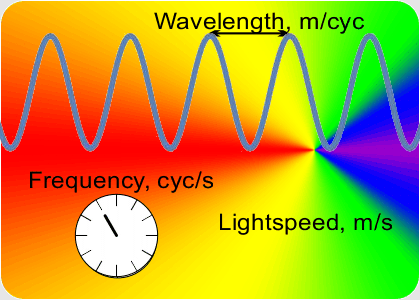
“OK, the speed which is a constant is the number of peaks that’s the frequency times the distance between them that’s the wavelength. If I know a wavelength then arithmetic gets me the frequency and vice-versa. Fine, but how do I get either one of them?”

“How do you tune a trombone?”

“Huh? I suppose you just move the slide until you get the note you want.”

“Yup, if a musician has good ear training and good muscle memory they can set the trombone’s resonant tube length to play the right frequency. Table-top laser distance measurements use the same principle. A laser has a resonant cavity between two mirrors. Setting the mirror-to-mirror distance determines the laser’s output. When you match the cavity length to something you want to measure, the laser beam frequency tells you the distance. At smaller scales you use interference techniques to compare wavelengths.”

Vinnie gets a gleam in his eye. “Time-of-flight measurement, eh?” He flicks a pizza crumb across the room.

In a flash Eddie’s standing over our table. “Hey, hotshot, do that again and you’re outta here!”

“Speed of light, Sy?”

“Pretty close, Vinnie.”

~~ Rich Olcott

A Clock You Can Count On And Vice-versa

On By rolcottIn Physics: Foundations of Measurement, Physics: Waves, UncategorizedLeave a comment

We’re both leery of the Acme Building’s elevators after escaping from one, so Vinnie and I take the stairs down to Pizza Eddie’s. “Faster, Sy, that order we called in will be cold when we get there.”

“Maybe not, Vinnie. Depends on his backlog.”

“Hey, before all this started, we were talking about the improved time standard and you said something about optical clockwork. I gather it’s got something to do with lasers and such.”

“It sure does. Boils down to Science preferring count-based units over ratios because they’re more precise. If you count something twice you should get exactly the same answer each time; if you’re measuring a ratio against a ruler or something, duplicate measurements might not agree. For instance, you can probably tell me how many steps there are between floors — “

“Fourteen”

“— more precisely than you can tell me the floor-to-floor height in feet or meters. And more accurately, too.”

“How can it be more accurate? I’ve got a range-finder gadget that reads out to a tenth of an inch. Or a millimeter if you set the switch for that.”

“Because that reading is subject to all sorts of potential errors — maybe you’re pointing it at an angle, or its temperature calibration is off, or you’re moving and there’s a Doppler effect. It may give you exactly the same reading twice in a row —”

“I always measure twice before I cut once.”

“Of course you do. My point is, that device might give you very precise but inaccurate answers that are way off. You’d have to calibrate its readings against a trustworthy standard to be sure.”

“Suppose my range-finder’s as precise as my step-counting. How can step-counting be better?”

“Because the step is defined as the measurement unit. There’s no calibration issues or instrumental drift or ‘it depends on how good the carpenter was,’ a step is a step. Step counting is accurate by definition. Nearly all our conventional units of measurement have some built-in ‘‘it depends’ factors that drive the measurement folks crazy. Like the foot, for instance — every time a new king came to power, his foot became the new standard and every wood and cloth merchant in the kingdom had to revise their inventory listings.”

“OK, so that’s basically why the time-measurement people wanted to get away from that ‘a second is a fraction of a day back when‘ definition — too many ‘it depends’ factors and they wanted something they could count. Got it. So back in what, 1967? they switched to a time standard where they could count waves and they went to the ‘a second is so many waves‘ thing. I also got that their first shot was to use microwaves ’cause that’s what they could count. But that was half-a-century ago. Haven’t they moved up the spectrum since then, say to visible light?”

“Not quite. They had to get tricky. Think about it. Yellow-orange light’s wavelength is about 600 nanometers or 600×10-9 meters. Divide that by the speed of light, 3×108 meters/second, and you get that each wave whizzes by in only 2×10-15 seconds. Our electronics still can’t count that fast, but we can cheat. Uhhh … which would be easier to answer — how many floors in this building or how many steps?”

“Floors, of course, there’s a lot fewer of them.”

“But the step count would track the floor count, regular as clockwork, because an exact number of steps separates each pair of floors. If you know one count, arithmetic tells you the other. The same logic can work with lightwaves. Soon after the engineers developed mode-locking theory and a few tricks like frequency combs, they figured out ways to stabilize a maser by mode-locking it to a laser. It’s like gearing down a once-a-second pendulum to regulate the hour-hand of a clock, so of course they called it optical clockwork even though there’s no gears.”

“Maser?”

“A maser does microwaves the way a laser does lightwaves. Every tick from a cesium-based maser is about 47,000 ticks from a strontium-based laser. Mode-lock them together and your clock’s good within a few seconds over the age of the Universe.”

“Hiya, Eddie.”

“Hiya, Vinnie. Perfect timing. Those pizzas you called for, they’re just comin’ outta the oven.”

~~ Rich Olcott

Elevator, Locked And Loaded

On By rolcottIn Physics: Foundations of Measurement, Physics: Waves, UncategorizedLeave a comment

Vinnie’s on his phone again.  “Michael!  Where are you, man?  We’re still trapped in this elevator!  Ah, geez.”  <to me>  “Guy can’t find the special lever.”  <to phone>  “Well, use a regular prybar, f’petesake.”  <to me>  “Says he doesn’t want to damage the new door.”  <to phone>  “Find something else, then.  It’s way past dinner-time, I’m hungry, and Sy’s starting to look good, ya hear what I’m sayin’?  OK, OK, the sooner the better.”  <to me>  “Michael’s says he’s doin’ the best he can.”

“I certainly hope so.  Try chewing on one of your moccasins there.  It’d complain less than I would and probably taste better.”

“Don’t worry about it.  Yet.”  <looks at Old Reliable’s display, takes his notebook from a pocket, scribbles in it>  “That 1960 definition has more digits than the 1967 one.  Why’d they settle for less precision in the new definition?  Lemme guess — 1960s tech wasn’t up to counting frequencies any higher so they couldn’t get any better numbers?”

“Nailed it, Vinnie.  The International Bureau of Weights and Measures blessed the cesium-microwave definition just as laser technology began a whole cascade of advancements.  It started with mode-locking, which led to everything from laser cooling to optical clockwork.”

“We got nothing better to do until Michael. Go ahead, ‘splain those things.”

“Might as well, ’cause this’ll take a while. What do you know about how a laser works?”

“Just what I see in my magazines. You get some stuff that can absorb and emit light in the frequency range you like. You put that stuff in a tube with mirrors at each end but one of them’s leaky. You pump light in from the side. The stuff absorbs the light and sends it out again in all different directions. Light that got sent towards a mirror starts bouncing back and forth, getting stronger and stronger. Eventually the absorber gets saturated and squirts a whoosh of photons all in sync and they leave through the leaky mirror. That’s the laser beam. How’d I do?”

“Pretty good, you got most of the essentials except for the ‘saturated-squirting’ part. Not a good metaphor. Think about putting marbles on a balance board. As long as the board stays flat you can keep putting marbles on there. But if the board tilts, just a little bit, suddenly all the marbles fall off. It’s not a matter of how many marbles, it’s the balance. But what’s really important is that there’s lots of boards, one after the other, all down the length of the laser cavity, and they interact.”

“How’s that important?”

“Because then waves can happen. Marbles coming off of board 27 disturb boards 26 and 28. Their marbles unbalance boards 25 and 29 and so on. Waves of instability spread out and bounce off those mirrors you mentioned. New marbles coming in from the marble pump repopulate the boards so the process keeps going. Here’s the fun part — if a disturbance wave has just the right wavelength, it can bounce off of one mirror, travel down the line, bounce back off the other mirror, and just keep going. It’s called a standing wave.”

“I heard this story before, but it was about sound and musical instruments. Standing waves gotta exactly match the tube length or they die away.”

“Mm-hm, wave theory shows up all over Physics. Laser resonators are just another case.”

“You got a laser equivalent to overtones, like octaves and fourths?”

“Sure, except that laser designers call them modes. If one wave exactly fits between the mirrors, so does a wave with half the wavelength, or 1/3 or 1/4 and so on. Like an organ pipe, a laser can have multiple active modes. But it makes a difference where each mode is in its cycle. Here, let me show you on Old Reliable … Both graphs have time along the horizontal. Reading up from the bottom I’ve got four modes active and the purple line on top is what comes out of the resonator. If all modes peak at different times you just get a hash, but if you synchronize their peaks you get a series of big peaks. The modes are locked in. Like us in this elevator.”

“Michael! Get us outta here!”

~~ Rich Olcott

Three atop A Crosshatch

On By rolcottIn Chemistry, Physics: Fundamentals, Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

“Hey, Sy, what you said back there, ‘three and a fraction‘ ways to link atoms together…”

“Yeah, Vinnie?”

“What’s that about?  How do fractions come in when you’re counting?”

“Well, I was thinking about how atoms in separate molecules can interact short of reacting and forming new molecular orbitals.  I figure that as a fraction.”

“Charge sharing ain’t the whole story?”

“It would be except that sharing usually isn’t equal.  It depends on where the atoms are in the Periodic Table.”

“What’s it got to do with the Periodic Table?”

“The Table’s structure reflects atom structures — how many shells are active in a base-state atom of each element and how many units of charge are in its outermost shell.  Hydrogen and Helium are in Row 1 because the 1-node shell is the only active one in those atoms.  The atoms from Lithium to Neon in Row 2 have charge activating both the 1-node shell and the 2-node shell, and so on.”

“What’s that get us?”

“It gets us a feel for how the atoms behave.  You know I’m all about dimensions, right?”

“Ohhh, yeah.”

“OK, we’ve got a two-dimensional table here.  Going across, each atom’s nucleus has one more proton than its buddy to the left.  What’s that going to do to the electronic charge?”

“Gonna pull it in closer.”

“Wait, Vinnie, there’s an extra electron in there, too.  Won’t that cancel out the proton, Sy?”

“Good thinking, Eddie.  Yes, it does, but only partially.  The atoms do get smaller as you go across, but it’s irregular because negative-negative repulsion within a shell works to expand it almost as much as negative-positive attraction contracts it.”

“Bet things get bigger as you go down the Table, though.”

“Mostly, Vinnie, because each row down adds a shell that’s bigger than the shrinking inner shells.”

“Mostly?”

“The bigger shells with more nodes have more complex charge patterns than just balls and dumbbells.  Those two rows below the main table actually squinch into the lowest two boxes in the third column.  In those elements, some of the activated patterns barely shield the nucleus.  The atoms to their right in the main table are almost identical in size to the elements above them.”

“So I can guess an atom’s size.  So what?”

“So that and the charge give you a handle on the element’s properties and chemistry.  Up there in the top right corner you’ve got the atoms with the highest ratio of nuclear charge to size.  If given the opportunity to pull charge from atoms to their left and below them, what do you suppose happens?”

“You get lop-sided bonds, I guess.”

“Exactly.  In water, for instance, the Oxygen pulls charge towards itself and away from the Hydrogen atoms.  That makes each O-H bond a little dipole, positive-ish at the hydrogen end and negative-ish at the oxygen end.”

“Won’t the positive-ish ends pull on the negative-ish parts of next-door molecules?”

“You’ve just invented hydrogen bonding, Eddie.  That’s exactly what happens in liquid water.  Each molecule can link up like that with many adjacent ones and build a huge but floppy structure.  It’s floppy because hydrogen bonds are nowhere near as strong as orbital-sharing bonds.  Even so, the energy required to move through liquid H2O or to vaporize it is much greater than for liquid methane (CH4), ammonia (NH3) or any similar molecule.”

“Can that pull-away action go all the way?”

“You’ve just invented ionic bonding, Vinnie.  The elements in the Oxygen and Fluorine columns can extract charge completely away from many of those far to the left and below them.  Fluorine steals charge from Lithium, for instance.  Fluoride ions are net negative, lithium ions are net positive.  Opposites attract, same as always, but now it’s  entire ions that attract each other and you get crystals.”

“That’s your and-a-fraction?”

“Not quite, Vinnie.  There’s one more, Van der Waals forces.  They come from momentary polarizations as electron chaos sloshes back and forth in neighboring molecules.  They’re why solids are solid even without ionic or hydrogen bonding.”

“Geez, look at the time.  Rosalie’s got my dinner waiting.  Bye, guys, everybody out!”

~~ Rich Olcott

To Bond Or Not To Bond, That Is The Question

On By rolcottIn Chemistry, Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

Vinnie’s pushing pizza crumbs around his plate, watching them clump together.  “These molecular orbitals gotta be pretty complicated.  How do you even write them down?”

“Combinations.  There’s a bunch of different strategies, but they all go back to Laplace’s spherical harmonics.  Remember, he showed that every possible distribution around a central attractor could be described as a combination of his patterns.  Turn on a field, like from another atom, and you just change what combination is active.  Here’s a sketch of the simplest case, two hydrogen atoms — see how the charge on each one bulges toward the other?  The bulge is a combination of a spherical orbital and a dumbbell one.  The molecular orbitals are combinations of orbitals from both atoms, describing how the charges overlap, or not.”Hydrogen molecule

“What’s that blue in the other direction?”

“Another possible combination.  You can combine atomic orbitals with pluses or minuses.  The difference is that the minus combination will always have an additional node in between.  Extra nodes mean higher energy, harder to activate. When the molecule’s in the lowest energy state, charge will be between the atoms where that extra node isn’t.”

“So the overlapped charge here is negative, right, and it pulls the two positive nucleusses —”

“Nuclei”

“Whatever, it pulls ’em together.  Why don’t they just merge?”

“Positive-positive repulsion counts, too.  At the equilibrium bond distance, the nuclei repel each other exactly as much as the shared charge pulls them together.”

Eddie’s still hovering by our table.  “You said that there’s this huge number of possible atomic orbitals.  Wouldn’t there be an even huger number of molecular orbitals?”

“Sure.  The trick is in figuring out which of them are lowest-energy and activated and how that relates to the molecule’s configuration.  Keep track of your model’s total energy as you move the atoms about, for instance, and you can predict the equilibrium distance where the energy is a minimum.  In principle you can calculate configuration changes as two molecules approach each other and react.”

“Looks like a lot of work.”

“For sure, Eddie.  Even a handful of atoms has lots of atomic orbitals to keep track of.  That can burn up acres of compute time.”

Vinnie pushes three crumbs into a triangle.  “You got three distances, you can figure their angles.  So you got the whole shape of the thing.”

“Right, but like Eddie said, that’s a lot of computer work.  Chemists had to come up with shortcuts.  As a matter of fact, they had the shortcuts way before the computers came along.”

“They used, like, abacuses?”

“Funny, Vinnie.  No, no math at all.  And it’s why they still show school-kids those Bohr diagrams.”

“Crazy Eights.”

“Eddie, you got games on the brain.  But yeah, eights.  Or better, quartets of pairs.  One thing I’ve not mentioned yet is that even though they’ve got the same charge, electrons are willing to pair up.”

“How come?”

“That’s the thing of it, Vinnie.  There’s a story about Richard Feynman, probably the foremost physicist of the mid-20th Century.  Someone asked him to explain the pairing-up without using math.  Feynman went into his office for a week, came back out and said he couldn’t do it.  The math demands pairing-up, but outside of the math all we can say is experiments show that’s how it works.”

“HAH, that’s the reason for the ‘two charge units per orbital’ rule!”

“Exactly, Eddie.  It’s how charge can collect in that bonding molecular orbital in the first place.  It’s also the reason that helium doesn’t form molecules at all.  Imagine two helium atoms, each with two units of charge.  Suppose they come close to each other like those hydrogens did.  Where would the charge go?”

“OK, you got two units going into that in-between space, ahh, and the other two activating that blue orbital and pulling the two atoms apart.  So that adds up to zero?”

“Uh-huh.  They just bounce off and away.”

“Cool.”

“Hey, I got a question.  Your sketch has a ball orbital combining with a dumbbell.  But they’ve got different node counts, one and two.  Can you mix things from different shells?”

“Sure, Vinnie, if there’s enough energy.  The electron pair-up can release that much.”

“Cool.”

~~ Rich Olcott

  • A friend pointed out that I’m doing my best to avoid saying the word “electron.” He’s absolutely right.  At least in this series I’m taking Bohr’s side in his debate with Einstein — electrons in atoms don’t act like little billiard balls, they act like statistical averages, smeared-out ones at that.  It’s closer to reality to talk about where the charge is so that’s how I’m writing it.

The Shell You Say

On By rolcottIn Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

Everyone figures Eddie started his pizza place because he likes to eavesdrop.  No surprise, he wanders over to our table.  “I heard you guys talking about atoms and stuff and how Sy here don’t like Bohr’s model of electrons in atoms even though Bohr’s model and the shell model both account for hydrogen’s spectrum.  Why’s the shell model better?”

Vinnie comes back quick.  “Because it’s not physically impossible, for one thing.”

I’m on it.  “Because the shell model extends smoothly to atoms and ions in an electric or magnetic field.  Better yet, shell methods can be applied to molecules.”

“What do fields have to do with it?”

“It’ll help to know that some of those electron patterns come in sets.  The 2-node shell has three dumbbell shapes, for instance — one each along the x, y and z axes. Think about an atom all alone in space with no fields around.  How does it know which way z goes?””

“It don’t.  Everything’s gotta be in all directions, like spherical.”

Vinnie’s back in.  “I’m seeing an atom in an electric field, say up-to-down, it’s going to pull charge in one direction, say down.  So now the atom don’t look like no ball no more, right?”

orbital in a field
Vertical field on the right

“Right.  Once the atom’s got a special direction, those three dumbbells stop being equivalent.  We say that the field mixes together the spherical pattern (in atoms we’d call it an s-orbital) with that direction’s dumbbell (we’d call it a p-orbital) to make two combination orbitals.  One combination has a lump of charge stretched downwards and the other combination has a bowl of diminished charge stretched upwards.  The stronger the field, the wider the energy split between those two.”

“What about the other two dumbbells?”

“They’re still equivalent, Eddie.  If there’s charge in them it’s spread evenly around the equator like a doughnut.  Energy-wise they’re in between the two s±p combinations.”

“IF there’s charge, like maybe there ain’t?”

“Ever suspicious, eh, Vinnie?  You’re right, and that’s a good point.  Orbitals are only a way to describe the chaos inside the atom, like notes are a way to describe music.  There are 3-node orbitals and 47-node orbitals, all the way up, but most of the time they’re not charge-activated just like a piano’s top note hardly ever gets played.”

“How do we know whether an orbital’s activated?”

“We’ve got rules for that, Eddie.  Maximum of two units of charge per orbital, lowest energy first.  Unless some light wave has deactivated a deeper orbital and activated a higher one.”

“You’re being careful again, not saying an electron’s here or an electron’s there.”

“Darn right, Vinnie.  It’s that chaos thing — charge is smeared all over the atom like air molecules jiggle all over the place to carry a sound wave.  Chemists and physicists may talk about ‘the electron in the 2s-orbital’ but that’s shorthand.  They know it’s really not like that.”

“I’m doing arithmetic over here.  So there’s two electrons, OK, call it two units of charge for that 1-node ball orbital, plus two units for the 2-node ball, plus two units each for the three dumbbells, uses up five orbitals.  That’s the same 2+8 stable mix that Bohr came up with.”

“Yeah, Eddie, but that field Sy talked about could be any strength.  Run the energy  equations backwards and the astronomers get a way to check a star’s fields.”

“Exactly, Vinnie.  Transitions involving combination orbitals have slightly different energy jumps than the ones we see in isolated atoms.  Electric and magnetic fields split each line in an element’s spectrum into multiplets.  Measure their splittings and you can work back to the field strengths that caused them.  The shell theory offers more predictions and more scientific insights than Bohr’s model ever dreamed of.”

“You said shell theory can handle molecules, too.  How’s that work?”

“Same as that electric field, but a lot messier.  Every nucleus exerts a field, mostly electric, on the rest of the molecule.  So does all the electron charge, but it’s more diffuse and includes more magnetism.  Molecular orbitals span the whole thing.  Works like atoms but much harder to calculate.”

“Figuring tips is easier,” hints Eddie.

~~ Rich Olcott

The Music of The Spherical Harmonics

On By rolcottIn Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

Eddie’s diner serves tasty pizza, but his music playlist’s tasty, too — heavy with small-group vocals.  We’re talking atomic structure but suddenly Vinnie surprises me.  “Whoa, she’s got a hot voice!”

“Who?”

“That girl who’s singing.”

“Which one?  That’s a quartet.”

“The alto.”

“How can you pick one voice out of that close-harmony performance?”

“By listening!  She’s the only one singing those notes.”

“You’re hearing a chaotic sound wave yet you can pick out just one sound.”

“Yeah, just her special notes.”

“Interesting thing is, atoms do that, too.  Think about, say, a uranium atom, 92 electrons attracted by the nucleus, repelled by every other electron, all dashing about in the nuclear field and getting in each other’s way.  Think that’d be a nice, orderly picture?”

“Sure not.  It’d be, like you say, chaotic.”

“But just like we can describe a messy sound wave as a combination of frequencies, we can describe that atom’s electron structure as a combination of basic patterns.”  I pull Old Reliable from its holster and bring up an image.  “Here’s something I built for a presentation.  It’s a little busy so I’ll walk you through it.”Shell levels

“Busy, uh-huh.”

“Start with those blue circles.  They look familiar?”

“Right, they’re Laplace’s spherical patterns.  You got them sorted by how many blue spaces they got.”

“Yup.  Blue represents a node, a 2-D region where the value touches or crosses zero.  There are patterns with three or more nodes, but I ran out of space and patience to draw them.  Laplace showed there’s an infinite number of candidate patterns as you add more and more nodes.  You can describe any physically reasonable distribution around the central point as some combination of his patterns.”

“Why’d you draw them on stair-steps?”

“Because each step (we call it a shell) is at a different potential energy level.  Suppose, for instance, that there’s charge in that one-node pattern.  Moving it away from the nucleus puts a node there.  That’ll cost some energy and shift charge to the two-node shell.  To exclude it from there and also from another node, say a larger spherical surface, would take even more energy, and so on.”

“How is that potential energy?”

“We’re comparing shell energy to the energy of an electron that’s far away.  It’s like gravitational potential energy, maybe the energy a space rock converts to kinetic energy as it falls to Earth.  Call the far-away energy zero.  The numbers get more and more negative as the rock or the charge get closer to the center of attraction.”

“Ah, so that’s why you’ve got minus signs in the picture.”

“Exactly.  See zero at the top of the stairs?  With a hydrogen atom, for instance, an electron would give up 13.6 electron-volts of energy to get close to the nucleus in that 1-node pattern.  Conversely, it’d take 13.6 eV to rip that charge completely away.”

“If the 13.6 is what you’re calling ‘Minimum’, why not just write ‘–13.6’ in there?”

“It’s a different number for different atoms and even ions.  Astronomers see all kinds of ions with every amount of charge so they have to keep things general in their calculations.”

“What are those fractions about?  Wait, don’t tell me, I can figure this.  Each divisor is the square of its node count.  Are those the 1/n² numbers from whosit’s formula?”

“Rydberg’s.  You’re on the right track, keep going.”

“If the minimum is 13.6 eV, the diagram says that the two-node shell is … 3.4 eV down from the top and … 10.2 eV up from the bottom.  And from what we said about the hydrogen spectrum, I’ll bet that 10.2 eV jump is the first line in that, was it the Ly series, the one in the ultra-violet?”

“Bravo, Vinnie!  The Lyman series it is.  Excellent memory for detail there.”

“I noticed something else.  You carefully didn’t say we moved an electron between shells.”

“That’s an important point.  At the atomic size scale we can’t treat the electron as a particle moving around.  Lightwaves act to turn off one shell and excite another one, like your singer exciting a different note.”

“Yes, she does.”

~~ Rich Olcott

  • Thanks to the Molnars for a delightful meal, and to their dinner party guests the Jumps for instigating this post.

Shells A-poppin’

On By rolcottIn Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

We step into Eddie’s.  Vinnie spots Jeremy behind the gelato stand.  “Hey, kid, you studying something Science-y?”

“Yessir, my geology text.”

“Lemme see it a sec, OK?”

“Sure.  Want a gelato?”

“Yeah, gimme a pistachio, double-dip.  I’ll hold your book while you’re doing that.  Ah-hah, Sy, lookie here, page 37 — new textbook but this atom diagram coulda come right out of that 1912 Bohr paper you don’t like.  See, eight dots in a ring around the nucleus.  Can’t be wrong or it wouldn’t have survived this long, right?”

<sigh>  “What it is isn’t what it was.  Bohr proposed his model as a way to explain atomic spectra.  We’ve got a much better model now — but the two agree on three points.  Atoms organize their electronic charge in concentric shells, innermost shells deepest in the nuclear energy well.  Second, each shell has a limited capacity.  Third, when charge moves from one shell to another, light energy is absorbed or emitted to match the energy difference between shells.  Beyond those, not much.  Here, this diagram hints at the differences.”Better Bohr

“The scrambled-looking half is the new picture?”

“Pure chaos, where the only thing you can be sure of is the averages.  These days the Bohr model survives as just an accounting device to keep track of how much charge is in each shell.  That diagram — what kind of atom is it describing?”

“I dunno, two electrons inside, eight outside, ten total.”

“Could be neon, or a fluoride, oxide, sodium or magnesium ion.  From a quantum perspective they all look the same.”

“Here’s your gelato, sir.”

“Thanks, kid, here’s your book back.  But those are different elements, Sy.”

“The important thing, Vinnie, is they all have an outer shell with eight units of charge.  That’s the most stable configuration.”

“What’s so special about eight, Mr Moire?  If it’s pure chaos shouldn’t any number be OK?”

“Like I said, Jeremy, it’s the averages that count.  Actually, this is one of my favorite examples of what Wigner called ‘The Unreasonable Effectiveness of Mathematics in the Natural Sciences.’  Back in 1782, a century and a quarter before anyone took atoms seriously, Laplace did some interesting math.  Have you ever waited for a pot of water to boil and spent the time tapping the pot to see the ripples?”

“Who hasn’t?  Doesn’t boil any faster, though.”

“True.  Looking at those waves, you saw patterns you don’t see with flat reflectors, right?”

“Oh, yeah — some like dumbbells, a lot of circles.”

“Mm-hm.  In a completely random situation all possible patterns could appear, but the pot’s circular boundary suppresses everything except wave patterns that match its symmetry.  You don’t see hexagons, for instance.”

“That’s right, I didn’t.”

“So there’s Laplace in the 1790s, thinking about Newton’s Law of Gravity, and he realizes that even in the boundaryless Solar System there’s still a boundary condition — any well-behaved standing wave has to have the same value at the central point no matter what direction you come from.  He worked out all the possible stable patterns that could exist in a central field like that.  Some of them look like what you saw in the water.  We now classify them by symmetry and node count.”

“Node?”Disk orbitals

“A region where the pattern hits zero, Vinnie.  Density waves range from zero to some positive value; other kinds range from positive to negative values.  A spherical wave could peak at the center and then go to zero infinitely far away.  One node.  Or it could be zero at the center, peak in a spherical shell some distance out and then fade away.  That’d be two nodes.  Or it could be zero at the center, zero far away, and have two peaks at different distances with a spherical third node in between.  Here’s another two-node pattern — that dumbbell shape with nodes at the center and infinity.  You can add radial nodes partway out.”

“I’m getting the picture.”

“Sure.  You might think Laplace’s patterns are just pretty pictures, but electron charge in atoms and ions just happens to collect in exactly those patterns.  Combine Laplace’s one-node and two-node patterns, you get the two lowest-energy stable shells.  They hold exactly ten charge units.  The energies are right, too.  Effective?”

“Unreasonably.”

~~ Rich Olcott

Gravity’s Real Rainbow

On By rolcottIn Astronomy: Multi-messenger, Astronomy: Stellar Science, Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Waves, UncategorizedLeave a comment

Some people are born to scones, some have scones thrust upon them.  As I stepped into his coffee shop this morning, Al was loading a fresh batch onto the rack.  “Hey, Sy, try one of these.”

“Uhh … not really my taste.  You got any cinnamon ones ready?”

“Not much for cheddar-habañero, huh?  I’m doing them for the hipster trade,” waving towards all the fedoras on the room.  “Here ya go.  Oh, Vinnie’s waiting for you.”

I navigated to the table bearing a pile of crumpled yellow paper, pulled up a chair.  “Morning, Vinnie, how’s the yellow writing tablet working out for you?”

“Better’n the paper napkins, but it’s nearly used up.”

“What problem are you working on now?”

“OK, I’m still on LIGO and still on that energy question I posed way back — how do I figure the energy of a photon when a gravitational wave hits it in a LIGO?  You had me flying that space shuttle to explain frames and such, but kept putting off photons.”

“Can’t argue with that, Vinnie, but there’s a reason.  Photons are different from atoms and such because they’ve got zero mass.  Not just nearly massless like neutrinos, but exactly zero.  So — do you remember Newton’s formula for momentum?”

“Yeah, momentum is mass times the velocity.”

“Right, so what’s the momentum of a photon?”

“Uhh, zero times speed-of-light.  But that’s still zero.”

“Yup.  But there’s lots of experimental data to show that photons do carry non-zero momentum.  Among other things, light shining on an an electrode in a vacuum tube knocks electrons out of it and lets an electric current flow through the tube.  Compton got his Nobel prize for that 1923 demonstration of the photoelectric effect, and Einstein got his for explaining it.”

“So then where’s the momentum come from and how do you figure it?”

“Where it comes from is a long heavy-math story, but calculating it is simple.  Remember those Greek letters for calculating waves?”

(starts a fresh sheet of note paper) “Uhh… this (writes λ) is lambda is wavelength and this (writes ν) is nu is cycles per second.”

“Vinnie, you never cease to impress.  OK, a photon’s momentum is proportional to its frequency.  Here’s the formula: p=h·ν/c.  If we plug in the E=h·ν equation we played with last week we get another equation for momentum, this one with no Greek in it:  p=E/c.  Would you suppose that E represents total energy, kinetic energy or potential energy?”

“Momentum’s all about movement, right, so I vote for kinetic energy.”

“Bingo.  How about gravity?”

“That’s potential energy ’cause it depends on where you’re comparing it to.”

light-in-a-gravity-well“OK, back when we started this whole conversation you began by telling me how you trade off gravitational potential energy for increased kinetic energy when you dive your airplane.  Walk us through how that’d work for a photon, OK?  Start with the photon’s inertial frame.”

“That’s easy.  The photon’s feeling no forces, not even gravitational, ’cause it’s just following the curves in space, right, so there’s no change in momentum so its kinetic energy is constant.  Your equation there says that it won’t see a change in frequency.  Wavelength, either, from the λ=c/ν equation ’cause in its frame there’s no space compression so the speed of light’s always the same.”

“Bravo!  Now, for our Earth-bound inertial frame…?”

“Lessee… OK, we see the photon dropping into a gravity well so it’s got to be losing gravitational potential energy.  That means its kinetic energy has to increase ’cause it’s not giving up energy to anything else.  Only way it can do that is to increase its momentum.  Your equation there says that means its frequency will increase.  Umm, or the local speed of light gets squinched which means the wavelength gets shorter.  Or both.  Anyway, that means we see the light get bluer?”

“Vinnie, we’ll make a physicist of you yet.  You’re absolutely right — looking from the outside at that beam of photons encountering a more intense gravity field we’d see a gravitational blue-shift.  When they leave the field, it’s a red-shift.”

“Keeping track of frames does make a difference.”

Al yelled over, “Like using tablet paper instead of paper napkins.”

~~ Rich Olcott

The Solar System is in gear

On By rolcottIn Astronomy: Planetary Science, Astronomy: Stellar Science, Physics: Waves, UncategorizedLeave a comment

Pythagoras was onto far more than he knew.  He discovered that a stretched string made a musical tone, but only when it was plucked at certain points.  The special points are those where the string lengths above and below the point are in the ratio of small whole numbers — 1:1, 1:2, 2:3, ….  Away from those points you just get a brief buzz.  All of Western musical theory grew out of that discovery.

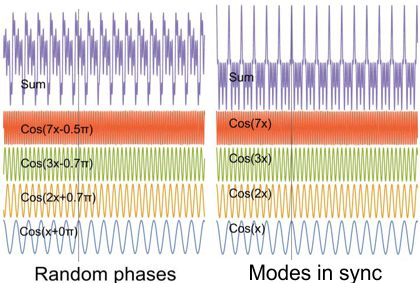
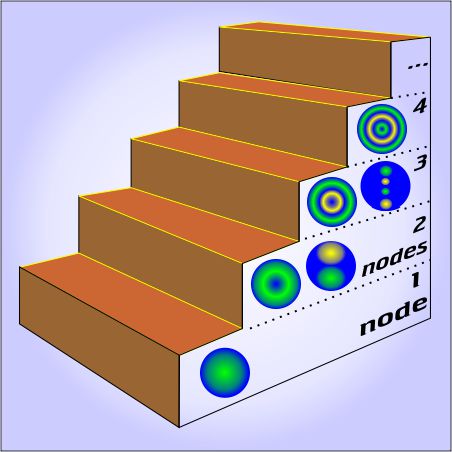
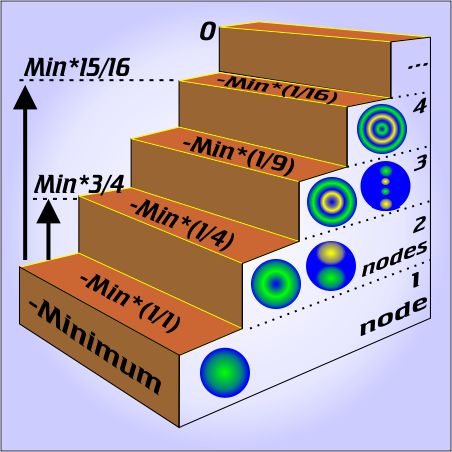
sinesThe underlying physics is straightforward.  The string produces a stable tone only if its motion has nodes at both ends, which means the vibration has to have a whole number of nodes, which means you have to pluck halfway between two of the nodes you want.  If you pluck it someplace like 39¼:264.77 then you excite a whole lot of frequencies that fight each other and die out quickly.

That notion underlies auditorium acoustics and aircraft design and quantum mechanics.  In a way, it also determines where objects reside in the Solar System.

If you’ve got a Sun with only one planet, that planet can pick any orbit it wants — circular or grossly elliptical, close approach or far, constrained only by the planet’s kinetic energy.

If you toss in a second planet it probably won’t last long — the two will smash together or one will fall into the Sun or leave the system.  There are half-a-dozen Lagrange points, special configurations like “all in a straight line” where things are stable.  Other than those, a three-body system lives in chaos — not even a really good computer program can predict where things will be after a few orbits.

geared-saturnAdd a few more planets in a random configuration and stability goes out the window — but then something interesting happens.  It’s 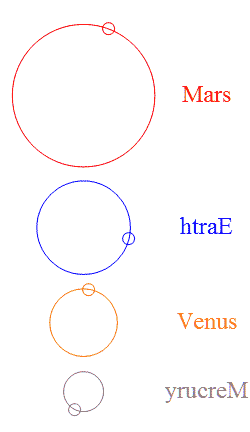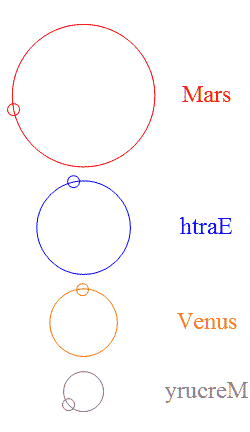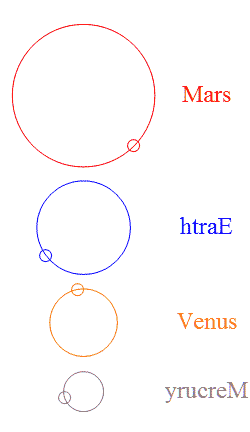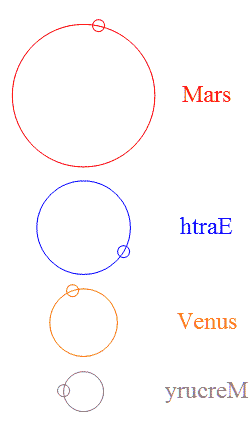the Chladni effect all over again.  Planets and dust and everything go rampaging around the system.  After a while (OK, a billion years or so) sweet-spot orbits start to appear, special niches where a planet can collect small stuff but where nothing big comes close enough to break it apart.  It’s not like each planet seeks shelter, but if it finds one it survives.

It’s a matter of simple arithmetic and synchrony.  Suppose you’re in a 600-day orbit.  Neighbor Fred looking for a good spot to occupy could choose your same 600-day orbit but on the other side of the Sun from you.  But that’s a hard synchrony to maintain — be off by a few percent and in just a few years, SMASH!

The next safest place would be in a different orbit but still somehow in synchrony with yours.  Inside your orbit Fred has to go faster and therefore has a shorter orbital period than yours.  Suppose Fred’s year is exactly 300 days (a 2:1 period ratio, like a 2:1 gear ratio).  Every six months he’s sort-of close to you but the rest of the time he’s far away.

Our Solar System does seem to have developed using gear-year logic.  Adjacent orbital years are very close to being in whole-number ratios.  Mercury, for instance, circles the Sun in about 88 days.  That’s just 2% away from 2/5 of Venus’s 225¾ days.

This table shows year-lengths for the Sun’s most prominent hangers-on, along with ratios for adjacent objects.  For the “ideal” ratios I arbitrarily picked nearby whole-number multiples of 2.  I calculated how long each object’s year “should” be compared to its lower neighbor — the average inaccuracy across all ten objects is only 0.18%.

Object
Period, years
2 × shorter / longer period
“Ideal” ratio
“Ideal” period, years
Real/”Ideal”
Mercury
0.24
0.24
Venus
0.62
5.11
5 : 2
0.60
102%
Earth
1.00
3.25
3 : 2
0.92
108%
Mars
1.88
3.76
4 : 2
2.00
94%
Ceres
4.60
4.89
5 : 2
4.70
98%
Jupiter
11.86
5.16
5 : 2
11.50
103%
Saturn
29.46
4.97
5 : 2
29.65
99%
Uranus
84.02
5.70
6 : 2
88.37
95%
Neptune
164.80
3.92
4 : 2
168.04
98%
Pluto
248.00
3.01
3 : 2
247.20
100%

gears-2The usual rings-around-the-Sun diagram doesn’t show the specialness of the orbits we’ve got.  This chart shows the four innermost planets in their “ideal” orbits, properly scaled and with approximately the right phases.  I used artistic license to emphasize the gear-like action by reversing Earth’s and Mercury’s direction.   Earth and Mars are never near each other, nor are Earth and Venus.

It doesn’t show up in this video’s time resolution, but Venus and Mercury demonstrate another way the gears can work.  Mercury nears Venus twice in each full 5-year cycle, once leading and once trailing.  The leading pass slows Mercury down (raising it towards Venus), but the trailing pass speeds it up again.  Net result — safe!

~~ Rich Olcott