The Ideal Gas Game

On August 12, 2024November 27, 2025 By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Fundamentals, UncategorizedLeave a comment

“But Uncle Sy, you never did answer my real question!”

“What question was that, Teena?”

“About the helium planet. With oxygen. Oh, I guess I never did get around to asking that part of it. You side‑tracked us into how a helium‑oxygen atmosphere would be unstable unless it was really cold or the planet had more gravity than Earth so the helium wouldn’t fly away. But what I wanted to know was, what would it be like before the helium left? Like, could we fly a plane there?”

“Mmm, let’s get a leetle more specific. You asked about swapping all of Earth’s atmospheric nitrogen with helium. Was that one helium atom for each nitrogen molecule or each nitrogen atom?”

“What difference would that make?”

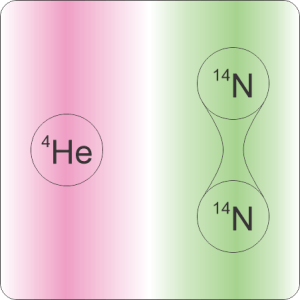
“Mass, to begin with. A helium atom weighs about ¹/₃ of a nitrogen atom, ¹/₇ of a nitrogen molecule. The atmospheric pressure we feel is the weight of all the air molecules above us. Swap out 80% of those molecules for something lighter, pressure goes down whether we swap helium for molecules or helium for atoms. We could calculate either one. But the change would be much harder to calculate for the atom‑for‑atom swap.”

“Why?”

“Mmm, have you gotten into equations yet in school?”

“You mean algebra, like 3x+7=8x+2? Yeah, they’re super‑easy.”

“This won’t even be as complicated as that. Here’s a famous Physics equation called The Ideal Gas Law — PV=nRT. Each letter stands for one quantity. Two adjacent quantities are multiplied together, okay? The pressure in a container is P, the container’s volume is V, T is the absolute temperature, and n is a measure of how much gas is in there.”

“You skipped R.”

“Yes, I did. It’s a constant number. Its job is to make all the units come out right. For instance, if the pressure’s in atmospheres, the volume’s in liters, n is in grams of helium and the temperature is in kelvins, then R is 0.021. Suppose you’re holding a balloon filled with helium and it’s at room temperature. What can you say about the gas?”

“Umm, all the nRT stuff doesn’t change so P times V, whatever it is, doesn’t change either.”

“If we let it fly upward until the pressure was only half what it is here…?”

“Then V would double. The balloon would get twice as big. Unless it burst, right?”

“You got the idea. Okay, now let’s fiddle with the right-hand side. Suppose we double the amount of helium.”

“P times V must get bigger but we don’t know which one.”

“Why not both?”

“Wooo… Each one could get some bigger… Oh, wait, I’m holding the balloon so the pressure’s not going to change so the balloon gets twice bigger.”

“Good thinking. One more thing and we can get back to your difference question. The Ideal Gas Law doesn’t care what kind of gas you’re working with. All the n quantity really cares about is how many particles are in the gas. A particle can be anything that moves about independently of anything else — helium atom or nitrogen molecule, doesn’t matter. If you change the definition of what n is measuring, all that happens is you have to adjust R so the units come out right. Then the equation works fine. Next step—”

“Wait, Uncle Sy, I want to think this atom‑or‑molecule thing through for myself. I’m gonna ignore R times T because both of them stay the same. So if we swap one atom of helium for one molecule of nitrogen, the number of particles doesn’t change and PV doesn’t change. But if we swap one atom of helium for each atom of nitrogen then n doubles and so does PV. But if we do that for the whole atmosphere then we can’t say that the pressure won’t change because the atmosphere could just expand and that’s the V but the pressures are all different as you go higher up anyway. Oh, wait, T changes, too, because it’s cold up there. It’s complicated, isn’t it?”

“It certainly is. Can we stick to just the simple atom‑for‑molecule swap?”

“Uh‑huh.”

~~ Rich Olcott

Thanks again, Xander, and happy birthday. Your question was deeper than I thought.

Fields of Dreams

On March 18, 2024November 30, 2025 By rolcottIn Cosmology, Physics: Quantum Mechanics, Physics: Waves, Uncategorized1 Comment

Vinnie takes a slug of his coffee. “So the gravitational field carries the gravitational wave. I suppose Einstein would blame sound waves on some kind of field?”

I take a slug of mine. “Mm-hm. We techies call it a pressure field. Can’t do solar physics without it. The weather maps you use when plotting up a flight plan — they lay three fields on top of the geography.”

“Lessee — temp, wind … and barometer reading. In the old days I’d use that one to calibrate my altimeter. You say those are fields?”

“In general, if a variable has a value at every point in the region of interest, the complete set of values is a field. Temperature and pressure are the simplest type. Their values are just numbers. Each point in a wind field has both speed and direction, two numbers treated as a single value, so you’ve got a field of vector values.”

“Oh, I know vectors, Sy. I’m a pilot, remember? So you’re saying instead of looking at molecules back‑and‑forthing to make sound waves we step back and look at just the pressure no matter the molecules. Makes things simpler, I can see that. Okay, how about the idea those other guys had?”

“Hm? Oh, the other wave carrier idea. Einstein’s gravitational waves are just fine, but the Quantum Field Theorists added a collection of other fields, one for each of the 17 boxes in the Standard Model.”

“Boxes?”

<displaying Old Reliable’s screen> “Here’s the usual graphic. It’s like the chemist’s Periodic Table but goes way below the atomic level. There’s a box each for six kinds of quarks; another half‑dozen for electrons, neutrinos and their kin; four more boxes for mediating electromagnetism and the weak and strong nuclear forces. Finally and at last there’s a box for the famous Higgs boson which isn’t about gravity despite what the pop‑sci press says.”

“What’s in the boxes?”

“Each box holds a list of properties — rest mass, spin, different kinds of charge, and a batch of rules for how to interact with the other thingies.”

“Thingies, Sy? I wouldn’t expect that word from you.”

“I would have said ‘particle‘ but that would violate QFT’s tenets despite the graphic’s headline.”

“Tenets? That word sounds more like you. What’s the problem?”

“That the word ‘particle‘ as we normally use it doesn’t really apply at the quantum field level. Each box names a distinct field that spreads its values and waves all across the Universe. There’s an electron field, a photon field, an up‑quark field, a down‑quark field, and so on. According to QFT, what we’d call a particle is nothing more than a localized peak in its underlying field. Where you find a peak you’ll find all the properties listed in its box. Wherever the field’s value is below its threshold, you find none of them.”

“All or none, huh? I guess that’s where quantum comes in. Wait, that means there could be gazillions of one of them popping up wherever, like maybe a big lump of one kind all right next to each other.”

“No, the rules prevent that. Quarks, for instance, only travel in twos or threes of assorted kinds. The whole job of the gluons is to enforce QFT rules so that, for instance, two up‑quarks and a down‑quark make a proton but only if they have different color charges.”

“Wait, color charge?”

“Not real colors, just quantum values that could as easily have been labeled 1, 2, 3 or A, B, C. There’s also an anti- for each value so the physicists could have used ±1, ±2, ±3, but they didn’t, they used ‘red’ and ‘anti‑red’ and so forth. And ‘color charge‘ is a different property from electric charge. Gluons only interact with color charge, photons only interact with electric charge. The rules are complicated.”

“You said ‘waves.’ Each of these fields can have waves like gravity waves?”

“Absolutely. We can’t draw good pictures of them because they’re 3‑dimensional. And they’re constantly in motion, of course.”

“How fast can those waves travel?”

“The particles are limited to lightspeed or slower; the waves, who knows?”

“Ripples zipping around underneath the quantum threshold could account for entanglement, ya’ know?”

“Maybe.”

~~ Rich Olcott

The Thin Edge of Infinity

On May 22, 2017November 30, 2025 By rolcottIn Physics: Black Holes and Relativity, UncategorizedLeave a comment

Late in the day, project’s half done but it’s hungry time. I could head home for a meal and drive back, but instead I board the elevator down to Eddie’s Pizza on the second floor. The door opens on 8 and Jeremy gets on, with a girl.

“Oh, hi, Mr. Moire. Didja see I hit a triple in the last game? What if the Sun became a black hole? This is that English girl I told you about.”

“Hello, Jennie.”

“Wotcha, Sy.”

“You know each other?”

“Ra-ther. He wrote me into his blog a year ago. You were going on about particles then, right, Sy?”

“Right, Jennie, but that was particles confined in atoms. Jeremy’s interested in larger prey.”

“So I hear.”

The elevator lets us out at Eddie’s place. We luck into a table, order and resume talking. I open with, “What’s a particle?”

“Well, Sy, your post with Jeremy says it’s an abstract point with a minimal set of properties, like mass and charge, in a mathematical model of a real object with just that set of properties.”

“Ah, you’ve been reading my stuff. That simplifies things. So when can we treat a black hole like a particle? Did you see anything about that in my archives, Jennie?”

“The nearest I can recall was Professor ‘t Hooft’s statement. Ermm… if the Sun’s so far away that we can calculate planetary orbits accurately by treating it as a point, then we’re justified in doing so.”

“And if the Sun were to suddenly collapse to a black hole?”

“It’d be a lot smaller, even more like a point. No change in gravity then. But wouldn’t Earth be caught up in relativity effects like space compression?’

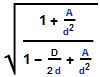
“Not unless you’re really close. Space compression around a non-rotating (Schwarzchild) black hole scales by a factor that looks like , where D is the object’s diameter and d is your distance from it. Suppose the Sun suddenly collapsed without losing any mass to become a Schwarzchild object. The object’s diameter would be a bit less than 4 miles. Earth is 93 million miles from the Sun so the compression factor here would be [poking numbers into my smartphone] 1.000_000_04. Nothing you’d notice. It’d be 1.000_000_10 at Mercury. You wouldn’t see even 1% compression until you got as close as 378 miles, 10% only inside of 43 miles. Fifty percent of the effect shows up in the last 13 miles. The edge of a black hole is sharper than this pizza knife.”

“How about if it’s spinning? Ms Plenum referred me to a reading about frame-dragging.”

“Ah, Jeremy, you’re thinking of Gargantua, the Interstellar movie’s strangely lopsided black hole. I just ran across this report by Robbie Gonzalez. He goes into detail on why the image is that way, and why it should have looked more like this picture. Check out the blueshift on the left and the shift into the infra-red on the right.”

better Gargantua — A more accurate depiction of Gargantua. Image from
James, et al., **Class. Quantum Grav. 32** (2015) 065001 (41pp),
licensed under **CC BY-NC-ND 3.0**

[both] “Awesome!”

“So it’s the spin making the weirdness then, Sy?”

“Yes, ma’am. If Gargantua weren’t rotating, then the space around it would be perfectly spherical. As Gonzalez explains, the movie’s plotline needed an even more extreme spacetime distortion than they could get from that. Dr Kip Thorne, their physics guru, added more by spinning his mathematical model nearly up to the physical limit.”

“I’ll bite, Mr Moire. What’s the limit?”

“Rotating so fast that points on the equator would be going at lightspeed. Can’t do that. Anyhow, extreme spin alters spacetime distortion, which goes from spherical to pumpkin-shaped with a twist. The radial scaling changes form, too, from to . A is proportional to spin. When A is small (not much spin) or the distance is large those A/d² terms essentially vanish relative to the others and the scaling looks just like the simple almost-a-point Schwarzchild case. When A is large or the distance is small the A/d² terms dominate top and bottom, the factor equals 1 and there’s dragging but no compression. In the middle, things get interesting and that’s where Dr Thorne played.”

“So no relativity jolt to Earth.”

“Yep.”

“Here’s your pizzas.”

“Thanks, Eddie.”

[sounds of disappearing pizza]

~~ Rich Olcott

No-hair today, grown tomorrow

On May 15, 2017November 29, 2025 By rolcottIn Physics: Black Holes and Relativity, Physics: Quantum Mechanics, UncategorizedLeave a comment

It was a classic May day, perfect for some time by the lake in the park. I was watching the geese when a squadron of runners stampeded by. One of them broke stride, dashed my way and plopped down on the bench beside me. “Hi, Mr Moire. <pant, pant>”

“Afternoon, Jeremy. How are things?”

“Moving along, sir. I’ve signed up for track, I think it’ll help my base-running, I’ve met a new girl, she’s British, and that virtual particle stuff is cool but I’m having trouble fitting it into my black hole paper.”

“Here’s one angle. Nobelist Gerard ‘t Hooft said, ‘A particle is fundamental when it’s useful to think of it as fundamental.‘ In that sense, a black hole is a fundamental particle. Even more elementary than atoms, come to think of it.”

“Huh?”

“It has to do with the how few numbers you need to completely specify the particle. You’d need a gazillion terabytes for just the temperatures in the interior and oceans and atmosphere of Earth. But if you’re making a complete description of an isolated atom you just need about two dozen numbers — three for position, three for linear momentum, one for atomic number (to identify which element it represents), one for its atomic weight (which isotope), one for its net charge if it’s been ionized, four more for nuclear and electronic spin states, maybe three or four each for the energy levels of its nuclear and electronic configuration. So an atom is simpler than the Earth”

“And for a black hole?”

“Even simpler. A black hole’s event horizon is smooth, so smooth that you can’t distinguish one point from another. Therefore, no geography numbers. Furthermore, the physics we know about says whatever’s inside that horizon is completely sealed off from the rest of the universe. We can’t have knowledge of the contents, so we can’t use any numbers to describe it. It’s been proven (well, almost proven) that a black hole can be completely specified with only eleven numbers — one for its total mass-energy, one for its electric charge, and three each for position, linear momentum and angular momentum. Leave out the location and orientation information and you’ve got three numbers — mass, charge, and spin. That’s it.”

“How about its size or it temperature?”

“Depends how you measure size. Event horizons are spherical or nearly so, but the equations say the distance from an event horizon to where you’d think its center should be is literally infinite. You can’t quantify a horizon’s radius, but its diameter and surface area are both well-defined. You can calculate both of them from the mass. That goes for the temperature, too.”

“How about if it came from antimatter instead of matter?”

“Makes no difference because the gravitational stresses just tear atoms apart.”

“Wait, you said, ‘almost proven.’ What’s that about?”

“Believe it or not, the proof is called The No-hair Theorem. The ‘almost’ has to do with the proof’s starting assumptions. In the simplest case, zero change and zero spin and nothing else in the Universe, you’ve got a Schwarzchild object. The theorem’s been rigorously proven for that case — the event horizon must be perfectly spherical with no irregularities — ‘no hair’ as one balding physicist put it.”

“How about if the object spins and gets charged up, or how about if a planet or star or something falls into it?”

“Adding non-zero spin and charge makes it a Kerr-Newman object. The theorem’s been rigorously proven for those, too. Even an individual infalling mass has only a temporary effect. The black hole might experience transient wrinkling but we’re guaranteed that the energy will either be radiated away as a gravitational pulse or else simply absorbed to make the object a little bigger. Either way the event horizon goes smooth and hairless.”

“So where’s the ‘almost’ come in?”

“Reality. The region near a real black hole is cluttered with other stuff. You’ve seen artwork showing an accretion disk looking like Saturn’s rings around a black hole. The material in the disk distorts what would otherwise be a spherical gravitational field. That gnarly field’s too hairy for rigorous proofs, so far. And then Hawking pointed out the particle fuzz…”

~~ Rich Olcott

Abstract Horses

On April 24, 2017November 28, 2025 By rolcottIn Physics: Einstein, Physics: Newton and Gravity, Physics: Quantum Mechanics, UncategorizedLeave a comment

It was a young man’s knock, eager and a bit less hesitant than his first visit.

“C’mon in, Jeremy, the door’s open.”

“Hi, Mr Moire, it’s me, Jerem… How did ..? Never mind. Ready for my black hole questions?”

“I’ll do what I can, Jeremy, but mind you, even the cosmologists are still having a hard time understanding them. What’s your first question?”

“I read where nothing can escape a black hole, not even light, but Hawking radiation does come out because of virtual particles and what’s that about?”

“That’s a very lumpy question. Let’s unwrap it one layer at a time. What’s a particle?”

“A little teeny bit of something that floats in the air and you don’t want to breathe it because it can give you cancer or something.”

“That, too, but we’re talking physics here. The physics notion of a particle came from Newton. He invented it on the way to his Law of Gravity and calculating the Moon’s orbit around the Earth. He realized that he didn’t need to know what the Moon is made of or what color it is. Same thing for the Earth — he didn’t need to account for the Earth’s temperature or the length of its day. He didn’t even need to worry about whether either body was spherical. His results showed he could make valid predictions by pretending that the Earth and the Moon were simply massive points floating in space.”

“Accio abstractify! So that’s what a physics particle is?”

“Yup, just something that has mass and location and maybe a velocity. That’s all you need to know to do motion calculations, unless the distance between the objects is comparable to their sizes, or they’ve got an electrical charge, or they move near lightspeed, or they’re so small that quantum effects come into play. All other properties are irrelevant.”

“So that’s why he said that the Moon was attracted to Earth like the apple that fell on his head was — in his mind they were both just particles.”

“You got it, except that apple probably didn’t exist.”

“Whatever. But what about virtual particles? Do they have anything to do with VR goggles and like that?”

“Very little. The Laws of Physics are optional inside a computer-controlled ‘reality.’ Virtual people can fly, flow of virtual time is arbitrary, virtual electrical forces can be made weaker or stronger than virtual gravity, whatever the programmers decide will further the narrative. But virtual particles are much stranger than that.”

“Aw, they can’t be stranger than Minecraft. Have you seen those zombie and skeleton horses?”

“Yeah, actually, I have. My niece plays Minecraft. But at least those horses hang around. Virtual particles are now you might see them, now you probably don’t. They’re part of why quantum mechanics gave Einstein the willies.”

“Quantum mechanics comes into it? Cool! But what was Einstein’s problem? Didn’t he invent quantum theory in the first place?”

“Oh, he was definitely one of the early leaders, along with Bohr, Heisenberg, Schrödinger and that lot. But he was uncomfortable with how the community interpreted Schrödinger’s wave equation. His row with Bohr was particularly intense, and there’s reason to believe that Bohr never properly understood the point that Einstein was trying to make.”

“Sounds like me and my Dad. So what was Einstein’s point?”

“Basically, it’s that the quantum equations are about particles in Newton’s sense. They lead to extremely accurate predictions of experimental results, but there’s a lot of abstraction on the way to those concrete results. In the same way that Newton reduced Earth and Moon to mathematical objects, physicists reduced electrons and atomic nuclei to mathematical objects.”

“So they leave out stuff like what the Earth and Moon are made of. Kinda.”

“Exactly. Bohr’s interpretation was that quantum equations are statistical, that they give averages and relative probabilities –”

“– Like Schrödinger’s cat being alive AND dead –”

“– right, and Einstein’s question was, ‘Averages of what?‘ He felt that quantum theory’s statistical waves summarize underlying goings-on like ocean waves summarize what water molecules do. Maybe quantum theory’s underlying layer is more particles.”

“Are those the virtual particles?”

“We’re almost there, but I’ve got an appointment. Bye.”

“Sure. Uhh… bye.”

~~ Rich Olcott

Think globally, act locally. Electrons do.

On May 16, 2016November 30, 2025 By rolcottIn Physics: Quantum Mechanics, UncategorizedLeave a comment

“Watcha, Johnnie, you sure ‘at particle’s inna box?”
“O’course ’tis, Jennie! Why wouldn’t it be?”
“Me Mam sez particles can tunnel outta boxes ’cause they’re waves.”
“Can’t be both, Jessie.”

Maybe it can.

Nobel-winning (1965) physicist Richard Feynman said the double-slit experiment (diagrammed here) embodies the “central mystery” of Quantum Mechanics.

When the bottom slit is covered the display screen shows just what you’d expect — a bright area opposite the top slit.

When both slits are open, the screen shows a banded pattern you see with waves. Where a peak in a top-slit wave meets a peak in the bottom-slit wave, the screen shines brightly. Where a peak meets a trough the two waves cancel and the screen is dark. Overall there’s a series of stripes. So electrons are waves, right?

But wait. If we throttle the beam current way down, the display shows individual speckles where each electron hits. So the electrons are particles, right?

Now for the spooky part. If both slits are open to a throttled beam those singleton speckles don’t cluster behind the slits as you’d expect particles to do. A speckle may appear anywhere on the screen, even in an apparently blocked-off region. What’s more, when you send out many electrons one-by-one their individual hits cluster exactly where the bright stripes were when the beam was running full-on.

It’s as though each electron becomes a wave that goes through both slits, interferes with itself, and then goes back to being a particle!

By the way, this experiment isn’t a freak observation. It’s been repeated with the same results many times, not just with electrons but also with light (photons), atoms, and even massive molecules like buckyballs (fullerene spheres that contain 60 carbon atoms). In each case, the results indicate that the whatevers have a dual character — as a localized particle AND as a wave that reacts to the global environment.

Physicists have been arguing the “Which is it?” question ever since Louis-Victor-Pierre-Raymond, the 7th Duc de Broglie, raised it in his 1924 PhD Thesis (for which he received a Nobel Prize in 1929 — not bad for a beginner). He showed that any moving “particle” comes along with a “wave” whose peak-to-peak wavelength is inversely proportional to the particle’s mass times its velocity. The longer the wavelength, the less well you know where the thing is.

I just had to put numbers to de Broglie’s equation. With Newton in mind, I measured one of the apples in my kitchen. To scale everything, I assumed each object moved by one of its diameters per second. (OK, I cheated for the electron — modern physics says it’s just a point, so I used a not-really-valid classical calculation to get something to work with.)

“Particle”	Mass, kilograms	Diameter, meters	Wavelength, meters	Wavelength, diameters
Apple	0.2	0.07	7.1×10^-33	1.0×10^-31
Buckyball	1.2×10^-24	1.0×10^-9	0.083	8.3×10⁺⁷
Hydrogen atom	1.7×10^-27	1.0×10^-10	600	6.0×10⁺¹²
Electron	9.1×10^-31	3.0×10^-17	3.7×10⁺¹²	1.2×10⁺²⁹

That apple has a wave far smaller than any of its hydrogen atoms so I’ll have no trouble grabbing it for a bite. Anything tinier than a small virus is spread way out unless it’s moving pretty fast, as in a beam apparatus. For instance, an electron going at 1% of light-speed has a wavelength only a nanometer wide.

Different physicists have taken different positions on the “particle or wave?” question. Duc de Broglie claimed that both exist — particles are real and they travel where their waves tell them to. Bohr and Heisenberg went the opposite route, saying that the wave’s not real, it’s only a mathematical device for calculating relative probabilities for measuring this or that value. Furthermore, the particle doesn’t exist as such until a measurement determines its location or momentum. Einstein and Schrödinger liked particles. Feynman and Dirac just threw up their hands and calculated.

Which brings us to the other kind of quantum spookiness — “entanglement.” In fact, Einstein actually used the word spukhafte (German for “spooky”) in a discussion of the notion. He really didn’t like it and for good reason — entanglement rudely collides with his own Theory of Relativity. But that’s another story.

~~ Rich Olcott

Location, Location, Location

On May 9, 2016November 28, 2025 By rolcottIn Physics: Quantum Mechanics, UncategorizedLeave a comment

“Hoy, Johnny, still got that particle inna box?”
“Sure do, Jessie.”
“So where’s hit in there?”
“Me Pap says hit’s spread-out like but hit’s mostly inna middle.”
“Why’s hit spread then?”
“The more I taps the box, the wider hit spreads. Sommat to do wiff energy.”

Newton would have answered Jessie’s question by saying, sort of, “Pick a point anywhere in the box. The probability that the particle is at that point is equal to the probability that it’s at any other point.”

Quantum physicists take a different approach. They start by saying, “We know there’s zero probability that the particle is anywhere outside of the box, so there must be zero probability that it’s exactly at any wall.”

Now for a trick that we’re actually quite used to. When you listen to an orchestra, you can usually pick out the notes being played by a particular instrument. Someone blessed/cursed with perfect pitch can tell when a note is just a leetle bit flat, say an A being played at 438 cycles instead of 440. You can create any sound by mixing together the right frequencies in the right proportion. That’s how an MP3 recorder does it.

QM solutions use that strategy the other way round. They calculate probabilities by adding together sets of symmetric elementary shapes, all of which are zero at certain places, like the box walls. For instance, on average Johnnie’s particle will be near the middle of his box, so we start a set with an orange mound of probability right there. That mound is like our base frequency — it has no nodes, no non-wall places where the probability is zero.

Then we add a first overtone, the one-node yellow shape that represents equal probability on either side of a plane of zero probability.

Two nodal planes at right angles give us the four-peaked green shape. Further steps up have more and more nodal planes (cyan then blue, and so on). The video shows the running total up to 46 nodes.

.
As we add more nodes, the cumulative shape gets smoother and broader. After a huge number of steps, the sum will look pretty much like Newton’s (except for right at the walls, of course).

So if the classical and QM boxes wind up looking the same, why go to all that trouble? Because those nodes don’t come for free.

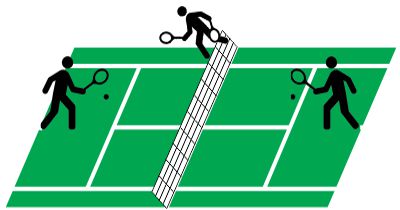Suppose you’re playing goalie in an inverse tennis game. There’s a player in each service box. Your job is to run the net line using your rackets to prevent either player from getting a ball into the opposing half-court. Basically, you want the ball’s locations to look like the single-node yellow shape up above. You’ll have to work hard to do that.

Now suppose they give you a second, crosswise net (the green shape). You’re going to have to work twice as hard. Now add a third net, and so on … each additional nodal plane is going to be harder (cost more energy) to keep empty. Not a problem if you have an infinite amount of energy.

Enter Planck and Einstein. They showed there’s a limit for small systems like atoms and molecules. Electrons dash about in atom- or molecule-shaped boxes, but the principle is the same. The total probability distribution is still the sum of bounded elementary shapes. However, you can’t use an infinite number of them. Rather, you start with the cheapest shapes (the fewest nodes) and build upward.

Tally two electrons for each shape you use. Why two? Because that’s the rule, no arguments.

It’s important to realize that QM does NOT say that two specific electrons occupy one shape. All the charge is spread out over all the shapes — we’re just keeping count.

When you run out of electrons the accumulated model shows everything we can know about the electronic configuration. You won’t know where any particular electron is, but you’ll know where some electron spends some time. For a chemist that’s the important thing — the peaks and nodes, the centers of negative and positive charge, are the most likely regions for chemical reactions to happen.

Johnnie’s energetic taps make his particle boldly go where no particle has gone before.

~~ Rich Olcott

Particles and Poetry

On May 2, 2016November 28, 2025 By rolcottIn Physics: Quantum Mechanics, UncategorizedLeave a comment

“Hoy, Johnny, wotcher got inna box?”
“Hit’s a particle, Jessie.”
“Ooo, lovely for you. Umm… wot’s a particle then?”
“Me Pap says hit’s sommat you calc’late about wiffout knowin’ wot ’tis.”

Pap’s right. Newton was a particle guy all the way (he was a strong supporter of the idea that light is composed of particles). One of his most important insights was that he could simplify gravitational calculations if he replaced an object with an equally massive “particle” located at the object’s center of mass. Could be a planet, or a moon, or that apple — he could treat each of them as a “particle.” That worked fine for his purposes, because the distances between his object centers were vastly larger than the object sizes.

Fleas — “Great fleas have little fleas upon their backs to bite ’em / And little fleas have lesser fleas and so on infinitum.” ~~ Augustus De Morgan

It took Roche to work out what happens when the distances get small. Gravitational forces break the original “particles” into littler particles. And when two of the little ones approach closely enough they break up, and then those break up… You get the idea. Take the process far enough and you get Saturn’s Rings, for instance.

But the analysis can keep going. Consider one “particle” in Saturn’s A-ring. It’s probably about 3″ across, made of ice, and contains something like 10²⁴ particles that happen to be molecules of H₂O. Each molecule contains 3 nuclei (2 protons and one oxygen nucleus) and 10 electrons, all 13 of which merit “particle” status if you’re calculating molecules. They’re all held together by a blizzard of photons carrying the electromagnetic forces between them. The oxygen nucleus contains 16 nuclear particles, each of which contains 3 quarks. The quark structures would fly apart except for a host of gluons that pass back and forth transmitting the nuclear strong force. Hooboy, do we got particles.

“Particle” is a slippery word. For Newton’s purposes, if an object is small relative to its distance from other objects, that was all he needed to know to treat it as a particle.

One dictionary specifies “a small localized object which has identifiable physical or chemical properties such as volume or mass.” However, there are theoretical grounds to believe that the classic “particle of light,” the photon, has neither mass nor volume. Physicists have had long arguments trying to devise a good working definition. Nobelist (1999) Gerard ‘t Hooft ended one such discussion by saying, “A particle is fundamental when it’s useful to think of it as fundamental.”

It may seem a little strange for a physicist to argue for imprecision. In fact, ‘t Hooft was arguing for a broad, even poetic but still precise understanding of the word.

Poets use metaphor to help us understand the world. Part of their art is to pack as much meaning as they can into the minimum number of words. In the same way, scientists use mathematics to pack observed relationships into a simile called an equation — a brief bit of math may connect and illuminate many disparate phenomena.

Think of physics as metaphor, with numbers.

Newton’s Law of Gravity works for for galaxies roving through a cluster and for basketball-sized satellites orbiting Earth and for stars circling a black hole (if they don’t get too close). Maxwell’s Equations, just 30 symbols including parentheses and equal signs, give the speed of light and describe the operation of electric motors. The particle physicists’ Standard Model makes predictions that match experimental results to more than a dozen decimal places.

Good equations are so successful that Nobelist (1963) Eugene Wigner wrote an influential paper entitled The Unreasonable Effectiveness of Mathematics in the Natural Sciences.

We sometimes get into trouble by confusing metaphor with reality. Poetic metaphors can be carried too far — Hamlet’s lungs were not in fact filling with water from his “sea of troubles.”

Mathematical models can also be carried too far. Popular (and practitioner) discussion of quantum mechanics is rife with over-extended metaphors. QM calculations yield only statistical results — an average position, say, plus or minus so much. It’s an average, but of what? The “many worlds” hypothesis is an unnecessarily long jump. There are simpler, less extravagant ways to account for statistical uncertainty.

~~ Rich Olcott

Hard Science Ain't Hard

Tag: Particle

The Ideal Gas Game

Fields of Dreams

The Thin Edge of Infinity

No-hair today, grown tomorrow

Abstract Horses

Think globally, act locally. Electrons do.

Location, Location, Location

Particles and Poetry