Category: Physics: Fundamentals

Competing Curves

On By rolcottIn Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

It’s still October but there’s a distinct taste of oncoming November in the air — grey, gusty with a moist chill as I step into Cal’s coffee shop. “You’re looking a bit grumpy, Cal.”

“Sure am, Sy. Some lady come in here, wanted pumpkin spice. The nerve! I sell good honest high‑quality coffee, special beans and everything, no goofy flavors. You want peppermint or apple brown betty, go down to the mermaid place. Here’s your mugfull, double‑dark as always. By the way, fair warning — Richard Feder’s in town and looking for you. He’s at that corner table.”

“Thanks, Cal.” <sound of footsteps> “Morning, Mr Feder. How’d things go in Fort Lee?

“Nicely, nicely… I got a question, Moire.”

“Of course you do.”

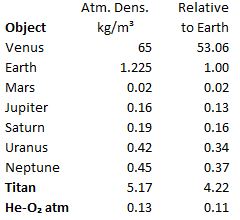
“I been reading your stuff, you had a graph in one post looks just like the graph in a different post. Here, I printed ’em out. What’s up with that?”

“But they plot entirely different things, brightness against distance in one, atom loss against time in the other, completely different equations.”

“Yeah, yeah, but the shapes are the same I don’t care you say they got different equations. Look, they even both go through the same points at x=2 and 4. What’re you trying to pull here?”

“Not pulling anything. Those two curves are similar, yes, but they’re not identical.” <quickly building charts on Old Reliable> “Here, I’ve laid them both on the same axis. For good measure I’ve extended the x‑axis into a second panel with a stretched‑out y‑axis. What do you see?”

“Well, the orange one goes up and stops but it looks like the blue one’s headed for the sky.”

“It is. But where on the x-axis do those things happen?”

“Zero and one. Okay so the blue line squoze in a little.”

“How about out there at the x=8 end? Looks like they’re close, I’ll grant you, but check the y‑values at at the left of the second panel.”

“Uhh… Looks like blue’s four times higher than orange. Then the orange line flattens out but the blue line not so much.”

“Mm‑hm. So they behave differently at that end, too.”

“Yeah, but what about in the middle here” <jabs finger at Old Reliable’s screen> “where they’re real close and even cross over each other a couple times and you could just draw a straight line?”

“You’ve put your finger on something that challenges every theoretician and research experimentalist who works in a quantitative field. How do you connect the dots? Sure, you can eyeball a straight line through observed points sometimes, there are even statistical techniques for locating the best possible straight line, but is a straight line even appropriate? Sometimes it is, sometimes it’s not, and often we don’t know.”

“How can you not know? Everything starts with a straight line, shortest distance between two points, right?”

“Only if they’re the right points. Real observations are always uncertain. Lenses are never perfect, adjustment screws have a little bit of play, detector pixels are larger than a perfect point would be, whatever. Good experimentalists put enormous amounts of time and care into eliminating or at least controlling for every imaginable error source, but perfect measurements just don’t happen.”

“So it’ll be a fuzzy straight line.”

“For some range of ‘fuzzy’, mm‑hm. Now we get into the theory issues. We’ve already seen the simplest one — range of validity. Your straight‑line approximation might be good enough for some purposes in the x‑range between 2 and 4, but things get out of hand outside of that range.”

“Okay, in graphs. But these two curves both look good. Why choose one over the other?”

“That’s where theory and data collude. Sometimes theories tell us what data to look for, sometimes the data challenges us to develop an explanatory theory, sometimes we just try curve after curve until we find one that works across the full range that experiment can reach but we don’t know why. What’s exciting is when we get to use the data to determine which of several competing theories is the correct one. Or least incorrect.”

“I got other ways to get excited.”

“Of course you do.”

~~ Rich Olcott

To Fly on Another World

On By rolcottIn Astronomy: Planetary Science, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

“Uncle Sy, why is PV=nRT the Ideal Gas Equation? Is it because it’s so simple but makes sense anyway?”

“It is ideal that way, Teena, but it’s simply an equation about gases that are ideal. Except there aren’t any. Real gases come close but don’t always follow the rule.”

“Why not? Are they sneaky?”

“Your kind of question. We like to think of gas particles as tiny ping‑pong balls that just bounce off of each other like … ping‑pong balls. That’s mostly true most of the time for most kinds of gas. One exception has to do with stickiness. Water’s one of the worst cases because its H2O molecules like to chain up. When two H2Os collide, if they’re pointed in the right directions they share a hydrogen atom like a bridge and stick together. If that sort of stickiness happens a lot then the quantity measure n acts like it’s less than we’d expect. That makes the PV product smaller.”

“I bet that doesn’t happen much when the gas is really hot. Two particles might stick and then BANG! another particle hits ’em and breaks it up!”

“Good thinking and that’s true. But there’s another kind of exception that holds even at high temperatures. A well‑behaved gas is mostly empty space because the ping‑pong balls are far apart unless they’re actually colliding. But suppose you squeeze out nearly all of the empty space and then try to squeeze some more.”

“Oh! The pressure gets even bigger than the equation says it should because you can’t squeeze the particles any smaller than they are, right?”

“Exactly.”

“Well, if the equation has these problems, why do we even use it at all?”

“Because it’s good enough, enough of the time, and we know when not to use it. I’ll give you an example. One of my clients wanted to know air density at ground level on Saturn’s moon Titan and all the planets that have an atmosphere.” <showing Old Reliable’s screen> “I found the planet data I needed in NASA’s Planetary Science website, but I had to do my own calculation for Titan. The pressure’s not crazy high and the temperature’s chilly but not quite cold enough to liquify nitrogen so the situation’s in‑range for the Ideal Gas Equation.”

“What’s a Pa?”

“That’s the symbol for a pascal, the unit of pressure. kPa is kilopascals, just like kg is kilograms. Earth’s atmospheric pressure is about 100 kPa.”

“Reliable says Wikipedia says Titan’s air is mostly nitrogen like Earth’s air is. Titan’s just a moon so it has to be smaller than Earth so its gravity must be smaller, too. Why is its atmosphere so much denser?”

“The cold. Titan’s air is 200 kelvins colder than Earth’s average temperature. You’re right, an individual gas particle feels a smaller pull of gravity on Titan, but it doesn’t have much kinetic energy to push its neighbors away so they all crowd closer together.”

“Why in the world does your client want to know that density number?”

“Clients rarely give me reasons. I suspect this has to do with designing a Titan‑explorer aircraft.”

“Ooo! Wait, what does that have to do with air density?”

“It has to do with how hard the machine has to work to push itself up. It’ll probably have horizontally spinning blades that push the air downwards, like helicopters do. With a setup like that, the lift depends on the blade’s length, how fast it’s spinning, and how dense the air is. If the air is dense, like on Titan, the designers can get the lifting thrust they need with short blades or a slow spin. On Mars the density’s only 2% of Earth’s so Ingenuity‘s rotors were 4 feet across and spun about ten times faster than they’d have to on Earth.”

“What about on our helium‑oxygen Earth?”

“That’s pretty much the same calculation. Give me a sec.” <tapping on Old Reliable’s screen> “Gas density would be a tenth of Earth’s, but a HeO‑copter would have to work against full‑Earth gravity. Huge blades rotating at supersonic speeds. Probably not a practical possibility.”

“Aw.”

“Yeah.”

~ Rich Olcott

Concept art for Titan Dragonfly
Credit: Steve Gribben/NASA/Johns Hopkins APL

The Ideal Gas Game

On By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Fundamentals, UncategorizedLeave a comment

“But Uncle Sy, you never did answer my real question!”

“What question was that, Teena?”

“About the helium planet. With oxygen. Oh, I guess I never did get around to asking that part of it. You side‑tracked us into how a helium‑oxygen atmosphere would be unstable unless it was really cold or the planet had more gravity than Earth so the helium wouldn’t fly away. But what I wanted to know was, what would it be like before the helium left? Like, could we fly a plane there?”

“Mmm, let’s get a leetle more specific. You asked about swapping all of Earth’s atmospheric nitrogen with helium. Was that one helium atom for each nitrogen molecule or each nitrogen atom?”

“What difference would that make?”

“Mass, to begin with. A helium atom weighs about 1/3 of a nitrogen atom, 1/7 of a nitrogen molecule. The atmospheric pressure we feel is the weight of all the air molecules above us. Swap out 80% of those molecules for something lighter, pressure goes down whether we swap helium for molecules or helium for atoms. We could calculate either one. But the change would be much harder to calculate for the atom‑for‑atom swap.”

“Why?”

“Mmm, have you gotten into equations yet in school?”

“You mean algebra, like 3x+7=8x+2? Yeah, they’re super‑easy.”

“This won’t even be as complicated as that. Here’s a famous Physics equation called The Ideal Gas Law — PV=nRT. Each letter stands for one quantity. Two adjacent quantities are multiplied together, okay? The pressure in a container is P, the container’s volume is V, T is the absolute temperature, and n is a measure of how much gas is in there.”

“You skipped R.”

“Yes, I did. It’s a constant number. Its job is to make all the units come out right. For instance, if the pressure’s in atmospheres, the volume’s in liters, n is in grams of helium and the temperature is in kelvins, then R is 0.021. Suppose you’re holding a balloon filled with helium and it’s at room temperature. What can you say about the gas?”

“Umm, all the nRT stuff doesn’t change so P times V, whatever it is, doesn’t change either.”

“If we let it fly upward until the pressure was only half what it is here…?”

“Then V would double. The balloon would get twice as big. Unless it burst, right?”

“You got the idea. Okay, now let’s fiddle with the right-hand side. Suppose we double the amount of helium.”

“P times V must get bigger but we don’t know which one.”

“Why not both?”

“Wooo… Each one could get some bigger… Oh, wait, I’m holding the balloon so the pressure’s not going to change so the balloon gets twice bigger.”

“Good thinking. One more thing and we can get back to your difference question. The Ideal Gas Law doesn’t care what kind of gas you’re working with. All the n quantity really cares about is how many particles are in the gas. A particle can be anything that moves about independently of anything else — helium atom or nitrogen molecule, doesn’t matter. If you change the definition of what n is measuring, all that happens is you have to adjust R so the units come out right. Then the equation works fine. Next step—”

“Wait, Uncle Sy, I want to think this atom‑or‑molecule thing through for myself. I’m gonna ignore R times T because both of them stay the same. So if we swap one atom of helium for one molecule of nitrogen, the number of particles doesn’t change and PV doesn’t change. But if we swap one atom of helium for each atom of nitrogen then n doubles and so does PV. But if we do that for the whole atmosphere then we can’t say that the pressure won’t change because the atmosphere could just expand and that’s the V but the pressures are all different as you go higher up anyway. Oh, wait, T changes, too, because it’s cold up there. It’s complicated, isn’t it?”

“It certainly is. Can we stick to just the simple atom‑for‑molecule swap?”

“Uh‑huh.”

~~ Rich Olcott

  • Thanks again, Xander, and happy birthday. Your question was deeper than I thought.

The Frame Game

On By rolcottIn Physics: Einstein, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

A familiar footstep outside my office, “C’mon in, Vinnie, the door’s open.”

“Hi, Sy, how ya doin’?”

“Can’t complain. Yourself?”

“Fine, fine. Hey, I been thinking about something you said while Al and us were talking about rockets and orbits and such. You remember that?”

“We’ve done that in quantity. What statement in particular?”

“It was about when you’re in the ISS, you still see like 88% of Earth’s gravity. But I seen video of those astronauts just floating around in the station. Seems to me those two don’t add up.”

“Hah! We’re talking physics of motion here. What’s the magic word?”

“You’re saying it’s frames? I thought black holes did that.”

“Black holes are an extreme example, but frame‑thinking is an essential tool in analyzing any kind of relative motion. Einstein’s famous ‘happy thought‘ about a man in a free‑falling elevator—”

“Whoa, why is that a happy thought? I been nervous about elevators ever since that time we got stuck in one.”

“At least it wasn’t falling, right? Point is, the elevator and whoever’s in it agree that Newton’s First Law of Motion is valid for everything they see in there.”

“Wait, which Law is that?”

“‘Things either don’t move or else they move at a steady pace along a straight line.’ Suppose you’re that guy—”

“I’d rather not.”

“… and the elevator is in a zero‑gravity field. You take something out of your pocket, put it the air in front of you and it stays there. You give it a tap and it floats away in a straight line. Any different behavior means that your entire frame — you, the elevator and anything else in there — is being accelerated by some force. Let’s take two possibilities. Case one, you and the elevator are resting on terra firma, tightly held by the force of gravity.”

“I like that one.”

“Case two, you and the elevator are way out in space, zero‑gravity again, but you’re in a rocket under 1-g acceleration. Einstein got happy because he realized that you’d feel the same either way. You’d have no mechanical way to distinguish between the two cases.”

“What’s that mean, mechanical?”

“It excludes sneaky ways of outside influence by magnetic fields and such. Anyhow, Einstein’s insight was key to extending Newton’s First Law to figuring acceleration for an entire frame. Like, for instance, an orbiting ISS.”

“Ah, you’re saying that floating astronauts in an 88% Earth-gravity field is fine because the ISS and the guys share the frame feeling that 88% but the guys are floating relative to that frame. But down here if we could look in there we’d see how both kinds of motion literally add up.”

“Exactly. It’s just much easier to think about only one kind at a time.”

“Wait. You said the ISS is being accelerated. I thought it’s going a steady 17500 miles an hour which it’s got to do to stay 250 miles up.”

“Is it going in a straight line?”

“Well, no, it’s going in a circle, mostly, except when it has to dodge some space junk.”

“So the First Law doesn’t apply. Acceleration is change in momentum, and the ISS momentum is constantly changing.”

“But it’s moving steady.”

“But not in a straight line. Momentum is a vector that points in a specific direction. Change the direction, you change the momentum. Newton’s Second Law links momentum change with force and acceleration. Any orbiting object undergoes angular acceleration.”

“Angular acceleration, that’s a new one. It’s degrees per second per second?”

“Yup, or radians. There’s two kinds, though — orbiting and spinning. The ISS doesn’t spin because it has to keep its solar panels facing the Sun.”

“But I’ve seen sci-fi movies set in something that spins to create artificial gravity. Like that 2001 Space Odyssey where the guy does his running exercise inside the ship.”

“Sure, and people have designed space stations that spin for the same reason. You’d have a cascade of frames — the station orbiting some planet, the station spinning, maybe even a ballerina inside doing pirouettes.”

“How do you calculate all that?”

“You don’t. You work with whichever frame is useful for what you’re trying to accomplish.”

“Makes my head spin.”

~~ Rich Olcott

The Threshold of Stuffiness

On By rolcottIn Chemistry, Physics: Fundamentals, UncategorizedLeave a comment

<chirp chirp> “Moire here.”

“Hi, Sy, it’s Susan Kim. I read your humidifier piece and I’ve got your answer for you.”

“Answer? I didn’t know I’d asked a question.”

“Sure you did. You worked out that your humidifier mostly keeps your office at 45% relative humidity by moisturizing incoming air that’s a lot drier than that. As a chemist I like how you brought in moles to check your numbers. Anyway, you wondered how to figure the incoming airflow. I’ve got your answer. It’s a scaling problem.”

“Mineral scaling? No, I don’t think so. The unit’s mostly white plastic so I wouldn’t see any scaling, but it seems to be working fine. I’ve been using de-ionized water and following the instructions to rinse the tank with vinegar every week or so.”

“Nope, not that kind of scale, Sy. You’ve got a good estimate from a small sample and you wondered how to scale it up, is all.”

“Sample? How’d I take a sample?”

“You gave us the numbers. Your office is 1200 cubic feet, right, and it took 88 milliliters of water to raise the relative humidity to where you wanted it, right, and the humidifier used a 1000 milliliters of water to keep it there for a day, right? Well, then. If one roomful of air requires 88 milliliters, then a thousand milliliters would humidify (1000/88)=11.4 room changes per day.”

“Is that a good number?”

“I knew you’d ask. According to the ventilation guidelines I looked up, ‘Buildings occupied by people typically need between 5 and 10 cubic feet per minute per person of fresh air ventilation.‘ You’re getting 11.4 roomfuls per day, times your office volume of 1200 cubic feet, divided by 1440 minutes per day. That comes to 9.5 cubic feet per minute. On the button if you’re alone, a little bit shy if you’ve got a client or somebody in there. I’d say your building’s architect did a pretty good job.”

“I like the place, except for when the elevators act up. All that figuring must have you thirsty. Meet me at Al’s and I’ll buy you a mocha latte.”

“Sounds like a plan.”

“Hi, folks. Saw you coming so I drew your usuals, mocha latte for Susan, black mud for Sy. Did I guess right?”

“Al, you make mocha lattes better than anybody.”

“Thanks, Susan, I do my best. Go on, take a table.”

“Susan, I was thinking while I walked over here. My cousin Crystal doesn’t like to wear those N95 virus masks because she says they make her short of breath. Her theory is that they trap her exhaled CO2 and those molecules get in the way of the O2 molecules she wants to breathe in. What does chemistry say to that theory?”

“Hmm. Well, we can make some estimates. N95 filtration is designed to block 95% of all particles larger than 300 nanometers. A couple thousand CO2 molecules could march abreast through a mesh opening that size no problem. An O2 molecule is about the same size. Both kinds are so small they never contact the mesh material so there’s essentially zero likelihood of differential effect.”

“So exhaled CO2 isn’t preferentially concentrated. Good. How about the crowd‑out idea?”

“Give me a second. <tapping on phone> Not supported by the numbers, Sy. There’s one CO2 for every 525 O2‘s in fresh air. Exhaled air is poorer in O2, richer in CO2, but even there oxygen has a 4‑to‑1 dominance.”

“But if the mask traps exhaled air…”

“Right. The key number is the retention ratio, what fraction of an exhaled breath the mask holds back. A typical exhale runs about 500 milliliters, could be half that if you’ve got lung trouble, twice or more if you’re working hard. This mask looks about 300 milliliters just sitting on the table, but there’s probably only 100 milliliters of space when I’m wearing it. It’s just arithmetic to get the O2/CO2 ratio for each breathing mode, see?”

“Looks good.”

“Even a shallow breather still gets 79 times more O2 than CO2. Blocking just doesn’t happen.”

“I’ll tell Crys.”

~ Rich Olcott

Which Way Is Up?

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

“OK, Moire, the Attitude Control System’s reaction wheels swing James Webb Space Telescope through whatever angle changes it wants, but how does ACS know what direction JWST‘s at to begin with? Does it go searching through that million‑star catalog to find something that matches?”

“Hardly, Mr Feder, that’d be way too much work for a shipboard computer. No, ACS consults the orientations maintained by a set of gyroscopes that are mounted on JWST‘s framework. Each one points along an unvarying bearing relative to the Universe, no matter how the satellite’s situated.”

“Gyroscopes? Like the one I had as a kid? Winding the string around the axle was a pain and then however hard I pulled the string I couldn’t keep one going for more than half a minute. It always wobbled anyway. Bad choice.”

“Not the JWST choice, NASA mostly doesn’t do toys. Actually, the gyroscope you remember has a long and honorable history. Gimbals have been known and used in one form or another for centuries. A few researchers mounted a rotor inside a gimbal set for various purposes in the mid‑1800s, but it was Léon Foucault who named his gadget a gyroscope when he used one for a public demonstration of the Earth’s rotation. People used to go to lectures like we go to a show. Science was popular in those days.”

“Wait — Foucault? The pendulum guy?”
 ”Wait — Foucault? The knife‑edge test guy?”

“Our science museum used to have a big pendulum. I loved to watch it knock down those domino thingies one by one as it turned around its circle. Then they took it out to make room for another dinosaur or something.”

“Yup. A museum’s most precious resource is floorspace. That weight swinging on a long wire takes up a lot of square feet. Foucault’s pendulum was another of his Earth‑rotation demonstrations, just a year after the gyroscope show. Yeah, Al, same guy — Foucault invented that technique you use to check your telescope mirrors. He pioneered a lot of Physics. He showed that the absorption spectrum of a gas when a light shines through it matches the spectrum it emits when you heat it up. His lightspeed measurement came within one percent of our currently accepted value. ”

Astronomer Cathleen shakes her head. “Imagine, 200 years after Kepler and Newton, yet people in Foucault’s day still needed convincing that the Earth is a globe floating in space. A century and a half later some still do. <sigh> Funny, isn’t it, how Foucault was working at the same time on two such different phenomena.”

“Not so different, Cathleen. Both demonstrate the same underlying principle — inertia relates to the Universe and doesn’t care about local conditions. Foucault was really working on inertia. He made use of two different inertial effects for his demonstrations. By the way, Mr Feder, the pendulum doesn’t turn. The Earth turns beneath the pendulum to bring those domino thingies into target position.”

“That’s hard to believe.”

“Could be why his demonstrations used two different phenomena. Given 19th Century technology, those were probably his best options.”

“If only he’d had lasers, huh?”

“One kind of modern gyroscope is laser‑based. Uses photons going around a ring. Actually, photons or pulses of them going around the same ring in opposite directions. When the ring itself rotates, the photons or pulses going against the rotation encounter the Start point sooner than their opposites do. Time the difference and you can figure the rotation rate. Unfortunately, Foucault didn’t have lasers or the exquisite timing devices we have today. But that’s not the kind of gyroscope JWST carries, anyway.”

“OK, I’ll bite. What does it use?”

“The slickest one yet, Al. If you carefully tap the rim of a good wine glass it’ll vibrate like the red line here. The dotted blue circle’s the glass at rest. Under the right conditions inertia holds the planes of vibration steady even if the glass itself rotates. People have figured out how to use that principle to build extremely accurate. reliable and low‑maintenance gyroscopes for measuring and stabilizing rotations. JWST carries a set.”

“Nothing to lubricate, eh?”

Portrait of Léon Foucault from Wikimedia under Creative Commons Attribution 3.0 Unported license.

~~ Rich Olcott

Symmetrical Eavesdropping

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

“Wait, Sy, you’ve made this explanation way more complicated than it has to be. All I asked about was the horrible whirling I’d gotten myself into. The three angular coordinates part would have done for that, but you dragged in degrees of freedom and deep symmetry and even dropped in that bit about ‘if measurable motion is defined.’ Why bother with all that and how can you have unmeasurable motion?”

“Curiosity caught the cat, didn’t it? Let’s head down to Eddie’s and I’ll treat you to a gelato. Your usual scoop of mint, of course, but I recommend combining it with a scoop of ginger to ease your queasy.”

“You’re a hard man to turn down, Sy. Lead on.”

<walking the hall to the elevators> “Have you ever baked a cake, Anne?”

“Hasn’t everyone? My specialty is Crazy Cake — flour, sugar, oil, vinegar, baking soda and a few other things but no eggs.”

“Sounds interesting. Well, consider the path from fixings to cake. You’ve collected the ingredients. Is it a cake yet?”

“Of course not.”

“Ok, you’ve stirred everything together and poured the batter into the pan. Is it a cake yet?”

“Actually, you sift the dry ingredients into the pan, then add the others separately, but I get your point. No, it’s not cake and it won’t be until it’s baked and I’ve topped it with my secret frosting. Some day, Sy, I’ll bake you one.”

<riding the elevator down to 2> “You’re a hard woman to turn down, Anne. I look forward to it. Anyhow, you see the essential difference between flour’s journey to cakehood and our elevator ride down to Eddie’s.”

“Mmm… OK, it’s the discrete versus continuous thing, isn’t it?”

“You’ve got it. Measuring progress along a discrete degree of freedom can be an iffy proposition.”

“How about just going with the recipe’s step number?”

“I’ll bet you use a spoon instead of a cup to get the right amount of baking soda. Is that a separate step from cup‑measuring the other dry ingredients? Sifting one batch or two? Those’d change the step‑number metric and the step-by-step equivalent of momentum. It’s not a trivial question, because Emmy Noether’s symmetry theorem applies only to continuous coordinates.”

“We’re back to her again? I thought—”

The elevator doors open at the second floor. We walk across to Eddie’s, where the tail‑end of the lunch crowd is dawdling over their pizzas. “Hiya folks. You’re a little late, I already shut my oven down.”

“Hi, Eddie, we’re just here for gelato. What’s your pleasure, Anne?”

“On Sy’s recommendation, Eddie, I’ll try a scoop of ginger along with my scoop of mint. Sy, about that symmetry theorem—”

“The same for me, Eddie.”

“Comin’ up. Just find a table, I’ll bring ’em over.”

We do that and he does that. “Here you go, folks, two gelati both the same, all symmetrical.”

“Eddie, you’ve been eavesdropping again!”

“Who, me? Never! Unless it’s somethin’ interesting. So symmetry ain’t just pretty like snowflakes? It’s got theorems?”

“Absolutely, Eddie. In many ways symmetry appears to be fundamental to how the Universe works. Or we think so, anyway. Here, Anne, have an extra bite of my ginger gelato. For one thing, Eddie, symmetry makes calculations a lot easier. If you know a particular system has the symmetry of a square, for instance, then you can get away with calculating only an eighth of it.”

“You mean a quarter, right, you turn a square four ways.”

“No, eight. It’s done with mirrors. Sy showed me.”

“I’m sure he did, Anne. But Sy, what if it’s not a perfect square? How about if one corner’s pulled out to a kite shape?”

“That’s called a broken symmetry, no surprise. Physicists and engineers handle systems like that with a toolkit of approximations that the mathematicians don’t like. Basically, the idea is to start with some nice neat symmetrical solution then add adjustments, called perturbations, to tweak the solution to something closer to reality. If the kite shape’s not too far away from squareness the adjusted solution can give you some insight onto how the actual thing works.”

“How about if it’s too far?”

“You go looking for a kite‑shaped solution.”

~~ Rich Olcott

Deep Symmetry

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

“Sy, I can understand mathematicians getting seriously into symmetry. They love patterns and I suppose they’ve even found patterns in the patterns.”

“They have, Anne. There’s a whole field called ‘Group Theory‘ devoted to classifying symmetries and then classifying the classifications. The split between discrete and continuous varieties is just the first step.”

“You say ‘symmetry‘ like it’s a thing rather than a quality.”

“Nice observation. In this context, it is. Something may be symmetrical, that’s a quality. Or it may be subject to a symmetry operation, say a reflection across its midline. Or it may be subject to a whole collection of operations that match the operations of some other object, say a square. In that case we say our object has the symmetry of a square. It turns out that there’s a limited number of discrete symmetries, few enough that they’ve been given names. Squares, for instance, have D4 symmetry. So do four-leaf clovers and the Washington Monument.”

“OK, the ‘4’ must be in there because you can turn it four times and each time it looks the same. What’s the ‘D‘ about?”

“Dihedral, two‑sided, like two appearances on either side of a reflection. That’s opposed to ‘C‘ which comes from ‘Cyclic’ like 1‑2‑3‑4‑1‑2‑3‑4. My lawn sprinkler has C4 symmetry, no mirrors, but add one mirror and bang! you’ve got eight mirrors and D4 symmetry.”

“Eight, not just four?”

“Eight. Two mirrors at 90° generate another one 45° between them. That’s the thing with symmetry operations, they combine and multiply. That’s also why there’s a limited number of symmetries. You think you’ve got a new one but when you work out all the relationships it turns out to be an old one looked at from a different angle. Cubes, for instance — who knew they have a three‑fold rotation axis along each body diagonal, but they do.”

“I guess symmetry can make physics calculations simpler because you only have to do one symmetric piece and then spread the results around. But other than that, why do the physicists care?”

“Actually they don’t care much about most of the discrete symmetries but they care a whole lot about the continuous kind. A century ago, a young German mathematician named Emmy Noether proved that within certain restrictions, every continuous symmetry comes along with a conserved quantity. That proof suddenly tied together a bunch of Physics specialties that had grown up separately — cosmology, relativity, thermodynamics, electromagnetism, optics, classical Newtonian mechanics, fluid mechanics, nuclear physics, even string theory—”

“Very large to very small, I get that, but how can one theory have that range? And what’s a conserved quantity?”

“It’s theorem, not theory, and it capped two centuries of theoretical development. Conserved quantities are properties that don’t change while a system evolves from one state to another. Newton’s First Law of Motion was about linear momentum as a conserved quantity. His Second Law, F=ma, connected force with momentum change, letting us understand how a straight‑line system evolves with time. F=ma was our first Equation of Motion. It was a short step from there to rotational motion where we found a second conserved quantity, angular momentum, and an Equation of Motion that had exactly the same form as Newton’s first one, once you converted from linear to angular coordinates.”

“Converting from x-y to radius-angle, I take it.”

“Exactly, Anne, with torque serving as F. That generalization was the first of many as physicists learned how to choose the right generalized coordinates for a given system and an appropriate property to serve as the momentum. The amazing thing was that so many phenomena follow very similar Equations of Motion — at a fundamental level, photons and galaxies obey the same mathematics. Different details but the same form, like a snowflake rotated by 60 degrees.”

“Ooo, lovely, a really deep symmetry!”

“Mm-hm, and that’s where Noether came in. She showed that for a large class of important systems, smooth continuous symmetry along some coordinate necessarily entails a conserved quantity. Space‑shift symmetry implies conservation of momentum, time‑shift symmetry implies conservation of energy, other symmetries lock in a collection of subatomic quantities.”

“Symmetry explains a lot, mm-hm.”

~~ Rich Olcott

Edged Things and Smooth Things

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, Uncategorized2 Comments

“Yeughh, Sy, that whirling, the entire Universe spinning around me in every direction at once.”

“Well, you were at a point of spherical symmetry, Anne.”

“There’s that word ‘symmetry‘ again. Right side matches left side, what else is there to say?”

“A whole lot, especially after the mathematicians and physicists started playing with the basic notion.”

“Which is?”

“Being able to execute a transformation without making a relevant difference.”

“Relevant?”

“To the context. Swapping the king of spades for the king of hearts would be relevant in some card games but not others, right? If it doesn’t affect the play or the scoring, swapping those two when no‑one’s looking would be a legitimate symmetry operation. Spin a snowflake 60° and it looks the same unless you care exactly where each molecule is. That’s rotational symmetry, but there’s lots of geometric symmetry operations — reflections, inversions, glides, translations—”

“Translation is a symmetry operation?”

“In this connection, ‘translation‘ means movement or swapping between two different places in space. The idea came from crystals. Think of a 3D checkerboard, except the borderlines aren’t necessarily perpendicular. Perfect crystals are like that. Every cube‑ish cell contains essentially the same arrangement of atoms. In principle you could swap the contents of any two cells without making a difference in any of the crystal’s measurable properties. That’d be a translation symmetry operation.”

“Glides make me think of ice skating.”

“The glide operation makes me think of a chess knight’s move — a translation plus a reflection across the translation path. Think of wet footprints crossing a dry floor. That’s one example of combining operations to create additional symmetries. You can execute 48 unique symmetry operations on a cube even without the translation‑related ones. In my grad school’s crystallography class they taught us about point group and wallpaper and space group symmetries. It blew me away — beautiful in both mathematical and artistic senses. You’ve seen M C Escher’s art?”

“Of course, I love it. I pushed into his studio once to watch him work but he spotted me and shouted something Dutch at me. I’ve wondered what he thought when I pushed out of there.”

“His pieces drew heavily on geometric symmetries. So did Baroque art, music and architecture.”

“Music? Oh, yes — they had motifs and whole sections you could swap, and rhythm patterns and tunes you could read forwards and backwards like in a mirror… We’ve come a long way from snowflake symmetry, haven’t we?”

“We’re just getting started. Here’s where the Physics folks generalized the idea. Your unfortunate experience in space is right on the edge of what most people consider as symmetry. Were you impressed with the cube’s 48 operations?”

“I suppose. I haven’t had time to think about it.”

“A sphere has an infinite number. You could pick any of an infinite number of lines through its center. Each is an axis for an infinite number of rotational symmetries. Times two because there’s an inversion point at the center so the rotation could go in either direction. Then each line is embedded in an infinite number of reflection planes.”

“Goodness, no wonder I was dizzy. But it’s still geometry. What was the edge that the physicists went past?”

“The border between step‑at‑a‑time discrete symmetries and continuous ones. Rotate that snowflake 60° and you’ve got a match; anything not a multiple of 60° won’t pair things up. Across the border, some of the most important results in modern Physics depend on continuous symmetries.”

“How can you even have a continuous symmetry?”

“Here, I’ll draw a circle on this square of paper. I can rotate the square by 90, 180 or 270 degrees and everything’s just the way it was. But if the square’s not relevant because we’re only interested in the circle, then I can rotate the paper by any amount I like and it’s a no‑difference transformation, right?”

“Continuous like on an infinite line but it’s wrapped around.”

“Exactly, and your infinite line is another example — any translation along that line, by a mile or a millimeter, is a perfectly good symmetry operation.”

“Ooo, and time, too. I experience time as an infinite line.”

“So does everyone. but most only travel in one direction.”

~~ Rich Olcott

Three Ways To Get Dizzy

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

<FZzzzzzzzzzzzzzzzzzzzzzzttt!> “Urk … ulp … I need to sit down, quick.”

“Anne? Welcome back, the couch is over there. Goodness, you do look a little green. Can I get you something to drink?”

“A little cool water might help, thanks.”

“Here. Just sit and breathe. That wasn’t your usual fizzing sound when you visit my office. When you’re ready tell me what happened. Must have been an experience, considering some of your other superpower adventures. Where did you ‘push‘ to this time?”

“Well, you know when I push forward I go into the future and when I push backward I go into the past. When I push up or down I get bigger or smaller. You figured out how pushing sideways kicks me to alternate probabilities. And then <shudder> there was that time I found a new direction to push and almost blew up the Earth.”

“Yes, that was a bad one. I’d think you’ve pretty well used up all the directions, though.”

“Not quite. This time I pushed outwards, the same in every direction.”

“Creative. And what happened?”

“Suddenly I was out in deep space, just tumbling in the blackness. There wasn’t an up or down or anything. I couldn’t even tell how big I was. I could see stars way off in the distance or maybe they were galaxies, but they were spinning all crazy. It took me a minute to realize it was me that was spinning, gyrating in several ways at once. It was scary and nauseating but I finally stopped part of it.”

“Floating in space with nothing to kill your angular momentum … how’d you manage to stabilize yourself at all?”

“Using my push superpower, of course. The biggest push resistance is against the past. I pulled pastward from just my shoulders and that stopped my nose‑diving but I was still whirling and cart‑wheeling. I tried to stop that with my feet but that only slowed me down and I was getting dizzy. My white satin had transformed into a spacesuit and I definitely didn’t want to get sick in there so I came home.”

“How’d you do that?”

“Oh, that was simple, I pulled inward. I had to um, zig‑zag? until I got just the right amount.”

“That explains the odd fizzing. I’m glad you got back. Looks like you’re feeling better now.”

“Mostly. Whew! So, Mr Physicist Sy, help me understand it all. <her voice that sounds like molten silver> Please?”

“Well. Um. There’s a couple of ways to go here. I’ll start with degrees of freedom, okay?”

“Whatever you say.”

“Right. You’re used to thinking in straight‑line terms of front/back, left/right and up/down, which makes sense if you’re on a large mostly‑flat surface like on Earth. In mathspeak each of those lines marks an independent degree of freedom because you can move along it without moving along either of the other two.”

“Like in space where I had those three ways to get dizzy.”

“Yup, three rotations at right angles to each other. Boatmen and pilots call them pitch, roll and yaw. Three angular degrees of freedom. Normal space adds three x-y-z straight‑line degrees, but you wouldn’t have been able to move along those unless you brought along a rocket or something. I guess you didn’t, otherwise you could have controlled that spinning.”

“Why would I have carried a rocket when I didn’t know where I was going? Anyhow, my push‑power can drive my straight‑line motion except I didn’t know where I was and that awful spinning had me discombobulated”

“Frankly, I’m glad I don’t know how you feel. Anyhow, if measurable motion is defined along a degree of freedom the measurement is called a coordinate. Simple graphs have an x-coordinate and a y-coordinate. An origin plus almost any three coordinates makes a coordinate system able to locate any point in space. The Cartesian x-y-z system uses three distances or you can have two distances and an angle, that’s cylindrical coordinates, or two angles and one distance and that’s polar coordinates.”

“Three angles?”

“You don’t know where you are.”

<shudder>
 <shudder>

~~ Rich Olcott