No-hair today, grown tomorrow

On May 15, 2017November 29, 2025 By rolcottIn Physics: Black Holes and Relativity, Physics: Quantum Mechanics, UncategorizedLeave a comment

It was a classic May day, perfect for some time by the lake in the park. I was watching the geese when a squadron of runners stampeded by. One of them broke stride, dashed my way and plopped down on the bench beside me. “Hi, Mr Moire. <pant, pant>”

“Afternoon, Jeremy. How are things?”

“Moving along, sir. I’ve signed up for track, I think it’ll help my base-running, I’ve met a new girl, she’s British, and that virtual particle stuff is cool but I’m having trouble fitting it into my black hole paper.”

“Here’s one angle. Nobelist Gerard ‘t Hooft said, ‘A particle is fundamental when it’s useful to think of it as fundamental.‘ In that sense, a black hole is a fundamental particle. Even more elementary than atoms, come to think of it.”

“Huh?”

“It has to do with the how few numbers you need to completely specify the particle. You’d need a gazillion terabytes for just the temperatures in the interior and oceans and atmosphere of Earth. But if you’re making a complete description of an isolated atom you just need about two dozen numbers — three for position, three for linear momentum, one for atomic number (to identify which element it represents), one for its atomic weight (which isotope), one for its net charge if it’s been ionized, four more for nuclear and electronic spin states, maybe three or four each for the energy levels of its nuclear and electronic configuration. So an atom is simpler than the Earth”

“And for a black hole?”

“Even simpler. A black hole’s event horizon is smooth, so smooth that you can’t distinguish one point from another. Therefore, no geography numbers. Furthermore, the physics we know about says whatever’s inside that horizon is completely sealed off from the rest of the universe. We can’t have knowledge of the contents, so we can’t use any numbers to describe it. It’s been proven (well, almost proven) that a black hole can be completely specified with only eleven numbers — one for its total mass-energy, one for its electric charge, and three each for position, linear momentum and angular momentum. Leave out the location and orientation information and you’ve got three numbers — mass, charge, and spin. That’s it.”

“How about its size or it temperature?”

“Depends how you measure size. Event horizons are spherical or nearly so, but the equations say the distance from an event horizon to where you’d think its center should be is literally infinite. You can’t quantify a horizon’s radius, but its diameter and surface area are both well-defined. You can calculate both of them from the mass. That goes for the temperature, too.”

“How about if it came from antimatter instead of matter?”

“Makes no difference because the gravitational stresses just tear atoms apart.”

“Wait, you said, ‘almost proven.’ What’s that about?”

“Believe it or not, the proof is called The No-hair Theorem. The ‘almost’ has to do with the proof’s starting assumptions. In the simplest case, zero change and zero spin and nothing else in the Universe, you’ve got a Schwarzchild object. The theorem’s been rigorously proven for that case — the event horizon must be perfectly spherical with no irregularities — ‘no hair’ as one balding physicist put it.”

“How about if the object spins and gets charged up, or how about if a planet or star or something falls into it?”

“Adding non-zero spin and charge makes it a Kerr-Newman object. The theorem’s been rigorously proven for those, too. Even an individual infalling mass has only a temporary effect. The black hole might experience transient wrinkling but we’re guaranteed that the energy will either be radiated away as a gravitational pulse or else simply absorbed to make the object a little bigger. Either way the event horizon goes smooth and hairless.”

“So where’s the ‘almost’ come in?”

“Reality. The region near a real black hole is cluttered with other stuff. You’ve seen artwork showing an accretion disk looking like Saturn’s rings around a black hole. The material in the disk distorts what would otherwise be a spherical gravitational field. That gnarly field’s too hairy for rigorous proofs, so far. And then Hawking pointed out the particle fuzz…”

~~ Rich Olcott

Gravity’s Real Rainbow

On February 20, 2017November 30, 2025 By rolcottIn Astronomy: Multi-messenger, Astronomy: Stellar Science, Gravitational astronomy, Physics: Black Holes and Relativity, Physics: Waves, UncategorizedLeave a comment

Some people are born to scones, some have scones thrust upon them. As I stepped into his coffee shop this morning, Al was loading a fresh batch onto the rack. “Hey, Sy, try one of these.”

“Uhh … not really my taste. You got any cinnamon ones ready?”

“Not much for cheddar-habañero, huh? I’m doing them for the hipster trade,” waving towards all the fedoras on the room. “Here ya go. Oh, Vinnie’s waiting for you.”

I navigated to the table bearing a pile of crumpled yellow paper, pulled up a chair. “Morning, Vinnie, how’s the yellow writing tablet working out for you?”

“Better’n the paper napkins, but it’s nearly used up.”

“What problem are you working on now?”

“OK, I’m still on LIGO and still on that energy question I posed way back — how do I figure the energy of a photon when a gravitational wave hits it in a LIGO? You had me flying that space shuttle to explain frames and such, but kept putting off photons.”

“Can’t argue with that, Vinnie, but there’s a reason. Photons are different from atoms and such because they’ve got zero mass. Not just nearly massless like neutrinos, but exactly zero. So — do you remember Newton’s formula for momentum?”

“Yeah, momentum is mass times the velocity.”

“Right, so what’s the momentum of a photon?”

“Uhh, zero times speed-of-light. But that’s still zero.”

“Yup. But there’s lots of experimental data to show that photons do carry non-zero momentum. Among other things, light shining on an an electrode in a vacuum tube knocks electrons out of it and lets an electric current flow through the tube. Compton got his Nobel prize for that 1923 demonstration of the photoelectric effect, and Einstein got his for explaining it.”

“So then where’s the momentum come from and how do you figure it?”

“Where it comes from is a long heavy-math story, but calculating it is simple. Remember those Greek letters for calculating waves?”

(starts a fresh sheet of note paper) “Uhh… this (writes λ) is lambda is wavelength and this (writes ν) is nu is cycles per second.”

“Vinnie, you never cease to impress. OK, a photon’s momentum is proportional to its frequency. Here’s the formula: p=h·ν/c. If we plug in the E=h·ν equation we played with last week we get another equation for momentum, this one with no Greek in it: p=E/c. Would you suppose that E represents total energy, kinetic energy or potential energy?”

“Momentum’s all about movement, right, so I vote for kinetic energy.”

“Bingo. How about gravity?”

“That’s potential energy ’cause it depends on where you’re comparing it to.”

“OK, back when we started this whole conversation you began by telling me how you trade off gravitational potential energy for increased kinetic energy when you dive your airplane. Walk us through how that’d work for a photon, OK? Start with the photon’s inertial frame.”

“That’s easy. The photon’s feeling no forces, not even gravitational, ’cause it’s just following the curves in space, right, so there’s no change in momentum so its kinetic energy is constant. Your equation there says that it won’t see a change in frequency. Wavelength, either, from the λ=c/ν equation ’cause in its frame there’s no space compression so the speed of light’s always the same.”

“Bravo! Now, for our Earth-bound inertial frame…?”

“Lessee… OK, we see the photon dropping into a gravity well so it’s got to be losing gravitational potential energy. That means its kinetic energy has to increase ’cause it’s not giving up energy to anything else. Only way it can do that is to increase its momentum. Your equation there says that means its frequency will increase. Umm, or the local speed of light gets squinched which means the wavelength gets shorter. Or both. Anyway, that means we see the light get bluer?”

“Vinnie, we’ll make a physicist of you yet. You’re absolutely right — looking from the outside at that beam of photons encountering a more intense gravity field we’d see a gravitational blue-shift. When they leave the field, it’s a red-shift.”

“Keeping track of frames does make a difference.”

Al yelled over, “Like using tablet paper instead of paper napkins.”

~~ Rich Olcott

Gettin’ kinky in space

On November 21, 2016November 28, 2025 By rolcottIn Astronomy: Planetary Science, Astronomy: Stellar Science, Physics: Newton and Gravity, UncategorizedLeave a comment

Things were simpler in the pre-Enlightenment days when we only five planets to keep track of. But Haley realized that comets could have orbits, Herschel discovered Uranus, and Galle (with Le Verrier’s guidance) found Neptune. Then a host of other astronomers detected Ceres and a host of other asteroids, and Tombaugh observed Pluto in 1930.

Astronomers relished the proliferation — every new-found object up there was a new test case for challenging one or another competing theory.

Here’s the currently accepted narrative… Long ago but quite close-by, there was a cloud of dust in the Milky Way galaxy. Random motion within it produced a swirl that grew into a vortex dozens of lightyears long.

Consider one dust particle (we’ll call it Isaac) afloat in a slice perpendicular to the vortex. Assume for the moment that the vortex is perfectly straight, the dust is evenly spread across it, and all particles have the same mass. Isaac is subject to two influences — gravitational and rotational.

making-a-solar-nebula — A kinked galactic cloud vortex,
out of balance and giving rise
to a solar system.

Gravity pulls Isaac towards towards every other particle in the slice. Except for very near the slice’s center there are generally more particles (and thus more mass) toward and beyond the center than back toward the edge behind him. Furthermore, there will generally be as many particles to Isaac’s left as to his right. Gravity’s net effect is to pull Isaac toward the vortex center.

But the vortex spins. Isaac and his cohorts have angular momentum, which is like straight-line momentum except you’re rotating about a center. Both of them are conserved quantities — you can only get rid of either kind of momentum by passing it along to something else. Angular momentum keeps Isaac rotating within the plane of his slice.

An object’s angular momentum is its linear momentum multiplied by its distance from the center. If Isaac drifts towards the slice’s center (radial distance decreases), either he speeds up to compensate or he transfers angular momentum to other particles by colliding with them.

But vortices are rarely perfectly straight. Moreover, the galactic-cloud kind are generally lumpy and composed of different-sized particles. Suppose our vortex gets kinked by passing a star or a magnetic field or even another vortex. Between-slice gravity near the kink shifts mass kinkward and unbalances the slices to form a lump (see the diagram). The lump’s concentrated mass in turn attracts particles from adjacent slices in a viscous cycle (pun intended).

After a while the lumpward drift depletes the whole neighborhood near the kink. The vortex becomes host to a solar nebula, a concentrated disk of dust whirling about its center because even when you come in from a different slice, you’ve still got your angular momentum. When gravity smacks together Isaac and a few billion other particles, the whole ball of whacks inherits the angular momentum that each of its stuck-together components had. Any particle or planetoid that tries to make a break for it up- or down-vortex gets pulled back into the disk by gravity.

That theory does a pretty good job on the conventional Solar System — four rocky Inner Planets, four gas giant Outer Planets, plus that host of asteroids and such, all tightly held in the Plane of The Ecliptic.

How then to explain out-of-plane objects like Pluto and Eris, not to mention long-period comets with orbits at all angles?

We now know that the Solar System holds more than we used to believe. Who’s in is still “objects whose motion is dominated by the Sun’s gravitational field,” but the Sun’s net spreads far further than we’d thought. Astronomers now hypothesize that after its creation in the vortex, the Sun accumulated an Oort cloud — a 100-billion-mile spherical shell containing a trillion objects, pebbles to planet-sized.

At the shell’s average distance from the Sun (see how tiny Neptune’s path is in the diagram) Solar gravity is a millionth of its strength at Earth’s orbit. The gravity of a passing star or even a conjunction of our own gas giants is enough to start an Oort-cloud object on an inward journey.

These trans-Neptunian objects are small and hard to see, but they’re revolutionizing planetary astronomy.

~~ Rich Olcott

Plutonic Goofyness

On November 14, 2016November 28, 2025 By rolcottIn Astronomy: Planetary Science, UncategorizedLeave a comment

goofy-and-dp-pluto — Is Pluto wearing a space helmet?
No, that helmet is Pluto.
(Based on a cartoon by Andy Diehl)

Andy Diehl brings up a question worth considering over a tasty beverage. How come Pluto’s a dog and Goofy’s a dog but Pluto gets the collar end of the leash? Hardly seems fair.

Which brings us to that other controversial Pluto, the one that NASA’s New Horizon spacecraft visited last July. (News flash — on 28 October, NASA announced that they’d received the very last of the data NH accumulated during that 2½-hour visit.) Official Astronomy has reclassified Pluto from “planet” to “dwarf planet,” but NH honcho Alan Stern and much of the rest of the world say, “No way!”

The traditionalist position is, “But we’ve always called Pluto the ninth planet.” Well, “always” only goes back to when the preternaturally persistent Clyde Tombaugh discovered the object in 1930. At the time he found it Pluto was indeed the ninth “planet” out from the Sun. However, it spends about 10% of each orbit* closer to the Sun than the eighth planet, Neptune. So should we call it the “seven-and-a-fraction-th” planet?

No, because (1) that contravenes Official Astronomy’s rules, and (2) it’d be silly.

So what are the rules for what’s a planet?

The object must be in orbit around its star.
The object must be massive enough to be rounded by its own gravity.
It must have cleared the neighborhood around its orbit.

“Rounded” is a bit tricky. It doesn’t mean “spherical” because if you spin a sphere, centrifugal forces move mass towards its equator. Earth’s equator is 13.3 miles further away from its center than its poles are. Miller’s Planet in the Interstellar movie is also a spheroid, even further deformed by elongation towards the black hole it orbits, yet it still rates as “rounded by its gravity” and qualifies as a planet.

“Clearing the neighborhood” means “my gravity dominates the motion of everything in my orbit.” Earth and Jupiter, both acknowledged planets, each have retinues of asteroids in the Trojan positions, at the same distance from the Sun as the host planet but in regions 60º ahead of or behind it. Even so, both planets often suffer messy encounters (remember Chicxulub and Chelyabinsk?) with asteroids and such that hadn’t gotten the memo.

Neptune meets all three criteria. Its gravity dominates Pluto’s motion even though Pluto’s in a separate orbit. For every three of Neptune’s trips around the Sun, Pluto makes exactly two. The gravitational converse doesn’t hold, though. Pluto’s mass is 0.1% of Neptune’s so the big guy doesn’t care.

This video, from an Orbits Table display at the Denver Museum of Nature and Science, shows a different Plutonian weirdness. We’re circling the Solar System at about 50 times Earth’s distance from the Sun (50 AU). Reading inward, the white lines represent the orbits of Neptune, Uranus, Saturn and Jupiter. The Asteroid Belt is the small greenish ring close to the Sun. The four terrestrial planets are even further in. The Kuiper Belt is the greenish ring that encloses the lot.

The yellow-orange line is Pluto’s orbit. Most of the Solar System lies within a thin pancake, the Plane of The Ecliptic. Pluto’s orbit is inclined 17º out of the Plane. That’s odd.

Theory says that the System evolved from an eddy in a primordial cloud of dust and gas. Gravity shrank that blob of stuff to form a disk at the eddy’s equator as it drew 99.9% of the system’s mass to form the Sun at the disk’s center.

Newton’s First Law is all about Conservation of Momentum. When applied to circular motion, it says that if you’re whirling in a certain plane, you’ll continue whirling in that plane unless something knocks you out of that plane. Hence, the Plane of The Ecliptic.

Pluto’s path is a puzzling challenge to the theory. It was only a minor puzzle until the 1990’s when astronomers discovered a plethora of Pluto-type objects outside of Neptune’s orbit. Most run way out of the Plane. Worst is Eris, at inclination 44º . Clearly, Pluto’s not special. It belongs to a large tribe that Astrophysicists must explain if they’re to claim to understand the Solar System.

~~ Rich Olcott

* – During its current 248-year orbit, Pluto was inside Neptune’s orbit between 1979 and 1999.

Reflections in Einstein’s bubble

On June 20, 2016November 28, 2025 By rolcottIn Mathematics: Dimensions, Physics: Black Holes and Relativity, Physics: Light and Relativity, Physics: Quantum Mechanics, UncategorizedLeave a comment

There’s something peculiar in this earlier post where I embroidered on Einstein’s gambit in his epic battle with Bohr. Here, I’ll self-plagiarize it for you…

Consider some nebula a million light-years away. A million years ago an electron wobbled in the nebular cloud, generating a spherical electromagnetic wave that expanded at light-speed throughout the Universe.

Last night you got a glimpse of the nebula when that lightwave encountered a retinal cell in your eye. Instantly, all of the wave’s energy, acting as a photon, energized a single electron in your retina. That particular lightwave ceased to be active elsewhere in your eye or anywhere else on that million-light-year spherical shell.

Suppose that photon was yellow light, smack in the middle of the optical spectrum. Its wavelength, about 580nm, says that the single far-away electron gave its spherical wave about 2.1eV (3.4×10^-19 joules) of energy. By the time it hit your eye that energy was spread over an area of a trillion square lightyears. Your retinal cell’s cross-section is about 3 square micrometers so the cell can intercept only a teeny fraction of the wavefront. Multiplying the wave’s energy by that fraction, I calculated that the cell should be able to collect only 10^-75 joules. You’d get that amount of energy from a 100W yellow light bulb that flashed for 10^-73 seconds. Like you’d notice.

But that microminiscule blink isn’t what you saw. You saw one full photon-worth of yellow light, all 2.1eV of it, with no dilution by expansion. Water waves sure don’t work that way, thank Heavens, or we’d be tsunami’d several times a day by earthquakes occurring near some ocean somewhere.

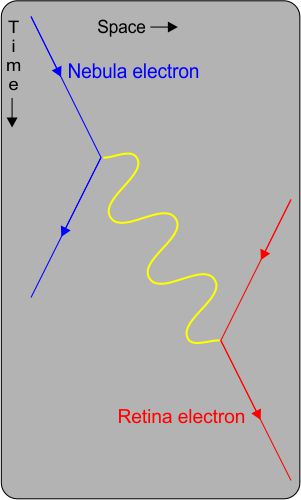Here we have a Feynman diagram, named for the Nobel-winning (1965) physicist who invented it and much else. The diagram plots out the transaction we just discussed. Not a conventional x-y plot, it shows Space, Time and particles. To the left, that far-away electron emits a photon signified by the yellow wiggly line. The photon has momentum so the electron must recoil away from it.

The photon proceeds on its million-lightyear journey across the diagram. When it encounters that electron in your eye, the photon is immediately and completely converted to electron energy and momentum.

Here’s the thing. This megayear Feynman diagram and the numbers behind it are identical to what you’d draw for the same kind of yellow-light electron-photon-electron interaction but across just a one-millimeter gap.

It’s an essential part of the quantum formalism — the amount of energy in a given transition is independent of the mechanical details (what the electrons were doing when the photon was emitted/absorbed, the photon’s route and trip time, which other atoms are in either neighborhood, etc.). All that matters is the system’s starting and ending states. (In fact, some complicated but legitimate Feynman diagrams let intermediate particles travel faster than lightspeed if they disappear before the process completes. Hint.)

Because they don’t share a common history our nebular and retinal electrons are not entangled by the usual definition. Nonetheless, like entanglement this transaction has Action-At-A-Distance stickers all over it. First, and this was Einstein’s objection, the entire wave function disappears from everywhere in the Universe the instant its energy is delivered to a specific location. Second, the Feynman calculation describes a time-independent, distance-independent connection between two permanently isolated particles. Kinda romantic, maybe, but it’d be a boring movie plot.

As Einstein maintained, quantum mechanics is inherently non-local. In QM change at one location is instantaneously reflected in change elsewhere as if two remote thingies are parts of one thingy whose left hand always knows what its right hand is doing.

Bohr didn’t care but Einstein did because relativity theory is based on geometry which is all about location. In relativity, change here can influence what happens there only by way of light or gravitational waves that travel at lightspeed.

In his book Spooky Action At A Distance, George Musser describes several non-quantum examples of non-locality. In each case, there’s no signal transmission but somehow there’s a remote status change anyway. We don’t (yet) know a good mechanism for making that happen.

It all suggests two speed limits, one for light and matter and the other for Einstein’s “deeper reality” beneath quantum mechanics.

~~ Rich Olcott

Is there stuff behind the stats?

On June 6, 2016November 28, 2025 By rolcottIn Physics: Quantum Mechanics, UncategorizedLeave a comment

It would have been awesome to watch Dragon Princes in battle (from a safe hiding place), but I’d almost rather have witnessed “The Tussles in Brussels,” the two most prominent confrontations between Albert Einstein and Niels Bohr.

The Tussles would be the Fifth (1927) and Seventh (1933) Solvay Conferences. Each conference was to center on a particular Quantum Mechanics application (“Electrons and Photons” and “The Atomic Nucleus,” respectively). However, the Einstein-Bohr discussions went right to the fundamentals — exactly what does a QM calculation tell us?

Einstein’s strength was in his physical intuition. By all accounts he was a good mathematician but not a great one. However, he was very good indeed at identifying important problems and guiding excellent mathematicians as he and they attacked those problems together.

Like Newton, Einstein was a particle guy. He based his famous thought experiments on what his intuition told him about how particles would behave in a given situation. That intuition and that orientation led him to paradoxes such as entanglement, the EPR Paradox, and the instantaneously collapsing spherical lightwave we discussed earlier. Einstein was convinced that the particles QM workers think about (photons, electrons, etc.) must in fact be manifestations of some deeper, more fine-grained reality.

Bohr was six years younger than Einstein. Both Bohr and Einstein had attained Directorship of an Institute at age 35, but Bohr’s has his name on it. He started out as a particle guy — his first splash was a trio of papers that treated the hydrogen atom like a one-planet solar system. But that model ran into serious difficulties for many-electron atoms so Bohr switched his allegiance from particles to Schrödinger’s wave theory. Solve a Schrödinger equation and you can calculate statistics like average value and estimated spread around the average for a given property (position, momentum, spin, etc).

Here’s where Ludwig Wittgenstein may have come into the picture. Wittgenstein is famous for his telegraphically opaque writing style and for the fact that he spent much of his later life disagreeing with his earlier writings. His 1921 book, Tractatus Logico-Philosophicus (in German despite the Latin title) was a primary impetus to the Logical Positivist school of philosophy. I’m stripping out much detail here, but the book’s long-lasting impact on QM may have come from its Proposition 7: “Whereof one cannot speak, thereof one must be silent.“

I suspect that Bohr was deeply influenced by the LP movement, which was all the rage in the mid-1920s while he was developing the Copenhagen Interpretation of QM.

An enormous literature, including quite a lot of twaddle, has grown up around the question, “Once you’ve derived the Schrödinger wave function for a given system, how do you interpret what you have?” Bohr’s Copenhagen Interpretation was that the function can only describe relative probabilities for the results of a measurement. It might tell you, for instance, that there’s a 50% chance that a particle will show up between here and here but only a 5% chance of finding it beyond there.

Following Logical Positivism all the way to the bank, Bohr denounced as nonsensical or even dangerously misleading any attachment of further meaning to a QM result. He went so far as to deny the very existence of a particle prior to a measurement that detects it. That’s serious Proposition 7 there.

I’ve read several accounts of the Solvay Conference debates between Einstein and Bohr. All of them agree that the conversation was inconclusive but decisive. Einstein steadfastly maintained that QM could not be a complete description of reality whilst Bohr refused to even consider anything other than inscrutable randomness beneath the statistics. The audience consensus went to Bohr.

None of the accounts, even the very complete one that I found in George Musser’s book Spooky Action at A Distance, provide a satisfactory explanation for why Bohr’s interpretation dominates today. Einstein described multiple situations where QM’s logic appeared to contradict itself or firmly established experimental results. However, at each challenge Bohr deflected the argument from Einstein’s central point to argue a subsidiary issue such as whether Einstein was denying the Heisenberg Uncertainty Principle.

Albert still stood at the end of the bouts, but Niels got the spectators’ decision on points. Did the ref make the difference?

~~ Rich Olcott

Think globally, act locally. Electrons do.

On May 16, 2016November 30, 2025 By rolcottIn Physics: Quantum Mechanics, UncategorizedLeave a comment

“Watcha, Johnnie, you sure ‘at particle’s inna box?”
“O’course ’tis, Jennie! Why wouldn’t it be?”
“Me Mam sez particles can tunnel outta boxes ’cause they’re waves.”
“Can’t be both, Jessie.”

Maybe it can.

Nobel-winning (1965) physicist Richard Feynman said the double-slit experiment (diagrammed here) embodies the “central mystery” of Quantum Mechanics.

When the bottom slit is covered the display screen shows just what you’d expect — a bright area opposite the top slit.

When both slits are open, the screen shows a banded pattern you see with waves. Where a peak in a top-slit wave meets a peak in the bottom-slit wave, the screen shines brightly. Where a peak meets a trough the two waves cancel and the screen is dark. Overall there’s a series of stripes. So electrons are waves, right?

But wait. If we throttle the beam current way down, the display shows individual speckles where each electron hits. So the electrons are particles, right?

Now for the spooky part. If both slits are open to a throttled beam those singleton speckles don’t cluster behind the slits as you’d expect particles to do. A speckle may appear anywhere on the screen, even in an apparently blocked-off region. What’s more, when you send out many electrons one-by-one their individual hits cluster exactly where the bright stripes were when the beam was running full-on.

It’s as though each electron becomes a wave that goes through both slits, interferes with itself, and then goes back to being a particle!

By the way, this experiment isn’t a freak observation. It’s been repeated with the same results many times, not just with electrons but also with light (photons), atoms, and even massive molecules like buckyballs (fullerene spheres that contain 60 carbon atoms). In each case, the results indicate that the whatevers have a dual character — as a localized particle AND as a wave that reacts to the global environment.

Physicists have been arguing the “Which is it?” question ever since Louis-Victor-Pierre-Raymond, the 7th Duc de Broglie, raised it in his 1924 PhD Thesis (for which he received a Nobel Prize in 1929 — not bad for a beginner). He showed that any moving “particle” comes along with a “wave” whose peak-to-peak wavelength is inversely proportional to the particle’s mass times its velocity. The longer the wavelength, the less well you know where the thing is.

I just had to put numbers to de Broglie’s equation. With Newton in mind, I measured one of the apples in my kitchen. To scale everything, I assumed each object moved by one of its diameters per second. (OK, I cheated for the electron — modern physics says it’s just a point, so I used a not-really-valid classical calculation to get something to work with.)

“Particle”	Mass, kilograms	Diameter, meters	Wavelength, meters	Wavelength, diameters
Apple	0.2	0.07	7.1×10^-33	1.0×10^-31
Buckyball	1.2×10^-24	1.0×10^-9	0.083	8.3×10⁺⁷
Hydrogen atom	1.7×10^-27	1.0×10^-10	600	6.0×10⁺¹²
Electron	9.1×10^-31	3.0×10^-17	3.7×10⁺¹²	1.2×10⁺²⁹

That apple has a wave far smaller than any of its hydrogen atoms so I’ll have no trouble grabbing it for a bite. Anything tinier than a small virus is spread way out unless it’s moving pretty fast, as in a beam apparatus. For instance, an electron going at 1% of light-speed has a wavelength only a nanometer wide.

Different physicists have taken different positions on the “particle or wave?” question. Duc de Broglie claimed that both exist — particles are real and they travel where their waves tell them to. Bohr and Heisenberg went the opposite route, saying that the wave’s not real, it’s only a mathematical device for calculating relative probabilities for measuring this or that value. Furthermore, the particle doesn’t exist as such until a measurement determines its location or momentum. Einstein and Schrödinger liked particles. Feynman and Dirac just threw up their hands and calculated.

Which brings us to the other kind of quantum spookiness — “entanglement.” In fact, Einstein actually used the word spukhafte (German for “spooky”) in a discussion of the notion. He really didn’t like it and for good reason — entanglement rudely collides with his own Theory of Relativity. But that’s another story.

~~ Rich Olcott

Smoke and a mirror

On February 8, 2016November 28, 2025 By rolcottIn General: Fun Stuff, Physics: Fundamentals, Uncategorized1 Comment

Grammie always grimaced when Grampie lit up one of his cigars inside the house. We kids grinned though because he’d soon be blowing smoke rings for us. Great fun to try poking a finger into the center, but we quickly learned that the ring itself vanished if we touched it.

My grandfather can’t take credit for the smoke ring on the left — it was “blown” by Mt Etna. Looks very like the jellyfish on the right, doesn’t it? When I see two such similar structures, I always wonder if the resemblance comes from the same physics phenomenon.

This one does — the physics area is Fluid Dynamics, and the phenomenon is a vortex ring. We need to get a little technical and abstract here: to a physicist a fluid is anything that’s composed of particles that don’t have a fixed spatial relationship to each other. Liquid water is a fluid, of course (its molecules can slide past each other) and so is air. The sun’s ionized protons and electrons comprise a fluid, and so can a mob of people and so can vehicle traffic (if it’s moving at all). You can use Fluid Dynamics to analyze motion when the individual particles are numerous and small relative to the volume in question.

Ring x-section — Adapted from a NOAA page

You get a vortex whenever you have two distinct fluids in contact but moving at sufficiently different velocities. (Remember that “velocity” includes both speed and direction.) When Grampie let out that little puff of air (with some smoke in it), his fast-moving breath collided with the still air around him. When the still air didn’t get out of the way, his breath curled back toward him. The smoke collected in the dark gray areas in this diagram.

That curl is the essence of vorticity and turbulence. The general underlying rule is “faster curls toward slower,” just like that skater video in my previous post. Suppose fluid is flowing through a pipe. Layers next to the outside surface move slowly whereas the bulk material near the center moves quickly. If the bulk is going fast enough, the speed difference will generate many little whorls against the circumference, converting pump energy to turbulence and heat. The plant operator might complain about “back pressure” because the fluid isn’t flowing as rapidly as expected from the applied pressure.

But Grampie didn’t puff into a pipe (he’s a cigar man, right?), he puffed into the open air. Those curls weren’t just at the top and bottom of his breath, they formed a complete circle all around his mouth. If his puff didn’t come out perfectly straight, the smoke had a twist to it and circulated along that circle, the way Etna’s ring seems to be doing (note the words In and Out buried in the diagram’s gray blobs). When a vortex closes its loop like that, you’ve got a vortex ring.

A vortex ring is a peculiar beast because it seems to have a life of its own, independent of the surrounding medium. Grampie’s little puff of vortical air usually retained its integrity and carried its smoke particles for several feet before energy loss or little fingers broke up the circulation.

To show just how special vortex rings are, consider the jellyfish. Until I ran across this article, I’d thought that jellyfish used jet propulsion like octopuses and squids do — squirt water out one way to move the other way. Not the case. Jellyfish do something much more sophisticated, something that makes them possibly “the most energy-efficient animals in the world.”

Thanks to a very nice piece of biophysics detective work (read the paper, it’s cool, no equations), we now know that a jellyfish doesn’t just squirt. Rather, it relaxes its single ring of muscle tissue to open wide. That motion pulls in a pre-existing vortex ring that pushes against the bell. On the power stroke, the jellyfish contracts its bell to push water out (OK, that’s a squirt) and create another vortex ring rolling in the opposite direction. In effect, the jellyfish continually builds and climbs a ladder of vortex rings.

Vortex rings are encapsulated angular momentum, potentially in play at any size in any medium.

~~ Rich Olcott

The Force(s) of Geometry

On February 1, 2016November 28, 2025 By rolcottIn Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

There’s a lot more to Geometry than congruent triangles. Geometry can generate hurricanes and slam you to the floor.

It all starts (of course) with Newton. His three laws boil down to

Effect is to Cause as Change of Motion is to Force.

They successfully account for the physical movement of pretty much everything bigger than an atom. But sometimes the forces are a bit weird and it takes Geometry to understand them.

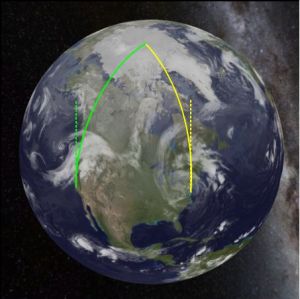For instance, suppose Fred and Ethel collaborate on a narwhale research project. Fred is based in San Diego CA and Ethel works out of Norfolk VA. They fly to meet their research vessel at the North Pole. Fred’s plane follows the green track, Ethel’s plane follows the yellow one. At the start of the trip, they’re on parallel paths going straight north (the dotted lines). After a few hours, though, Ethel notices the two planes pulling closer together.

Ethel calls on her Newton knowledge to explain the phenomenon. “It can’t be Earth’s gravity moving us together, because that force points down to Earth’s center and this is a sideways motion. Our planes each weigh about 2000 kilograms and we’re still 2,000 kilometers apart. By Newton’s F = G m₁m₂/r² equation, the gravitational force between us should be (6.7×10^-11 N m²/kg²) x (2000 kg) x (2000 kg) / (2,000 m)² = 6.7×10^-11 newtons, way too small to account for our speed of approach. Both planes were electrically grounded when we fueled up, so we’re both carrying a neutral electric charge and it can’t be an electrostatic force. If it were magnetic my compass would be going nuts and it’s not. Woo-hoo, I’ve discovered a new kind of force!”

See what I did there? Fred and Ethel would have stayed a constant distance apart if Earth were a cylinder. Parallel lines running up a cylinder never meet. But Earth is a sphere, not a cylinder. Any pair of lines on a sphere must meet, sooner or later. Ethel’s “sideways force” is a product of Geometry.

Hurricanes, too. This video shows a day in the life of Hurricane Sandy. Weather geeks will find several interesting details there, but for now just notice the centers of counter-clockwise rotation (the one off the Florida coast is Sandy). Storm centers in the Northern Hemisphere virtually always spin counterclockwise. Funny thing is, in the Southern Hemisphere those centers go clockwise instead.

The difference has to do with angular momentum. We could get all formal vector math here, but the easy way is to consider how fast the air is moving in different parts of the world.

We’ve all seen at least one ice show act where skaters form a spinning line. The last skater to join up (usually it’s a short girl) has to push like mad to catch the end of that moving line and everyone applauds her success. Meanwhile the tall girl at the center of the line is barely moving except to fend off dizziness.

The line rotates as a unit — every skater completes a 360^o rotation in the same time. Similarly, everywhere on Earth a day lasts for exactly 24 hours.

Skaters at the end of the line must skate faster than those further in because they have to cover a greater distance in the same amount of time. The same geometry applies to Earth’s atmosphere. The Earth is 25,000 miles around at the equator but only 12,500 miles around near the latitude of Whitehorse, Canada. By and large, a blob of air at the equator must move twice as fast as a blob at 60^o north.

Now suppose our speedy skater hits a slushy patch of ice. Her end of the line is slowed down, so what happens to the rest of the line? It deforms — there’s a new center of rotation that forces the entire line to curl around towards the slow spot. Similarly, that blob near the Equator in the split-Earth diagram curls in the direction of the slower-moving air to its north, which is counter-clockwise.

In the Southern hemisphere, “slower” is southward and clockwise.

If not for Geometry (those differing circle sizes), we wouldn’t have hurricanes. Or gravity — but that’s another story.

~~ Rich Olcott

And now for some completely different dimensions

On December 7, 2015November 28, 2025 By rolcottIn Mathematics: Dimensions, Physics: Fundamentals, UncategorizedLeave a comment

Terry Pratchett wrote that Knowledge = Power = Energy = Matter = Mass. Physicists don’t agree because the units don’t match up.

Physicists check equations with a powerful technique called “Dimensional Analysis,” but it’s only theoretically related to the “travel in space and time” kinds of dimension we discussed earlier.

It all started with Newton’s mechanics, his study of how objects affect the motion of other objects. His vocabulary list included words like force, momentum, velocity, acceleration, mass, …, all concepts that seem familiar to us but which Newton either originated or fundamentally re-defined. As time went on, other thinkers added more terms like power, energy and action.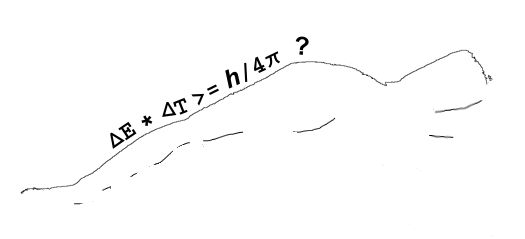

They’re all linked mathematically by various equations, but also by three fundamental dimensions: length (L), time (T) and mass (M). (There are a few others, like electric charge and temperature, that apply to problems outside of mechanics proper.)

Velocity, for example. (Strictly speaking, velocity is speed in a particular direction but here we’re just concerned with its magnitude.) You can measure it in miles per hour or millimeters per second or parsecs per millennium — in each case it’s length per time. Velocity’s dimension expression is L/T no matter what units you use.

Momentum is the product of mass and velocity. A 6,000-lb Escalade SUV doing 60 miles an hour has twice the momentum of a 3,000-lb compact car traveling at the same speed. (Insurance companies are well aware of that fact and charge accordingly.) In terms of dimensions, momentum is M*(L/T) = ML/T.

Acceleration is how rapidly velocity changes — a car clocked at “zero to 60 in 6 seconds” accelerated an average of 10 miles per hour per second. Time’s in the denominator twice (who cares what the units are?), so the dimensional expression for acceleration is L/T².

Physicists and chemists and engineers pay attention to these dimensional expressions because they have to match up across an equal sign. Everyone knows Einstein’s equation, E = mc². The c is the velocity of light. As a velocity its dimension expression is L/T. Therefore, the expression for energy must be M*(L/T)² = ML²/T². See how easy?

Now things get more interesting. Newton’s original Second Law calculated force on an object by how rapidly its momentum changed: (ML/T)/T. Later on (possibly influenced by his feud with Leibniz about who invented calculus), he changed that to mass times acceleration M*(L/T²). Conceptually they’re different but dimensionally they’re identical — both expressions for force work out to ML/T².

Something seductively similar seems to apply to Heisenberg’s Area. As we’ve seen, it’s the product of uncertainties in position (L) and momentum (ML/T) so the Area’s dimension expression works out to L*(ML/T) = ML²/T.

There is another way to get the same dimension expression but things aren’t not as nice there as they look at first glance. Action is given by the amount of energy expended in a given time interval, times the length of that interval. If you take the product of energy and time the dimensions work out as (ML²/T²)*T = ML²/T, just like Heisenberg’s Area.

It’s so tempting to think that energy and time negotiate precision like position and momentum do. But they don’t. In quantum mechanics, time is a driver, not a result. If you tell me when an event happens (the t-coordinate), I can maybe calculate its energy and such. But if you tell me the energy, I can’t give you a time when it’ll happen. The situation reminds me of geologists trying to predict an earthquake. They’ve got lots of statistics on tremor size distribution and can even give you average time between tremors of a certain size, but when will the next one hit? Lord only knows.

File the detailed reasoning under “Arcane” — in technicalese, there are operators for position, momentum and energy but there’s no operator for time. If you’re curious, John Baez’s paper has all the details. Be warned, it contains equations!

Trust me — if you’ve spent a couple of days going through a long derivation, totting up the dimensions on either side of equations along the way is a great technique for reassuring yourself that you probably didn’t do something stupid back at hour 14. Or maybe to detect that you did.

~~ Rich Olcott

Hard Science Ain't Hard

Tag: Momentum

No-hair today, grown tomorrow

Gravity’s Real Rainbow

Gettin’ kinky in space

Plutonic Goofyness

Reflections in Einstein’s bubble

Is there stuff behind the stats?

Think globally, act locally. Electrons do.

Smoke and a mirror

The Force(s) of Geometry

And now for some completely different dimensions