Tag: Newton

A Thumbtack in A Needlestack

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Light and Relativity, UncategorizedLeave a comment

“What’re the odds?”

“Odds on what, Vinnie?”

“A gazillion galaxies out there, only 41 lensing galaxy clusters, but one of them shows us a singleton star. I mean, what’s special about that star? What are the odds?”

I can’t help it. “Astronomical, Vinnie.”

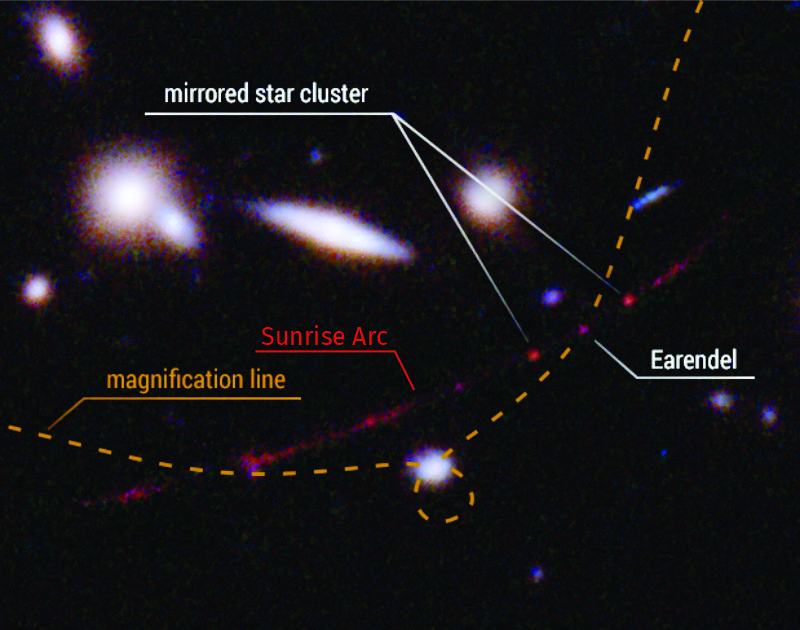
Cathleen punches my shoulder, hard. “Sy Moire, you be ashamed of yourself. That pun was ancient a century ago. Vinnie, the odds are better than they seem. We didn’t just stumble on Earendel and the Sunrise Arc, we found them in a highly targeted Big Data search for things just like that — objects whose light was extremely stretched and also gravitationally bent in our direction. The Arc’s lensing galaxy cluster has a spherical effect, more or less, so it also acts on light from other far-away objects and sends it in other directions. It even bends an image of our Milky Way towards Earendel’s galaxy.”

“I call weaseling — you used ‘more or less‘.”

“Guilty as charged, Vinnie. A nice, spherical black hole is the simplest case of gravitational lensing — just one mass at the center of its simple light‑bending gravity field. Same thing for a single star like our Sun. Clusters are messy. Tens or hundreds of billion‑star galaxies, scattered at random angles and random positions about their common center of mass. The combined gravity field is lumpy, to say the least. Half of that research paper is devoted to techniques for estimating the field and its effects on light in the region around the Arc.”

“I guess they had to get 3D positions for all the galaxies in the cluster. That’d be a lot of work.”

“It would, Al, but that’s beyond what current technology can do. Instead, they used computer models to do — get this, Sy — curve fitting.”

<chuckle> “Good one, Cathleen.”

“What’s so funny?”

“There’s a well-established scientific technique called ‘curve fitting.’ You graph some data and try to find an equation that does a respectable job of running through or at least near your data points. Newton started it, of course. Putting it in modern terms, he’d plot out some artillery data and say, ‘Hmm, that looks like a parabola H=h+v·t+a·t2. I wonder what values of h, v and a make the H-t curve fit those measurements. Hey, a is always 32 feet per second per second. Cool.’ Or something like that. Anyhow, Cathleen’s joke was that the researchers used curve fitting to fit the Sunrise Arc’s curve, right?”

“They did that, Sy. The underlying physical model, something called ‘caustic optics,’ says that—”

“Caustic like caustic soda? I got burnt by that stuff once.”

Image by Heiner Otterstedt,
under the Creative Commons Attribution-Share Alike 3.0 Unported license

“That’s the old name for sodium hydroxide, Vinnie. It’s a powerful chemical and yeah, it can give you trouble if you’re not careful. That name and caustic optics both come from the Greek word for burning. The optics term goes back to using a lens as a burning glass. See those focused patterns of light next to your water glass? Each pattern is a caustic. The Arc’s lensing cluster’s like any light‑bender, it’s enclosed in a caustic perimeter. Light passing near the perimeter gets split, the two parts going to either side of the perimeter. The Earendel team’s curve‑fitting project asked, ‘Where must the caustic perimeter be to produce these duplicate galaxy images neighboring the Arc?‘ The model even has that bulge from the gravity of a nearby foreground galaxy.”

“And the star?”

“Earendel seems to be smack on top of the perimeter. Any image touching that special line is intensified way beyond what it ought to be given the source’s distance from us. It’s a pretty bright star to begin with, though. Or maybe two stars.”

“Wait, you don’t know?”

“Not yet. This study pushed the boundaries of what Hubble can do for us. We’re going to need JWST‘s infrared instruments to nail things down.”

Al’s in awe. “Wow — that caustic’s sharp enough to pick one star out of a galaxy.”

“Beat the astronomical odds, huh?”

Adapted from a public-domain image.
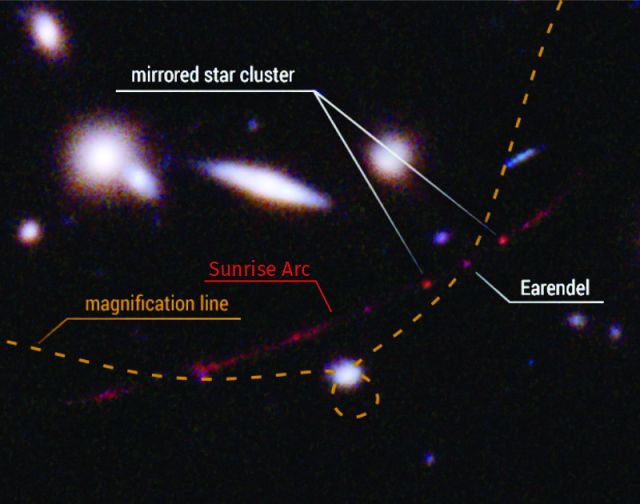
Credit: Science: NASA / ESA / Brian Welch (JHU) / Dan Coe (STScI); Image processing: NASA / ESA / Alyssa Pagan (STScI)

~~ Rich Olcott

Now And Then And There

On By rolcottIn Cosmology, James Webb Space Telescope, Physics: Light and Relativity, UncategorizedLeave a comment

Still at our table in Al’s otherwise empty coffee shop. We’re leading up to how Physics scrambled ‘Now‘ when a bell dings behind the counter. Al dashes over there. Meanwhile, Cathleen scribbles on a paper napkin with her colored pencils. She adds two red lines just as Al comes back with a plate of scones. “Here, Sy, if you’re going to talk Minkowski space this might be useful.”

“Hah, you’re right, Cathleen, this is perfect. Thanks, Al, I’ll have a strawberry one. Mmm, I love ’em fresh like this. OK, guys, take a look at Cathleen’s graphy artwork.”

“So? It’s the tile floor here.”

“Not even close, Mr Feder. Check the labels. The up‑and‑down label is ‘Time’ with later as higher. The diagram covers the period we’ve been sitting here. ‘Now‘ moves up, ‘Here’ goes side‑to‑side. ‘Table‘ and ‘Oven‘, different points in space, are two parallel lines. They’re lines because they both exist during this time period. They’re vertical because neither one moves from its relative spatial position. Okay?”

“Go on, Moire.”
  ”Makes sense to me, Sy.”

“Good. ‘Bell‘ marks an event, a specific point in spacetime. In this case it’s the moment when we here at the table heard the bell. I said ‘spacetime‘ because we’re treating space and time as a combined thing. Okay?”

“Go on, Moire.”
  ”Makes sense to me, Sy.”

“So then Al went to the oven and came back to the table. He traveled a distance, took some time to do that. Distance divided by time equals velocity. ‘Table‘ has zero velocity and its line is vertical. Al’s line would tilt down more if he went faster, okay?”

“Mmmm, got it, Sy.”
  ”Cute how you draw the come-back label backwards, lady. Go on, Moire.”

“I do my best, Mr Feder.”

“Fine, you’ve got the basic ideas. Now imagine all around us there’s graph paper like this — except there’s no paper and it’s a 4‑dimensional grid to account for motion in three spatial dimensions while time proceeds. Al left and returned to the same space point so his spacetime interval is just the time difference. If two events differ in time AND place there’s special arithmetic for calculating the interval.”

“So where’s that get us, Moire?”

“It got 18th and 19th Century Physics very far, indeed. Newton and everyone after him made great progress using math based on a nice stable rectangular space grid crossed with an orderly time line. Then Lorentz and Poincaré and Einstein came along.”

“Who’s Poincaré?”

“The foremost mathematician of nineteenth Century France. A mine safety engineer most days and a wide‑ranging thinker the rest of the time — did bleeding‑edge work in many branches of physics and math, even invented a few branches of his own. He put Lorentz’s relativity work on a firm mathematical footing, set the spacetime and gravity stage for Minkowsky and Einstein. All that and a long list of academic and governmental appointments but somehow he found the time to have four kids.”

Simultaneity Animation by “Acdx”
licensed under Creative Commons Attribution-Share Alike 4.0 International.

“A ball of fire, huh? So what’d he do to Newton’s jungle gym?”

“Turned its steel rod framework into jello. Remember how Cathleen’s Minkowski diagram connected slope with velocity? Einstein showed how Lorentz’s relativity factor sets a speed limit for our Universe. On the diagram, that’d be a minimum slope. Going vertical is okay, that’s standing still in space. Going horizontal isn’t, because that’d be instantaneous travel. This animation tells the ‘Now‘ story better than words can.”

“Whah?”
  ”Whah?”

“We’re looking down on three space travelers and three events. Speeds below lightspeed are within the gray hourglass shape. The white line perpendicular to each traveler’s time line is their personal ‘Now‘. The travelers go at different velocities relative to us so their slopes and ‘Now‘ lines are different. From our point of view, time goes straight up. One traveler is sitting still relative to us so its timeline is marked ‘v=0‘ and parallels ours. We and the v=0 traveler see events A, B and C happening simultaneously. The other travelers don’t agree. ‘Simultaneous‘ is an illusion.”

~~ Rich Olcott

Hyperbolic plane image by Murdock Grewar,
licensed under Creative Commons Attribution-Share Alike 4.0 International.

Now And Then

On By rolcottIn James Webb Space Telescope, Mathematics, Physics: Light and Relativity, UncategorizedLeave a comment

“Alright, I suppose there’s no going down below the Universe’s Year Zero, but what about the other direction? Do you physics guys have a handle on Time’s Top?”

“That’d be Cosmology, Mr Feder. We physicists avoid theorizing about stuff we can’t check against data. Well, except for string theory. The far past leaves clues that astronomers like Cathleen can gather. Sad to say, though, we barely have a handle on Now.”

Cathleen grins. Al and Mr Feder go, “Whaaat?”

“No, really. One of Einstein’s insights was that two observers randomly and independently flying through space won’t be able to agree on whether two external events occurred simultaneously. They can’t even agree on what time it is now.”

“Oh, yeah, I know about that. I’ve read about how the GPS system needs to make corrections to account for what relativity does to the satellite timings.”

“You’re right, Al, but that’s a different issue. Some of that relativistic correction has to do with space compression because of Earth’s mass. The simultaneity problem is strictly about rapid motion and geometry.”

“Wait — geometry?”

“Relativistic geometry, which is a bit different from the kind that Descartes built.”

“Whoa, Sy, slow down there. Descartes was the ‘I think therefore I am‘ guy, right? What’s that got to do with geometry?”

“I guess I got a little ahead of myself there, didn’t I? OK. Yeah, Al, same Descartes. Grew up Catholic in France, was a professional mercenary soldier in the Thirty Years War, wound up fighting first on the Catholic French side and later on fought on the Protestant Dutch side but cross‑over was common, both directions. He realized he was in an ostensibly religious war that was really about who ruled over whom. That may have had something to do with him becoming a professional philosopher who rejected all religious dogmas in favor of what he could learn solely from logic and his own senses. That’s where his famous mantra came from — he started by proving to himself that he existed.”

“Logic led to geometry, I suppose.”

“Indeed, but a new kind, one that required a few innovations that Descartes developed. On the one hand, mathematicians traditionally expressed algebraic problems in words and some of them were doozies, like saying ‘the zenzizenzizenzic‘ where we’d just say x8. We got that simple but <ahem> powerful notation from Descartes. On the geometry side, he’d ditch all the confusing line-ending markers in a diagram like this one. Instead, he’d label the whole line representing a known quantity with a front-of-the-alphabet letter like a or b or c. A line representing an unknown quantity would get its label from the alphabet-trailers like x, y and z. Then he used the same character conventions and his new power notation to write and manipulate algebraic expressions. Those notational inventions were foundational for his bridge between algebraic and geometrical problems. Draw your problem with lines and curves, transform it to algebraic equations, solve that problem exactly, transform it back to geometry and you’re done. Or vice-versa.”

The mesolabe instrument (in red).

“That goes back to Descartes, huh?”

“Mm-hm. His big innovation, though, arose from a borrow from an early Greek gadget called a mesolabe. He proposed an idealized version that would let someone break a line into exact fractions or compare a length against a unit length. That broke the rules of classical Geometry but setting his mesolabe’s Y‑angle to 90° prompted him to name points by their distance along the x– and y‑axes. That’s the nub of the Cartesian coordinate system — a rectangular grid of numbered straight lines that go on forever. Graph paper, right? Wrap the grid around the Earth and you’ve got latitudes and longitudes. Add more numbered grid lines perpendicular to either grid and you’ve got z‑axis coordinates. Three coordinates let you name any point in space. Newton and all the physicists who came after him until the dawn of the 20th Century assumed Descartes’ nice, stable coordinate system.”

“20th Century — that’s when Einstein came on the scene. He broke that system?”

“Sure did. You’ve heard about bent space?”

“Who hasn’t?”

“Well, fasten your seat belts, it’s going to be a fun ride.”

~~ Rich Olcott

The Bottom of Time

On By rolcottIn Astronomy: Techniques, Cosmology, James Webb Space Telescope, Uncategorized2 Comments

“Cathleen, one of my Astronomy magazines had an article, claimed that James Webb Space Telescope can see back to the Big Bang. That doesn’t seem right, right?”

“You’re right, Al, it’s not quite right. By our present state of knowledge JWST‘s infrared perspective goes back only 98% of the way to the Bang. Not quite the Bottom of Time, but close.”

“Whaddaya mean, ‘Bottom of Time‘? I’ve heard people talking about how weird it musta been before the Big Bang. And how can JWST see back in time anyway? Telescopes look across space, not time.”

“So many questions, Mr Feder, and some hiding behind others. That’s his usual mode, Cathleen. Care to tag-team?”

“You’re on, Sy. Well, Mr Feder. The ‘look back in time‘ part comes from light not traveling infinitely fast. We’ve known that for three centuries, ever since Rømer—”

“Roamer?”

“Ole Rømer, a Danish scientist who lived in Newson’s time. Everyone knew that Jupiter’s innermost large moon Io had a dependably regular orbit, circling Jupiter every 49½ hours like clockwork. Rømer was an astronomer when he wasn’t tutoring the French King’s son or being Copenhagen’s equivalent of Public Safety Commissioner. He watched Io closely, kept notes on exactly when she ducked behind Jupiter and when she reappeared on the other side. His observed timings weren’t quite regular, generally off by a few minutes. Funny thing was, the irregularities correlated with the Earth‑Jupiter distance — up to 3½ minutes earlier than expected when Earth in its orbit was closest to Jupiter, similarly late when they were far apart. There was a lot of argument about how that could be, but Rømer, Huygens, even Newton, all agreed that the best explanation was that we only see Io’s passage events after light has taken its time to travel from there to here.”

“Seems reasonable. Why should people argue about that?”

“The major sticking point was the speed that Huygens calculated from Rømer’s data. We now know it’s 186000 miles or 300000 kilometers or one lightsecond per second. Different ways of stating the same quantity. Huygens came up with a somewhat smaller number but still. The establishment pundits had been okay with light transmission being instantaneous. Given definite numbers, though, they had trouble accepting the idea that anything physical could go that fast.”

“Tag, my turn. Flip that distance per time ratio upside down — for every additional lightsecond of distance we’re looking at events happening one second farther into the past. That’s the key to JWST‘s view into the long‑ago. Al, you got that JWST‘s infrared capabilities will beat Hubble‘s vis‑UV ones for distance. Unless there’s something seriously wrong with Einstein’s assumption that lightspeed’s an absolute constant throughout spacetime, we expect JWST to give us visibility to the oldest free photons in the Universe, just 379000 years upward from the Big Bang.”

“Wait, I heard weaseling there. Free photons? Like you gotta pay for the others?”

“Ha, ha, Mr Feder. During those first 379000‑or‑so years, we think the Universe was so hot and so dense that no photon’s wave had much of a chance to spread out before it encountered a charged something and got absorbed. At last, things cooled down enough for atoms to form and stay in one piece. Atoms are neutral. Quantum rules restrict their interaction to only photons that have certain wavelengths. The rest of the photons, and there’s a huge number of them, were free to roam the expanding Universe until they happen to find a suitable absorber. Maybe someone’s eye or if we’re lucky, a sensor on JWST or some other telescope.”

Thanks for this to George Derenburger

“What about before the 300‑and‑something thousand years? Like, before Year Zero? Musta been weird, huh?”

“Well, there’s a problem with that question. You’re assuming there was a Year Minus‑One, but that’s just not the case.”

“Why not? Arithmetic works that way.”

“But the Universe doesn’t. Stephen Hawking came up with a good way to think about it. What on Earth is south of the South Pole?”

“Eeayahh … nope. Can’t get any further south than that.”

“Well, there you are, so to speak. Time’s bottom is Year Zero and you can’t get any further down than that. We think.”

~~ Rich Olcott

Which Way Is Up?

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

“OK, Moire, the Attitude Control System’s reaction wheels swing James Webb Space Telescope through whatever angle changes it wants, but how does ACS know what direction JWST‘s at to begin with? Does it go searching through that million‑star catalog to find something that matches?”

“Hardly, Mr Feder, that’d be way too much work for a shipboard computer. No, ACS consults the orientations maintained by a set of gyroscopes that are mounted on JWST‘s framework. Each one points along an unvarying bearing relative to the Universe, no matter how the satellite’s situated.”

“Gyroscopes? Like the one I had as a kid? Winding the string around the axle was a pain and then however hard I pulled the string I couldn’t keep one going for more than half a minute. It always wobbled anyway. Bad choice.”

“Not the JWST choice, NASA mostly doesn’t do toys. Actually, the gyroscope you remember has a long and honorable history. Gimbals have been known and used in one form or another for centuries. A few researchers mounted a rotor inside a gimbal set for various purposes in the mid‑1800s, but it was Léon Foucault who named his gadget a gyroscope when he used one for a public demonstration of the Earth’s rotation. People used to go to lectures like we go to a show. Science was popular in those days.”

“Wait — Foucault? The pendulum guy?”
 ”Wait — Foucault? The knife‑edge test guy?”

“Our science museum used to have a big pendulum. I loved to watch it knock down those domino thingies one by one as it turned around its circle. Then they took it out to make room for another dinosaur or something.”

“Yup. A museum’s most precious resource is floorspace. That weight swinging on a long wire takes up a lot of square feet. Foucault’s pendulum was another of his Earth‑rotation demonstrations, just a year after the gyroscope show. Yeah, Al, same guy — Foucault invented that technique you use to check your telescope mirrors. He pioneered a lot of Physics. He showed that the absorption spectrum of a gas when a light shines through it matches the spectrum it emits when you heat it up. His lightspeed measurement came within one percent of our currently accepted value. ”

Astronomer Cathleen shakes her head. “Imagine, 200 years after Kepler and Newton, yet people in Foucault’s day still needed convincing that the Earth is a globe floating in space. A century and a half later some still do. <sigh> Funny, isn’t it, how Foucault was working at the same time on two such different phenomena.”

“Not so different, Cathleen. Both demonstrate the same underlying principle — inertia relates to the Universe and doesn’t care about local conditions. Foucault was really working on inertia. He made use of two different inertial effects for his demonstrations. By the way, Mr Feder, the pendulum doesn’t turn. The Earth turns beneath the pendulum to bring those domino thingies into target position.”

“That’s hard to believe.”

“Could be why his demonstrations used two different phenomena. Given 19th Century technology, those were probably his best options.”

“If only he’d had lasers, huh?”

“One kind of modern gyroscope is laser‑based. Uses photons going around a ring. Actually, photons or pulses of them going around the same ring in opposite directions. When the ring itself rotates, the photons or pulses going against the rotation encounter the Start point sooner than their opposites do. Time the difference and you can figure the rotation rate. Unfortunately, Foucault didn’t have lasers or the exquisite timing devices we have today. But that’s not the kind of gyroscope JWST carries, anyway.”

“OK, I’ll bite. What does it use?”

“The slickest one yet, Al. If you carefully tap the rim of a good wine glass it’ll vibrate like the red line here. The dotted blue circle’s the glass at rest. Under the right conditions inertia holds the planes of vibration steady even if the glass itself rotates. People have figured out how to use that principle to build extremely accurate. reliable and low‑maintenance gyroscopes for measuring and stabilizing rotations. JWST carries a set.”

“Nothing to lubricate, eh?”

Portrait of Léon Foucault from Wikimedia under Creative Commons Attribution 3.0 Unported license.

~~ Rich Olcott

Turn This Way to Turn That Way

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Newton and Gravity, Space Travel, UncategorizedLeave a comment

“I don’t understand, Sy. I get that James Webb Space Telescope uses its reaction wheels like a ship uses a rudder to change direction by pushing against something outside. Except the rudder pushes against water but the reaction wheels push against … what, the Universe?”

“Maybe probably, Al. We simply don’t know how inertia works. Newton just took inertia as a given. His Laws of Motion say that things remain at rest or persist in linear motion unless acted upon by some force. He didn’t say why. Einstein’s General Relativity starts from his Equivalence Principle — gravitational inertia is identical to mechanical inertia. That’s held up to painstaking experimental tests, but why it works is still an open question. Einstein liked Mach’s explanation, that we experience these inertias because matter interacts somehow with the rest of the Universe. He didn’t speculate how that interaction works because he didn’t like Action At A Distance. The quantum field theory people say that everything’s part of the universal field structure, which sounds cool but doesn’t help much. String theory … ’nuff said.”

“Hey, Moire, what’s all that got to do with the reaction wheel thing? JWST can push against one all it wants but it won’t go anywhere ’cause the wheel’s inside it. What’s magic about the wheels?”

“JWST doesn’t want to go anywhere else, Mr Feder. We’re happy with it being in its proper orbit, but it needs to be able to point to different angles. Reaction wheels and gyroscopes are all about angular momentum, not about the linear kind that’s involved with moving from place to place.”

“HAH! JWST is moving place to place, in that orbit! Ain’t it got linear momentum then?”

Newton’s Principia, Proposition II, Theorem II

“In a limited way, pun intended. Angular momentum is linear momentum plus a radial constraint. This goes back to Newton and his Principia book. I’ve got a copy of his basic arc‑splitting diagram here in Old Reliable. The ABCDEF line is a section of some curve around point S. He treated it as a succession of short line segments ABc, BCd, CDe and so on. If JWST is at point B, for instance, Newton would say that it’s traveling with a certain linear momentum along the BCd line. However, it’s constrained to move along the arc so it winds up at D instead d. To account for the constraint Newton invented centripetal force to pull along the Sd line. He then mentally made the steps smaller and smaller until the sequence of short lines matched the curve. At the limit, a sequence of little bits of linear momentum becomes angular momentum. By the way, this step‑reduction process is at the heart of calculus. Anyway, JWST uses its reaction wheels to swing itself around, not to propel itself.”

“And we’re back to my original question, Sy. What makes that swinging happen?”

“Oh, you mean the mechanical reality. Easy, Al. Like I said, three pairs of motorized wheels are mounted on JWST‘s frame near the center of mass. Their axles are at mutual right angles. Change a wheel’s angular momentum, you get an equal opposing change to the satellite’s. Suppose the Attitude Control System wants the satellite to swing to starboard. That’d be clockwise viewed from the cold side. ACS must tell a port/starboard motor to spin its wheel faster counterclockwise. If it’s already spinning clockwise, the command would be to put on the brakes, right? Either way, JWST swings clockwise. With the forward/aft motors and the hot‑side/cold‑side motors, the ACS is equipped to get to any orientation. See how that works?”

“Hang on.” <handwaving ensues> “Yeah, I guess so.”

“Hey, Moire. What if the wheel’s already spinning at top speed in the direction the ACS wants more of?”

“Ah, that calls for a momentum dump. JWST‘s equipped with eight small rocket engines called thrusters. They convert angular momentum back to linear momentum in rocket exhaust. Suppose we need a further turn to starboard but a port/starboard wheel is nearing threshold spin rate. ACS puts the brakes on that wheel, which by itself would turn the satellite to port. However, ACS simultaneously activates selected thrusters to oppose the portward slew. Cute, huh?”

~~ Rich Olcott

The Venetian Blind Problem

On By rolcottIn Astronomy: Planetary Science, Chemistry, Physics: Light and Relativity, UncategorizedLeave a comment

Susan Kim gives me the side‑eye. “Sy, I get real suspicious when someone shows me a graph with no axis markings. I’ve seen that ploy used too often by people pushing a bias — you don’t know what happens offstage either side and you don’t know whether an effect was large or small. Your animated chart was very impressive, how that big methane infrared absorption peak just happens to fill in the space between CO2 and H2O peaks. But how wide is the chart compared to the whole spectrum? Did you cherry‑pick a region that just happens to make your point?”

“Susan, how could you accuse me of such underhanded tactics? But I confess — you’re right, sort of. <more tapping on Old Reliable’s keyboard> The animation only covered the near‑IR wavelengths from 1.0 to 5.0 micrometers. Here’s the whole strip from 0.2 micrometers in the near UV, out to 70 micrometers in the far IR. Among other things, it explains the James Webb Space Telescope, right, Al?”

Spectrum of Earth’s atmosphere. Adapted
under the Creative Commons 3.0 license
from Robert Wohde’s work
with the HITRAN2004 spectroscopic database,

“I know the Webb’s set up for IR astronomy from space, Sy. Wait, does this graph say there’s too much water vapor blocking the galaxy’s IR and that’s why they’re putting the scope like millions of miles away out there?”

“Not quite. The mission designers’ problem was the Sun’s heat, not Earth’s water vapor. The solution was to use Earth itself to shield the device from the Sun’s IR emissions. The plan is to orbit the Webb around the Earth‑Sun L2 point, about a million miles further out along the Sun‑Earth line. Earth’s atmosphere being only 60 miles thick, most of it, the Webb will be quite safe from our water molecules. No, our steamy atmosphere’s only a problem for Earth‑based observatories that have to peer through a Venetian blind with a few missing slats at very specific wavelengths.”

“Don’t forget, guys, the water spectrum is a barrier in both directions. Wavelengths the astronomers want to look at can’t get in, but also Earth’s heat radiation at those wavelengths can’t get out. Our heat balance depends on the right amount of IR energy making it out through where those missing slats are. That’s where Sy’s chart comes in — it identifies the wavelengths under threat by trace gases that aren’t so trace any more.”

“And we’re back to your point, Susan. We have to look at the whole spectrum. I heard one pitch by a fossil fuel defender who based his whole argument on the 2.8‑micrometer CO2 peak. ‘It’s totally buried by water’s absorption,‘ he claimed. ‘Can’t possibly do us any further damage.’ True, so far as it goes, but he carefully ignored CO2‘s other absorption wavelengths. Pseudoscience charlatan, ought to be ashamed of himself. Methane’s not as strong an absorber as CO2, but its peaks are mostly in the right places to do us wrong. Worse, both gas concentrations are going up — CO2 is 1½ times what it was in Newton’s day, and methane is 2½ times higher.”

Data from EPA Climate Indicators Explorer

“Funny how they both go up together. I thought the CO2 thing was about humanity burning fossil fuels but you said methane operations came late to that game.”

“Right on both counts, Al. Researchers are still debating why methane’s risen so bad but I think they’re zeroing in on cow gas — belches and farts. By and large, industry has made the world’s population richer over the past two centuries. People who used to subsist on a grain diet can now afford to buy meat so we’ve expanded our herds. Better off is good, but there’s an environmental cost.”

Al gets a far-away look. “Both those gases have carbon in them, right? How about we burn methane without the carbon in, just straight hydrogen?”

Susan gets excited. “Several groups in our lab are working on exactly that possibility, Al. The 2H2+O2→2H2O reaction yields 30% more energy per oxygen atom than burning methane. We just need to figure out how to use hydrogen economically.”

~~ Rich Olcott

Maybe It’s Just A Coincidence

On By rolcottIn Crazy Theories, Physics: Black Holes and Relativity, UncategorizedLeave a comment

Raucous laughter from the back room at Al’s coffee shop, which, remember, is situated on campus between the Physics and Astronomy buildings. It’s Open Mic night and the usual crowd is there. I take a vacant chair which just happens to be next to the one Susan Kim is in. “Oh, hi, Sy. You just missed a good pitch. Amanda told a long, hilarious story about— Oh, here comes Cap’n Mike.”

Mike’s always good for an offbeat theory. “Hey, folks, I got a zinger for you. It’s the weirdest coincidence in Physics. Are you ready?” <cheers from the physicists in the crowd> “Suppose all alone in the Universe there’s a rock and a planet and the rock is falling straight in towards the planet.” <turns to Al’s conveniently‑placed whiteboard> “We got two kinds of energy, right?”

Potential Energy    Kinetic Energy

Nods across the room except for Maybe-an-Art-major and a couple of Jeremy’s groupies. “Right. Potential energy is what you get from just being where you are with things pulling on you like the planet’s gravity pulls on the rock. Kinetic energy is what potential turns into when the pulls start you moving. For you Physics smarties, I’m gonna ignore temperature and magnetism and maybe the rock’s radioactive and like that, awright? So anyway, we know how to calculate each one of these here.”

PE = GMm/R    KE = ½mv²

“Big‑G is Newton’s gravitational constant, big‑M is the planet’s mass, little‑m is the rock’s mass, big‑R is how far apart the things are, and little‑v is how fast the rock’s going. They’re all just numbers and we’re not doing any complicated calculus or relativity stuff, OK? OK, to start with the rock is way far away so big‑R is huge. Big number on the bottom makes PE’s fraction tiny and we can call it zero. At the same time, the rock’s barely moving so little‑v and KE are both zero, close enough. Everybody with me?”

More nods, though a few of the physics students are looking impatient.

“Right, so time passes and the rock dives faster toward the planet Little‑v and kinetic energy get bigger. Where’s the energy coming from? Gotta be potential energy. But big‑R on the bottom gets smaller so the potential energy number gets, wait, bigger. That’s OK because that’s how much potential energy has been converted. What I’m gonna do is write the conversion as an equation.

GMm/R = ½mv²

“So if I tell you how far the rock is from the planet, you can work the equation to tell me how fast it’s going and vice-versa. Lemme show those straight out…”

v = √(2GM/R)    R = 2GM/v²

Some physicist hollers out. “The first one’s escape velocity.”

“Good eye. The energetics are the same going up or coming down, just in the opposite direction. One thing, there’s no little‑m in there, right? The rock could be Jupiter or a photon, same equations apply. Suppose you’re standing on the planet and fire the rock upward. If you give it enough little‑v speed energy to get past potential energy equals zero, then the rock escapes the planet and big‑R can be whatever it feels like. Big‑R and little‑v trade off. Is there a limit?”

A couple of physicists and an astronomy student see where this is going and start to grin.

“Newton physics doesn’t have a speed limit, right? They knew about the speed of light back then but it was just a number, you could go as fast as you wanted to. How about we ask how far the rock is from the planet when it’s going at the speed of light?”

R = 2GM/c²

Suddenly Jeremy pipes up. “Hey that’s the Event Horizon radius. I had that in my black hole term paper.” His groupies go “Oooo.”

“There you go, Jeremy. The same equation for two different objects, from two different theories of gravity, by two different derivations.”

“But it’s not valid for lightspeed.”

“How so?”

“You divided both sides of your conversion equation by little‑m. Photons have zero mass. You can’t divide by zero.”

Everyone in the room goes “Oooo.”

~~ Rich Olcott

A Diamond in The Sky with Lucy

On By rolcottIn Astronomy: Planetary Science, Space Travel, UncategorizedLeave a comment

Mid-afternoon coffee-and-scone time. As I step into his coffee shop Al’s quizzing Cathleen about something in one of his Astronomy magazines. “This Lucy space mission they just sent up, how come it looks like they’re shooting at either side of Jupiter instead of hitting it straight-on? And it’s got this crazy butterfly orbit that crosses the whole Solar System a couple of times. What sense does that make?”

Planned path of Lucy‘s mission to study Trojan asteroids (black dots).
After diagrams by NASA and Southwest Research Institute

“It shoots to either side because there’s interesting stuff out there. We think the Solar System started as a whirling disk of dust that gradually clumped together. The gravity from Jupiter’s clump scarfed up the lion’s share of the leftovers after the Sun coalesced. The good news is, not all of Jupiter’s hoard wound up in the planet. Some pieces made it to Jupiter’s orbit but then collected in the Trojan regions ahead and behind it. Looking at that material may teach us about the early Solar System.”

“Way out there? Why not just fall into Jupiter like everything else did?”

I do Physics, I can’t help but cut in. “It’s the many‑body problem in its simplest case, just the Sun, Jupiter and an asteroid in a three‑body interaction—”

Cathleen gives me a look. “Inappropriate physicsplaining, Sy, we’re talking Astronomy here. Al’s magazine is about locating and identifying objects in space. These asteroids happen to cluster in special locations roughly sixty degrees away from Jupiter.”

“But Al’s question was, ‘Why?‘ You told him why we’re sending Lucy to the Trojans, but Physics is why they exist and why that mission map looks so weird.”

“Good point, go ahead. OK with you, Al?”

“Sure.”

I unholster Old Reliable, my tricked‑out tablet, and start sketching on its screen. “OK, orange dot’s Jupiter, yellow dot’s the Sun. Calculating their motion is a two-body problem. Gravity pulls them together but centrifugal force pulls them apart. The forces balance when the two bodies orbit in ellipses around their common center of gravity. Jupiter’s ellipse is nearly a circle but it wobbles because the Sun orbits their center of gravity. Naturally, once Newton solved that problem people turned to the next harder one.”

“That’s where Lucy comes in?”

“Not yet, Al, we’ve still got those Trojan asteroids to account for. Suppose the Jupiter‑Sun system’s gravity captures an asteroid flying in from somewhere. Where will it settle down? Most places, one body dominates the gravitational field so the asteroid orbits that one. But suppose the asteroid finds a point where the two fields are equal.”

“Oh, like halfway between, right?”

“Between, Al, but not halfway.”

“Right, Cathleen. The Sun/Jupiter mass ratio and Newton’s inverse‑square law put the equal‑pull point a lot closer to Jupiter than to the Sun. If the asteroid found that point it would hang around forever or until it got nudged away. That’s Lagrange’s L1 point. There are two other balance points along the Sun‑Jupiter line. L2 is beyond Jupiter where the Sun’s gravity is even weaker. L3 is way on the other side of the Sun, a bit inside Jupiter’s orbit.”

“Hey, so those 60° points on the orbit, those are two more balances because they’re each the same distance from Jupiter and the Sun, right?”

“There you go, Al. L4 leads Jupiter and L5 runs behind. Lagrange published his 5‑point solution to the three‑body problem in 1762, just 250 years ago. The asteroids found Jupiter’s Trojan regions billions of years earlier.”

“We astronomers call the L4 cluster the Trojan camp and the L5 cluster the Greek camp, but that’s always bothered me. It’d be OK if we called the planet Zeus, but Jupiter’s a Roman god. Roman times were a millennium after classical Greece’s Trojan War so the names are just wrong.”

“I hadn’t thought about that, Cathleen, but you’re right. Anyway, back to Al’s diagram of Lucy’s journey. <activating Old Reliable’s ‘Animate’ function> Sorry, Al, but you’ve been misled. The magazine’s butterfly chart has Jupiter standing still. Here’s a stars-eye view. It’s more like the Trojans will come to Lucy than the reverse.”

~~ Rich Olcott

The Gelato Model

On By rolcottIn Cosmology, Mathematics, Physics: Newton and Gravity, UncategorizedLeave a comment

“Eddie, this ginger gelato’s delicious — not too sweet and just the right amount of ginger bite.”

“Glad you like it, Anne.”

“On the way down here, Sy was telling me about how so many things in the Universe run on the same mathematics if you look at them with the right coordinate system. Sy, how do you pick ‘the right coordinate system?”

“The same way you pick the right property to serve as a momentum in Newton’s Equation of Motion — physical intuition. You look for things that fit the system. Sometimes that puts you on the road to understanding, sometimes not. Eddie, you keep track of your gelato sales by flavor. How are they doing?”

“Pistachio’s always a good seller, Sy, but ginger has been coming on strong this year.”

“In motion terns, pistachio’s momentum is constant but ginger is gaining momentum, right?”

“S’what I said.”

“Measured in dollars or trayfuls?”

“In batches. I make it all in-house. I’m proud of that. Dollars, too, of course, but that’s just total for all flavors.”

“Batches all the same size?”

“Some are, some not, depending. If I had a bigger machine I could make more but I do what I can.”

“There you go, Anne, each gelato flavor is like a separate degree of freedom. Eddie’s tracked sales since he started so we can take that date as the origin. Measuring change along any degree in either batches or dollars we have perfectly respectable coordinates although the money view of the system is fuzzier. Velocity is batches per unit time, there’s even a speed limit, and ginger has accelerated. Sound familiar?”

“Sounds like you’re setting up a Physics model.”

“Call it gelato trend physics, but I don’t think I can push the analogy much further. The next step would be to define a useful momentum like Newton did with his Law of Motion.”

“F=ma? That’s about acceleration, isn’t it?”

“Probably not in Newton’s mind. Back in his day they were arguing about which was conserved, energy or momentum. It was a sloppy argument because no‑one agreed on crisp definitions. People could use words like ‘quantity of motion‘ to refer to energy or momentum or even something else. Finally Newton defined momentum as ‘mass times velocity‘, but first he had to define ‘mass‘ as ‘quantity of matter‘ to distinguish it from weight which he showed is a force that’s indirectly related to mass.”

“So is it energy or momentum that’s conserved?”

“Both, once you’ve got good definitions of them. But my point is, our car culture has trained us to emphasize acceleration. Newton’s thinking centered on momentum and its changes. In modern terms he defined force as momentum change per unit time. I’m trying to think of a force‑momentum pair for Eddie’s gelato. That’s a problem because I can’t identify an analog for inertia.”

“Inertia? What’s that got to do with my gelato?”

“Not much, and that’s the problem. Inertia is resistance to force. Who can resist gelato? If it weren’t for inertia, the smallest touch would be enough to send an object at high speed off to forever. The Universe would be filled with dust because stars and planets would never get the chance to form. But here we are, which I consider a good thing. Where does inertia come from? Newton changed his mind a couple of times. To this day we only have maybe‑answers to that question.”

“You know we want to know, Sy.”

“Einstein’s favorite guess was Mach’s Principle. There’s about a dozen different versions of the basic idea but they boil down to matter interacting with the combined gravitational and electromagnetic fields generated by the entire rest of the Universe.”

“Wow. Wait, the stars are far away and the galaxies are much, much further away. Their fields would be so faint, how can they have any effect at all?”

“You’re right, Anne, field intensity per star does drop with distance squared. But the number of stars goes up with distance cubed. The two trends multiply together so the force trends grow linearly. It’s a big Universe and size matters.”

“So what about my gelato?”

“We’ll need more research, Eddie. Another scoop of ginger, Anne?”

~~ Rich Olcott