Category: Physics

Zoning Out over Jupiter

On By rolcottIn Astronomy: Planetary Science, Mathematics: Spherical Harmonics, Physics: Waves, UncategorizedLeave a comment

I’m nursing my usual mug of eye‑opener in Cal’s Coffee Shop when astronomer Cathleen and chemist Susan chatter in. “Morning, ladies. Cathleen, prepare to be even more smug.”

“Ooo, what should I be smug about?”

“Your Jupiter suggestion. Grab some coffee and a couple of chairs.” <screen‑tapping on Old Reliable> “Ready? First step — purple and violet. You’ll never see violet or purple light coming from a standard video screen.”

“He’s going spectrum‑y on us, right, Cathleen?”

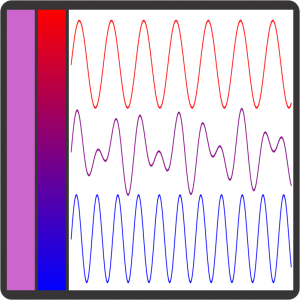
“More like anti‑spectrum‑y, Susan. Purple light doesn’t exist in the spectrum. We only perceive that color when we see red mixed with blue like that second band on Sy’s display. Violet light is a thing in nature, we can see it in flowers and dyes and rainbows beyond blue. Standard screens can’t show violet because their LEDs just emit red, blue and green wavelengths. Old Reliable uses mixtures of those three to fake all its colors. Where are you going with this, Sy?””

“Deeper into Physics. Cast your eyes upon the squiggles to the right. The one in the middle represents the lightwave coming from purple‑in‑the‑middle. The waveform’s jaggedy, but if you compare peaks and troughs you can see its shape is the sum of the red and blue shapes. I scaled the graphs up from 700 nanometers for red and 450 for blue.”

“Straightforward spectroscopy, Sy, Fourier analysis of a complicated linear waveform. Some astronomers make their living using that principle. So do audio engineers and lots of other people.”

“Patience, Cathleen, I’m going beyond linear. Fourier’s work applies to variation along a line. Legendre and Poisson extended the analysis to—”

“Aah, spherical harmonics! I remember them from Physical Chemistry class. They’re what gives shapes to atoms. They’ve got electron shells arranged around the nucleus. Electron charge stays as close to the nucleus as quantum will let it. Atoms absorb light energy by moving charge away from there. If the atom’s in a magnetic field or near other atoms that gives it a z-axis direction then the shells split into wavey lumps going to the poles and different directions and that’s your p-, d– and f-orbitals. Bigger shells have more room and they make weird forms but only the transition metals care about that.”

The angular portion of the lowest-energy spherical harmonics
Credit: Inigo.quilez, under CCA SA 3.0 license
Adapted from Wieczorek and Meschede under CC BY-NC-ND 4.0

“Considering you left out all the math, Susan, that’s a reasonable summary. I prefer to think of spherical harmonics as combinations of wave shapes at right angles. Imagine a spherical blob of water floating in space. If you tap it on top, waves ripple down to the bottom and back up again and maybe back down again. Those are zonal waves. A zonal harmonic averages over all E‑W longitudes at each N‑S latitude. Or you could stroke the blob on the side and set up a sectorial wave pattern that averages latitudes.”

“How about center‑out radial waves?”

“Susan’s shells do that job. My point was going to be that what sine waves do for characterizing linear things like sound and light, spherical harmonics do for central‑force systems. We describe charge in atoms, yes, but also sound coming from an explosion, heat circulating in a star, gravity shaping a planet. Specifically, Jupiter. Kaspi’s paper you gave me, Cathleen, I read it all the way to the Results table at the tail end. That was the rabbit‑hole.”

“Oh? What’s in the table?”

“Jupiter’s zonal harmonics — J‑names in the first column, J‑intensities in the second. Jn‘s shape resembles a sine wave and has n zeroes. Jupiter’s never‑zero central field is J0. Jn increases or decreases J0‘s strength wherever it’s non‑zero. For Jupiter that’s mostly by parts per million. What’s cool is the pattern you see when you total the dominating Jeven contributions.”

Data from Kaspi, et al.

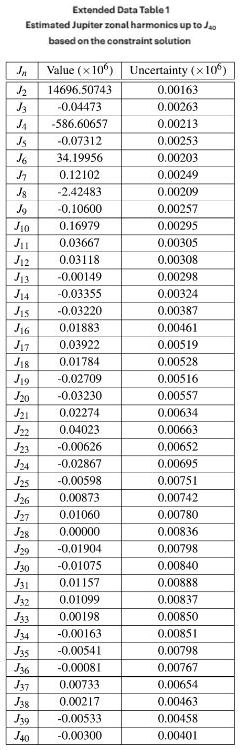
Cathleen’s squinting in thought. “Hmm… green zone A would be excess gravity from Jupiter’s equatorial bulge. B‘s excess is right where Kaspi proposed the heavy downflow. Ah‑HAH! C‘s pink deficit zone’s right on top of the Great Red Spot’s buoyant updraft. Perfect! Okay, I’m smug.”

~ Rich Olcott

Not Silly-Season Stuff, Maybe

On By rolcottIn Chemistry, Physics: Electromagnetism, UncategorizedLeave a comment

“Keep up the pace, Mr Feder, air conditioning is just up ahead.”

“Gotta stop to breathe, Moire, but I got just one more question.”

“A brief pause, then. What’s your question?”

“What’s all this about LK99 being a superconductor? Except it ain’t? Except maybe it is? What is LK99, anyway, and how do superconductors work? <puffing>”

“So many question marks for just one question. Are you done?”

“And why do news editors care?”

“There’s lots of ways we’d put superconductivity to work if it didn’t need liquid‑helium temperatures. Efficient electric power transmission, portable MRI machines, maglev trains, all kinds of advances, maybe even Star Trek tricorders.”

“Okay, I get how zero‑resistance superconductive wires would be great for power transmission, but how do all those other things have anything to do with it?”

“They depend on superconductivity’s conjoined twin, diamagnetism.”

“Dia—?”

“Means ‘against.’ It’s sort of an application of Newton’s Third Law.”

“That’s the one says, ‘If you push on the Universe it pushes back,’ right?”

“Very good, Mr Feder. In electromagnetism that’s called Lenz’ Law. Suppose you bring a magnet towards some active conductor, say a moving sheet of copper. Or maybe it’s already carrying an electric current. Either way, the magnet’s field makes charge carriers in the sheet move perpendicular to the field and to the prevailing motion. That’s an eddy current.”

“How come?”

“Because quantum and I’m not about to get into that in this heat. Emil Lenz didn’t propose a mechanism when he discovered his Law in 1834 but it works. What’s interesting is what happens next. The eddy current generates its own magnetic field that opposes your magnet’s field. There’s your push‑back and it’s called diamagnetism.”

“I see where you’re going, Moire. With a superconductor there’s zero resistance and those eddy currents get big, right?”

“In theory they could be infinite. In practice they’re exactly strong enough to cancel out any external magnetic field, up to a limit that depends on the material. A maglev train’s superconducting pads would float above its superconducting track until someone loads it too heavily.”

“What about portable MRI you said? It’s not like someone’s gonna stand on one.”

“A portable MRI would require a really strong magnet that doesn’t need plugging in. Take that superconducting sheet and bend it into a doughnut. Run your magnet through the hole a few times to start a current. That current will run forever and so will the magnetic field it generates, no additional power required. You can make the field as strong as you like, again within a limit that depends on the material.”

“Speaking of materials, what’s the limit for that LK99 stuff?”

“Ah, just in time! Ahoy, Susan! Out for a walk yourself, I see. We’re on our way to Al’s for coffee and air conditioning. Mr Feder’s got a question that’s more up your Chemistry alley than my Physics.”

“LK99, right? It’s so newsy.”

“Yeah. What is it? Does it superconduct or not?”

“Those answers have been changing by the week. Chemically, it’s basically lead phosphate but with copper ions replacing some of the lead ions.”

“They can do that?”

“Oh yes, but not as neatly as we’d like. Structurally, LK99’s an oxide framework in the apatite class — a lattice of oxygens with phosphorus ions sitting in most of the holes in the lattice, lead ions in some of the others. Natural apatite minerals also have a sprinkling of hydroxides, fluorides or chlorides, but the reported synthesis doesn’t include a source for any of those.”

“Synthesis — so the stuff is hand‑made?”

“Mm‑hm, from a series of sold‑state reactions. Those can be tricky — you grind each of your reactants to a fine powder, mix the powders, seal them in a tube and bake at high temperature for hours. The heat scrambles the lattices. The atoms can settle wherever they want, mostly. I think that’s part of the problem.”

“Like maybe they don’t?”

“Maybe. There are uncontrollable variables — grinding precision, grain size distribution, mixing details, reaction tube material, undetected but critical impurities — so many. That’s probably why other labs haven’t been able to duplicate the results. Superconductivity might be so structure‑sensitive that you have to prepare your sample j‑u‑s‑t right.”

~~ Rich Olcott

Little Strings And Big Ones

On By rolcottIn Cosmology, Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

It’ll be another hot day so I’m walking the park early. No geese in the lake — they’ve either flown north or else they’re attacking a farmer’s alfalfa field. A familiar voice shatters the quiet. “Wait up, Moire, I got questions.”

“Good morning, Mr Feder. First question, but please pick up your pace, I want to get back to the air conditioning.”

“I thought string theory was about little teeny stuff but this guy said about cosmic strings. How can they be teeny and cosmic?”

“They can’t. Totally different things, probably. Next question.”

“C’mon, Moire, that wasn’t even an answer, just opened up a bunch more questions.”

“It’s a tangled path but the track mostly started in the late 18th Century. Joseph Fourier derived the equation for how heat progresses along a uniform metal bar. Turned out the equation’s general solution was the sum of an infinite series of sine waves.”

“Sign waves? Like a protest rally?”

“Haha. No, s‑i‑n‑e, a mathematical function where something regularly and smoothly deviates about some central value. Anyhow, mathematicians soon realized that Fourier’s cute trick for his heat equation could be applied to equations for everything from sound waves to signal processing to pretty much all of Physics. Economics, even. Any time you use the word ‘frequency‘ you owe something to Fourier.”

“If he ain’t got it in writing from the Patent Office, I ain’t paying nothing.”

“It’s not the kind of thing you can patent, and besides, he lived in France and died almost two centuries ago. Be generous with your gratitude, at least. Let’s move on. Fourier’s Big Idea was already <ahem> in the air early in the 20th Century when Bohr and the Physics gang were looking at atoms. No surprise, they extended the notion to describe how electronic charge worked in there.”

“I’m waiting for the strings.”

“The key is that an atom’s a confined system like a guitar string that only vibrates between the bridge and whatever fret you’re pressing on. Sound waves traveling in open space can have any wavelength, but if you pluck a confined guitar string the only wavelengths you can excite are whole number multiples of its active length. No funny fractions like π/73 of the length no matter how hard or soft you pluck the string. Atoms work the same way — charge is confined around the nucleus so only certain wave sizes and shapes are allowed.”

“You said ‘strings.’ We getting somewhere finally?”

“Closing in on it. String theory strings aren’t just teeny. If your body were suddenly made as large as the Observable Universe, string theory is about what might happen inside a box a billion times smaller than your size now.”

“Really tight quarters, got it, so only certain vibrations are allowed.”

“Mm-hm, except it’s not really vibration, it would be something that acts mathematically like vibration. Go back to your guitar string. Plucking gives it up‑down motion, strumming moves it side‑to‑side. Two degrees of freedom. The math says whatever’s going on in a string theory box needs 8 or 11 or maybe 25 degrees of freedom, depending on the theory. At the box‑size scale if there’s structure at all it looks nothing like a string.”

“Then how about the big cosmic strings? What’s confining them?”

“Nothing, and I mean that literally. If they exist they’re bounded by different flavors of empty space. It goes back to what we think happened right after the Big Bang during rapid space expansion. Whatever forces drove the process were probably limited by lightspeed. Local acceleration in one region wouldn’t immediately affect events in regions lightyears away. Nearly adjacent parts of the Universe could have been evolving at very different rates. Have you ever watched the whirlpools that form when a fast‑moving stream of water meets a slower‑moving one?”

“Fort Lee had a storm‑sewer pipe that let into the Hudson River. You got crazy whirlpools there after a hard rain.”

“Whirlpools are one kind of topological defect. They die away in water because friction dissipates the angular momentum. Hiding behind a whole stack of ifs and maybes, some theorists think collisions between differently‑evolving spacetime structures might generate long‑lived defects like cosmic strings or sheets.”

~~ Rich Olcott

LIGO And NANOGrav

On By rolcottIn Astronomy: Techniques, Gravitational astronomy, Physics: Waves, UncategorizedLeave a comment

Afternoon coffee time, but Al’s place is a little noisier than usual. “Hey, Sy, come here and settle this.”

“Settle what, Al? Hi, Vinnie.”

<waves magazine> “This NANOGrav thing, they claim it’s a brand‑new kind of gravity wave. What’s that about?”

“Does it really say, ‘gravity wave‘? Let me see that. … <sigh> Press release journalism at its finest. ‘Gravity waves’ and ‘gravitational waves’ are two entirely different things.”

“I kinda remember you wrote about that, but it was so long ago I forget how they’re different.”

“Gravity waves happen in a fluid, like air or the ocean. Some disturbance, like a heat spike or an underwater landslide, pushes part of the fluid upward relative to a center of gravity. Gravity acts to pull that part down again but in the meantime the fluid’s own internal forces spread the initial up‑shift outwards. Adjacent fluid segments pull each other up and down and that’s a gravity wave. The whole process keeps going until friction dissipates the energy.”

“Gravitational waves don’t do that?”

“No, because gravitational waves temporarily modify the shape of space itself. The center doesn’t go up and down, it…” <showing a file on Old Reliable> “Here, see for yourself what happens. It’s called quadrupolar distortion. Mind you, the effects are tiny percentagewise which is why the LIGO apparatus had to be built kilometer‑scale in order to measure sub‑femtometer variations. The LIGO engineers took serious precautions to prevent gravity waves from masquerading as gravitational waves.”

“Alright, so now we’ve almost got used to LIGO machines catching these waves from colliding black holes and such. How are NANOGrav waves different?”

“Is infrared light different from visible light?”

“The Hubble sees visible but the Webb sees infrared.”

“Figures you’d have that cold, Al. What I think Sy’s getting at is they’re both electromagnetic even though we only see one of them. You’re gonna say the same for these new gravitational waves, right, Sy?”

“Got it in one, Vinnie. There’s only one electromagnetic field in the Universe but lots of waves running through it. Visible light is about moving charge between energy levels in atoms or molecules which is how the visual proteins in our eyes pick it up. Infrared can’t excite electrons. It can only waggle molecule parts which is why we feel it as heat. Same way, there’s only one gravitational field but lots of waves running through it. The LIGO devices are tuned to pick up drastic changes like the <ahem> massive energy release from a black hole collision.”

“You said ‘tuned‘. Gravitational waves got frequencies?”

“Sure. And just like light, high frequencies reflect high‑energy processes. LIGO detects waves in the kilohertz range, thousands of peaks per second. NANOGrav’s detection range is sub‑nanohertz, where one cycle can take years to complete. Amazingly low energy.”

“How can they detect anything that slow?”

“With really good clocks and a great deal of patience. The new reports are based on fifteen years of data, half a billion seconds counted out in nanoseconds.”

“Hey, wait a minute. LIGO’s only half‑a‑dozen years old. Where’d they get the extra data from, the future?”

“Of course not. Do you remember us working out how LIGO works? The center sends out a laser pulse along two perpendicular arms, then compares the two travel times when the pulse is reflected back. Light’s distance‑per‑time is constant, right? When a passing gravitational wave squeezes space along one arm, the pulse in that arm completes its round trip faster. The two times don’t match any more and everyone gets excited.”

“Sounds familiar.”

“Good. NANOGrav also uses a timing‑based strategy, but it depends on pulsars instead of lasers. Before you ask, a pulsar is a rotating neutron star that blasts a beam of electromagnetic radiation. What makes it a pulsar is that the beam points away from the rotation axis. We only catch a pulse when the beam points straight at us like a lighthouse or airport beacon. Radio and X‑ray observatories have been watching these beasts for half a century but it’s only in the past 15 years that our clocks have gotten good enough to register timing hiccups when a gravitational wave passes between us and a pulsar.”

~ Rich Olcott

SPLASH Splish plink

On By rolcottIn Astronomy: Stellar Science, Physics: Black Holes and Relativity, UncategorizedLeave a comment

<chirp, chirp, chirp, chirp> “Moire here. This’d better be good.”

“Hello, Mr Moire. I’m one of your readers.”

“Do you have any idea what time it is?”

“Afraid not, I don’t know what time zone you’re in.”

“It’s three o’clock in the morning! Why are you calling me at this hour?”

“Oh, sorry, it’s mid-afternoon here. Modern communications tech is such a marvel. No matter, you’re awake so here’s my question. I’ve been pondering that micro black hole you’ve featured in the last couple of posts. You convinced me it would have a hard time hitting Earth but then I started thinking about it hitting the Sun. The Sun’s diameter is 100 times Earth’s so it presents 10,000 times more target area, yes? Further, the Sun’s 300,000 times more massive than Earth so it has that much more gravity. Surely the Sun is a more effective black hole attractor than Earth is.”

“That’s a statement, not a question. Worse yet, you’re comparing negligible to extremely negligible and neither one is worth losing sleep over which is what I’m doing now.”

“Wait on, I’ve not gotten to my question yet which is, suppose a black hole did happen to collide with the Sun. What would happen then?”

<yawn> “Depends on the size of the black hole. If it’s supermassive, up in the billion‑sun range, it wouldn’t hit the Sun. Instead, the Sun would hit the black hole but there’d be no collision. The Sun would just sink quietly through the Event Horizon.”

“Wouldn’t it rip apart?”

“You’re thinking of those artistic paintings showing great blobs of material being torn away by a black hole’s gravity. Doesn’t work that way, at least not at this size range.” <grabbing Old Reliable from my nightstand and key‑tapping> “Gravitational forces are distance‑dependent. Supermassives are large even by astronomical standards. The M87* black hole, the first one ESA got an image of, has the mass of 6 billion Suns and an Event Horizon three times wider than Pluto’s orbit. The tidal ripping‑apart you’re looking for only happens when the mass centers of two objects approach within Roche’s limit. Suppose a Sun‑sized star flew into M87*’s Event Horizon. Their Roche limit would be 100 astronomical units inside the Event Horizon. If any ripping happened, no evidence could escape to us.”

“Another illusion punctured.”

“Don’t give up hope. The next‑smaller size category have masses near our Sun’s. The Event Horizon of a 10‑solar‑mass black hole would be only about 60 kilometers wide. The Roche Zone for an approaching Sun is a million times wider. There’s plenty of opportunity for ferocious ripping on the way in.”

“Somehow that’s a comfort, but my question was about even smaller black holes — micro‑size flyspecks such as you wrote about. What effect would one have on the Sun?”

“You’d think it’d be a simple matter of the micro‑hole, let’s call it Mikey, diving straight to the Sun’s center while gobbling Sun‑stuff in a gluttonous frenzy, getting exponentially bigger and more voracious every second until the Sun implodes. Almost none of that would happen. The Sun’s an incredibly violent place. On initial approach Mikey’d be met with powerful, rapidly moving magnetic fields. If he’s carrying any charge at all they’d give him whip‑crack rides all around the Sun’s mostly‑vacuum outer layers. He might not ever escape down to the Convection Zone.”

“He’d dive if he escaped there or he’s electrically neutral.”

“Mostly not. The Convection Zone’s 200,000-kilometer depth takes up two‑thirds of the Sun’s volume and features hyper‑hurricane winds roaring upward, downward and occasionally sideward. Mikey would be a very small boat in a very big forever storm.”

“But surely Mikey’s density would carry him through to the core.”

“Nope, the deeper you go, the smaller the influence of gravity. Newton proved that inside a massive spherical shell, the net gravitational pull on any small object is zero. At the Sun’s core it’s all pressure, no gravity.”

“Then the pressure will force‑feed mass into Mikey.”

“Not so much. Mikey has jets and and an accretion disk. Their outward radiation pressure sets an upper limit on Mikey’s gobbling speed. The Sun will nova naturally before Mikey has any effect.”

“No worries then.”

~~ Rich Olcott

Hiding Among The Hill Spheres

On By rolcottIn Astronomy, Physics: Black Holes and Relativity, Space Travel, UncategorizedLeave a comment

Bright Spring sunlight wakes me earlier than I’d like. I get to the office before I need to, but there’s Jeremy waiting at the door. “Morning, Jeremy. What gets you here so soon after dawn?”

“Good morning, Mr Moire. I didn’t sleep well last night, still thinking about that micro black hole. Okay, I know now that terrorists or military or corporate types couldn’t bring it near Earth, but maybe it comes by itself. What if it’s one of those asteroids with a weird orbit that intersects Earth’s orbit? Could we even see it coming? Aren’t we still in danger of all those tides and quakes and maybe it’d hollow out the Earth? How would the planetary defense people handle it?”

“For so early in the day you’re in fine form, Jeremy. Let’s take your barrage one topic at a time, starting with the bad news. We know this particular object would radiate very weakly and in the far infrared, which is already a challenge to detect. It’s only two micrometers wide. If it were to cross the Moon’s orbit, its image then would be about a nanoarcsecond across. Our astrometers are proud to resolve two white‑light images a few milliarcseconds apart using a 30‑meter telescope. Resolution in the far‑IR would be about 200 times worse. So, we couldn’t see it at a useful distance. But the bad news gets worse.”

“How could it get worse?”

“Suppose we could detect the beast. What would we do about it? Planetary defense people have proposed lots of strategies against a marauding asteroid — catch it in a big net, pilot it away with rocket engines mounted on the surface, even blast it with A‑bombs or H‑bombs. Black holes aren’t solid so none of those would work. The DART mission tried using kinetic energy, whacking an asteroid’s moonlet to divert the moonlet‑asteroid system. It worked better than anyone expected it to, but only because the moonlet was a rubble pile that broke up easily. The material it threw away acted as reaction mass for a poorly controlled rubble rocket. Black holes don’t break up.”

“You’re not making getting to sleep any easier for me.”

“Understood. Here’s the good news — the odds of us encountering anything like that are gazillions‑to‑one against. Consider the probabilities. If your beast exists I don’t think it would be an asteroid or even from the Kuiper Belt. Something as exotic as a primordial black hole or a mostly‑evaporated stellar black hole couldn’t have been part of the Solar System’s initial dust cloud, therefore it wouldn’t have been gathered into the Solar System’s ecliptic plane. It could have been part of the Oort cloud debris or maybe even flown in on a hyperbolic orbit from far, far away like ‘Oumuamua did. Its orbit could be along any of an infinite number of orientations away from Earth’s orbit. But it gets better.”

“I’ll take all the improvement you can give me.”

“Its orbital period is probably thousands of years long or never.”

“What difference does that make?”

“You’ve got to be in the right place at the right time to collide. Earth is 4.5 billion years old. Something with a 100‑year orbit would have had millions of chances to pass through a spot we happen to occupy. An outsider like ‘Oumuamua would have only one. We can even figure odds on that. It’s like a horseshoe game where close enough is good enough. The object doesn’t have to hit Earth right off, it only has to pierce our Hill Sphere.”

“Hill Sphere?”

“A Hill Sphere is a mathematical abstract like an Event Horizon. Inside a planet’s Sphere any nearby object feels a greater attraction to the planet than to its star. Velocities permitting, a collision may ensue. The Sphere’s radius depends only on the average planet–star distance and the planet and star masses. Earth’s Hill Sphere radius is 1.5 million kilometers. Visualize Hill Spheres crowded all along Earth’s orbit. If the interloper traverses any Sphere other than the one we’re in, we survive. It has 1 chance out of 471 . Multiply 471 by 100 spheres sunward and an infinity outward. We’ve got a guaranteed win.”

“I’ll sleep better tonight.”

~~ Rich Olcott

A Tug at The Ol’ Gravity Strings

On By rolcottIn Physics: Black Holes and Relativity, Space Travel, UncategorizedLeave a comment

“Why, Jeremy, you’ve got such a stunned look on your face. What happened? Is there anything I can do to help?”

“Sorry, Mr Moire. I guess I’ve been thinking too much about this science fiction story I just read. Which gelato can I scoop for you?”

“Two dips of mint, in a cup. Eddie went heavy with the garlic on my pizza this evening. What got to you in the story?”

“The central plot device. Here’s your gelato. In the story, someone locates a rogue black hole hiding in the asteroid belt. Tiny, maybe a few thousandths of a millimeter across, but awful heavy. A military‑industrial combine uses a space tug to tow it to Earth orbit for some kind of energy source, but their magnetic grapple slips and the thing falls to Earth. Except it doesn’t just fall to Earth, it’s so small it falls into Earth and now it’s orbiting inside, eating away the core until everything crumbles in. I can’t stop thinking about that.”

“Sounds pretty bad, but it might help if we run the numbers.” <drawing Old Reliable from its holster> “First thing — Everything about a black hole depends on its mass, so just how massive is this one?” <tapping on Old Reliable’s screen with gelato spoon> “For round numbers let’s say its diameter is 0.002 millimeter. The Schwartzschild ‘radius’ r is half that. Solve Schwartschild’s r=2GM/c² equation for the mass … plug in that r‑value … mass is 6.7×1020 kilograms. That’s about 1% of the Moon’s mass. Heavy indeed. How did they find this object?”

“The story didn’t say. Probably some asteroid miner stumbled on it.”

“Darn lucky stumble, something only a few microns across. Not likely to transit the Sun or block light from any stars unless you’re right on top of it. Radiation from its accretion disk? Depends on the history — there’s a lot of open space in the asteroid belt but just maybe the beast encountered enough dust to form one. Probably not, though. Wait, how about Hawking radiation?”

“Oh, right, Stephen Hawking’s quantum magic trick that lets a black hole radiate light from just outside its Event Horizon. Does Old Reliable have the formulas for that?”

“Sure. From Hawking’s work we know the object’s temperature and that gives us its blackbody spectrum, then we’ve got the Bekenstein‑Hawking equation for the power it radiates. Mind you, the spectrum will be red‑shifted to some extent because those photons have to crawl out of a gravity well, but this’ll give us a first cut.” <more tapping> “Chilly. 170 kelvins, that’s 100⁰C below room temperature. Most of its sub‑nanowatt emission will be at far infrared wavelengths. A terrible beacon. But suppose someone did find this thing. I wonder what’ll it take to move it here.”

“Can you calculate that?”

“Roughly. Suppose your space tug follows the cheapest possible flight path from somewhere near Ceres. Assuming the tug itself has negligible mass … ” <more tapping> “Whoa! That is literally an astronomical amount of delta-V. Not anything a rocket could do. Never mind. But where were they planning to put the object? What level orbit?”

“Well, it’s intended to beam power down to Earth. Ions in the Van Allen Belts would soak up a lot of the energy unless they station it below the Belts. Say 250 miles up along with the ISS.”

“Hoo boy! A thousand times closer than the Moon. Force is inverse to distance squared, remember. Wait, that’s distance to the center and Earth’s radius is about 4000 miles so the 250 miles is on top of that. 250,000 divided by 4250 … quotient squared … is a distance factor of almost 3500. Put 1% of the Moon that close to the Earth and you’ve got ocean tides 36 times stronger than lunar tides. Land does tides, too, so there’d be earthquakes. Um. The ISS is on a 90‑minute orbit so you’d have those quakes and ocean tides sixteen times a day. I wouldn’t worry about the black hole hollowing out the Earth, the tidal effect alone would do a great job of messing us up.”

“The whole project is such a bad idea that no-one would or could do it. I feel better now.”

~~ Rich Olcott

Reflection, Rotation And Spacetime

On By rolcottIn Cosmology, Mathematics, Physics: Einstein, UncategorizedLeave a comment

“Afternoon, Al.”

“Hiya, Sy. Hey, which of these two scones d’ya like better?”

“”Mm … this oniony one, sorta. The other is too vegetable for me ‑ grass, I think, and maybe asparagus? What’s going on?”

“Experimenting, Sy, experimenting. I’m going for ‘Taste of Spring.’ The first one was spring onion, the second was fiddlehead ferns. I picked ’em myself.”

“Very seasonal, but I’m afraid neither goes well with coffee. I’ll take a caramel scone, please, plus a mug of my usual mud.”

“Aw, Sy, caramel’s a winter flavor. Here you go. Say, while you’re here, maybe you could clear up something for me?”

“I can try. What’s the something?”

“After your multiverse series I got out my astronomy magazines to read up on the Big Bang. Several of the articles said that we’ve gone through several … um, I think they said ‘epochs‘ … separated by episodes of symmetry breaking. What’s that all about?”

“It’s about a central notion in modern Physics. Name me some kinds of symmetry.”

“Mmm, there’s left‑right, of course, and the turning kind like a snowflake has. Come to think — I like listening to Bach and Vivaldi when I’m planet‑watching. I don’t know why but their stuff reminds me of geometry and feels like symmetry.”

“Would it help to know that the word comes from the Greek for ‘same measure‘? Symmetry is about transformations, like your mirror and rotation operations, that affect a system but don’t significantly change to its measurable properties. Rotate that snowflake 60° and it looks exactly the same. Both the geometric symmetries you named are two‑dimensional but the principle applies all over the place. Bach and the whole Baroque era were just saturated with symmetry. His music was so regular it even looked good on the page. Even buildings and artworks back then were planned to look balanced, as much mass and structure on the left as on the right.”

“I don’t read music, just listen to it. Why does Bach sound symmetric?”

“There’s another kind of symmetry, called a ‘translation‘ don’t ask why, where the transformation moves something along a line within some larger structure. That paper napkin dispenser, for instance. It’s got a stack of napkins that all look alike. I pull one off, napkins move up one unit but the stack doesn’t look any different.”

“Except I gotta refill it when it runs low, but I get your drift. You’re saying Bach takes a phrase and repeats it over and over and that sounds like translational symmetry along the music’s timeline.”

“Yup, maybe up or down a few tones, maybe a different register or instrument. The repeats are the thing. Play his Third Brandenberg Concerto next time you’re at your telescope, you’ll see what I mean.”

“Symmetry’s not just math then.”

“Like I said, it’s everywhere. You’ve seen diagrams of DNA’s spiral staircase. It combines translation with rotation symmetry, does about 10 translation steps per turn, over and over. The Universe has a symmetry you don’t see at all. No‑one did until Lorentz and Poincaré revised Heaviside’s version of Maxwell’s electromagnetism equations for Minkowski space. Einstein, Hilbert and Grossman used that work to give us and the Universe a new symmetry.”

“Einstein didn’t do the math?”

“The crew I just named were world‑class in math, he wasn’t. Einstein’s strengths were his physical intuition and his ability to pick problems his math buddies would find interesting. Look, Newton’s Universe depends on absolute space and time. The distance between two objects at a given time is always the same, no matter who’s measuring it or how fast anyone is moving. All observers measure the same duration between two incidents regardless. Follow me?”

“Makes sense. That’s how things work hereabouts, anyway.”

“That’s how they work everywhere until you get to high speeds or high gravity. Lorentz proved that the distances and durations you measure depend on your velocity relative to what you’re measuring. Extreme cases lead to inconsistent numbers. Newton’s absolute space and time are pliable. To Einstein such instability was an abomination. Physics needs a firm foundation, a symmetry between all observers to support consistent measurements throughout the Universe. Einstein’s Relativity Theory rescued Physics with symmetrical mathematical transformations that enforce consistency.”

~~ Rich Olcott

Noodles or A Sandwich?

On By rolcottIn Cosmology, Physics: Quantum Mechanics, UncategorizedLeave a comment

“Wait, Sy, your anti-Universe idea says there are exactly two um, sub‑Universes. Even the word ‘multiverse‘ suggests more than that.”

“You’re right, Susan, most of the multiverse proposals go to the other extreme. Maybe the most extreme version grew in reaction to one popular interpretation of quantum theory. Do you know about the ‘Many Worlds‘ notion?”

“Many Worlds? Is that the one about when I decide between noodles for lunch or a sandwich, the Universe splits and there’s one of me enjoying each one?”

“That’s the popular idea. The physics idea is way smaller, far bigger and even harder to swallow. Physicists have been arguing about it for a half‑century.”

“Come again? Smaller AND bigger?”

“Smaller because it’s a quantum‑based idea about microscopic phenomena. Doesn’t say anything about things big enough to touch. Remember how quantum calculations predict statistics, not exact values? They can’t give you anything but averages and spreads. Einstein and Bohr had a couple of marquee debates about that back in the 1930s. Bohr maintained that our only path to understanding observations at the micro‑scale was to accept that events there are random and there’s no point discussing anything deeper than statistics. Einstein’s position was that the very fact that we’re successfully using an average‑based strategy says that there must be finer‑grained phenomena to average over. He called it ‘the underlying reality.’ The string theory folks have chased that possibility all the way down to the Planck‑length scale. They’ve found lots of lovely math but not much else. Hugh Everett had a different concept.”

“With that build‑up, it’d better have something to do with Many Worlds.”

“Oh, it does. Pieces of the idea have been lying around for centuries, but Everett pulled them all together and dressed them up in a quantum suit. Put simply, in his PhD thesis he showed how QM’s statistics can result from averaging over Universes. Well, one Universe per observation, but you experience a sequence of Universes and that’s what you average over.”

“How can you show something like that?”

“By going down the rabbit hole step by step and staying strictly within the formal QM framework. First step was to abstractify the operation of observing. He said it’s a matter of two separate systems, an observer A and a subject B. The A could be a person or electronics or whatever. What’s important is that A has the ability to assess and record B‘s states and how they change. Given all that, the next step is to say that both A and B are quantized, in the sense that each has a quantum state.”

“Wait, EACH has a quantum state? Even if A is a human or a massive NMR machine?”

“That’s one of the hard‑to‑swallows, but formally speaking he’s okay. If a micro‑system can have a quantum state then so can a macro‑system made up of micro‑systems. You just multiply the micro‑states together to get the macro‑state. Which gets us to the next step — when A interrogates B, the two become entangled. We then can only talk about the combined quantum state of the A+B system. Everett referred to an Einstein quote when he wrote that a mouse doesn’t change the Moon by looking at it, but the Moon changes the mouse. The next step’s a doozy so take a deep breath.”

“Ready, I suppose.”

“B could have been in any of its quantum states, suppose it’s #10. After the observation, A+B must be an entangled mixture of whatever A was, combined with each of B‘s possible final states. Suppose B might switch to #42. Now we can have A+B(#42), separate from a persisting A+B(#10), plus many other possibles. As time goes by, A+B(#42) moves along its worldline independent of whatever happens to A+B(#10).”

“If they’re independent than each is in its own Universe. That’s the Many Worlds thing.”

“Now consider just how many worlds. We’re talking every potential observing macro‑system of any size, entangled with all possible quantum states of every existing micro‑system anywhere in our Observable Universe. We’re a long way from your noodles or sandwich decision.”

“An infinity of infinities.”

“Each in its own massive world.”

“Hard to swallow.”

~~ Rich Olcott

A Nightcap And Secrets

On By rolcottIn Computer science, Physics: Quantum Mechanics, UncategorizedLeave a comment

“A coffee nightcap, Sy? It’s decaf so Teena can have some.”

“Sounds good, Sis.”

“Why didn’t Mr Einstein like entanglement, Uncle Sy? Thanks, Mom. A little more cream in it, please.”

“I’ll bet it has to do with the instant-effect aspect, right, Sy?”

“Thanks, Sis, and you’re right as usual. All of Relativity theory rests on the claim that nothing, not light or gravity or causality itself, can travel faster than light in a vacuum. There’s good strong arguments and evidence to support that, but Einstein himself proved that entanglement effects aren’t constrained to lightspeed. Annoyed him no end.”

“Well, your coin story‘s very nice, but it’s just a story. Is there evidence for entanglement?”

“Oh, yes, though it was fifty years after Einstein’s entanglement paper before our technology got good enough to do the experiments. Since then a whole industry of academics and entrepreneurs has grown up to build and apply devices that generate entangled systems.”

“Systems?”

“Mm-hm. Most of the work has been done with pairs of photons, but people have entangled pairs of everything from swarms of ultra‑cold atoms to electrons trapped in small imperfect diamonds. It’s always a matter of linking the pair members through some shared binary property.”

“Binary! I know what that is. Brian has a computer toy he lets me play with. You tell it where to drive this little car and it asks for decisions like left‑right or go‑stop and they’re all yes or no and the screen shows your answer as ‘0’or ‘1’ and that’s binary, right?”

“Absolutely, Teena. The entangled thingies are always created in pairs, remember? Everything about each twin is identical except for that one property, like the two coin metals, so it’s yes, no, or some mixture. Cars can’t do mixtures because they’re too big for quantum.”

“What kinds of properties are we talking about? It’s not really gold and silver, is it?”

“No, you’re right about that, Sis. Transmutation takes way too much power. Entangled quantum states have little or no energy separation which is one reason the experiments are so hard. Photons are the easiest to work with so that’s where most of the entanglement work has been done. Typically the process splits a laser beam into two rays that have contrasting polarizations, say vertical and horizontal. Or the researchers might work with particles like electrons that you can split into right‑ and left‑handed spin. Whatever, call ’em ones and zeroes, you’ve got a bridge between quantum and computing.”

“Brian says binary can do secret codes.”

“He’s right about that. Codes are about hiding information. Entanglement is real good at hiding quantum information behind some strict rules. Rule one is, if you inspect an entangled particle, you break the entanglement.”

“Sounds reasonable. When you measure it you make it part of a big system and it’s not quantum any more.”

“Right, Sis. Rule two, an entanglement only links pairs. No triples or broadcasts. Rule three is for photons — you can have two independent ways to inspect a property, but you need to use the same way for both photons or you’ve got a 50% chance of getting a mismatch.”

“Oho! I see where the hiding comes in. Hmm… From what I’ve read, encryption’s big problem is guarding the key. I think those three rules make a good way to do that. Suppose Rocky and Bullwinkle want to protect their coded messages from Boris Badinoff. They share a series of entangled photon pairs. and they agree to a measurement protocol based on the published daily prices for a series of stocks — for each photon in a series, measure it with Method 1 if the corresponding price is an odd number, Method 2 if it’s even. Rocky measures his photon. If he measures a ‘1’ then Bullwinkle sees a ‘0’ for that photon and he knows Rocky saw a ‘1.’ Rocky encrypts his message using his measured bit string. Bullwinkle flips his bit string and decrypts.”

“Brilliant. Even if Boris knows the proper sequence of measurements, if he peeks at an entangled photon that breaks the entanglement. When Bullwinkle decodes gibberish Rocky has to build another key. Your Mom’s a very smart person, Teena.”

~ Rich Olcott