Tag: Symmetry

Symmetrical Eavesdropping

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

“Wait, Sy, you’ve made this explanation way more complicated than it has to be. All I asked about was the horrible whirling I’d gotten myself into. The three angular coordinates part would have done for that, but you dragged in degrees of freedom and deep symmetry and even dropped in that bit about ‘if measurable motion is defined.’ Why bother with all that and how can you have unmeasurable motion?”

“Curiosity caught the cat, didn’t it? Let’s head down to Eddie’s and I’ll treat you to a gelato. Your usual scoop of mint, of course, but I recommend combining it with a scoop of ginger to ease your queasy.”

“You’re a hard man to turn down, Sy. Lead on.”

<walking the hall to the elevators> “Have you ever baked a cake, Anne?”

“Hasn’t everyone? My specialty is Crazy Cake — flour, sugar, oil, vinegar, baking soda and a few other things but no eggs.”

“Sounds interesting. Well, consider the path from fixings to cake. You’ve collected the ingredients. Is it a cake yet?”

“Of course not.”

“Ok, you’ve stirred everything together and poured the batter into the pan. Is it a cake yet?”

“Actually, you sift the dry ingredients into the pan, then add the others separately, but I get your point. No, it’s not cake and it won’t be until it’s baked and I’ve topped it with my secret frosting. Some day, Sy, I’ll bake you one.”

<riding the elevator down to 2> “You’re a hard woman to turn down, Anne. I look forward to it. Anyhow, you see the essential difference between flour’s journey to cakehood and our elevator ride down to Eddie’s.”

“Mmm… OK, it’s the discrete versus continuous thing, isn’t it?”

“You’ve got it. Measuring progress along a discrete degree of freedom can be an iffy proposition.”

“How about just going with the recipe’s step number?”

“I’ll bet you use a spoon instead of a cup to get the right amount of baking soda. Is that a separate step from cup‑measuring the other dry ingredients? Sifting one batch or two? Those’d change the step‑number metric and the step-by-step equivalent of momentum. It’s not a trivial question, because Emmy Noether’s symmetry theorem applies only to continuous coordinates.”

“We’re back to her again? I thought—”

The elevator doors open at the second floor. We walk across to Eddie’s, where the tail‑end of the lunch crowd is dawdling over their pizzas. “Hiya folks. You’re a little late, I already shut my oven down.”

“Hi, Eddie, we’re just here for gelato. What’s your pleasure, Anne?”

“On Sy’s recommendation, Eddie, I’ll try a scoop of ginger along with my scoop of mint. Sy, about that symmetry theorem—”

“The same for me, Eddie.”

“Comin’ up. Just find a table, I’ll bring ’em over.”

We do that and he does that. “Here you go, folks, two gelati both the same, all symmetrical.”

“Eddie, you’ve been eavesdropping again!”

“Who, me? Never! Unless it’s somethin’ interesting. So symmetry ain’t just pretty like snowflakes? It’s got theorems?”

“Absolutely, Eddie. In many ways symmetry appears to be fundamental to how the Universe works. Or we think so, anyway. Here, Anne, have an extra bite of my ginger gelato. For one thing, Eddie, symmetry makes calculations a lot easier. If you know a particular system has the symmetry of a square, for instance, then you can get away with calculating only an eighth of it.”

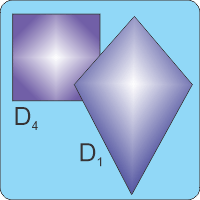
“You mean a quarter, right, you turn a square four ways.”

“No, eight. It’s done with mirrors. Sy showed me.”

“I’m sure he did, Anne. But Sy, what if it’s not a perfect square? How about if one corner’s pulled out to a kite shape?”

“That’s called a broken symmetry, no surprise. Physicists and engineers handle systems like that with a toolkit of approximations that the mathematicians don’t like. Basically, the idea is to start with some nice neat symmetrical solution then add adjustments, called perturbations, to tweak the solution to something closer to reality. If the kite shape’s not too far away from squareness the adjusted solution can give you some insight onto how the actual thing works.”

“How about if it’s too far?”

“You go looking for a kite‑shaped solution.”

~~ Rich Olcott

Deep Symmetry

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, UncategorizedLeave a comment

“Sy, I can understand mathematicians getting seriously into symmetry. They love patterns and I suppose they’ve even found patterns in the patterns.”

“They have, Anne. There’s a whole field called ‘Group Theory‘ devoted to classifying symmetries and then classifying the classifications. The split between discrete and continuous varieties is just the first step.”

“You say ‘symmetry‘ like it’s a thing rather than a quality.”

“Nice observation. In this context, it is. Something may be symmetrical, that’s a quality. Or it may be subject to a symmetry operation, say a reflection across its midline. Or it may be subject to a whole collection of operations that match the operations of some other object, say a square. In that case we say our object has the symmetry of a square. It turns out that there’s a limited number of discrete symmetries, few enough that they’ve been given names. Squares, for instance, have D4 symmetry. So do four-leaf clovers and the Washington Monument.”

“OK, the ‘4’ must be in there because you can turn it four times and each time it looks the same. What’s the ‘D‘ about?”

“Dihedral, two‑sided, like two appearances on either side of a reflection. That’s opposed to ‘C‘ which comes from ‘Cyclic’ like 1‑2‑3‑4‑1‑2‑3‑4. My lawn sprinkler has C4 symmetry, no mirrors, but add one mirror and bang! you’ve got eight mirrors and D4 symmetry.”

“Eight, not just four?”

“Eight. Two mirrors at 90° generate another one 45° between them. That’s the thing with symmetry operations, they combine and multiply. That’s also why there’s a limited number of symmetries. You think you’ve got a new one but when you work out all the relationships it turns out to be an old one looked at from a different angle. Cubes, for instance — who knew they have a three‑fold rotation axis along each body diagonal, but they do.”

“I guess symmetry can make physics calculations simpler because you only have to do one symmetric piece and then spread the results around. But other than that, why do the physicists care?”

“Actually they don’t care much about most of the discrete symmetries but they care a whole lot about the continuous kind. A century ago, a young German mathematician named Emmy Noether proved that within certain restrictions, every continuous symmetry comes along with a conserved quantity. That proof suddenly tied together a bunch of Physics specialties that had grown up separately — cosmology, relativity, thermodynamics, electromagnetism, optics, classical Newtonian mechanics, fluid mechanics, nuclear physics, even string theory—”

“Very large to very small, I get that, but how can one theory have that range? And what’s a conserved quantity?”

“It’s theorem, not theory, and it capped two centuries of theoretical development. Conserved quantities are properties that don’t change while a system evolves from one state to another. Newton’s First Law of Motion was about linear momentum as a conserved quantity. His Second Law, F=ma, connected force with momentum change, letting us understand how a straight‑line system evolves with time. F=ma was our first Equation of Motion. It was a short step from there to rotational motion where we found a second conserved quantity, angular momentum, and an Equation of Motion that had exactly the same form as Newton’s first one, once you converted from linear to angular coordinates.”

“Converting from x-y to radius-angle, I take it.”

“Exactly, Anne, with torque serving as F. That generalization was the first of many as physicists learned how to choose the right generalized coordinates for a given system and an appropriate property to serve as the momentum. The amazing thing was that so many phenomena follow very similar Equations of Motion — at a fundamental level, photons and galaxies obey the same mathematics. Different details but the same form, like a snowflake rotated by 60 degrees.”

“Ooo, lovely, a really deep symmetry!”

“Mm-hm, and that’s where Noether came in. She showed that for a large class of important systems, smooth continuous symmetry along some coordinate necessarily entails a conserved quantity. Space‑shift symmetry implies conservation of momentum, time‑shift symmetry implies conservation of energy, other symmetries lock in a collection of subatomic quantities.”

“Symmetry explains a lot, mm-hm.”

~~ Rich Olcott

Edged Things and Smooth Things

On By rolcottIn Cosmology, Mathematics, Physics: Fundamentals, Uncategorized2 Comments

“Yeughh, Sy, that whirling, the entire Universe spinning around me in every direction at once.”

“Well, you were at a point of spherical symmetry, Anne.”

“There’s that word ‘symmetry‘ again. Right side matches left side, what else is there to say?”

“A whole lot, especially after the mathematicians and physicists started playing with the basic notion.”

“Which is?”

“Being able to execute a transformation without making a relevant difference.”

“Relevant?”

“To the context. Swapping the king of spades for the king of hearts would be relevant in some card games but not others, right? If it doesn’t affect the play or the scoring, swapping those two when no‑one’s looking would be a legitimate symmetry operation. Spin a snowflake 60° and it looks the same unless you care exactly where each molecule is. That’s rotational symmetry, but there’s lots of geometric symmetry operations — reflections, inversions, glides, translations—”

“Translation is a symmetry operation?”

“In this connection, ‘translation‘ means movement or swapping between two different places in space. The idea came from crystals. Think of a 3D checkerboard, except the borderlines aren’t necessarily perpendicular. Perfect crystals are like that. Every cube‑ish cell contains essentially the same arrangement of atoms. In principle you could swap the contents of any two cells without making a difference in any of the crystal’s measurable properties. That’d be a translation symmetry operation.”

“Glides make me think of ice skating.”

“The glide operation makes me think of a chess knight’s move — a translation plus a reflection across the translation path. Think of wet footprints crossing a dry floor. That’s one example of combining operations to create additional symmetries. You can execute 48 unique symmetry operations on a cube even without the translation‑related ones. In my grad school’s crystallography class they taught us about point group and wallpaper and space group symmetries. It blew me away — beautiful in both mathematical and artistic senses. You’ve seen M C Escher’s art?”

“Of course, I love it. I pushed into his studio once to watch him work but he spotted me and shouted something Dutch at me. I’ve wondered what he thought when I pushed out of there.”

“His pieces drew heavily on geometric symmetries. So did Baroque art, music and architecture.”

“Music? Oh, yes — they had motifs and whole sections you could swap, and rhythm patterns and tunes you could read forwards and backwards like in a mirror… We’ve come a long way from snowflake symmetry, haven’t we?”

“We’re just getting started. Here’s where the Physics folks generalized the idea. Your unfortunate experience in space is right on the edge of what most people consider as symmetry. Were you impressed with the cube’s 48 operations?”

“I suppose. I haven’t had time to think about it.”

“A sphere has an infinite number. You could pick any of an infinite number of lines through its center. Each is an axis for an infinite number of rotational symmetries. Times two because there’s an inversion point at the center so the rotation could go in either direction. Then each line is embedded in an infinite number of reflection planes.”

“Goodness, no wonder I was dizzy. But it’s still geometry. What was the edge that the physicists went past?”

“The border between step‑at‑a‑time discrete symmetries and continuous ones. Rotate that snowflake 60° and you’ve got a match; anything not a multiple of 60° won’t pair things up. Across the border, some of the most important results in modern Physics depend on continuous symmetries.”

“How can you even have a continuous symmetry?”

“Here, I’ll draw a circle on this square of paper. I can rotate the square by 90, 180 or 270 degrees and everything’s just the way it was. But if the square’s not relevant because we’re only interested in the circle, then I can rotate the paper by any amount I like and it’s a no‑difference transformation, right?”

“Continuous like on an infinite line but it’s wrapped around.”

“Exactly, and your infinite line is another example — any translation along that line, by a mile or a millimeter, is a perfectly good symmetry operation.”

“Ooo, and time, too. I experience time as an infinite line.”

“So does everyone. but most only travel in one direction.”

~~ Rich Olcott

The Pizza Connection

On By rolcottIn Physics: Light and Relativity, Physics: Quantum Mechanics, UncategorizedLeave a comment

“Wait a minute, Sy. If Einstein’s logic proves we can’t have faster‑than‑light communication, what about all the entanglement hype I see in my science magazines?”

“Hype’s the right word, Vinnie. Entanglement’s a real effect, but it doesn’t play well as a communication channel.”

“OK, why not?”

“Let’s set the stage. We’re still in our personal spaceships and we’ve just ordered pizza from Eddie. The entanglement relationship is independent of time and distance so I’m going to skip over how fast we’re going and pretend that Eddie’s using transporter delivery technology, ok?”

“Fine with me,”

“Good. You order your usual double pepperoni with extra cheese, I ask for Italian sausage. Two pizza boxes suddenly appear on our respective mess tables. No reflection on Eddie, but suppose he has a history of getting orders crossed. The quantum formalism says because our orders were filled at the same time and in a single operation, the two boxes are entangled — we don’t know which is which. Before we open the boxes, each of us has a 50:50 shot of getting the right order. It’s like we’ve got a pair of Schrödinger pizzas, half one order and half the other until we look, right?”

“Won’t happen, Eddie’s a pro.”

“True, but stay with me here. I open my box and immediately I know which pizza you received, no matter how far away your ship is from mine. Is that instantaneous communication between us?”

“Of course not, I’m not gonna know which pizza either of us got until I open my own box. Then I’ll know what my meal’s gonna be and I’ll know what you’re having, too. Actually, I’m probably gonna know first because I get hungry sooner than you.”

“Good point. Anyway, entanglement doesn’t transmit human‑scale information. The only communication between us in our spaceships is still limited by Einstein’s rules. But this is a good setup for us to dig a little deeper into the quantum stuff. You rightly rejected the Schrödinger pizza idea because pizza’s human‑scale. One of those boxes definitely holds your pizza or else it definitely holds mine. There’s no in‑between mixtures with human‑scale pizzas. Suppose Eddie sent quantum‑scale nanopizzas, though. Now things get more interesting.”

“Eddie doesn’t mess up orders.”

<sigh> “Even Eddie can’t keep things straight if he sends out a pair of quantum‑scale pizzas. What’s inside a specific entangled box is called a local property. John Stewart Bell proved some statistical criteria for whether a quantum system’s properties are local or are somehow shared among the entangled objects. Scientists have applied his tests to everything from entangled photons up to little squares of diamond. They’ve tracked quantum properties from spin states to vibration modes. A lot of work went into plugging loopholes in Bell’s criteria.”

“What’d they find?”

“The results keep coming up non-local. Our quantum pizzas truly do not have separate characteristics hiding inside their boxes unless Eddie marked a box to destroy the symmetry. All the objects in an entanglement share all the applicable quantum property values until one object gets measured. Instantly, all the entangled objects snap into specific individual property values, like which box holds which pizza. They stop being entangled, too. That happens no matter how far apart they are. Those experimental results absolutely rule out the local‑property idea which was the most appealing version of the ‘underlying reality‘ that Einstein and Bohr argued over.”

“Wait, I can’t tell you anything faster than light, but these quantum thingies automatically do that instant‑like?”

“Annoying, isn’t it? But it’s a sparse form of messaging. My quantum pizza box can tell yours only two things, ‘I’ve been opened‘ and ‘I hold Italian sausage pizza.’ They’re one‑time messages at the quantum level and you as an observer can’t hear either one. Quantum theoreticians call the interaction ‘wave function collapse‘ but Einstein called it ‘spooky action at a distance.’ He hated even that limited amount of instantaneous communication because it goes directly against the first principle of Special Relativity. Relativity has been vigorously tested for over a century. It’s stood up to everything they’ve thrown at it — except for this little mouse nibbling at its base.”

~~ Rich Olcott

Big Bang│Gnab Gib?

On By rolcottIn Cosmology, UncategorizedLeave a comment

Anne’s an experienced adventurer, but almost exploding the Earth when she tried transporting herself into an anti‑Universe was a jolt. It takes her a while to calm down. Fortunately, I’m there to help. <long soothing pause> “Sy, I promise that’s one direction I’ll never ‘push’ to go again.”

“No reason to go there and big reasons not to. <long friendly pause> Hmm. You’ve told me that when you use your superpower to go somewhere, you can feel whether there’d be a wall or something in the way. That’s how you know to get to a safer location before you ‘push.’ Didn’t you get that feeling before you went to meet anti‑Anne?”

“No, it felt just like just any other ‘push.’ Why?”

“I’m curious. Could you feel for just a second in the direction opposite to anti‑Anne? For Heaven sake don’t go there! Just look, OK?”

“All right … <shiver> Now, that’s weird. There’s nothing there, except there’s not even a there there, if you know what I mean.”

“I think I do, and you’ve just given us one more clue to where you almost went. Whoa, no more shivering, you’re back here safe where there’s normal matter and real locations, OK? <another soothing pause> That’s better. So, I was assuming a binary situation, an anti‑Universe obeying a Charge‑Parity‑Time symmetry that’s exactly the reverse of ours. The math allows only the two possibilities. You observed ‘no there there’ when you tried for a third option. That’s support for the assumption.”

“How could we have even two Universes?”

“It goes back to the high‑energy turmoil at the Big Bang’s singularity. Symmetry says the chaos in the singularity should have generated as many anti‑atoms, umm, as many positrons and anti‑protons, as their normal equivalents.”

“Positrons?”

“Anti‑electrons. Long story. The big puzzle is, where did those anti‑guys go? One proposal that’s been floating around is that while normal matter and our normal CPT symmetry expanded from the singularity to make our Universe, the anti‑matter and reversed symmetry expanded in some kind of opposite direction to make the anti‑Universe. You may have found that direction. Here, I’ll do a quick sketch on Old Reliable.”

“Looks like some of the banged‑up painted‑up battle shields I saw a thousand years ago.”

“It does, a little. Over on the top left is our normal‑matter Universe with galaxies and all, expanding out of the singularity at time zero. Time runs vertically upward from that point. I can’t draw three spatial dimensions so just one expanding sideways will have to do, OK?”

“No problem, I do x‑y‑z‑t thinking all the time when I use my superpower.”

“Of course you do. Well, coming down out of the singularity into minus‑time we’ve got the anti‑Universe. I’ve reversed the color scheme because why not, although I expect their colors would look exactly like ours because we know that photons are their own anti‑particles and should behave the same in both Universes.”

“They do. Anti‑Anne looked just like me, white satin and all.”

“Excellent, another clue. Anyway, see how minus‑time increases in the negative direction as the anti‑Universe expands just like plus‑time increases positively for us?”

“Mmm, yeah, but we only call them minus and plus because we’re standing outside of both of them. Looking from the inside, I’d say time in each increases towards expansion.”

“Good insight, you’re way ahead of me. That’s what I’ve drawn on the right side of the sketch. The two are perfectly equivalent except for CPT and anti‑CPT. Time direction, x‑y‑z space directions, even spin orientation, can all be made parallel between the two. However, the charges are reversed. Anti‑Anne’s atoms have positrons where we have electrons, negative anti‑protons where we have positive protons. When anti‑matter meets matter, there’s massive energy release from equivalent charged particles neutralizing each other.”

“Wait. Gravity. Wouldn’t anti‑matter particles repel each other? Your picture has galaxies and they couldn’t grow up with everything backwards.”

“Nope, you’re carrying this model too far. The only thing that’s reversed is charge. Masses work the same in each symmetry. Gravity pays attention to mass, not charge, and it’s always a force of attraction.”

“Anyway, not going back there.”

“Good.”

~~ Rich Olcott

Avoiding A Big Bang

On By rolcottIn Cosmology, UncategorizedLeave a comment

<fffshwwPOP!!> … <thump!> “Ow!”

That white satin dress, that molten‑silver voice. “Anne? Is that you? Are you OK?”

“Yeah, Sy, it’s me. I’m all right … I think.”

“What happened? Where’ve you been all year? Or considering it’s you I should ask, when’ve you been?”

“You know the line between history and archaeology?”

“Whether or not there was writing?”

“Sort of. Anyway, I’ve crossed it dozens of times. You wouldn’t believe some of the things I’ve seen. The professionals sure wouldn’t.”

“Wait, does the dress go with you? White satin wasn’t a thing centuries ago.”

“Oh, it changes like camouflage when I travel. That’s one reason I like this era — white satin’s so much nicer than muddy homespun or deerskins, mmm?”

“Mm‑hmmm. I suppose that’s why the dress didn’t get messed up when you erupted here. What led to that, anyway?”

“I don’t know. It probably had something to do with me experimenting with my ‘pushing’ superpower, going for a direction I hadn’t tried before. I’ve always known that front‑and‑back ‘pushing’ moves me forward or backward in time. You helped me understand that a ‘push’ to the side shifts me between alternate Universes at different probability levels. ‘Pushing’ up or down changes my size. Well, this morning I figured out a different direction to ‘push’ and that was weird.”

“You’ve described all three normal directions of space, so a new one would have to be weird.”

“I know what that direction feels like even if I can’t describe it. What was weird is what happened when I tried ‘pushing’ there. Things came into focus a little slowly. That may be what saved me. What I saw in front of me was … me. Dress, hair, everything, reflected left‑to‑right like looking in a mirror but our movements were a little different. Things were sharpening up and suddenly this sheet of fire flared between us and it blew me … here, to your office. What was all that about, Sy?”

“A couple of questions first. That sheet of fire — did it have a color or was it pure white?”

“Not white, more of a bright blue-violet.”

“And did it start like <snap> or were there preliminary sparkles?”

“Umm .. yes, there were sparkles! In fact I was already ‘pushing’ away when the bad flare‑up started. How did you know?”

“Just following a train of thought. I’m hypothesizing here, but I think you just barely escaped blowing the Earth apart.”

“WHAAATT!!?!”

“It all goes back to the Big Bang and our belief that physical phenomena have fundamental symmetries. Back in the Universe’s first few skillionths of a second the energy density was so high that the electromagnetic and nuclear forces were symmetry‑related. Any twitch in the chaotic unified force field was equally likely to become a proton or an anti‑proton, matter or anti‑matter. So why is anti‑matter so rare in our Universe?”

“Maybe the matter atoms just wiped out all the anti‑matter.”

“Uh‑uh. By symmetry, there should have been exactly as much of each sort. If the wipe‑out had happened there wouldn’t have been enough matter left over to make a single galaxy, much less billions of them. But here we are. Explaining that is one of the biggest challenges in cosmology.”

“You say ‘symmetry‘ like that’s a sacred principle.”

“I wouldn’t say ‘sacred‘ but the most accurate physical theory we know of is based on the product of Charge, Parity and Time symmetries being constant in our Universe. If you take a normal atom and somehow reverse both its charge and spin to get an anti‑matter atom, the symmetries say that the reversed atom must travel backward in time. From an outsider’s perspective it’d be like the original atom and the anti‑atom rush together, annihilate each other and release the enormous amount of energy that accomplished the reversal. Anne, I think you almost ‘pushed’ yourself into an anti‑Universe with a reversed CPT symmetry.”

“Those blue-violet flashes…”

“…were atoms from the air you carried with you, colliding with anti‑atoms in your anti‑twin’s air. Good thing those micro‑collisions released enough energy to get you back here before…”

“…I touched anti‑Anne or even breathed! <shiver> That would have been…”

“…BLOOEY!”

“This is nicer, mmm?”

~~ Rich Olcott

A Recourse to Pastry

On By rolcottIn Astronomy: Planetary Science, Astronomy: Techniques, Physics: Fundamentals, UncategorizedLeave a comment

There’s something wrong about the displays laid out on Al’s pastry counter — no symmetry.  One covered platter holds eight pinwheels in a ring about a central one, but the other platter’s central pinwheel has only a five-pinwheel ring around it.  I yell over to him.  “What’s with the pastries, Al?  You usually balance things up.”

“Ya noticed, hey, Sy?  It’s a tribute to the Juno spacecraft.  She went into orbit around Jupiter on the 5th of July 2016 so I’m celebrating her anniversary.”

“Well, that’s nice, but what do pinwheels have to do with the spacecraft?”

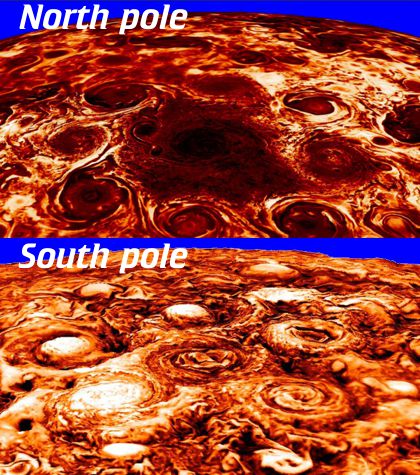“Haven’t you seen the polar pictures she sent back?  Got a new poster behind the cash register.  Ain’t they gorgeous?”Jupiter both poles“They’re certainly eye-catching, but I thought Jupiter’s all baby-blue and salmon-colored.”

Astronomer Cathleen’s behind me in line.  “It is, Sy, but only in photographs using visible sunlight.  These are infrared images, right, Al?”

“Yeah, from … lemme look at the caption … Juno‘s JIRAM instrument.”

“Right, the infrared mapper.  It sees heat-generated light that comes from inside Jupiter.  It’s the same principle as using blackbody radiation to take a star’s temperature, but here we’re looking at a planet.  Jupiter’s way colder than a star so the wavelengths are longer, but on the other hand it’s close-up so we don’t have to reckon with relativistic wavelength stretching.  At any rate, infrared wavelengths are too long for our eyes to see but they penetrate clouds of particulate matter like interstellar dust or the frigid clouds of Jupiter.”

Jupiter south pole 1
NASA mosaic view of Jupiter’s south pole by visible light

“So this red hell isn’t what the poles actually look like?”

“No, Al,  the visible light colors are in the tops of clouds and they’re all blues and white.  These infrared images show us temperature variation within the clouds.  Come to think of it, that Hell’s frozen over — if I recall correctly, the temperature range in those clouds runs from about –10°C to –80°C.  In Fahrenheit that’d be from near zero to crazy cold.”

“Those aren’t just photographs in Al’s poster?”

“Oh, no, Sy, there’s a lot of computer processing in between Juno‘s wavelength numbers and what the public sees.  The first step is to recode all the infrared wavelengths to visible colors.  In that north pole image I’d say that they coded red-to-black as warm down to white as cool.  The south pole image looks like warmest is yellow-to-white, coolest is red.”

“How’d you figure that?”

“The programs fake the apparent heights.  The warmest areas are where we can see most deeply into the atmosphere, which would be at the center or edge of a vortex.  The cooler areas would be upper-level material.  The techs use that logic to generate the perspective projection that we interpret as a 3-D view.”

Vinnie’s behind us in line and getting impatient.  “I suppose there’s Science in those pretty pictures?”

“Tons of it, and a few mysteries.  JIRAM by itself is telling the researchers a lot about where and how much water and other small molecules reside in Jupiter’s atmosphere.  But Juno has eight other sensors.  Scientists expect to harvest important information from each of them.  Correlations between the data streams will give us exponentially more.”

He’s still antsy.  “Such as?”

“Like how Jupiter’s off-axis magnetic field is related to its lumpy gravitational field.  When we figure that out we’ll know a lot more about how Jupiter works, and that’ll help us understand Saturn and gas-giant exoplanets.”GRS core

Al breaks in.  “What about the mysteries, Cathleen?”

“Those storms, for instance.  They look like Earth-style hurricanes, driven by upwelling warm air.  They even go in the right direction.  But why are they crammed together so and how can they stay stable like that?  Adjacent gears have to rotate in opposite directions, but these guys all go in the same direction.  I can’t imagine what the winds between them must be like.”

“And how come there’s eight in the north pole ring but only five at the other pole?”

“Who knows, Vinnie?  The only guess I have is that Jupiter’s so big that one end doesn’t know what the other end’s doing.”

“Someone’s gonna have to do better than that.”

“Give ’em time.”

~~ Rich Olcott

They Went That-away. But Why?

On By rolcottIn Physics: Electromagnetism, Physics: Fundamentals, UncategorizedLeave a comment

“It’s worse than that, Vinnie.”  I pull out Old Reliable, my math-monster tablet.  “Let me scan in that three-electron drawing of yours.”3 electrons in B-field

“Good enough to keep a record of it?”

“Nope, I want to exercise a new OVR app I just bought.”

“You mean OCR.”

“Uh-uh, this is Original Vector Reconstruction, not Optical Character Recognition.    OCR lets you read a document into a word processor so you can modify it.  OVR does the same thing but with graphics.  Give me a sec … there.  OK, look at this.”3 electrons in B-field revisited

“Cool, you turned my drawing 180°, sort of.  Nice app.  Oh, and you moved the red electron’s path so it’s going opposite to the blue electron instead of parallel to the magnetic field.  Why’d you bother?”

“See the difference between blue and red?”

“Well, yeah, one’s going up, one’s going down.  That’s what I came to you about and you shot down my theory.  Those B-arrows in the magnetic field are going in completely the wrong direction to push things that way.”

“Well, actually, they’re going in exactly the right direction for that, because a magnetic field pushes along perpendiculars.  Ever hear of The Right Hand Rule?”

“You mean like ‘lefty-loosey, righty-tighty’?”

“That works, too, but it’s not the rule I’m talking about.  If you point your thumb in the direction an electron is moving, and your index finger in the direction of the magnetic field, your third finger points in the deflection direction.  Try it.”

“Hurts my wrist when I do it for the blue one, but yeah, the rule works for that.  It’s easier for the red one.  OK, you got this rule, fine, but why does it work?”

“Part of it goes back to the vector math you don’t want me to throw at you.  Let’s just say that there are versions of a Right Hand Rule all over physics.  Many of them are essentially definitions, in the same way that Newton’s Laws of Motion defined force and mass.  Suppose you’re studying the movements directed by some new kind of force.  Typically, you try to define some underlying field in such a way that you can write equations that predict the movement.  You haven’t changed Nature, you’ve just improved our view of how things fit together.”

“So you’re telling me that whoever made that drawing I copied drew the direction those B-arrows pointed just to fit the rule?”

“Almost.  The intensity of the field is whatever it is and the lines minus their pointy parts are wherever they are.  The only thing we can set a rule for is which end of the line gets the arrowhead.  Make sense?”Spiraling electron

“I suppose.  But now I got two questions instead of the one I come in here with.  I can see the deflection twisting that electron’s path into a spiral.  But I don’t see why it spirals upward instead of downward, and I still don’t see how the whole thing works in the first place.”

“I’m afraid you’ve stumbled into a rabbit hole  we don’t generally talk about.  When Newton gave us his Law of Gravity, he didn’t really explain gravity, he just told us how to calculate it.  It took Einstein and General Relativity to get a deeper explanation.  See that really thick book on my shelf over there?  It’s loaded with tables of thermodynamic numbers I can use to calculate chemical reactions, but we didn’t start to understand those numbers until quantum mechanics came along.  Maxwell’s equations let us calculate electricity, magnetism and their interaction — but they don’t tell us why they work.”

“I get the drift.  You’re gonna tell me it goes up because it goes up.”

“That’s pretty much the story.  Electrons are among the simplest particles we know of.  Maxwell and his equations gave us a good handle on how they behave, nothing on why we have a Right Hand Rule instead of a Left Hand Rule.  The parity just falls out of the math.  Left-right asymmetry seems to have something to do with the geometry of the Universe, but we really don’t know.”

“Will string theory help?”

“Physicists have spent 50 years grinding on that without a testable result.  I’m not holding my breath.”

~~ Rich Olcott

Shells A-poppin’

On By rolcottIn Physics: Quantum Mechanics, Physics: Waves, UncategorizedLeave a comment

We step into Eddie’s.  Vinnie spots Jeremy behind the gelato stand.  “Hey, kid, you studying something Science-y?”

“Yessir, my geology text.”

“Lemme see it a sec, OK?”

“Sure.  Want a gelato?”

“Yeah, gimme a pistachio, double-dip.  I’ll hold your book while you’re doing that.  Ah-hah, Sy, lookie here, page 37 — new textbook but this atom diagram coulda come right out of that 1912 Bohr paper you don’t like.  See, eight dots in a ring around the nucleus.  Can’t be wrong or it wouldn’t have survived this long, right?”

<sigh>  “What it is isn’t what it was.  Bohr proposed his model as a way to explain atomic spectra.  We’ve got a much better model now — but the two agree on three points.  Atoms organize their electronic charge in concentric shells, innermost shells deepest in the nuclear energy well.  Second, each shell has a limited capacity.  Third, when charge moves from one shell to another, light energy is absorbed or emitted to match the energy difference between shells.  Beyond those, not much.  Here, this diagram hints at the differences.”Better Bohr

“The scrambled-looking half is the new picture?”

“Pure chaos, where the only thing you can be sure of is the averages.  These days the Bohr model survives as just an accounting device to keep track of how much charge is in each shell.  That diagram — what kind of atom is it describing?”

“I dunno, two electrons inside, eight outside, ten total.”

“Could be neon, or a fluoride, oxide, sodium or magnesium ion.  From a quantum perspective they all look the same.”

“Here’s your gelato, sir.”

“Thanks, kid, here’s your book back.  But those are different elements, Sy.”

“The important thing, Vinnie, is they all have an outer shell with eight units of charge.  That’s the most stable configuration.”

“What’s so special about eight, Mr Moire?  If it’s pure chaos shouldn’t any number be OK?”

“Like I said, Jeremy, it’s the averages that count.  Actually, this is one of my favorite examples of what Wigner called ‘The Unreasonable Effectiveness of Mathematics in the Natural Sciences.’  Back in 1782, a century and a quarter before anyone took atoms seriously, Laplace did some interesting math.  Have you ever waited for a pot of water to boil and spent the time tapping the pot to see the ripples?”

“Who hasn’t?  Doesn’t boil any faster, though.”

“True.  Looking at those waves, you saw patterns you don’t see with flat reflectors, right?”

“Oh, yeah — some like dumbbells, a lot of circles.”

“Mm-hm.  In a completely random situation all possible patterns could appear, but the pot’s circular boundary suppresses everything except wave patterns that match its symmetry.  You don’t see hexagons, for instance.”

“That’s right, I didn’t.”

“So there’s Laplace in the 1790s, thinking about Newton’s Law of Gravity, and he realizes that even in the boundaryless Solar System there’s still a boundary condition — any well-behaved standing wave has to have the same value at the central point no matter what direction you come from.  He worked out all the possible stable patterns that could exist in a central field like that.  Some of them look like what you saw in the water.  We now classify them by symmetry and node count.”

“Node?”Disk orbitals

“A region where the pattern hits zero, Vinnie.  Density waves range from zero to some positive value; other kinds range from positive to negative values.  A spherical wave could peak at the center and then go to zero infinitely far away.  One node.  Or it could be zero at the center, peak in a spherical shell some distance out and then fade away.  That’d be two nodes.  Or it could be zero at the center, zero far away, and have two peaks at different distances with a spherical third node in between.  Here’s another two-node pattern — that dumbbell shape with nodes at the center and infinity.  You can add radial nodes partway out.”

“I’m getting the picture.”

“Sure.  You might think Laplace’s patterns are just pretty pictures, but electron charge in atoms and ions just happens to collect in exactly those patterns.  Combine Laplace’s one-node and two-node patterns, you get the two lowest-energy stable shells.  They hold exactly ten charge units.  The energies are right, too.  Effective?”

“Unreasonably.”

~~ Rich Olcott

Fifty Shades of Ice

On By rolcottIn Astronomy: Planetary Science, Chemistry, UncategorizedLeave a comment

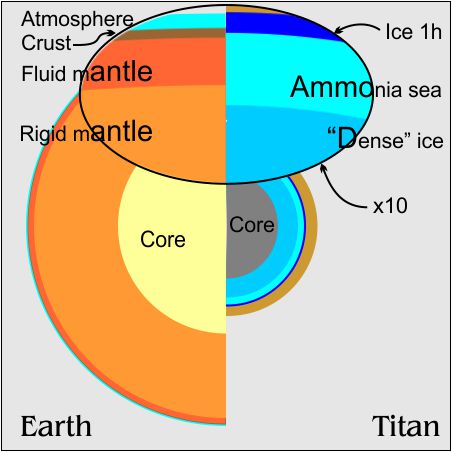
earth-vs-titan-sea

This week we dip a little deeper into Titan’s weirdness trove.  Check the diagram.  Two kinds of ice??!?  What’s that about?

diamond-and-ice
Carbon allotropes
and water polymorphs

As everyone knows, diamonds and pencil lead (graphite, and I loved learning that graphite is an actual dug-from-the-ground mineral whose name came from the Greek verb “to write”) are both pure carbon, mostly.  Same atoms, just arranged differently.

Graphite‘s carbon atoms are laid out in sheets of hexagons.  Adjacent sheets are bonded together but not as strongly as are the atoms within each sheet.  Sheets can slide past each other, which is why we use graphite as a lubricant and why pencils can write and erasers can unwrite.

Diamond‘s atoms are also laid out in sheets of (rumpled) hexagons, but now the bonds between sheets are identical to the bonds within a sheet.  Turn your head sideways and you’ll see that sheets run vertical, too.  In fact, each carbon atom participates in four sheets, three vertical and one horizontal.  All that symmetrical bonding makes diamond one of the hardest substances we know of.

Neighboring carbon atoms form bonds by sharing electrons between their positive nuclei.  Neighboring water molecules (H2O) don’t share electrons but they do tend to line up with their somewhat positive hydrogen atoms pointing towards nearby somewhat negative oxygens.  That’s a loose rule in liquid water but it dominates when the molecules freeze into ice.

Most of the ice on Earth has an Ice-Ih structure, where the oxygen atoms are arranged in the same pattern as the carbons are in graphite.  Water’s hexagonal sheets aren’t quite flat, but the 6-fold symmetry gives us snowflakes.  There’s a hydrogen atom between each pair of oxygens, but it’s not half-way between.  Instead, each oxygen tightly holds its own two hydrogens while it pulls at further-away hydrogens owned by two neighboring oxygens.

But water molecules have other ways to arrange themselves.  A small fraction of Earth’s ice has a diamond-like Ice-Ic structure with each oxygen participating in four hexagon sheets.  Again, hydrogens are on the lines between them.

Water’s such a versatile molecule that it doesn’t stop with two polymorphs.  Ice scientists recognize seventeen distinct crystalline varieties, plus three where the molecules don’t line up neatly.  (None of them is Vonnegut’s “Ice-nine.”)  Each polymorph exists in a  unique temperature and pressure range; each has its own set of properties.  As you might expect, ices formed at high pressure are denser than liquid water.  Fortunately, Ice-Ih is lighter than water and so ice cubes and icebergs float.

As cold as Titan is and as high as the pressure must be under 180 miles of Ice-Ih and watery ammonia sea (even at 10% of Earth’s gravity), it’s quite likely* that there’s a thick layer of Ice-something around Titan’s rocky core.

clathratesThe primary reason we think Titan is so wet is that Titan’s density is about halfway between rock and water.  We know there are other light molecules on Titan — ammonia, methane, etc.  We don’t know how much of each.  Those compounds don’t have water’s complex phase behavior but many can dissolve in it.  That’s why that hypothetical “Ammonia sea” is in the top diagram.

But wait, there’s more.  Both graphite and water ice are known to form complex polymorphs, clathrates, that host other molecules.  This diagram gives a hint of how that can happen.  Frozen water under pressure forms a large number of more-or-less ordered cage clathrate structures that can host  Titan’s molecular multitude.

At Titan’s temperatures ice rocks would be about as hard as granite.  Undoubtedly they’ll have surprising chemistry and interesting histories.  We can expect clathrate geology on Titan to be as complex as silicate geology is on Earth.

Geochemist heaven, except for the space suits.

~~ Rich Olcott

* – A caveat: we know a great deal about Earth’s structure because we live here and have been studying it scientifically for centuries. On the other hand, most of what we think we know about Titan’s interior comes from mathematical models based on gravitational observations from the Cassini mission, plus 350 photos relayed back from the Huygens lander, plus experiments in Earth-bound chemistry labs. Expect revisions on some of this stuff as we learn more.