Tag: Inertial frame

Which Way Is Up?

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Fundamentals, Space Travel, UncategorizedLeave a comment

“OK, Moire, the Attitude Control System’s reaction wheels swing James Webb Space Telescope through whatever angle changes it wants, but how does ACS know what direction JWST‘s at to begin with? Does it go searching through that million‑star catalog to find something that matches?”

“Hardly, Mr Feder, that’d be way too much work for a shipboard computer. No, ACS consults the orientations maintained by a set of gyroscopes that are mounted on JWST‘s framework. Each one points along an unvarying bearing relative to the Universe, no matter how the satellite’s situated.”

“Gyroscopes? Like the one I had as a kid? Winding the string around the axle was a pain and then however hard I pulled the string I couldn’t keep one going for more than half a minute. It always wobbled anyway. Bad choice.”

“Not the JWST choice, NASA mostly doesn’t do toys. Actually, the gyroscope you remember has a long and honorable history. Gimbals have been known and used in one form or another for centuries. A few researchers mounted a rotor inside a gimbal set for various purposes in the mid‑1800s, but it was Léon Foucault who named his gadget a gyroscope when he used one for a public demonstration of the Earth’s rotation. People used to go to lectures like we go to a show. Science was popular in those days.”

“Wait — Foucault? The pendulum guy?”
 ”Wait — Foucault? The knife‑edge test guy?”

“Our science museum used to have a big pendulum. I loved to watch it knock down those domino thingies one by one as it turned around its circle. Then they took it out to make room for another dinosaur or something.”

“Yup. A museum’s most precious resource is floorspace. That weight swinging on a long wire takes up a lot of square feet. Foucault’s pendulum was another of his Earth‑rotation demonstrations, just a year after the gyroscope show. Yeah, Al, same guy — Foucault invented that technique you use to check your telescope mirrors. He pioneered a lot of Physics. He showed that the absorption spectrum of a gas when a light shines through it matches the spectrum it emits when you heat it up. His lightspeed measurement came within one percent of our currently accepted value. ”

Astronomer Cathleen shakes her head. “Imagine, 200 years after Kepler and Newton, yet people in Foucault’s day still needed convincing that the Earth is a globe floating in space. A century and a half later some still do. <sigh> Funny, isn’t it, how Foucault was working at the same time on two such different phenomena.”

“Not so different, Cathleen. Both demonstrate the same underlying principle — inertia relates to the Universe and doesn’t care about local conditions. Foucault was really working on inertia. He made use of two different inertial effects for his demonstrations. By the way, Mr Feder, the pendulum doesn’t turn. The Earth turns beneath the pendulum to bring those domino thingies into target position.”

“That’s hard to believe.”

“Could be why his demonstrations used two different phenomena. Given 19th Century technology, those were probably his best options.”

“If only he’d had lasers, huh?”

“One kind of modern gyroscope is laser‑based. Uses photons going around a ring. Actually, photons or pulses of them going around the same ring in opposite directions. When the ring itself rotates, the photons or pulses going against the rotation encounter the Start point sooner than their opposites do. Time the difference and you can figure the rotation rate. Unfortunately, Foucault didn’t have lasers or the exquisite timing devices we have today. But that’s not the kind of gyroscope JWST carries, anyway.”

“OK, I’ll bite. What does it use?”

“The slickest one yet, Al. If you carefully tap the rim of a good wine glass it’ll vibrate like the red line here. The dotted blue circle’s the glass at rest. Under the right conditions inertia holds the planes of vibration steady even if the glass itself rotates. People have figured out how to use that principle to build extremely accurate. reliable and low‑maintenance gyroscopes for measuring and stabilizing rotations. JWST carries a set.”

“Nothing to lubricate, eh?”

Portrait of Léon Foucault from Wikimedia under Creative Commons Attribution 3.0 Unported license.

~~ Rich Olcott

Turn This Way to Turn That Way

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Physics: Newton and Gravity, Space Travel, UncategorizedLeave a comment

“I don’t understand, Sy. I get that James Webb Space Telescope uses its reaction wheels like a ship uses a rudder to change direction by pushing against something outside. Except the rudder pushes against water but the reaction wheels push against … what, the Universe?”

“Maybe probably, Al. We simply don’t know how inertia works. Newton just took inertia as a given. His Laws of Motion say that things remain at rest or persist in linear motion unless acted upon by some force. He didn’t say why. Einstein’s General Relativity starts from his Equivalence Principle — gravitational inertia is identical to mechanical inertia. That’s held up to painstaking experimental tests, but why it works is still an open question. Einstein liked Mach’s explanation, that we experience these inertias because matter interacts somehow with the rest of the Universe. He didn’t speculate how that interaction works because he didn’t like Action At A Distance. The quantum field theory people say that everything’s part of the universal field structure, which sounds cool but doesn’t help much. String theory … ’nuff said.”

“Hey, Moire, what’s all that got to do with the reaction wheel thing? JWST can push against one all it wants but it won’t go anywhere ’cause the wheel’s inside it. What’s magic about the wheels?”

“JWST doesn’t want to go anywhere else, Mr Feder. We’re happy with it being in its proper orbit, but it needs to be able to point to different angles. Reaction wheels and gyroscopes are all about angular momentum, not about the linear kind that’s involved with moving from place to place.”

“HAH! JWST is moving place to place, in that orbit! Ain’t it got linear momentum then?”

Newton’s Principia, Proposition II, Theorem II

“In a limited way, pun intended. Angular momentum is linear momentum plus a radial constraint. This goes back to Newton and his Principia book. I’ve got a copy of his basic arc‑splitting diagram here in Old Reliable. The ABCDEF line is a section of some curve around point S. He treated it as a succession of short line segments ABc, BCd, CDe and so on. If JWST is at point B, for instance, Newton would say that it’s traveling with a certain linear momentum along the BCd line. However, it’s constrained to move along the arc so it winds up at D instead d. To account for the constraint Newton invented centripetal force to pull along the Sd line. He then mentally made the steps smaller and smaller until the sequence of short lines matched the curve. At the limit, a sequence of little bits of linear momentum becomes angular momentum. By the way, this step‑reduction process is at the heart of calculus. Anyway, JWST uses its reaction wheels to swing itself around, not to propel itself.”

“And we’re back to my original question, Sy. What makes that swinging happen?”

“Oh, you mean the mechanical reality. Easy, Al. Like I said, three pairs of motorized wheels are mounted on JWST‘s frame near the center of mass. Their axles are at mutual right angles. Change a wheel’s angular momentum, you get an equal opposing change to the satellite’s. Suppose the Attitude Control System wants the satellite to swing to starboard. That’d be clockwise viewed from the cold side. ACS must tell a port/starboard motor to spin its wheel faster counterclockwise. If it’s already spinning clockwise, the command would be to put on the brakes, right? Either way, JWST swings clockwise. With the forward/aft motors and the hot‑side/cold‑side motors, the ACS is equipped to get to any orientation. See how that works?”

“Hang on.” <handwaving ensues> “Yeah, I guess so.”

“Hey, Moire. What if the wheel’s already spinning at top speed in the direction the ACS wants more of?”

“Ah, that calls for a momentum dump. JWST‘s equipped with eight small rocket engines called thrusters. They convert angular momentum back to linear momentum in rocket exhaust. Suppose we need a further turn to starboard but a port/starboard wheel is nearing threshold spin rate. ACS puts the brakes on that wheel, which by itself would turn the satellite to port. However, ACS simultaneously activates selected thrusters to oppose the portward slew. Cute, huh?”

~~ Rich Olcott

Attitude Adjustment

On By rolcottIn Astronomy: Techniques, James Webb Space Telescope, Space Travel, UncategorizedLeave a comment

Mr Feder has a snarky grin on his face and a far‑away look in his eye. “Got another one. James Webb Space Telescope flies in this big circle crosswise to the Sun‑Earth line, right? But the Earth doesn’t stand still, it goes around the Sun, right? The circle keeps JWST the same distance from the Sun in maybe January, but it’ll fly towards the Sun three months later and get flung out of position.” <grabs a paper napkin> “Lemme show you. Like this and … like this.”

“Sorry, Mr Feder, that’s not how either JWST or L2 works. The satellite’s on a 6-month orbit around L2 — spiraling, not flinging. Your thinking would be correct for a solid gyroscope but it doesn’t apply to how JWST keeps station around L2. Show him, Sy.”

“Gimme a sec with Old Reliable, Cathleen.” <tapping> “OK, here’s an animation over a few months. What happens to JWST goes back to why L2 is a special point. The five Lagrange points are all about balance. Near L2 JWST will feel gravitational pulls towards the Sun and the Earth, but their combined attraction is opposed by the centrifugal force acting to move the satellite further out. L2 is where the three balance out radially. But JWST and anything else near the extended Sun‑Earth line are affected by an additional blended force pointing toward the line itself. If you’re close to it, sideways gravitational forces from the Sun and the Earth combine to attract you back towards the line where the sideways forces balance out. Doesn’t matter whether you’re north or south, spinward or widdershins, you’ll be drawn back to the line.”

Al’s on refill patrol, eavesdropping a little of course. He gets to our table, puts down the coffee pot and pulls up a chair. “You’re talking about the JWST. Can someone answer a question for me?”

“We can try.”
 ”What’s the question?”
  Mr Feder, not being the guy asking the question, pooches out his lower lip.

“OK, how do they get it to point in the right direction and stay there? My little backyard telescope gives me fits just centering on some star. That’s while the tripod’s standing on good, solid Earth. JWST‘s out there standing on nothing.”

“JWST‘s Attitude Control System has a whole set of functions to do that. It monitors JWST‘s current orientation. It accepts targeting orders for where to point the scope. It computes scope and satellite rotations to get from here to there. Then it revises as necessary in case the first‑draft rotations would swing JWST‘s cold side into the sunlight. It picks a convenient guide star from its million‑star catalog. Finally, ACS commands its attitude control motors to swing everything into the new position. Every few milliseconds it checks the guide star’s image in a separate sensor and issues tweak commands to keep the scope in proper orientation.”

“I get the sequence, Sy, but it doesn’t answer the how. They can’t use rockets for all that maneuvering or they’d run out of fuel real fast.”

“Not to mention cluttering up the view field with exhaust gases.”

“Good point, Cathleen. You’re right, Al, they don’t use rockets, they use reaction wheels, mostly.”

“Uh-oh, didn’t broken reaction wheels kill Kepler and a few other missions?”

“That sounds familiar, Mr Feder. What’s a reaction wheel, Sy, and don’t they put JWST in jeopardy?”

 Gyroscope, image by Lucas Vieira

“A reaction wheel is a massive doughnut that can spin at high speed, like a classical gyroscope but not on gimbals.”

“Hey, Moire, what’s a gimbal?”

“It’s a rotating frame with two pivots for something else that rotates. Two or three gimbals at mutual right angles let what’s inside orient independent of what’s outside. The difference between a classical gyroscope and a reaction wheel is that the gyroscope’s pivots rotate freely but the reaction wheel’s axis is fixed to a structure. Operationally, the difference is that you use a gyroscope’s angular inertia to detect change of orientation but you push against a reaction wheel’s angular inertia to create a change of orientation.”

“What about the jeopardy?”

“Kepler‘s failing wheels used metal bearings. JWST‘s are hardened ceramic.”

<whew>

~~ Rich Olcott

Hyperbolas But Not Hyperbole

On By rolcottIn Astronomy: Techniques, Physics: Light and Relativity, Uncategorized2 Comments

“Minus? Where did that come from?”

<Gentle reader — If that question looks unfamiliar, please read the preceding post before this one.>

Jim’s still at the Open Mic. “A clever application of hyperbolic geometry.” Now several of Jeremy’s groupies are looking upset. “OK, I’ll step back a bit. Jeremy, suppose your telescope captures a side view of a 1000‑meter spaceship but it’s moving at 99% of lightspeed relative to you. The Lorentz factor for that velocity is 7.09. What will its length look like to you?”

“Lorentz contracts lengths so the ship’s kilometer appears to be shorter by that 7.09 factor so from here it’d look about … 140 meters long.”

“Nice, How about the clocks on that spaceship?”

“I’d see their seconds appear to lengthen by that same 7.09 factor.”

“So if I multiplied the space contraction by the time dilation to get a spacetime hypervolume—”

“You’d get what you would have gotten with the spaceship standing still. The contraction and dilation factors cancel out.”

“How about if the spaceship went even faster, say 99.999% of lightspeed?”

“The Lorentz factor gets bigger but the arithmetic for contraction and dilation still cancels. The hypervolume you defined is always gonna be just the product of the ship’s rest length and rest clock rate.”

His groupies go “Oooo.”

One of the groupies pipes up. “Wait, the product of x and y is a constant — that’s a hyperbola!”

“Bingo. Do you remember any other equations associated with hyperbolas?”

“Umm… Yes, x2–y2 equals a constant. That’s the same shape as the other one, of course, just rotated down so it cuts the x-axis vertically.”

Jeremy goes “Oooo.”

Jim draws hyperbolas and a circle on the whiteboard. That sets thoughts popping out all through the crowd. Maybe‑an‑Art‑major blurts into the general rumble. “Oh, ‘plus‘ locks x and y inside the constant so you get a circle boundary, but ‘minus‘ lets x get as big as it wants so long as y lags behind!”

Another conversation – “Wait, can xy=constant and x2–y2=constant both be right?”
  ”Sure, they’re different constants. Both equations are true where the red and blue lines cross.”

A physics student gets quizzical. “Jim, was this Minkowski’s idea, or Einstein’s?”

“That’s a darned good question, Paul. Minkowski was sole author of the paper that introduced spacetime and defined the interval, but he published it a year after Einstein’s 1905 Special Relativity paper highlighted the Lorentz transformations. I haven’t researched the history, but my money would be on Einstein intuitively connecting constant hypervolumes to hyperbolic geometry. He’d probably check his ideas with his mentor Minkowski, who was on the same trail but graciously framed his detailed write‑up to be in support of Einstein’s work.”

One of the astronomy students sniffs. “Wait, different observers see the same s2=(ct)2–d2 interval between two events? I suppose there’s algebra to prove that.”

“There is.”

“That’s all very nice in a geometric sort of way, but what does s2 mean and why should we care whether or not it’s constant?”

“Fair questions, Vera. Mmm … you probably care that intervals set limits on what astronomers see. Here’s a Minkowski map of the Universe. We’re in the center because naturally. Time runs upwards, space runs outwards and if you can imagine that as a hypersphere, go for it. Light can’t get to us from the gray areas. The red lines, they’re really a hypercone, mark where s2=0.”

From the back of the room — “A zero interval?”

“Sure. A zero interval means that the distance between two events exactly equals lightspeed times light’s travel time between those events. Which means if you’re surfing a lightwave between two events, you’re on an interval with zero measure. Let’s label Vera’s telescope session tonight as event A and her target event is B. If the A–B interval’s ct difference is greater then its d difference then she can see B — if the event is in our past but not beyond the Cosmic Microwave Background. But if a Dominion fleet battle is approaching us through subspace from that black dot, we’ll have no possible warning before they’re on us.”

Everyone goes “Oooo.”

~~ Rich Olcott

Thinking in Spacetime

On By rolcottIn Cosmology, Mathematics: Dimensions, UncategorizedLeave a comment

The Open Mic session in Al’s coffee shop is still going string. The crowd’s still muttering after Jeremy stuck a pin in Big Mike’s “coincidence” balloon when Jim steps up. Jim’s an Astrophysics post‑doc now so we quiet down expectantly. “Nice try, Mike. Here’s another mind expander to play with. <stepping over to the whiteboard> Folks, I give you … a hypotenuse. ‘That’s just a line,’ you say. Ah, yes, but it’s part of some right triangles like … these. Say three different observers are surveying the line from different locations. Alice finds her distance to point A is 300 meters and her distance to point B is 400. Applying Pythagoras’ Theorem, she figures the A–B distance as 500 meters. We good so far?”

A couple of Jeremy’s groupies look doubtful. Maybe‑an‑Art‑Major shyly raises a hand. “The formula they taught us is a2+b2=c2. And aren’t the x and y supposed to go horizontal and vertical?”

“Whoa, nice questions and important points. In a minute I’m going to use c for the speed of light. It’s confusing to use the same letter for two different purposes. Also, we have to pay them extra for double duty. Anyhow, I’m using d for distance here instead of c, OK? To your next point — Alice, Bob and Carl each have their own horizontal and vertical orientations, but the A–B line doesn’t care who’s looking at it. One of our fundamental principles is that the laws of Physics don’t depend on the observer’s frame of reference. In this situation that means that all three observers should measure the same length. The Pythagorean formula works for all of them, so long as we’re working on a flat plane and no-one’s doing relativistic stuff, OK?”

Tentative nods from the audience.

“Right, so much for flat pictures. Let’s up our game by a dimension. Here’s that same A–B line but it’s in a 3D box. <Maybe‑an‑Art‑Major snorts at Jim’s amateur attempt at perspective.> Fortunately, the Pythagoras formula extends quite nicely to three dimensions. It was fun figuring out why.”

Jeremy yells out. “What about time? Time’s a dimension.”

“For sure, but time’s not a length. You can’t add measurements unless they all have the same units.”

“You could fix that by multiplying time by c. Kilometers per second, times seconds, is a length.” His groupies go “Oooo.”

“Thanks for the bridge to spacetime where we have four coordinates — x, y, z and ct. That makes a big difference because now A and B each have both a where and a when — traveling between them is traveling in space and time. Computationally there’s two paths to follow from here. One is to stick with Pythagoras. Think of a 4D hypercube with our A–B line running between opposite vertices. We’re used to calculating area as x×y and volume as x×y×z so no surprise, the hypercube’s hypervolume is x×y×z×(ct). The square of the A–B line’s length would be b2=(ct)2+d2. Pythagoras would be happy with all of that but Einstein wasn’t. That’s where Alice and Bob and Carl come in again.”

“What do they have to do with it?”

“Carl’s sitting steady here on good green Earth, red‑shifted Alice is flying away at high speed and blue‑shifted Bob is flashing toward us. Because of Lorentz contractions and dilations, they all measure different A–B lengths and durations. Each observer would report a different value for b2. That violates the invariance principle. We need a ruggedized metric able to stand up to that sort of punishment. Einstein’s math professor Hermann Minkowski came up with a good one. First, a little nomenclature. Minkowski was OK with using the word ‘point‘ for a location in xyz space but he used ‘event‘ when time was one of the coordinates.”

“Makes sense, I put events on my calendar.”

“Good strategy. Minkowski’s next step quantified the separation between two events by defining a new metric he called the ‘interval.’ Its formula is very similar to Pythagoras’ formula, with one small change: s2=(ct)2–d2. Alice, Bob and Carl see different distances but they all see the same interval.”

“Minus? Where did that come from?”

~~ Rich Olcott

Speed Limit

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Wait, Sy, there’s something funny about that Lorentz factor. I’m riding my satellite and you’re in your spaceship to Mars and we compare notes and get different times and lengths and masses and all so we have to use the Lorentz factor to correct numbers between us. Which velocity do we use, yours or mine?”

“Good question, Vinnie. We use the difference between our two frames. We can subtract either velocity from the other one and replace v with that number. Strictly speaking, we’d subtract velocity components perpendicular to the vector between us. If I were to try to land on your satellite I’d have to expend fuel and energy to change my frame’s velocity to yours. When we matched frames the velocity difference would be zero, the Lorentz factor would be 1.0 and I’d see your solar array as a perfect 10×10‑meter square. Our clocks would tick in sync, too.”

“OK, now there’s another thing. That Lorentz formula compares our subtracted speeds to lightspeed c. What do we subtract to get c?”

“Deep question. That’s one of Einstein’s big insights. Suppose from my Mars‑bound spaceship I send out one light pulse toward Mars and another one in the reverse direction, and you’re watching from your satellite. No matter how fast my ship is traveling, Einstein said that you’d see both pulses, forward and backward, traveling at the same speed, c.”

“Wait, shouldn’t that be that your speed gets added to one pulse and subtracted from the other one?”

“Ejected mass works that way, but light has no mass. It measures its speed relative to space itself. What you subtract from c is zero. Everywhere.”

“OK, that’s deep. <pause> But another ‘nother thing—”

“For a guy who doesn’t like equations, you’re really getting into this one.”

“Yeah, as I get up to speed it grows on me. HAW!”

“Nice one, you got me. What’s the ‘nother thing?”

“I remembered how velocity is speed and direction but we’ve been mixing them together. If my satellite’s headed east and your spaceship’s headed west, one of us is minus to the other, right? We’re gonna figure opposite v‑numbers. How’s that work out?”

“You’re right. Makes no difference to the Lorentz factor because the square of a negative difference is the same as the square of its positive twin. You bring up an important point, though — the factor applies to both of us. From my frame, your clock is running slow. From your frame, mine’s the slow one. Einstein’s logic says we’re both right.”

“So we both show the same wrong time, no problem.”

“Nope, you see my clock running slow relative to your clock. I see exactly the reverse. But it gets worse. How about getting your pizza before you order it?”

“Eddie’s good, he ain’t that good. How do you propose to make that happen?”

“Well, I don’t, but follow me here. <working numbers on Old Reliable> Suppose we’re both in spaceships. I’m loafing along at 0.75c relative to Eddie’s pizza place on Earth and your ship is doing 3c. Also, suppose that we can transmit messages and mass much faster than lightspeed.”

“Like those Star Trek transporters and subspace radios.”

“Right. OK, at noon on my personal clock you tell me you’ve ordered pizza so I get one, too. Eddie slaps both our pizzas into his transporter 10 minutes later. The math works out that according to my clock you get your pizza 8.9 minutes before you put in your order. You like that?”

“Gimme a sec … nah, I don’t think so. If I read that formula right with v1 being you and v2 being me, if you run that formula for what I’d see with my velocity on the bottom, that’s a square root of a minus which can’t be right.”

“Yup, the calculation gives an imaginary number, 4.4i minutes, whatever that means. So between us we have two results that are just nonsense — I see effect before cause and you see a ridiculous time. To avoid that sort of thing, Einstein set his speed limit for light, gravity and information.”

“I’m willing to keep under it if you are.”

“Deal.”

~~ Rich Olcott

The Relativity Factor

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“Sy, it’s nice that Einstein agreed with Rayleigh’s wave theory stuff but why’d you even drag him in? I thought the faster‑than‑light thing was settled.”

“Vinnie, faster‑than‑light wasn’t even an issue until Einstein came along. Science had known lightspeed was fast but not infinite since Rømer measured it in Newton’s day. ‘Pretty fast,’ they said, but Newtonian mechanics is perfectly happy with any speed you like. Then along came Einstein.”

“Speed cop, was he?”

“Funny, Vinnie. No, Einstein showed that the Universe enforces the lightspeed limit. It’s central to how the Universe works. Come to think of it, the crucial equation had been around for two decades, but it took Einstein to recognize its significance.”

“Ah, geez, equations again.”

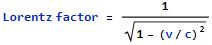
“Just this one and it’s simple. It’s all about comparing v for velocity which is how fast something’s going, to c the speed of light. Nothing mystical about the arithmetic — if you’re going half the speed of light, the factor works out to 1.16. Ninety‑nine percent of c gives you 7.09. Tack on another 9 and you’re up to 22.37 and so on.”

“You got those numbers memorized?”

“Mm-hm, they come in handy sometimes.”

“Handy how? What earthly use is it? Nothing around here goes near that fast.”

“Do you like your GPS? It’d be useless if the Lorentz factor weren’t included in the calculations. The satellites that send us their sync signals have an orbit about 84 000 kilometers wide. They run that circle once a sidereal day, just shy of 86 400 seconds. That works out to 3 kilometers per second and a Lorentz factor of 1.000 005.”

“Yeah, so? That’s pretty close to 1.0.”

“It’s off by 5 parts per million. Five parts per million of Earth’s 25 000-mile circumference is an eighth of a mile. Would you be happy if your GPS directed you to somewhere a block away from your address?”

“Depends on why I’m going there, but I get your point. So where else does this factor come into play?”

“Practically anywhere that involves a precision measurement of length or duration. It’s at the core of Einstein’s Special Relativity work. He thought about observing a distant moving object. It’s carrying a clock and a ruler pointed along the direction of motion. The observer would see ticks of the clock get further apart by the Lorentz factor, that’s time dilation. Meanwhile, they’d see the ruler shrink by the factor’s inverse, that’s space compression.”

“What’s this ‘distant observer‘ business?”

“It’s less to do with distance than with inertial frames. If you’re riding one inertial frame with a GPS satellite, you and your clock stay nicely synchronized with the satellite’s signals. You’d measure its 1×1‑meter solar array as a perfect square. Suppose I’m riding a spaceship that’s coasting to Mars. I measure everything relative to my own inertial frame which is different from yours. With my telescope I’d measure your satellite’s solar array as a rectangle, not a square. The side perpendicular to the satellite’s orbit would register the expected 1 meter high, but the side pointing along the orbit would be shorter, 1 meter divided by the Lorentz factor for our velocity difference. Also, our clocks would drift apart by that Lorentz factor.”

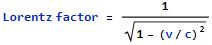
“Wait, Sy, there’s something funny about that equation.”

“Oh? What’s funny?”

“What if somebody’s speed gets to c? That’d make the bottom part zero. They didn’t let us do that in school.”

“And they shouldn’t — the answer is infinity. Einstein spotted the same issue but to him it was a feature, not a bug. Take mass, for instance. When they meet Einstein’s famous E=mc² equation most people think of the nuclear energy coming from a stationary lump of uranium. Newton’s F=ma defined mass in terms of a body’s inertia — the greater the mass, the more force needed to achieve a certain amount of acceleration. Einstein recognized that his equation’s ‘E‘ should include energy of motion, the ½mv² kind. He had to adjust ‘m‘ to keep F=ma working properly. The adjustment was to replace inertial mass with ‘relativistic mass,’ calculated as inertial mass times the Lorentz factor. It’d take infinite force to accelerate any relativistic mass up to c. That’s why lightspeed’s the speed limit.”

~~ Rich Olcott

Chasing Rainbows

On By rolcottIn Physics: Light and Relativity, UncategorizedLeave a comment

“C’mon, Sy, Newton gets three cheers for tying numbers to the rainbow’s colors and all that, but what’s it got to do with that three speeds of light thing which is where we started this discussion?”

“Vinnie, they weren’t just numbers, they were angles. The puzzle was why each color was bent to a different degree when entering or leaving the prism. That was an inconvenient truth for Newton.”

“Inconvenient? There’s a loaded word.”

“Indeed. A little context — Newton was in a big brouhaha about whether light was particles or waves. Newton was a particle guy all the way, battling wave theory proponents like Euler and Descartes and their followers on the Continent. Even Hooke in London had a wave theory. Newton’s problem was that his beam deflections happened right at the prism’s air‑glass interfaces.”

“What difference does that … wait, you mean that there’s no bending inside the prism? Light inside still goes straight but in a different direction?”

“That’s it, exactly. The deflection angles are the same, whether the beam hits the prism near the short‑path tip or the long‑path base. No evidence of further deviation inside the prism unless it has bubbles — Newton had to discard or mask off some bad prisms. Explaining the no‑curvature behavior is difficult in a particle framework, easy in a wave framework.”

“Really? I don’t see why.”

Left: faster medium, right: slower medium
Credit: Ulflund, under Creative Commons 1.0

“Suppose light is particles, which by definition are local things affected only by local forces. The medium’s effects on a particle would happen in the bulk material rather than at the interface. The effect would accumulate as the particles travel further through the medium. The bend should be a curve. Unfortunately for Newton, that’s not what his observations showed.”

“OK, scratch particles. Why not scratch waves, too?”

“Waves have no problem with abrupt variation at an interface, They flip immediately to a new stable mode. For example. here’s an animation showing an abrupt speed change at the interface between a fast‑travel medium like air and a slow‑travel medium like glass or water. See how one end of each bar gets slowed down while the other end is still moving at speed? By the time the whole bar is inside, its path has slewed to the refraction angle.”

“Like a car sliding on ice when a rear wheel sticks for an moment, eh Sy?”

“That was not a fun ride, Vinnie.”

“I enjoyed it. Whatever, I get how going air‑to‑glass or vice‑versa can change a beam’s direction. But if everything’s going through the same angle, how do rainbows happen?”

“Everything doesn’t go through the same angle. Frequencies make a difference. Go back to the video and keep your eye on one bar as it sweeps up the interface. See how the sweep’s speed controls the deflection angle?”

“Yeah, if the sweep went slower the beam would get a chance to bend further. Faster sweeps would bend it less. But what could change the sweep speed?

“Two things. One, change the medium to one with a different transmission speed. Two, change the wave itself so it has a different speed. According to Snell’s Law, the important parameter for a pair of media is their ratio of fast‑speed divided by slow‑speed. If the fast medium is a vacuum that ratio is the slow medium’s index of refraction. The greater the index, the greater the bend.”

“Changing the medium doesn’t apply. I got one prism, it’s got one index, but I still get a whole rainbow.”

“Right, rainbows are about how one prism treats a bunch of waves with different time and space frequencies.”

“Space frequency?”

“If you measure a wave in meters it’s cycles per meter.”

“Wavelength upside down. Got it.”

“Whether you figure in frequencies or intervals, the wave speed works out the same.”

“Speed of light, finally.”

“Point is, when a wave goes through any medium, its time frequency doesn’t change but its space frequency does. Interaction with local charge shortens the wavelength. Short‑wavelength blue waves are held back more than long‑wavelength red ones. The different angles make your rainbow. The hold‑back is why refraction indices are usually greater than one.”

“Usually?”

~~ Rich Olcott

Several Big Sloshes

On By rolcottIn Astronomy: Planetary Science, UncategorizedLeave a comment

“I call distraction, Sy. You were going to explain how come the Moon’s drifting away from us but you got us into radians and stuff. What’s that got to do with the Moon flying away by dragging a big wave around the Earth?”

“It’s not dragging a localized bulge of water like you’re thinking, Vinnie, nothing like that wave on Miller’s Planet. For that matter, the Miller’s Planet wave had a sharply‑rising front which also doesn’t look like the textbook tidal bulge.”

“There’s a textbook on this stuff?”

“Many, Al. Heavy-duty people have spent a lot of time on tides. Think about all the military and commercial navies that depend on boats being able to leave port and dock on schedule.”

“And not run aground <heh heh>”

“Well, yes, Vinnie. Anyhow, like a lot of pre‑computer Physics, that work was based on a simplified ideal system — a moon orbiting a smooth planet with a world‑covering ocean. Water’s drawn horizontally towards the sub‑lunar points making an egg‑shaped surface and everything’s neat.”

“Probably nothing like real life.”

“Of course. Here’s a video I built from satellite altimetry data. The grey dot is roughly the point underneath the Moon as that day progressed. The red‑to‑blue height scale’s in meters.. Not as neat as theory, is it?”

“Wow, that’s a mess. Looks like the Moon’s pulling water along the Canada‑Alaska coast okay, and the western Pacific starts to get a dome going. But the water never catches up before the Moon’s gone.”

“Hey, Vinnie, look how the tides just go round and round New Zealand. And what’s that, Hudson Bay, it’s a pinwheel.”

“Yeah, and in between Africa and Madagascar it’s completely out of phase from what it oughta be.”

“What you’re looking at is slosh. Once again, reality overwhelms a pretty theory. Each basin has its own preferred set of oscillations. None of them match up with the Moon. But the other thing — “

“Tiny numbers. Everything’s like less than a couple meters, not not a big bulge at all.”

“Bingo, Vinnie. Against Earth’s 6.4‑million‑meter radius, those small chaotic sloshes don’t make for effective energy transfer driving the Moon away from us. That theory’s toast.”

“So what’s doing it?”

“There’s two theories that I know of, and they’re probably both right. The first one is Earth tides — that bump you think of as traveling around the planet, but the bump is rock instead of water.”

“That can’t be a big effect. Rocks don’t bend.”

“On a planetary scale they’re not as solid as you think, Vinnie. The rock crust is brittle and really thin, less than half a percent of Earth’s radius. It floats on molten outer mantle which has the fluidity of tapioca pudding. When that structure gives under stress the crust layer cracks. The seismologists and GPS techs have measured surface motion all over the world. When they analyze the maps, the lunar component accounts for up to a meter of coordinated vertical daily movement. Figure the whole Earth is continually being squeezed and pulled to that extent and you’ve got a lot of energy being expended every 24 hours.”

“How about the other theory?”

“There’s no direct evidence, so far as I know, but it seems reasonable on physical grounds. We’ve got two gyrations going on here, right? The Moon is on a 29½‑day orbit while the Earth rotates about thirty times faster. But the two motions use different frames. The Earth’s spin axis runs through the geometric center of the planet and tilts 23° from its orbit axis. Meanwhile the whole Earth‑Moon system rotates about its barycenter, their common center of gravity, which stays inside the Earth about ¾ of the way moonward from the Earth’s middle. That rotation is about 5° away from Earth’s orbit’s axis. Imagine a molten blob near the barycenter, happily following the Moon in the Earth-Moon frame, but the rest of the planet is saying, ‘No, no, you’re supposed to be moving hundreds of miles an hour in a different direction!‘ If the blob’s the least bit lighter or heavier than its neighbor blobs, inertial forces expend energy to kick it out of there.”

“So we got two ways to transfer energy steady-like.”

“I think so.”

~~ Rich Olcott

Here’s a Different Angle

On By rolcottIn Astronomy: Planetary Science, Physics: Fundamentals, UncategorizedLeave a comment

“OK, Sy, so there’s a bulge on the Moon’s side of the Earth and the Earth rotates but the bulge doesn’t and that makes the Moon’s orbit just a little bigger and you’ve figured out that the energy it took to lift the Moon raised Earth’s temperature by a gazillionth of a degree, I got all that, but you still haven’t told Al and me how the lifting works.”

“You wouldn’t accept it if I just said, ‘The Moon lifts itself by its bootstraps,’ would you?”

“Not for a minute.”

“And you don’t like equations. <sigh> OK, Al, pass over some of those paper napkins.”

“Aw geez, Sy.”

“You guys asked the question and this’ll take diagrams, Al. Ante up. … Thanks. OK, remember the time Cathleen and I caught Vinnie here at Al’s shop playing with a top?”

“Yeah, and he was spraying paper wads all over the place.”

“I wasn’t either, Al, it was the top sending them out with centri–…, some force I can never remember whether it’s centrifugal or centripetal.”

“Centrifugal, Vinnie, –fugal– like fugitive, outward‑escaping force. It’s one of those ‘depends on how you look at it‘ fictitious forces. From where you were sitting, the wads looked like they were flying outward perpendicular to the top’s circle. From a wad’s point of view, it flew in a straight line tangent to the circle. It’s like we have two languages, Room and Rotor. They describe the same phenomena but from different perspectives.”

“Hey, it’s frames again, ain’t it?”

“Newton’s inertial frames? Sort‑of but not quite. Newton’s First Law only holds in the Room frame — no acceleration, motion is measured by distance, objects at rest stay put. Any other object moves in a straight line unless its momentum is changed by a force. You can tackle a problem by considering momentum and force components along separate X and Y axes. Both X and Y components work the same way — push twice as hard in either direction, get twice the acceleration in that direction. Nice rules that the Rotor frame doesn’t play by.”

“I guess not. The middle’s the only place an object can stay put, right?”

“Exactly, Al. Everything else looks like it’s affected by weird, constantly‑varying forces that’re hard to describe in X‑Y terms.”

“So that breaks Newton’s physics?”

“Of course not. We just have to adapt his F=m·a equation (sorry, Vinnie!) to Rotor conditions. For small movements we wind up with two equations. In the strict radial direction it’s still F=m·a where m is mass like we know it, a is acceleration outward or inward, and F is centrifugal or centripetal, depending. Easy. Perpendicular to ‘radial‘ we’ve got ‘angular.’ Things look different there because in that direction motion’s measured by angle but Newton’s Laws are all about distances — speed is distance per time, acceleration is speed change per time and so forth.”

“So what do you do?”

“Use arc length. Distance along an arc is proportional to the angle, and it’s also proportional to the radius of the arc, so just multiply them together.”

“What, like a 45° bend around a 2-foot radius takes 90 feet? That’s just wrong!”

“No question, Al. You have to measure the angle in the right units. Remember the formula for a circle’s circumference?”

“Sure, it’s 2πr.”

“Which tells you that a full turn’s length is 2π times the radius. We can bridge from angle to arc length using rotational units so that a full turn, 360°, is 2π units. We’ll call that unit a radian. Half a circle is π radians. Your 45° angle in radians is π/4 or about ¾ of a radian. You’d need about (¾)×(2) or 1½ feet of whatever to get 45° along that 2-foot arc. Make sense?”

“Gimme a sec … OK, I’m with you.”

“Great. So if angular distance is radius times angle, then angular momentum which is mass times distance per time becomes mass times radius times angle per time.”

“”Hold on, Sy … so if I double the mass I double the momentum just like always, but if something’s spinning I could also double the angular momentum by doubling the radius or spinning it twice as fast?”

“Couldn’t have put it better myself, Vinnie.”

~~ Rich Olcott