The impromptu seminar at Change-me Charlie’s “Change My Mind” table is still going strong, but it looks like Physicist-in-training Newt and Astronomer-in-training Jim have met his challenge. He’s switched from arguing that dark matter doesn’t exist to asking how it worked in the Bullet Cluster’s massive collision between two collections of galaxies with their clouds of plasma and dark matter. “OK, the individual galaxies are so spread out they slide past each other without slowing down but the plasma clouds obstruct each other by friction. Wouldn’t friction in the dark matter hold things back, too?”
Jim’s still standing in front of the table. “Now that’s an interesting question, so interesting that research groups have burned a bazillion computer cycles trying to answer it.”
“Interesting, yes, but that interesting?”
“For sure. What we know about dark matter is mostly what it doesn’t do. It doesn’t give off light, it doesn’t absorb light, it doesn’t seem to participate in the strong or weak nuclear forces or interact with normal matter by any means other than gravity, and no identifiable dark matter particles have been detected by bleeding-edge experiments like IceCube and the Large Hadron Collider. So people wonder, does dark matter even interact with itself? If we could answer that question one way or the other, that ought to tell us something about what dark matter is.”
“How’re we gonna do that?”
Newt’s still perched on Charlie’s oppo chair. “By using computers and every theory tool on the shelf to run what-if? simulations. From what we can tell, nearly everywhere in the Universe normal matter is embedded in a shell of dark matter. The Bullet Cluster and a few other objects out there appear to break that rule and give us a wonderful check on the theory work.”
“Like for instance.”
“Simple case. What would the collision would looked like if dark matter wasn’t involved? Some researchers built a simulation program and loaded it with a million pretend plasma particles in two cluster-sized regions moving towards each other from 13 million pretend lightyears apart. They also loaded in position and momentum data for the other stars and galaxies shown in the NASA image. The simulation tracked them all as pretend-time marched along stepwise. At each time-step the program applied known or assumed laws of physics to compute every object’s new pretend position and momentum since the prior step. Whenever two pretend-particles entered the same small region of pretend-space, the program calculated a pretend probability for their collision. The program’s output video marked each successful collision with a pink pixel so pinkness means proton-electron plasma. Here’s the video for this simulation.”
“Doesn’t look much like the NASA picture. The gas just spreads out, no arc or cone to the sides.”
“Sure not, which rules out virtually all models that don’t include dark matter. So now the team went to a more complicated model. They added a million dark matter particles that they positioned to match the observed excess gravity distribution. Those’re marked with blue pixels in the videos. Dark matter particles in the model were allowed to scatter each other, too, under control of a self-interaction parameter. The researchers ran the simulations with a whole range of parameter values, from no-friction zero up to about twice what other studies have estimated. Here’s the too-much case.”
“Things hold together better with all that additional gravity, but it’s not a good match either.”
“Right, and here’s the other end of the range — no friction between dark matter particles. Robertson, the video’s author/director, paused the simulation in the middle to insert NASA’s original image so we could compare.”
“Now we’re getting somewhere.”
“It’s not a perfect match. Here’s an image I created by subtracting a just-after-impact simulation frame from the NASA image, then amplifying the red. There’s too much left-over plasma at the outskirts, suggesting that maybe no-friction overstates the case and maybe dark matter particles interact, very slightly, beyond what a pure-gravity theory predicts.”
“Wait, if the particles don’t use gravity, electromagnetism or the nuclear forces on each other, maybe there’s a fifth force!”
“New Physics!”
A roar from Cap’n Mike — “Or they’re not particles!”
~~ Rich Olcott
“So you’re telling me, Cathleen, that you can tell how hot a star is by 
Cathleen turns to her laptop and starts tapping keys. “Let’s do an example. Suppose we’re looking at a star’s broadband spectrogram. The blackbody curve peaks at 720 picometers. There’s an absorption doublet with just the right relative intensity profile in the near infra-red at 1,060,190 and 1,061,265 picometers. They’re 1,075 picometers apart. In the lab, the sodium doublet’s split by 597 picometers. If the star’s absorption peaks are indeed the sodium doublet then the spectrum has been stretched by a factor of 1075/597=1.80. Working backward, in the star’s frame its blackbody peak must be at 720/1.80=400 picometers, which corresponds to a temperature of about 6,500 K.”
“That’s not quite what I said, Jennie. Old Reliable’s software and and I worked up a hollow-shell model and to my surprise it’s consistent with one of Stephen Hawking’s results. That’s a long way from saying that’s what a black hole is.”
My notes say D is the black hole’s diameter and d is another object’s distance from its center. One second in the falling object’s frame would look like f seconds to us. But one mile would look like 1/f miles. The event horizon is where d equals the half-diameter and f goes infinite. The formula only works where the object stays outside the horizon.”
“Wow, Old Reliable looks up stuff and takes care of unit conversions automatically?”
, where D is the object’s diameter and d is your distance from it. Suppose the Sun suddenly collapsed without losing any mass to become a Schwarzchild object. The object’s diameter would be a bit less than 4 miles. Earth is 93 million miles from the Sun so the compression factor here would be [poking numbers into my smartphone] 1.000_000_04. Nothing you’d notice. It’d be 1.000_000_10 at Mercury. You wouldn’t see even 1% compression until you got as close as 378 miles, 10% only inside of 43 miles. Fifty percent of the effect shows up in the last 13 miles. The edge of a black hole is sharper than this pizza knife.”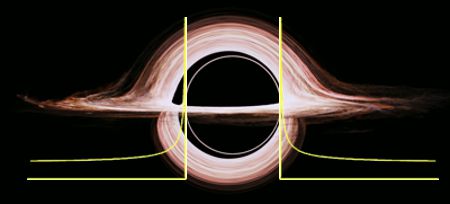
. A is proportional to spin. When A is small (not much spin) or the distance is large those A/d² terms essentially vanish relative to the others and the scaling looks just like the simple almost-a-point Schwarzchild case. When A is large or the distance is small the A/d² terms dominate top and bottom, the factor equals 1 and there’s dragging but no compression. In the middle, things get interesting and that’s where Dr Thorne played.”
Hard Science Ain't Hard 